Misceláneas: Probabilidad. Inferencia.
Misceláneas: Probabilidad. Inferencia.
Geometría y Probabilidad.
En los diferentes subproyectos que conforman la organización no gubernamental RED Descartes hay profusión de contenidos relativos a la Estadística y la Probabilidad que prácticamente cubren las exigencias curriculares de Primaria, ESO y Bachillerato. La particularidad de estos contenidos es que son: dinámicos, interactivos, formativos y en algunos casos, además, evaluativos. Ya en la anterior entrada en este blog señalamos algunos de esos recursos y siguiendo en esa línea y teniendo en cuenta que nuestro objetivo es el análisis de los errores de tipo I y II en los contrastes (tests) de hipótesis hemos seleccionado los siguientes contenidos:
- La Unidad Didáctica "El azar y la probabilidad." de la profesora Ángela Nuñez Castaín (2001) posteriormente adaptada a DescartesJS por ella misma y José R. Galo Sánchez (2017). La unidad es un primer acercamiento a los conceptos del azar y la probabilidad mediante ejemplos interactivos elementales ideales para conocer/recordar los fundamentos teóricos del estudio del azar.
- Si ya se conocen los fundamentos básicos de la Estadística y la Probabilidad el libro digital "Estadística, Combinatoria y Probabilidad" de Juan Jesús Cañas Escamilla y José R. Galo Sánchez, es la siguiente fuente de donde extraer la consolidación teórica rigurosa de los principios elementales y la justificación de los procesos operativos relacionados con los cálculos probabilísticos además de las técnicas organizativas de la información numérica en tablas y gráficos. Todo ello de forma gradual y apoyado en multitud de escenas interactivas de alto nivel educativo.
- En tercer lugar enlazamos el extraordinario libro digital interactivo "Estadística, Probabilidad e Inferencia", también de los autores Juan Jesús Cañas Escamilla y José R. Galo Sánchez, que hace un completo recorrido por los conceptos relativos a: la Estadística Unidimensional, Bidimensional, la Combinatoria, la Probabilidad, las variables estadísticas discretas y continuas y sus respectivas distribuciones de probabilidad y termina con un espléndido y documentadísimo análisis de la teoría del muestreo probabilístico y la inferencia estadística, todo ello acompañado de una batería de ejemplos, escenas interactivas, vídeos relativos a los contenidos y enlaces que hacen que el nivel de profundización en el estudio de la materia quede en manos de la persona interesada. Un ejemplo de escena interactiva, de las muchas que contiene el libro, es el que mostramos a continuación que apoya los conceptos teóricos de la introducción al estudio de los Intervalos de Confianza.
También enlazamos la excelente unidad didáctica, dinámica e interactiva, creada con DescartesJS por la profesora Mª José García Cebrian (2001) y revisada y adaptada por ella misma (2017) INFERENCIA ESTADÍSTICA
El problema de la aguja de Buffon - Laplace
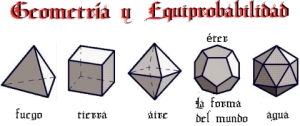
Desde la generalización del uso del astrágalo (taba) para dilucidar todo tipo de cuestiones relacionadas con la incertidumbre o sencillamente como elemento lúdico para ejercitar la habilidad mezclada con la suerte, la Geometría y el Azar comenzaron a ir de la mano. De hecho el gráfico de los cuerpos platónicos que mostramos en la cabecera de esta entrada es probablemente una de las mejores definiciones de equiprobabilidad que podamos ver. El hecho tangible de manipular cualquiera de estos cuerpos transmite una sensación de equilibrio, perfección y equidad, amén de otras, difícilmente igualable.
Los motivos por los que, primero el conde de Buffon y más tarde Pierre-Simón Laplace, conde del Imperio, atendieron este problema no están claros. El efecto inmediato si, a partir de entonces la utilidad del uso de la Geometría en cuestiones de probabilidad estaba comprobada así como el uso de métodos estadísticos y probabilísticos para aproximar valores de constantes geométricas.
Con el objetivo de rememorar el establecimiento formal de la relación entre la Estadística-Probabilidad con la Geometría y también por la idoneidad del experimento con la introducción al estudio de la Inferencia Estadística que estamos desarrollando se ha elaborado la miscelánea "Experimento: La Aguja de Buffon". En esta miscelánea se recrea dicho experimento con las siguientes particularidades:
- La escena simula el lanzamiento de 2 a 30000 agujas (o el lanzamiento de una aguja de 2 a 30000 veces).
- Cada lanzamiento de k agujas puede repetirse n veces así puede analizarse, en cada muestra, el comportamiento de los estadísticos estudiados, la influencia del tamaño de las muestras en el comportamiento de los estadísticos, el cumplimiento de la ley de los grandes números y otros.
- Si el número de lanzamientos es menor o igual a 500 se representa cada una de las agujas lanzadas; si el número de agujas es mayor se muestra únicamente el punto medio de cada aguja.
- Con cada lanzamiento la escena expone un breve resumen de los resultados, así como el valor aproximado de π y la probabilidad de tocar línea en la muestra.
- El botón Indicaciones explica los objetivos y funcionalidad de la miscelánea.
- La escena posibilita que en pocos minutos puedan realizarse experimentos como el que muestra el siguiente documento.

Experimento de Buffon. Lanzamiento de agujas.
En esta ocasión, en la sección de vídeo, hemos elegido uno que muestra una clase sobre la estimación de la media poblacional mediante intervalos de confianza. Este vídeo es uno de los enlazados en el libro digital interactivo "Estadística, Probabilidad e Inferencia".
Acerca de los cuerpos platónicos.
- MATEMÁTICA Y FÍSICA EN EL TIMEO DE PLATÓN. POLIEDROS REGULARES Y ELEMENTOS NATURALES
- Los poliedros regulares y la esfera de: Javier Abia Llera (Adaptación a DescartesJS: José R. Galo Sánchez)
- *"El dodecaedro es la forma que los dioses emplean para disponer las constelaciones en los cielos." Platón
Ildefonso Fernández Trujillo. 2018
Misceláneas. Probabilidad a posteriori. Teorema de Bayes.
Misceláneas. Probabilidad a posteriori. Teorema de Bayes.
Ley de los grandes números
En la Wikipedia, al buscar información sobre el tema, encontramos lo siguiente:
"En la teoría de la probabilidad, bajo el término genérico de ley de los grandes números se engloban varios teoremas que describen el comportamiento del promedio de una sucesión de variables aleatorias conforme aumenta su número de ensayos.
Estos teoremas prescriben condiciones suficientes para garantizar que dicho promedio converge (en los sentidos explicados abajo) al promedio de las esperanzas de las variables aleatorias involucradas. Las distintas formulaciones de la ley de los grandes números (y sus condiciones asociadas) especifican la convergencia de formas distintas.
Las leyes de los grandes números explican por qué el promedio de una muestra al azar de una población de gran tamaño tenderá a estar cerca de la media de la población completa.
Cuando las variables aleatorias tienen una varianza finita, el teorema central del límite extiende nuestro entendimiento de la convergencia de su promedio describiendo la distribución de diferencias estandarizadas entre la suma de variables aleatorias y el valor esperado de esta suma: sin importar la distribución subyacente de las variables aleatorias, esta diferencia estandarizada converge a una variable aleatoria normal estándar.
La frase "ley de los grandes números" es también usada ocasionalmente para referirse al principio de que la probabilidad de que cualquier evento posible (incluso uno improbable) ocurra al menos una vez en una serie aumenta con el número de eventos en la serie. Por ejemplo, la probabilidad de que un individuo gane la lotería es bastante baja; sin embargo, la probabilidad de que alguien gane la lotería es bastante alta, suponiendo que suficientes personas comprasen boletos de lotería.
El matemático italiano Gerolamo Cardano (1501–1576) afirmó sin pruebas que la precisión de las estadísticas empíricas tienden a mejorar con el número de intentos. Después esto fue formalizado como una ley de los grandes números. Una forma especial de la ley (para una variable aleatoria binaria) fue demostrada por primera vez por Jacob Bernoulli. Le llevó más de 20 años desarrollar una prueba matemática..."
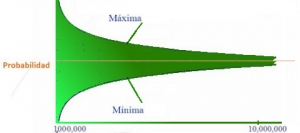
La siguiente imagen enlaza con una pequeña utilidad dados.xls creada con Microsoft Excell 2010 que simula el lanzamiento de un dado y comprueba lo predicho. La hoja de cálculo, que es editable, simula el lanzamiento de un dado desde 90.000 a 63.000.000 de veces. Cada 'lanzamiento' consiste en generar, de forma 'aleatoria' (semialeatoria), un número entero del 1 al 6, y tener en cuenta el resultado incrementando en una unidad la cantidad apropiada. Se observa como al realizar pruebas sucesivas aumentando en cada una el número de lanzamientos el valor de la frecuencia relativa de un suceso concreto va acercándose muy lentamente al valor teórico previsto para su probabilidad de ocurrencia.
Aquí tocamos un tema interesante, la generación de números aleatorios (semialeatorios). Cada lenguaje de programación, cada intérprete y cada autor tiene su propia manera de generar números aleatorios. El hipervínculo anterior es un ejemplo de lo dicho y al final del artículo se enlazan algunas de las páginas que tratan este asunto.
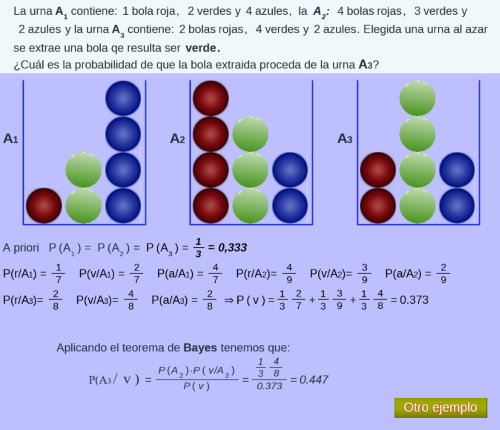
El Teorema de Bayes
Dentro de la particularidad que nos ocupa: el estudio de la probabilidad a posteriori, o también probabilidad de las causas, que evidentemente es consecuencia de lo comentado en los párrafos anteriores, destaca la labor de Thomas Bayes que con su teorema sobre la probabilidad de las causas condicionadas a los efectos observados, abrió un amplio abanico de posibilidades al estudio científico de múltiples situaciones. El avance de las ciencias sociales, políticas y económicas, por citar algunas, se debe al uso acertado y sistemático de esta filosofía, además de a otras herramientas afines.

donde:
- {A1, A2, A3,....., An} es un sistema completo de sucesos y se conocen las probabilidades P(Ai) (probabilidades a priori).
- B es un suceso cualquiera y P(B/Ai) es conocida, por lo tanto también se conoce P(B).
- P(Ai/B) es la probabilidad a posteriori a calcular.
A continuación enlazamos con una utilidad, creada con el editor DescartesJS, en la que, en primer lugar, se plantea una situación resoluble mediante el teorema de Bayes. Siguiendo las indicaciones que proporciona la propia escena, esta muestra el planteamiento y solución del ejercicio y más adelante la utilidad plantea, en una nueva escena, otra situación similar para que la persona interesada la resuelva ofreciéndose la posibilidad de contrastar la solución.
Entre los materiales disponibles para su uso y descarga en la web de la Red Descartes, relacionados con la Estadística y la Probabilidad, se encuentra una completa colección de utilidades que cubren todo el recorrido curricular, desde Primaria a Bachillerato. La autoría de estos materiales corresponde a miembros de la Red Descartes y, entre otros, destacamos la labor de:
- Juan Guillermo Rivera Berrío. Juego del Gato y el Ratón.
- Diego Luis Feria Gómez. Probabilidad.
- José Ireno Fernández Rubio / María José García Cebrian / Consolación Ruiz Gil. Estadística.
En próximas entradas continuaremos exponiendo enlaces a algunos de los contenidos interactivos de Estadística y Probabilidad significativos por su capacidad didáctica.
En esta ocasión, en la sección de vídeo, hemos elegido uno que muestra la aplicación del teorema de Bayes a la resolución de un problema.
A continuación exponemos algunos enlaces a la información sobre la generación de números aleatorios.
- Wikipedia
- Números aleatorios II
- Números aleatorios III por Manuel A. Pulido Cayuela
- Números aleatorios IV
- Números aleatorios V
Ildefonso Fernández Trujillo. 2018
La Probabilidad Total. Ejercicios.
Misceláneas. La probabilidad total.
A las cuentas del estado tradicionalmente se les ha llamado estadísticas y habitualmente estas cuentas se han dado a conocer por parte de los sucesivos gobiernos de forma periódica. En la actualidad el diccionario define la estadística como: Ciencia que utiliza conjuntos de datos numéricos para obtener, a partir de ellos, inferencias basadas en el cálculo de probabilidades. En la wikipedia encontramos: "La estadística (la forma femenina del término alemán Statistik, derivado a su vez del italiano statista, "hombre de Estado") es una rama de las matemáticas y una herramienta que estudia usos y análisis provenientes de una muestra representativa de datos, que busca explicar las correlaciones y dependencias de un fenómeno físico o natural, de ocurrencia en forma aleatoria o condicional...."
Dentro de la particularidad que nos ocupa: la probabilidad total, también hemos de tener en cuenta el juego ya que diferentes artistas y científicos interesados en el azar lo han tomado como referencia para elaborar obras y contenidos de indudable valor. En este sentido mostramos a continuación la imagen de una ruleta donde se recomienda el estudio de la situación de los números en la misma.
La imagen anterior enlaza con uno de los blogs del escritor, bloguero y divulgador "freelance" (por libre) Alfred López sobre curiosidades generales, donde muestra una breve pero selecta información relacionada con el tema de la probabilidad y la ruleta. (En este enlace se expone la procedencia de las imágenes que se usan)
En la imagen siguiente puede verse el mantel (que incorpora el cero) de la mesa de juego de la ruleta, lo que nos permite seguir la exposición enlazada anteriormente.
En la Wikipedia podemos documentarnos, de manera concisa y precisa, sobre el azar
Enlazamos, a continuación con el esmerado trabajo JUGANDO CON LA PROBABILIDAD, elaborado por un grupo de profesores de la Universidad de Granada.
Lo dicho anteriormente y la propia experiencia nos lleva al objetivo principal de esta entrada, un intento de análisis del alma del azar, la incertidumbre. Cuando, a relativamente temprana edad, nos enfrentamos formalmente con la resolución de situaciones donde interviene el azar, ya llevamos un bagaje de conocimientos adquiridos naturalmente a través de los juegos en familia o con las amistades, es decir, ya conocemos la incertidumbre. Pero este conocimiento, lejos de ayudar, en principio parece ser perjudicial, ya que automáticamente la intuición prevé que la solución de una situación donde interviene el azar es inútil ya que fácticamente y de forma inmediata no tiene ningún sentido tangible, es imposible de constatar fácticamente. Más adelante cuando aceptamos la utilidad del conocimiento de la tendencia de un suceso y es más, cuando la realidad nos muestra como una probabilidad se convierte en un hecho fáctico previsto gracias a un buen estudio previo basado en el azar es cuando percibimos la importancia fundamental del conocimiento de las herramientas estadísticas y su utilización. Como introducción a ese estudio y suponiendo que la persona que accede a este artículo ya posee una base elemental de los fundamentos estadísticos y de probabilidad, hemos elaborado la siguiente utilidad donde se analizan y resuelven situaciones relacionadas con la probabilidad total de un suceso.
En esta ocasión, en la sección de vídeo, hemos elegido uno que muestra, en francés, la introducción al teorema de Bayes.
Animamos a colaborar elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo. 2018
Subproyecto GEOgráfica
Subproyecto GEOgráfica.
Cuando en 1970 el futurólogo Alvin Toffler, estudioso de la revolución digital, la revolución de las comunicaciones y la singularidad tecnológica, avanzó en su libro "El shock del futuro" una descripción de la realidad actual acertó en un porcentaje increíblemente alto. Creo recordar que el fenómeno del desplazamiento social masivo y continuo, por motivos lúdicos o de otra índole, no fue previsto en su dimensión real. En aquellos años el término low cost aún no existía; aunque ya empezaba a tomar forma su predecesor, vuelo chárter. Es preciso reconocer que los conceptos anteriores: low cost, revolución digital, revolución de las comunicaciones y la evolución tecnológica han creado una nueva realidad social.
Con objeto de "estar al día" socialmente, varios miembros de la Red Descartes y otros compañeros del ámbito educativo notaron que a raíz de que los términos asociados a los desplazamientos: Latitud, Longitud y Altitud comenzaban a tomar una significación relevante en la vida cotidiana debido a su intervención en todo lo relacionado con la localización de lugares en un mapa, que más adelante, con la aparición de los planos y mapas digitales, incrementó su significación de manera exponencial, decíamos que un grupo de profesores vio que era preciso crear medios para familiarizar al alumnado con dichos términos y con la nueva realidad social. Esto hizo que en el año 2014 varios miembros de la Red Descartes, tanto de España como de Colombia y México, crearan una serie de objetos didácticos, interactivos, lúdicos y con capacidad de evaluar en tiempo real el nivel de conocimientos sobre los países, sus capitales, ríos, monumentos, cultura etc. de la persona que hace uso del objeto didáctico, así nació el subproyecto GEOgráfica.
Recomendamos la lectura completa del Inicio, Introducción y Manual de usuario de la página enlazada con la imagen anterior antes de comenzar a usar los materiales del proyecto.
Desde un principio los miembros de la Red Descartes de Colombia, con su aluvión de excelentes creaciones y extraordinarias ideas tomaron las riendas de la evolución del proyecto al que fueron dando forma. En primer lugar este se desglosó en cuatro apartados:
Sin desmerecer el esfuerzo y aciertos de todos y cada uno de los miembros de la Red Descartes que han intervenido en el desarrollo del proyecto GEOgráfica debemos destacar la profunda visión y acierto de la propuesta del profesor Diego Luis Feria Gómez al incluir, en el año 2016, en el apartado GEOcapital, cinco extraordinarios trabajos sobre la geolocalización de las capitales de los cinco continentes mediante el uso, en tiempo real, de mapas de Google.



Geolocalización de las capitales de África, América y Asia.


Geolocalización de las capitales de Europa y Oceanía
La propuesta que en boca del autor de este artículo y del profesor Ángel Cabezudo Bueno en su plantilla para la utilidad dicen:"...La Geolocalización de Capitales es una actividad que podemos encontrar en la sección GEOcapital del subproyecto GEOgráfica desarrollado por la "Red Educativa Digital Descartes" proyectodescartes.org En este contexto entendemos por geolocalización de la capital de un determinado país, estado o territorio como la consulta de su ubicación sobre un mapa y cuyo posicionamiento se obtiene a través de sus coordenadas geográficas -latitud y longitud-
La actividad pretende que con la práctica el usuario pueda probar su capacidad de localización en un mapa de Google de las capitales de un determinado territorio del mundo. El objeto interactivo solicita al usuario que señale sobre el mapa el marcador de localización ![]() donde hay que situar la capital de un determinado país, dado aleatoriamente, dentro del conjunto de países registrados. La reiteración de este ejercicio con la ayuda ofrecida y las marcas de latitud y longitud que se dibujan en el mapa facilitan la memorización de estas capitales. No hay que insistir mucho para justificar el interés que hoy en día tiene poder traer enseguida a la memoria este tipo de datos y disponer de una referencia mental de la situación de un determinado país o capital correspondiente frente a las noticias que nos llegan desde diferentes medios de información (prensa, radio, televisión, etc.)..."
donde hay que situar la capital de un determinado país, dado aleatoriamente, dentro del conjunto de países registrados. La reiteración de este ejercicio con la ayuda ofrecida y las marcas de latitud y longitud que se dibujan en el mapa facilitan la memorización de estas capitales. No hay que insistir mucho para justificar el interés que hoy en día tiene poder traer enseguida a la memoria este tipo de datos y disponer de una referencia mental de la situación de un determinado país o capital correspondiente frente a las noticias que nos llegan desde diferentes medios de información (prensa, radio, televisión, etc.)..."
Es inmediata la consecuencia de ampliar la idea de geolocalización a las capitales de las provincias, países o territorios de cualquier nación, fundamentalmente; aunque no de forma exclusiva, de las naciones más grandes, como son: India, Estados Unidos, China y Rusia. De hecho en la actualidad ya existen dos nuevos trabajos, uno sobre la geolocalización de las capitales de los territorios y países de la India y otro sobre las capitales de los estados de los Estados Unidos de América del Norte, que enlazamos a continuación, estando la creación del resto en preparación o a disposición de quien decida implementar algún dearrollo.


Geolocalización de las capitales de la India y Estados Unidos
También, consecuentemente, sería conveniente la creación de utilidades interactivas de geolocalización de monumentos, museos, edificios emblemáticos, lugares más visitados, restaurantes, cines, teatros etc. de las capitales más grandes y relevantes, o cualquier otra de interés, con objeto de facilitar la movilidad y aprovechar las breves estancias en ellas.
Así mismo existen varias propuestas de ampliación del proyecto GEOgráfica con los apartados de: GEOríos, GEOmontañas, GEOcultura etc. con la intención de convertir el proyecto en un instrumento eficaz para difundir, a un nivel básico, los conocimientos elementales que en la actualidad constituyen, en el área que trata, los requisitos mínimos necesarios para ser considerado como una persona "alfabetizada".
En esta ocasión, en la sección de vídeo, hemos elegido uno que muestra la deducción, paso a paso, de la geolocalización de un lugar.
Animamos a colaborar elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo. 2018
Subproyecto Misceláneas
Subproyecto Misceláneas.
El subproyecto Misceláneas está de enhorabuena, que se recuerde, pocas veces, en tan poco tiempo, un grupo tan reducido de personas ha aportado tanta cantidad de objetos de tan elevada calidad y tan alto potencial educativo a cualquiera de los subproyectos de la Red Descartes. Y no es la intención desmerecer al resto, muy al contrario; si no la de dar merecida notificación de un hito tan memorable. La excepcionalidad se justifica a si misma nada más visualizar cualesquiera de las últimas escenas incorporadas al subproyecto, lo que ya ha sido posible gracias a las reseñas que tanto José R. Galo Sánchez como Ángel Cabezudo Bueno han expuesto recientemente en el apartado Últimos materiales del blog y al artículo que el primero de ellos acaba de publicar, también en este blog, donde justifica el proceso de creación, creando a su vez nuevas escenas relacionadas con el tema de proporcionar una ayuda inestimable a la capacidad de visualización de las transformaciones dinámicas en el espacio tridimensional. Por otro lado la buena salud del subproyecto también se debe a la infatigable tarea de adaptación de materiales obsoletos, al nuevo editor DescartesJS, de las profesoras Elena E. Álvarez Sáiz y María José García Cebrian, los profesores ya mencionados y otros/as que aunque no se indican están en la mente de todos los usuarios del portal. Relativo a las aportaciones más recientes caben destacar:
- De la profesora Rita Jiménez Igea, quien nos ha sorprendido con un nuevo diseño de las escenas, más funcional, interactivo, armonioso y desde luego con un potencial instructivo y didáctico encomiable, seleccionamos una muestra de sus aportaciones:
De las que destacamos:


Matemáticas, joyería y mezclas.
- Seleccionar parte de las aportaciones del profesor José R. Galo Sánchez al subproyecto Misceláneas o casi a cualquier otro subproyecto es una tarea ardua, así que seleccionaré cronológicamente las siete últimas aportaciones relacionadas con el desarrollo del cubo y de entre ellas destacaré las tres más recientes; no obstante quisiera aprovechar la ocasión para documentar la génesis de la creación de las siete últimas y extraordinarias aportaciones de nuestro presidente para dar valor al ejercicio de la colaboración entre socios a tenor de los frutos obtenidos.
En el año 2001 la profesora Ángela Nuñez Castaín publicó la miscelánea Partición de un cubo en seis pirámides triangulares iguales, en el año 2017 se adaptó a DescartesJS dicha miscelánea, la adaptación fué realizada conjuntamente por la profesora y nuestro presidente. A continuación se muestra el resultado obtenido. Las misceláneas más recientes que se han publicado sobre el tema han sido:- Partición de un cubo en pirámides de base cuadrada. Caso general.
- Partición de un cubo en 4 pirámides cuadradas iguales dos a dos
- Partición de un cubo en seis pirámides triangulares congruentes
- Partición de un cubo en cinco pirámides triangulares
- Partición de un cubo en seis pirámides cuadradas iguales
- Partición de un cubo en cinco pirámides cuadradas
- Partición de un cubo en tres pirámides cuadradas iguales
- A la hora de cerrar este artículo nos vemos sorprendidos por una nueva y brillante aportación del profesor José R. Galo Sánchez que aunque aún no hemos tenido tiempo de analizar en profundidad consideramos de interés prioritario su exposición. Partición no prismática de un cubo en seis pirámides triangulares equivalentes
De las anteriores destacamos:
- A continuación, también a modo de resumen, exponemos tres misceláneas: la primera, que muestra la cuadratura de un polígono regular, elaborada por el profesor Ángel Cabezudo Bueno y el autor de este artículo y las otras dos, de este último, relativas a los patrones de teselación tipo mitad del cuadrado.
- Pentágono regular: Cuadratura. Método clásico
- Teselas del plano. Patrones: Mitad del cuadrado
- Teselas del plano. Patrones: Mitad del cuadrado II
En esta ocasión, en la sección de vídeo, hemos elegido uno que muestra una presentación de los cuerpos platónicos diferente a lo habitual.
Ildefonso Fernández Trujillo. 2018