PRISMAS Y PIRÁMIDES

José Ireno Fernández Rubio

Fondo Editorial RED Descartes

Título:
PRISMAS Y PIRÁMIDES

Autor:
Jose Ireno Fernández Rubio

Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS, WebSim, Phet Colorado, GeoGebra, ...
Fuentes: Lato y UbuntuMono
Imagen de portada: ilustración generada por Chatgpt y modificada por Ireno

Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org

Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm

ISBN: 978-84-10368-44-6

Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.

Imagen creada con Grok

Previo 1

Consideraciones en torno a las unidades.

No he empleado el uso de unidades $(cm, cm^2, cm^3 , m, m^2, m^3,...)$ a lo largo del libro, ni siquiera la nomenclatura $u, u^2$ y $ u^3$. Y sin embargo sí se toman medidas de longitud y se hacen cálculos de áreas y volúmenes. Siempre se deberá entender $u, u^2$ y $u^3$ para cualquier medida de longitud, superficie y volumen respectivamente. Y si queremos que sean en cm, serán $cm, cm^2$ y/o $cm^3$; pero si queremos que sean m serán $m, m^2 $ y/o $ m^3$ según sea de longitud, supeficie o volumen. Podemos emplear cualquier unidad, pero siempre la misma y diferenciando entre 1, 2 ó 3 dimensiones

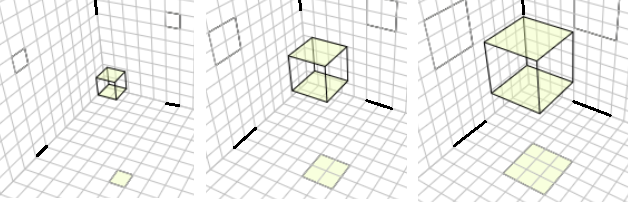
En la parte superior podemos ver unidades de longitud, superficie y volumen en las tres imágenes.

En la central, por ejemplo, podemos observar segmentos de longitud 2, cuadrados de superficie 4 y un cubo de volumen 8.

El la última segmentos de longitud 3, cuadrados de superficie 9 y un cubo de volumen 27

Previo 2

Indicaciones.

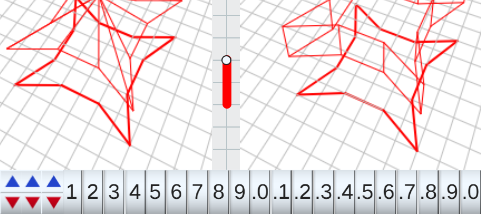
En la mayoría de las escenas aparecen estos controles:

• Un control gráfico central con el que poder elegir la altura de la figura. Puede haber un segundo control central para la altura de la base.
• Tres controles para mover la figura en las tres direcciones del espacio.
• Controles numerados (1, 2, 3, 4...) uno para cada uno de los ejemplos.
• En algunas escenas hay un control para poner/quitar el fondo cuadriculado o las proyecciones en los espacios 3D.

Hay escenas con otros controles pero tienen indicaciones propias. En muchas figuras podemos cambiarle la forma con controles gráficos, trasteando la escena se comprende mejor.

Tabla de contenido

Imagen creada con Grok

INTRODUCCIÓN

Introducción

Las representaciones en Geometría han sido, por si solas, un núcleo central de interés. Las representaciones gráficas, planas o espaciales, tienen una larga tradición y prestigio, habiéndose de distinguir las representaciones al servicio del propio razonamiento geométrico de las representaciones que gracias a la Geometría posibilitan hacer mapas, planos y diseños.

Objetivos

1. Desarrollar la visión espacial.
2. Desarrollar la creatividad.
3. Comprender mejor el concepto de volumen.
4. Construir figuras en 3D y visualizarlas desde distintas perspectivas.
5. Hacer los cálculos correspondientes.

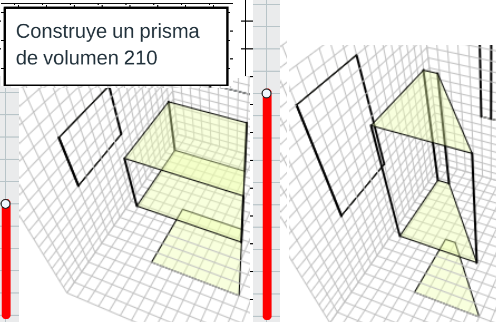
En este libro se le pide al alumno construir además de saber hacer los cálculos. Es algo que en la vida real ocurre, en una fábrica puede necesitarse un depósito de agua, o de líquidos en general con una determinado volumen.

Un problema típico de cálculo de volúmenes.

Un prima tiene de base un trapecio de medidas B=5, b=3 y h=4. Si la altura del prima es 6 calcula su volumen (he omitido las unidades que bien podrían ser cm o m o culaquier otra como indico al principo)

Y aquí puede hacerse un problema que no puede venir en libros de papel como :

Construye un prisma de base un trapecio con un volumen de 210.

En este problema el alumno tiene que construir la figura, y no hay una sóla figura que cumpla el requisito de 210, hay muchas válidas (En la imagen de la izquierda pueden verse dos)

Tambien se le puede pedir que construya varias figuras diferentes con el mismo volumen.

Capítulos adicionales.

1. El capítulo 6 está dedicado al cálculo de áreas
2. En el capítulo 4 vienen unas escenas para comprender mejor el principio de Cavalieri y porqué el volumen de una pirámide es 1/3 del prisma que tiene las mismas dimensiones.
3. En el capítulo 7 vienen 6 constructores generales de figuras. Estos son diferentes a los otros que aparecen en otros capítulos que son específicos para solucionar los problemas propuestos.

Reconocimiento.

Los Primas y las Pirámides los tenemos presentes en muchas cosas y pueden pasar desapercibidas.

Diferencias

Un prisma puede tener la misma altura y la misma base que una pirámide.
A partir de cualquier polígono podemos crear un prisma y una pirámide con igual base y altura. Observa los ejemplos de abajo (pulsa en 1, 2, 3, ...)

Ejercicio

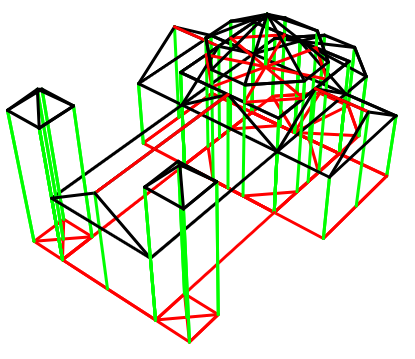
En el dibujo de la derecha aparecen muchos prismas y algunas pirámides. Reconoce al menos 3 de cada. Puedes ayudarte, para descubrirlas todas, de la primera escena, al principio del capítulo. (Solución)

Ejercicio

La imagen simula una ciudad a base de prismas que hacen de edificios. Corresponde con el ejemplo 3 de la escena siguiente.

En la escena puedes cambiar el número de prismas y pirámides, la separación entre los elementos y la escala. Captura 3 imágenes con elementos, número, separacón y escala distintos y recógelas en un documento para enviárselo a tu profesor.

Ejercicio de reconocimiento de prismas.

Ejercicio de reconocimiento de pirámides.

Imagen creada con Grok

PRISMAS

Con base un rectángulo

Con la siguiente escena puedes construir una gran variedad de prismas. Resuelve el ejercicio propuesto. En esta unidad se abordan lo cuerpos geométricos con una regla para medir y luego calcular. Poliedros

Con base un trapecio

Resuelve el ejercicio propuesto.

Con base un triángulo

Resuelve el ejercicio propuesto.

Con base un rombo

Resuelve el ejercicio propuesto.

Con base un paralelogramo

Resuelve el ejercicio propuesto.

Con base variada

Calcula el volumen de varios prismas. Procura que al menos sean tres y que no coincidan en altura.

Ejercicio

Calcula el volumen de tres de las figuras compuestas siguientes (tres del 1 al 14). Varía la altura de los prismas pegados al cubo en los tres casos. Haz capturas de pantalla y escribe los pasos en los tres casos. Manda el archivo a tu profesor.

Ejercicio resuelto.

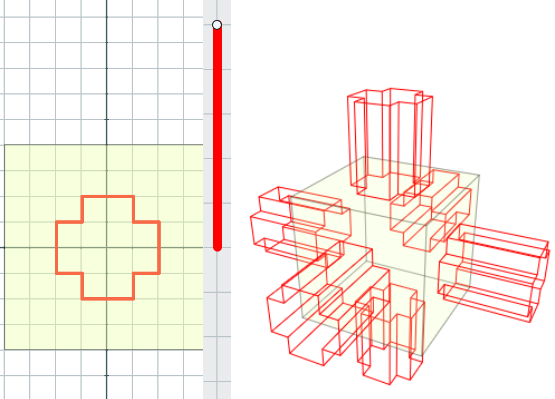
Solución:
Sobre un cubo de arista 8 se han adosado 6 prismas iguales. Cada uno de los 6 prismas tiene base 12 y altura 5.
El volumen será V = 8^3+6·(12·5) = 872.

Imagen creada con Grok

PIRÁMIDES

Con base un rectángulo

Resuelve el ejercicio propuesto.

Con base un trapecio

Resuelve el ejercicio propuesto.

Con base un triángulo

Resuelve el ejercicio propuesto.

Con base un rombo

Resuelve el ejercicio propuesto.

Con base un paralelogramo

Resuelve el ejercicio propuesto.
Intenta construir otra distinta con el mismo volumen (recomiendo descomponer en factores primos el volumen y ayudarse con los factores). Esto también lo puedes hacer con base un rectángulo, trapecio, rombo y triángulo

Con base variada

Calcula al menos tres volúmenes de las 14 figuras posibles. Asigna a estas alturas distintas, por ejemplo 3, 4 y 5

Tronco pirámide

Observa el ejercicio resuelto de la seguiente página y después construye un tronco de pirámide a tu gusto para calcularle el volumen siguiendo los pasos del ejemplo.

Ejercicio

En la parte inferior tienes un ejercicio resuelto. Resuelve 3 diferentes (El volumen de 3 figuras del 1 al 14) y elige diferentes alturas para cada uno.

Ejercicio resuelto.

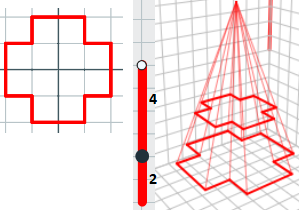
El área de la base inferior es 12. Si consideramos las dos pirámides semejantes, una de altura 4 y otra de altura 6, las razones de semejanza son 4/6 ó 6/4 según se mire. El área de la inferior será $12·(4/6)^2 = 5.333$.
El volumen del tronco será la diferencia de volúmenes entre las dos pirámides, es decir V = 24 - 7.111 = 16.888

Ejercicio

Calcula el volumen de tres de las figuras compuestas siguientes. Varía la altura de los prismas pegados al cubo en los tres casos. Haz capturas de pantalla y escribe los pasos en los tres casos. Manda el archivo a tu profesor.

Ejercicio resuelto.

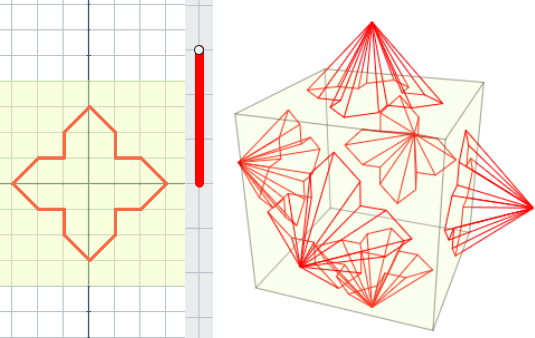
Solución:
Sobre un cubo de arista 8 se han adosado 6 piramides iguales. Cada una de las 6 pirámides tiene base 16 y altura 3.
El volumen será V = 8^3+6·(16·3/3) = 608.

Imagen creada con Grok

PORQUÉS

La inclinación no varía el volumen

Los volúmenes de las dos figuras de la izquierda (el amarillo y el transparente) son iguales y son iguales al de la derecha. A esto se le conoce como el Principio de Cavalieri

Con muchas partes se aproximan mucho

El volumen de las dos pirámides escalonadas (la amarilla y la transparente de la izquierda) no varía por cambiar las n cajas de posicion. Si aumentamos el número n de cajas esos dos volúmenjes siguen siendo iguales pero cada vez difieren menos del volumen de la pirámide de la derecha. Con muchísimas partes son o casi son iguales.

Volumen un tercio del prisma

En la figura vemos un prisma dividido en tres pirámides. La roja y la azul tienen el mismo volumen, son simétricas. Si separamos las figuras podemos apreciar que la azul y la verde comparten base y también tienen la misma altura. Por tanto todas las pirámides tienen igual volumen y será un tercio del volumen del prisma.

Puzle de arrastre.

Imagen creada con Grok

SUMANDO Y
RESTANDO

Sumando

Construye una figura a tu gusto y calcula el volumen de la pirámide, del prisma y del conjunto

Ejercicio

Varía las alturas y calcula el volumen en 3 de los 14 al menos.

Ejercicio

Varía las alturas y calcula el volumen en 3 de los 14 al menos.

Restando

Varía la altura , las formas y calcula el volumen resultado.

Ejercicio

Varía las alturas y calcula el volumen en 3 de los 14 al menos.

Puzle de intercambio.

Imagen creada con Grok

ANEXO DE ÁREAS

Rectángulo

Observa que son 3 filas de 5 cuadraditos cada una.
Área = 3·5 = 15 Aquí puedes ampliar este anexo: Áreas de figuras planas

Resuelve el ejercicio propuesto

Triángulo

Observa que el triángulo ocupa la mitad del paralelogramo (dos triángulos iguales forman el cuadrilátero)

Trapecio

Dos trapecios iguales forman un rectángulo.
Resuelve el ejercicio propuesto.

Rombo

El área del rombo es la mitad del rectángulo que lo contiene.

Resuelve el ejercicio propuesto

Paralelogramo

Recortando un triángulo a la derecha y pegándolo a la izquierda construimos un rectángulo.
Resuelve el ejercicio propuesto.

Compuestas

Ejercicio.

En la página siguiente tienes 3 ejercicios resueltos (el 18, 19 y 20). Resuelve razonadamente al menos 5 de los comprendidos entre 1 y 17. En este trabajo no se han tratado ni figuras planas ni cuerpos con curvas. Si estás interesado te recomiendo: CÁLCULO DE ÁREAS DE REGIONES SOMBREADAS

Ejercicios resueltos.

• 

  A un rectángulo 6x4=24 se le recortan tres triángulos de áreas 1, 2 y 0,5.

  Área = 20,5

• 

  A un cuadrado 5x5=25 se le recortan dos trapecios de áreas 7 y 3.

  Área = 15

• 

  Podemos observar un cuadrado 6x6 al que se le han recortado cuatro triángulos 6x1 (de área 3).

  El área será A=24

Sopa de letra.

Imagen creada con Ideogram

CONSTRUCTORES

Constructor de prismas

Sigue estas indicaciones, visualiza el vídeo o simplemente trastea con la escena.

Constructor y multiplicador de prismas

Sigue estas indicaciones, visualiza el vídeo o simplemente trastea con la escena.

Ejercicio.

Costruye un prisma y multiplica este por 4, 9, 16 y 25. En cada caso busca el ángulo adecuado para hacer una captura de pantalla

Constructor de pirámides

Sigue estas indicaciones, visualiza el vídeo o simplemente trastea con la escena.

Constructor y multiplicador de pirámides

Sigue estas indicaciones, visualiza el vídeo o simplemente trastea con la escena.

Ejercicio.

Costruye una pirámide y multiplica esta por 4, 9, 16 y 25. En cada caso busca el ángulo adecuado para hacer una captura de pantalla

Constructor de prismas sobre un cubo.

Solo tienes que dibujar un polígono sobre el cuadriculado y pulsar [fin línea].

Constructor de pirámides sobre un cubo.

Solo tienes que dibujar un polígono sobre el cuadriculado y pulsar [fin línea].

Entretenimientos.

Niños jugando.

Escaparete.

Bibliografía online

Bibliografía. Libros.

Referencias a elementos usados en el libro.

Imágenes Grok.

Imágenes ideogram.

Imágenes del autor.