Mostrando artículos por etiqueta: inecuaciones
La unidad didáctica Inecuaciones del proyecto ed@d:
En Inecuaciones de 4º de la ESO (orientación enseñanzas académicas) del proyecto ed@d se definen las inecuaciones de primer y segundo grado con una y dos incógnitas y se indican diferentes formas de resolución tanto analítica como gráficamente, con muchos ejercicios y problemas para practicar.
En el vídeo de esta semana se presenta la unidad y se muestra el procedimiento a seguir para insertar esta unidad o partes de ella en un aula virtual, en este caso moodle.
Los materiales del proyecto ed@d abarcan todo el currículum de la enseñanza secundaria obligatoria para las asignaturas de Matemáticas, Ciencias de la Naturaleza y Física y Química. Estos materiales son idóneos para su uso en la formación a distancia y también en la formación presencial, ya sea en el aula o en casa.
Cada curso se estructura en torno a doce unidades temáticas. Todas las unidades de este proyecto siguen un mismo diseño. En la izquierda de la página inicial se encuentra el índice temático y en la parte superior un menú que da acceso a los diferentes apartados. También se puede descargar un cuaderno de trabajo y el documento pdf que recoge los contenidos desarrollados.
Para insertar la unidad en un aula virtual:
El código para embeber o abrir en ventana emergente de la unidad lo encontramos en la web de la RED.
|
En el menú superior de la página inicial seleccionamos Matemáticas/ed@d:
|
|
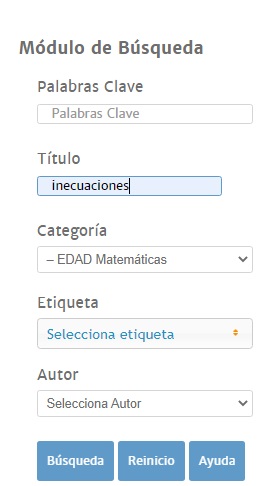
En el módulo de búsqueda escribimos el nombre de la unidad:
|
|
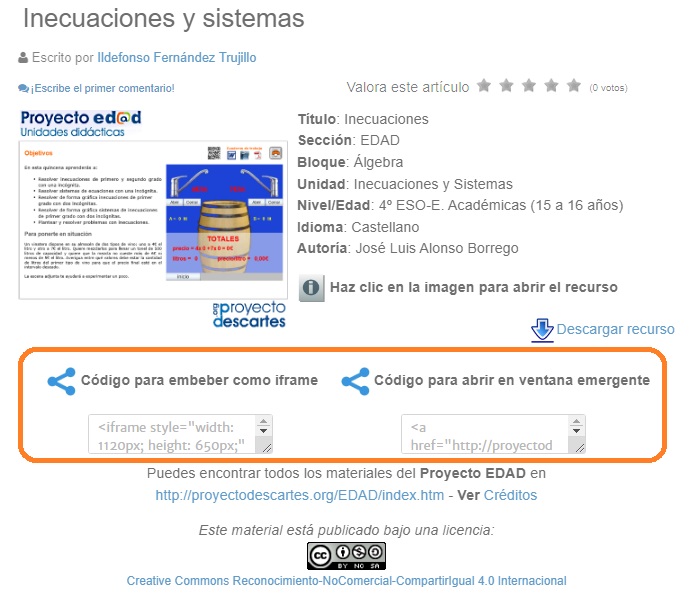
De esta forma accedemos a una página con información del objeto y los códigos para embeber y para abrir en ventana emergente. Elegimos uno de los códigos y lo insertamos en nuestra aula virtual: |
Si sólo nos interesa una página o una escena de ejercicios, usaremos los siguientes códigos:
Para embeber:
<iframe style="width: 810px; height: 585px;" src="/descartescms/ dirección web de la escena"></iframe>
Donde deberemos pegar la dirección de la escena
O para abrir en ventana emergente:
<a href="/descartescms/dirección web de la escena" target="_blank" onclick="window.open(this.href, this.target, 'width=1024,height=920,top=30,left=100,toolbar=0,menubar=0,scrollbars=1,resizable=1,location=0,status=0'); return false;"><img src="/descartescms/dirección de una imagen" alt="texto alternativo" style="display: block; margin-left: auto; margin-right: auto;"></a>
En este caso además de la dirección de la escena deberemos añadir la dirección de una imagen.
En el siguiente vídeo se muestra con detalle la unidad didáctica y el procedimiento a seguir para insertar estos objetos en moodle:
Título: Solución gráfica de desigualdades cuadráticas
Sección: Prometeo
Bloque: Álgebra
Unidad: Inecuaciones y sistemas
Nivel/Edad: Bachillerato y Universidad (17 años en adelante)
Idioma: Castellano
Redacción: Víctor Hugo García Jarillo
Programación: Víctor Hugo García Jarillo
Diseño gráfico: Said David Nájar Gil
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Prometeo en https://proyectodescartes.org/Prometeo/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Solución gráfica de desigualdades lineales
Sección: Prometeo
Bloque: Álgebra
Unidad: Inecuaciones y sistemas
Nivel/Edad: Bachillerato y Universidad (17 años en adelante)
Idioma: Castellano
Redacción: Joel Espinosa Longi
Programación: Joel Espinosa Longi
Diseño gráfico: Said David Nájar Gil
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Prometeo en https://proyectodescartes.org/Prometeo/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Resolución de una inecuación de dos variables
Sección: Miscelánea
Bloque: Álgebra
Unidad: Inecuaciones y sistemas
Nivel/Edad: 4º ESO (15 o más años)
Idioma: Castellano
Autoría: Rita Jiménez Igea
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales de la Miscelánea en
https://proyectodescartes.org/miscelanea/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri)







 CONTACTO
CONTACTO
