Mostrando artículos por etiqueta: problemas
ASIPISA es un proyecto de la Red Educativa Digital Descartes que comprende una serie de objetos digitales interactivos, elaborados a partir de una selección de unidades y preguntas liberadas del programa PISA, entre las utilizadas en el PISA 2000, prueba piloto de 2002 y PISA 2003.
Estos materiales incorporan aleatoriedad e interactividad a las cuestiones planteadas e incluyen la corrección del ejercicio al finalizar. Cada vez que se actualiza el objeto se modifican algunos elementos, lo cual permite que el estudiante pueda reutilizar una misma pregunta tantas veces como considere necesario.
Los materiales están clasificados en dos bloques: “Matemáticas” y “Lectura, Ciencias y Resolución de problemas”. En el siguiente vídeo se propone una selección de unidades del grupo de Resolución de problemas. Para su aplicación en el aula se muestra como insertar estas escenas en un curso Moodle.
Las unidades seleccionadas son:
Título: Cálculo de distancias inaccesibles
Sección: Prometeo
Bloque: Geometría
Unidad: Trigonometría
Nivel/Edad: 4º ESO (15 o más años)
Idioma: Castellano
Autoría: Fernando René Martínez Ortiz
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Prometeo en https://proyectodescartes.org/Prometeo/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Cálculo del ángulo de depresión
Sección: Prometeo
Bloque: Geometría
Unidad: Trigonometría
Nivel/Edad: 4º ESO (15 o más años)
Idioma: Castellano
Autoría: Fernando René Martínez Ortiz y Norma Patricia Apodaca Álvarez
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Prometeo en https://proyectodescartes.org/Prometeo/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Cálculo del ángulo de elevación
Sección: Prometeo
Bloque: Geometría
Unidad: Trigonometría
Nivel/Edad: 4º ESO (15 o más años)
Idioma: Castellano
Autoría: Fernando René Martínez Ortiz y Norma Patricia Apodaca Álvarez
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Prometeo en https://proyectodescartes.org/Prometeo/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Identificación de la ecuación cuadrática que modela un problema
Sección: Prometeo
Bloque: Álgebra
Unidad: Ecuaciones cuadráticas
Nivel/Edad: 3º ESO (14 o más años)
Idioma: Castellano
Autoría: Fernando René Martínez Ortiz
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Prometeo en https://proyectodescartes.org/Prometeo/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
El subproyecto Problemas del Proyecto Newton contiene una serie de unidades didácticas en las cuales se propone la resolución de diferentes problemas Física y Química para la ESO y el Bachillerato.
Todas las unidades han sido elaboradas siguiendo un mismo diseño, a partir del enunciado de un problema se aborda su resolución cuatro apartados:
Guía del alumno:
En este apartado se plantea el enunciado del problema y distintos puntos de vista sobre aspectos a tener en cuenta e indicaciones para su resolución.
Escenas interactivas:
Se proponen una o varias escenas para que el alumno pueda modificar los datos y comprobar el resultado utilizando las fórmulas correspondientes.
Evaluación:
Consta de uno o varios cuestionarios que hacen referencia al problema propuesto. El alumno puede comprobar si sus respuestas son correctas y repetir las actividades en caso de ser necesario.
Problema resuelto:
Se puede ver e imprimir el problema resuelto en pdf.
A modo de ejemplo, en el siguiente vídeo, se muestra una serie de unidades de dicho proyecto sobre el estudio de las diferentes centrales de producción de energía eléctrica para segundo de bachillerato: eólica, nuclear, térmica e hidroeléctrica.
También se indican los pasos a seguir para insertar estos elementos en un espacio virtual Moodle.
Aprendemos a resolver problemas con Descartes es una iniciativa del Departamento de Matemáticas del IES Bajo Guadalquivir de Lebrija, realizada con alumnos y alumnas de 4º ESO durante el curso escolar 2015/2016, basada en la experiencia para el "Desarrollo de la comunicación audiovisual a través de las Matemáticas con Descartes" y llevaba a cabo anteriormente con el alumnado de 1º de Bachillerato de Ciencias e Ingeniería, con objeto de fomentar en nuestros alumnos y alumnas el aprendizaje de las técnicas necesarias del lenguaje cinematográfico y audiovisual, a la vez que proporcionarles una formación básica que les permita, de forma autónoma, generar y producir sus propios contenidos audiovisuales.
Con el lema “Resolvemos problemas con Descartes“, abrimos un foro de suscripción forzosa en el aula virtual de Matemáticas-4º para coordinar la experiencia, dar las indicaciones, organizar los equipos, elegir los problemas, prestar asesoramiento y fomentar el trabajo en colaboración, aunque también se generaba debate en el día a día del aula física.
Decir que, durante todo el curso, los alumnos y alumnas asistieron a clase con sus portátiles de la Escuela TIC 2.0 que les entregaron cuando se encontraban en 5º de Primaria, usando junto a la PDI el libro digital interactivo del Proyecto ED@D y los cuadernos de trabajo Descartes que incorpora cada unidad interactiva, estando en contacto permanente con el profesor desde el aula virtual y desde la red social Twitter.
| 1ª FASE: PROPUESTA DE PROBLEMAS Y DIFUSIÓN EN TWITTER |
Cada equipo tuvo que seleccionar dos problemas de la unidad interactiva "Ecuaciones y sistemas", concretamente uno de primer grado y otro de segundo, que se encuentran en el menú ejercicios y que se denominan "Sistemas de ecuaciones lineales" y "Sistemas de segundo grado", respectivamente, y comunicarlo en el foro del aula virtual para conocimiento del profesor y del resto de equipos. Posteriormente, y una vez acordado con el profesor los dos problemas seleccionados para su resolución en lo que sería su "ópera prima", al menos en Matemáticas, tuvieron que diseñar una imagen alusiva al contenido de los problemas, incorporar sus enunciados y darle difusión por la red social Twitter con el hashtag del curso #MATES4ABAJO.
| 2ª FASE : DOCUMENTACIÓN Y GUIÓN DE LA OBRA |
Comienza la fase de investigación y documentación, así que damos las indicaciones desde el aula virtual, aportamos sugerencias, consejos y recomendamos espacios y recursos. Por ejemplo:
- Guía rápida para grabar en vídeo. ¡Muy bueno!
- Necesitáis un guión de lo que váis a grabar y a decir, pudiendo alternar planos virtuales de lo que se visualiza en el ordenador, tableta o smartphone con planos reales de la ejecución técnica de los ejercicios, que podéis realizar en una pizarra, en un cuaderno o folio, con un software que lo permita, grabando en interior o en exterior y, por supuesto, todo lo que se os ocurra. Aquí es donde entra en juego vuestra creatividad e imaginación.
- Recordad que publicaremos en internet el producto final, así que procurad la mejor calidad de imagen y audio posibles.
- El lenguaje matemático será primordial para las explicaciones y la comunicación audiovisual, por eso me enviaréis el borrador del guión, a través de la tarea del aula virtual, para que yo pueda revisarlo.
- No podéis usar ni imágenes ni música con derechos de autor. Para estos casos, os recomiendo:
- Banco de imágenes y sonidos del INTEF.
- Imágenes con licencia Creative Commons, del mismo banco anterior o de Pixabay.
- Jamendo, descarga de música libre y gratis.
- En cualquier caso, es recomendable dedicar una página de créditos para citar en el vídeo la autoría y el lugar de procedencia de las imágenes y audios usados.
- Debería aparecer, al menos, el logotipo del IES Bajo Guadalquivir, nuestro instituto.
- Cuando tengáis todo preparado y ensayado, os aconsejo hacer algunas pruebas de grabación cortas para comprobar si obtenéis el resultado deseado y las calidades demandadas
Si tenéis alguna idea y no sabéis cómo llevarla a efecto, podéis consultar en este foro o por el servicio de mensajería de la Moodle.
¡Es el momento de la CREATIVIDAD E IMAGINACIÓN!
| 3ª FASE : EVALUACIÓN |
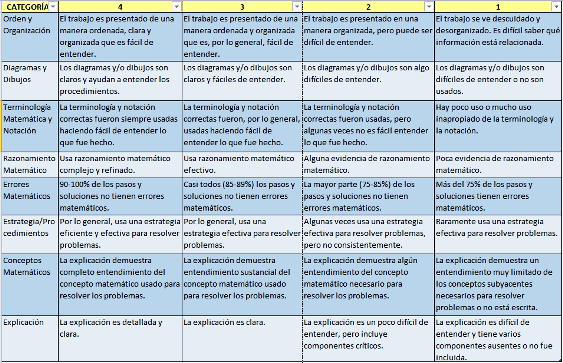
Para la evaluación relativa a los aspectos curriculares del producto final presentado por cada equipo, se ha utilizado la rúbrica que compartimos en este artículo, elaborada desde Rubistar, y que ya empleamos en la experiencia para el "Desarrollo de la comunicación audiovisual a través de las Matemáticas con Descartes". Con un clic sobre la imagen puede ampliarse para una correcta visualización.
Si visualizas y oyes el vídeo con detenimiento, sin duda, encontrarás leves errores de expresión escrita o verbal, tanto en el lenguaje ordinario como en el lenguaje matemático, lo que nos induce a dar una continuidad a la iniciativa y extrapolarla a otros cursos para ir consiguiendo nuestro objetivo paulatinamente. Además, la localización y análisis de errores es una de las mejores estrategias de aprendizaje. No obstante, quiero desde aquí felicitar a todos mis alumnos y alumnas de 4º A por sorprenderme con su creatividad e imaginación, por ser competentes para generar contenido multimedia con sus dispositivos móviles, sin que su profesor sepa ayudarles en este ámbito, por afrontar todos los retos que se han encontrado por el camino hasta conseguir el producto final y por permitirme descubrir y fomentar algunas de sus capacidades ocultas.
Muchas gracias también a sus familias por apoyar la iniciativa autorizando las grabaciones y su difusión por las redes sociales, lo que obviamente repercute en una mejora de la formación de sus hijos e hijas como ciudadanos y ciudadanas del s. XXI y en su preparación para la siguiente etapa educativa.
Volvemos a visitar la zona de problemas del Proyecto Newton para revisar Energía electrica: central hidroeléctrica de Mª Josefa Grima Rojas y Javier Soriano

Es un problema que se centra en la producción de energía a partir del agua que acumulamos en un embalse.
Se trabajan los conceptos de tipos de energía, transformaciones, rendimiento, ventajas y problemas de esta generación y también ejercicios numéricos.
Cada apartado del problema propuesto viene completado con una pregunta que aporta posibles soluciones, todas comentadas explicando el error cometido o ampliando el acierto.
Las preguntas son muy variadas, van desde razonamientos o explicaciones a deducción de fórmulas o cálculos.
Se trata de un problema muy completo que mejora todavía más con las animaciones y la escena interactiva.
Como en todos los problemas disponemos de una autoevaluación y del problema resuelto en PDF.
Os dejamos el vídeo que comenta el problema:
Seguro que os resulta muy útil
Dispones de muchos más recursos en la web del Protecto Descartes
Dentro del proyecto Problemas de Física y Química hoy vamos a revisar Poleas

Se trata de un problema que podemos trabajar tanto en 4º de ESO como en 1º de bachillerato,
si despreciamos la masa de la polea, y en 2º de bachillerato ,si la tenemos en cuenta.
Como en todos los materiales de este subproyecto encontramos una introducción, una guía del alumno, una animación interactiva, una evaluación con autocorrección y el problema resuleto en formato PDF.
El problema elegido consta de dos masas unidas por una cuerda ideal que pasa por una polea y una de ellas descansa en un plano inclinado.
Se indican los pasos a realizar en la resolución para calcular la tensión y la aceleración. En primer lugar se desprecia el efecto de la polea, luego se incluye y finalmente se tenie en cuenta también el rozamiento.
El alumno dispone de esquemas con las fuerzas y su descomposición que facilitan la comprensión de la resolución.
La escena interactiva permite la variación de los valores de las dos masas, el ángulo del plano inclinado y el coeficiente de rozamiento.
Para el segundo caso hay otra escena en la que aparece un nuevo parámetro modificable, la masa de la polea.
La autoevaluación incluye preguntas de opción múltiple, alguna apoyada con su propia escena interactiva.
A continuación te dejamos un vídeo que comenta todas las partes de las páginas que componen este objeto interactivo.
El problema lo puedes descargar aquí
Recuerda que disponemos de muchos más problemas en las páginas del proyecto.
Utlízalos.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri)






 CONTACTO
CONTACTO
