Física - Volumen I
INTERACTIVO
Juan Guillermo Rivera Berrío
Institución Universitaria Pascual Bravo
Red Educativa Digital Descartes
Fondo Editorial RED Descartes

Córdoba (España)
2022
Título de la obra:
Física - Volumen I
Interactivo
Autor:
Juan Guillermo Rivera Berrío
Obra derivada del libro University Physics - Volume I
Samuel J. Ling (Truman State University)
Jeff Sanny (Loyola Marymount University)
Bill Moebs
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Amaranth y UbuntuMono
Fórmulas matemáticas: $\KaTeX$
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
ISBN Obra completa: 978-84-18834-39-4
ISBN Volumen I: 978-84-18834-40-0

Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.
Tabla de contenido
Enrico Fermi (Roma, 29 de septiembre de 1901-Chicago, 28 de noviembre de 1954) fue un físico Italiano conocido por el desarrollo del primer reactor nuclear y sus contribuciones al desarrollo de la teoría cuántica (https://commons.wikimedia.org/).
Prefacio
Este libro digital interactivo se ha diseñado con fundamento en la filosofía del Proyecto Descartes: "Trabajando altruistamente por la comunidad educativa de la aldea global", que sólo busca desarrollar contenidos educativos para el provecho de la comunidad académica, esperando únicamente como retribución el uso y difusión de estos contenidos. El contenido del libro, al igual que los objetos interactivos se han diseñado de tal forma que se puedan leer en ordenadores y dispositivos móviles sin necesidad de instalar ningún programa o plugin. El libro se puede descargar para su uso en local sin dependencia con la red, a excepción de los ocho vídeos incluidos en el texto.
El contenido del libro se basa en un recurso de OpenStax, organización sin fines de lucro de la Universidad de Rice, cuya misión, similar a la nuestra, es mejorar el acceso de los estudiantes a la educación. El libro ha sido desarrollado para cumplir con el alcance y la secuencia de la mayoría de los cursos de física universitarios y proporciona una base para una carrera en matemáticas, ciencias o ingeniería.
Este primer volumen del libro de texto de Física Universitaria se adhiere al alcance y la secuencia de un primer curso de física. Se ha trabajado para hacer que la física sea interesante y accesible para los estudiantes, manteniendo el rigor matemático inherente a la materia. Con este objetivo en mente, el contenido de este libro de texto ha sido desarrollado y organizado para proporcionar una progresión lógica de conceptos fundamentales a más avanzados, basándose en lo que los alumnos ya han aprendido y enfatizando las conexiones entre los temas y entre la teoría y las aplicaciones. El objetivo de cada sección es permitir que los estudiantes no solo reconozcan conceptos, sino que trabajen con ellos de manera que sean útiles en cursos posteriores y carreras futuras. La organización y las características pedagógicas fueron desarrolladas y revisadas con comentarios de educadores de ciencias dedicados al proyecto.
A lo largo del libro encontrarás derivaciones de conceptos que presentan ideas y técnicas clásicas, así como también aplicaciones y métodos modernos. La mayoría de los capítulos comienzan con observaciones o experimentos que colocan el material en un contexto de experiencia física. Las presentaciones y explicaciones se basan en años de experiencia en el aula por parte de profesores de física de larga data, que luchan por un equilibrio de claridad y rigor que ha demostrado ser exitoso con sus alumnos. Las figuras históricas clave y los experimentos se discuten en el texto principal, manteniendo un enfoque en el desarrollo de la intuición física. Las ideas clave, las definiciones y las ecuaciones se destacan en el texto.
Los ejemplos y las imágenes de apertura de capítulos a menudo incluyen aplicaciones contemporáneas de la vida cotidiana o de la ciencia y la ingeniería modernas con las que los estudiantes se pueden relacionar, desde teléfonos inteligentes hasta Internet y dispositivos GPS.
El texto original, desarrollado por Ling S., Sanny J. y Moebs B., ha sido publicado en versiones html y pdf. Esta obra derivada, en español y como libro interactivo, creada por Rivera J.G., presenta las siguientes aportaciones: traducción al español, inclusión de herramientas, incorporación de 56 objetos interactivos de aprendizaje, 36 de ellos diseñados con el editor DescartesJS, y ocho vídeos. Para evitar, al máximo, la dependencia con la conectividad en la red, las expresiones matemáticas se han construido recurriendo a la librería $\KaTeX$. Incluye, además, la posibilidad de imprimir el libro o guardarlo como un archivo en formato PDF.
Se ha conservado la propuesta pedagógica en los ejemplos presentados en cada uno de los capítulos, los cuales incluyen: formulación del problema, estrategia de solución, solución, explicación o sentido de los resultados obtenidos y, en la mayoría de los ejemplos, un problema propuesto, denominado "Comprueba tu aprendizaje". Al final de cada capítulo se han incluido tanto los problemas propuestos como las respuestas.
Unidades y medición
Marie Curie o Madame Curie (Varsovia, 7 de noviembre de 1867-Passy, 4 de julio de 1934), fue una física y química polaca nacionalizada francesa. Pionera en el campo de la radiactividad, fue la primera persona en recibir dos premios Nobel en distintas especialidades: Física y Química (https://es.wikipedia.org/)
Unidades y medición
Introducción

Como se indica en la leyenda de la figura, la imagen de apertura de este capítulo es de la galaxia Whirlpool. Las galaxias son tan grandes como pequeños son los átomos, pero las mismas leyes de la física las describen a ambos, junto con el resto de la naturaleza.
Las leyes de la física son sorprendentemente pocas, lo que implica una simplicidad subyacente a la aparente complejidad de la naturaleza. En este libro, aprenderás sobre las leyes de la física.
Puede parecer que las galaxias y átomos están muy alejados de tu vida diaria, pero a medida que comienzas a explorar este vasto tema, pronto te darás cuenta de que la física juega un papel mucho más importante de lo que creías, sin importar los objetivos de tu vida, o elección de carrera.
El alcance de la Física
La física está dedicada a la comprensión de todos los fenómenos naturales. En la física, tratamos de comprender los fenómenos físicos en todas las escalas, desde el mundo de las partículas subatómicas hasta el universo entero. A pesar de la amplitud del tema, los diversos subcampos de la física comparten un núcleo común. La misma formación básica en física te preparará para trabajar en cualquier área de la física y las áreas relacionadas de ciencia e ingeniería. En esta sección, investigamos el alcance de la física; las escalas de longitud, masa y tiempo durante las cuales las leyes de la física han demostrado ser aplicables; y el proceso por el cual opera la ciencia en general, y la física en particular.
Dale otro vistazo a la imagen de apertura de capítulo. La galaxia Whirlpool contiene miles de millones de estrellas individuales y enormes nubes de gas y polvo. Su galaxia compañera también es visible a la derecha. Este par de galaxias se encuentran en un asombroso billón de billones de millas ($1.4 \times 10^{21}\;mi$) de nuestra propia galaxia (que se llama la Vía Láctea). Las estrellas y los planetas que componen la Galaxia Whirlpool pueden parecer lo más alejado de la vida cotidiana de la mayoría de la gente, pero la Whirlpool es un gran punto de partida para pensar en las fuerzas que mantienen unido al universo. Se cree que las fuerzas que causan que la Galaxia Whirlpool actúe como lo hace, son las mismas fuerzas con las que lidiamos aquí en la Tierra, ya sea que planeemos enviar un cohete al espacio o simplemente levantar las paredes para un nuevo hogar.
Se cree que la gravedad que causa que las estrellas de la Galaxia Whirlpool giren y giren es la misma que hace que el agua fluya sobre las represas hidroeléctricas aquí en la Tierra. Cuando miras hacia las estrellas, date cuenta de que las fuerzas que existen son las mismas que aquí en la Tierra. A través de un estudio de física, puedes obtener una mayor comprensión de la interconexión de todo lo que podemos ver y conocer en este universo. Piensa, ahora, sobre todos los dispositivos tecnológicos que usas regularmente. Podrían venir a la mente computadoras, teléfonos inteligentes, sistemas de posicionamiento global (GPS), reproductores de MP3 y radio satelital. Luego, piensa en las tecnologías modernas más interesantes de las que has oído hablar en las noticias, como los trenes que levitan por encima de las vías, las "capas de invisibilidad" que doblan la luz a su alrededor y los robots microscópicos que combaten las células cancerosas en nuestros cuerpos. Todos estos avances revolucionarios, comunes o increíbles, se basan en los principios de la física. Además de jugar un papel importante en la tecnología, profesionales como ingenieros, pilotos, médicos, fisioterapeutas, electricistas y programadores de computadoras aplican conceptos de física en su trabajo diario. Por ejemplo, un piloto debe comprender cómo las fuerzas del viento afectan una trayectoria de vuelo; un fisioterapeuta debe comprender cómo los músculos en el cuerpo experimentan fuerzas a medida que se mueven y se doblan. Como aprenderás en este texto, los principios de la física están impulsando nuevas y emocionantes tecnologías, y estos principios se aplican en una amplia gama de carreras.
El orden subyacente de la naturaleza hace que la ciencia en general, y la física en particular, sean interesantes y agradables de estudiar. Por ejemplo, ¿qué tienen en común una bolsa de papas fritas y una batería de automóvil? Ambos contienen energía que se puede convertir a otras formas.
La ley de la conservación de la energía (que dice que la energía puede cambiar de forma pero nunca se pierde) vincula temas tales como calorías de alimentos, baterías, calor, luz y muelles de observación. Comprender esta ley hace que sea más fácil aprender sobre las diversas formas que toma la energía y cómo se relacionan entre sí. Aparentemente, temas no relacionados están conectados a través de leyes físicas ampliamente aplicables, lo que permite una comprensión más allá de la mera memorización de listas de hechos.
La ciencia consiste en teorías y leyes que son las verdades generales de la naturaleza, así como el cuerpo de conocimiento que abarcan. Los científicos intentan continuamente expandir este cuerpo de conocimiento y perfeccionar la expresión de las leyes que lo describen. La física, que proviene del griego phúsis, que significa "naturaleza", se refiere a describir las interacciones de la energía, la materia, el espacio y el tiempo para descubrir los mecanismos fundamentales que subyacen a cada fenómeno. Esta preocupación por describir los fenómenos básicos en la naturaleza define esencialmente el alcance de la física.
La física tiene como objetivo comprender el mundo que nos rodea en el nivel más básico. Hace hincapié en el uso de un pequeño número de leyes cuantitativas para hacer esto, lo que puede ser útil para otros campos que impulsan los límites de rendimiento de las tecnologías existentes. Considera un teléfono inteligente (Figura 1.2). La física describe cómo la electricidad interactúa con los diversos circuitos dentro del dispositivo. Este conocimiento ayuda a los ingenieros a seleccionar los materiales adecuados y el diseño del circuito al construir un teléfono inteligente. El conocimiento de la física subyacente a estos dispositivos es necesario para reducir su tamaño o aumentar su velocidad de procesamiento. O piense en un GPS. La física describe la relación entre la velocidad de un objeto, la distancia sobre la que viaja y el tiempo que lleva recorrer esa distancia.
Cuando usas un GPS en un vehículo, se basa en ecuaciones de física para determinar el tiempo de viaje de un lugar a otro.
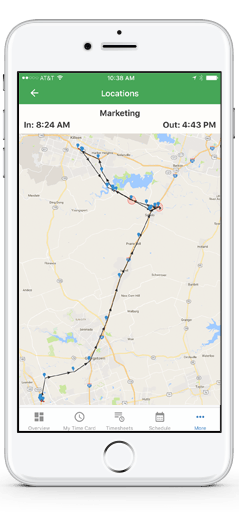
El conocimiento de la física es útil en situaciones cotidianas, así como en profesiones no científicas. Puede ayudarte a comprender cómo funcionan los hornos de microondas, por qué no deben colocarse metales y por qué podrían afectar los marcapasos. La física te permite comprender los peligros de la radiación y evaluar estos peligros de forma racional y más fácil. La física también explica la razón por la cual un radiador de automóvil negro ayuda a eliminar el calor en el motor de un automóvil, y explica por qué un techo blanco ayuda a mantener fresco el interior de una casa.
Del mismo modo, la operación del sistema de encendido de un automóvil y la transmisión de señales eléctricas a través del sistema nervioso de nuestro cuerpo son mucho más fáciles de entender cuando se piensa en ellos en términos de física básica.
La física es un elemento clave de muchas disciplinas importantes y contribuye directamente a las demás. La química, por ejemplo, que se ocupa de las interacciones de átomos y moléculas, tiene estrechos vínculos con la física atómica y molecular. La mayoría de las ramas de la ingeniería se preocupan por el diseño de nuevas tecnologías, procesos o estructuras dentro de las limitaciones establecidas por las leyes de la física. En arquitectura, la física está en el corazón de la estabilidad estructural y está involucrada en la acústica, el calentamiento, la iluminación y el enfriamiento de los edificios. Algunas partes de la geología dependen en gran medida de la física, como la datación radioactiva de rocas, el análisis de terremotos y la transferencia de calor dentro de la Tierra. Algunas disciplinas, como la biofísica y la geofísica, son híbridos de la física y otras disciplinas.
La física tiene muchas aplicaciones en las ciencias biológicas. En el nivel microscópico, ayuda a describir las propiedades de las células y sus entornos. En el nivel macroscópico, explica el calor, el trabajo y la potencia asociados con el cuerpo humano y sus diversos sistemas orgánicos. La física participa en diagnósticos médicos, como radiografías, imágenes de resonancia magnética y mediciones de flujo sanguíneo ultrasónico. La terapia médica a veces involucra la física directamente; por ejemplo, la radioterapia contra el cáncer utiliza radiación ionizante. La física también explica los fenómenos sensoriales, como la forma en que los instrumentos musicales hacen el sonido, cómo el ojo detecta el color y cómo los láseres transmiten información.
No es necesario estudiar todas las aplicaciones de la física formalmente.
Lo más útil es conocer las leyes básicas y desarrollar habilidades en los métodos analíticos para aplicarlas. El estudio de la física también puede mejorar tus habilidades para resolver problemas.
La escala de la física
Hasta ahora, debe quedar claro que para lograr sus objetivos en cualquiera de los diversos campos dentro de las ciencias naturales y la ingeniería, es necesaria una sólida base en las leyes de la física. La razón de esto es simplemente que las leyes de la física gobiernan todo en el universo observable en todas las escalas mensurables de longitud, masa y tiempo. Ahora, eso es bastante fácil de decir, pero para entender lo que realmente significa, necesitamos ser un poco cuantitativos. Entonces, antes de examinar las diversas escalas, veamos el concepto de "orden de magnitud", que usamos para llegar a un acuerdo con los vastos intervalos de longitud, masa y tiempo que consideramos en este libro (Figura 1.3).

Orden de magnitud
El orden de magnitud se refiere a la escala (o tamaño) de un valor. Cada potencia de 10 representa un orden de magnitud diferente. Por ejemplo, $10^1, 10^2, 10^3$, y así sucesivamente, son todos órdenes de magnitud diferentes, como lo son $10^0 = 1, 10^{-1}, 10^{-2}$, y $10^{-3}$. Para encontrar el orden de magnitud de un número, toma el logaritmo de base 10 del número y redondéalo al entero más cercano, entonces el orden de magnitud del número es simplemente la potencia resultante de $10$. Por ejemplo, el orden de magnitud de $800$ es $10^3$ porque $log_{10}800 \approx 2.903$, que se redondea a $3$. De forma similar, el orden de magnitud de $450$ es $10^3$ porque $log_{10}450 \approx 2.653$, que se redondea a $3$ también. Por lo tanto, decimos que los números $800$ y $450$ son del mismo orden de magnitud: $10^3$. Sin embargo, el orden de magnitud de $250$ es $10^2$ porque $log_{10}250 \approx 2.397$, que se redondea a $2$.
Una forma equivalente pero más rápida de encontrar el orden de magnitud de un número es primero escribirlo en notación científica y luego verificar si el primer factor es mayor o menor que $\sqrt{10} = 10^{0.5} \approx 3.10$. La idea es que $\sqrt{10} = 10^{0.5}$ está a medio camino entre $1 = 10^0$ y $10 = 10^1$ en una escala logarítmica base $10$. Por lo tanto, si el primer factor es menor que $\sqrt{10}$, lo redondeamos a $1$ y el orden de magnitud es simplemente cualquier potencia de $10$ que se requiera para escribir el número en notación científica. Por otro lado, si el primer factor es mayor que $\sqrt{10}$, lo redondeamos a $10$ y el orden de magnitud es una potencia de $10$ más que la potencia necesaria para escribir el número en notación científica. Por ejemplo, el número $800$ se puede escribir en notación científica como $8 \times 10^2$. Como $8$ es mayor que $\sqrt{10} \approx 3,10 \approx 3$, decimos que el orden de magnitud de $800$ es $10^{2 + 1} = 10^3$. El número $450$ se puede escribir como $4.5 × 10^2$, por lo que su orden de magnitud es también $10^3$ porque $4.5$ es mayor que $3$.
Sin embargo, $250$ escrito en notación científica es $2.5 \times 10^2$ y $2.5$ es menor que $3$, entonces su orden de magnitud es $10^2$.
El orden de magnitud de un número está diseñado para ser una estimación aproximada de la escala (o tamaño) de su valor. Es simplemente una manera de redondear los números consistentemente al poder más cercano de 10. Esto hace que sea más fácil hacer cálculos mentales difíciles con números muy grandes y muy pequeños. Por ejemplo, el diámetro de un átomo de hidrógeno es del orden de $10^{-10}\; m$, mientras que el diámetro del Sol es del orden de $10^9\; m$, por lo que tomaría aproximadamente $10^9 / 10^{-10} = 10^{19}$ átomos de hidrógeno para estirar a través del diámetro del sol. Esto es mucho más fácil de hacer en tu cabeza que usar los valores más precisos de $1.06 \times 10^{-10}\;m$ para un diámetro de átomo de hidrógeno y $1.39 \times 10^9\;m$ para el diámetro del Sol, para encontrar que lo haría tome $1.31 \times 10^{19}$ átomos de hidrógeno para estirar a través del diámetro del Sol. Además de ser más fácil, la estimación aproximada también es casi tan informativa como el cálculo preciso.
Rangos conocidos de longitud, masa y tiempo
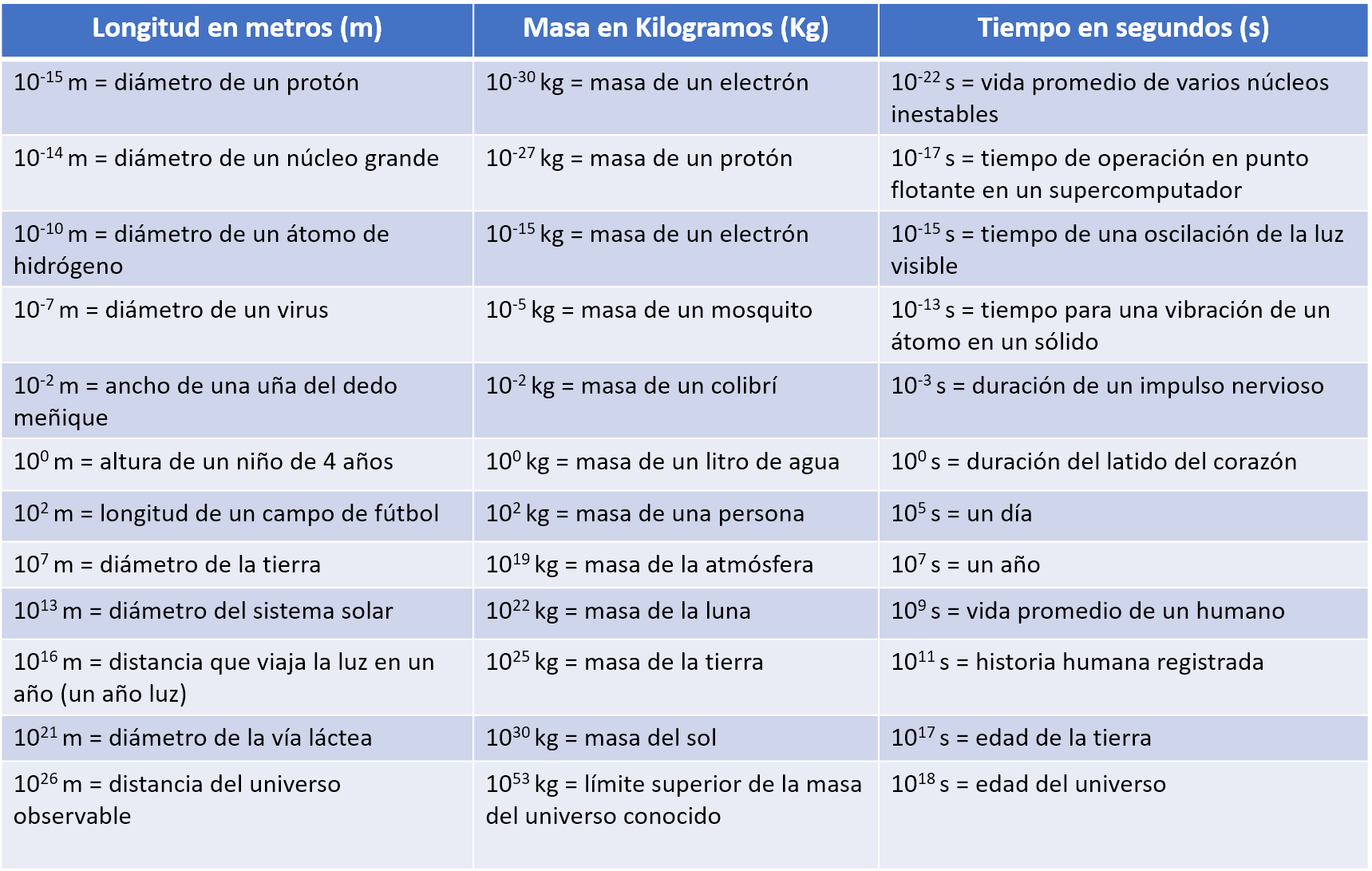
La vastedad del universo y la amplitud a la que se aplica la física se ilustran mediante la amplia gama de ejemplos de longitudes, masas y tiempos conocidos (dados como órdenes de magnitud) en la Figura 1.4. Examinar esta tabla te dará una idea del rango de posibles temas en física y valores numéricos. Una buena forma de apreciar la vastedad de los rangos de valores en la Figura 1.4 es tratar de responder algunas preguntas comparativas simples, como las siguientes:
- ¿Cuántos átomos de hidrógeno se necesitan para estirar a través del diámetro del Sol? (Respuesta: $10^9\;m / 10^{-10}\; m = 10^{19}$ átomos de hidrógeno)
- ¿Cuántos protones hay en una bacteria? (Respuesta: $10^{-15}\; kg / 10^{-27}\; kg = 10^{12}$ protones)
- ¿Cuántas operaciones de punto flotante puede hacer una supercomputadora en 1 día? (Respuesta: $10^5\; s /10 ^{17}\; s = 10^{22}$ operaciones de coma flotante)
Al estudiar la Figura 1.4, tómate un tiempo para formular preguntas similares que te interesen y luego intenta responderlas.
En el siguiente vídeo observa la amplia gama de escalas de longitud en nuestro universo. En la escala podrás ver cientos de organismos y objetos.
Video
La construcción de modelos
¿Cómo llegamos a conocer las leyes que gobiernan los fenómenos naturales? A lo que nos referimos como las leyes de la naturaleza son descripciones concisas del universo que nos rodea. Son declaraciones humanas de las leyes o reglas subyacentes que siguen todos los procesos naturales. Tales leyes son intrínsecas al universo; los humanos no las crearon y no pueden cambiarlas. Solo podemos descubrirlas y entenderlas. Su descubrimiento es un esfuerzo muy humano, con todos los elementos de misterio, imaginación, lucha, triunfo y decepción inherentes a cualquier esfuerzo creativo (Figura 1.5).
La piedra angular del descubrimiento de las leyes naturales es la observación; los científicos deben describir el universo tal como es, no como imaginamos que es.

Un modelo es una representación de algo que a menudo es demasiado difícil (o imposible) de mostrar directamente. Aunque un modelo está justificado por pruebas experimentales, solo es preciso al describir ciertos aspectos de un sistema físico.
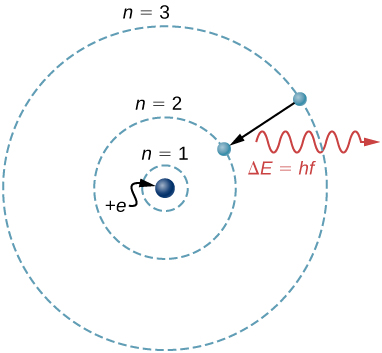
Un ejemplo es el modelo de Bohr de átomos de un solo electrón, en el que el electrón se representa como una órbita alrededor del núcleo, análoga a la forma en que los planetas orbitan el Sol (Figura 1.6). No podemos observar las órbitas de los electrones directamente, pero la imagen mental ayuda a explicar algunas de las observaciones que podemos hacer, como la emisión de luz de los gases calientes (espectros atómicos). Sin embargo, otras observaciones muestran que la imagen en el modelo de Bohr no es en realidad a qué se parecen los átomos. El modelo es "incorrecto", pero sigue siendo útil para algunos propósitos. Los físicos usan modelos para una variedad de propósitos. Por ejemplo, los modelos pueden ayudar a los físicos a analizar un escenario y realizar un cálculo o pueden usarse modelos para representar una situación en forma de simulación por computadora. En última instancia, sin embargo, los resultados de estos cálculos y simulaciones deben verificarse por otros medios, a saber, la observación y la experimentación.
La palabra teoría significa algo diferente para los científicos de lo que a menudo se entiende cuando la palabra se usa en la conversación cotidiana. En particular, para un científico, una teoría no es lo mismo que una "adivinanza" o una "idea" o incluso una "hipótesis". La frase "es solo una teoría" parece absurda y tonta para los científicos porque la ciencia se basa en la noción de teorías. Para un científico, una teoría es una explicación comprobable de patrones en la naturaleza respaldados por evidencia científica y verificados varias veces por varios grupos de investigadores. Algunas teorías incluyen modelos para ayudar a visualizar los fenómenos mientras que otros no. La teoría de la gravedad de Newton, por ejemplo, no requiere un modelo o imagen mental, porque podemos observar los objetos directamente con nuestros propios sentidos. La teoría cinética de los gases, por otro lado, es un modelo en el que se considera que un gas está compuesto de átomos y moléculas. Los átomos y las moléculas son demasiado pequeños para ser observados directamente con nuestros sentidos, por lo tanto, los imaginamos mentalmente para comprender lo que los instrumentos nos dicen sobre el comportamiento de los gases. Aunque los modelos están destinados solo a describir ciertos aspectos de un sistema físico con precisión, una teoría debe describir todos los aspectos de cualquier sistema que caiga dentro de su dominio de aplicabilidad. En particular, cualquier implicación comprobable experimentalmente de una teoría debe ser verificada. Si un experimento alguna vez demuestra que una implicación de una teoría es falsa, entonces la teoría es descartada o modificada adecuadamente (por ejemplo, limitando su dominio de aplicabilidad).
Una ley usa lenguaje conciso para describir un patrón generalizado en la naturaleza respaldado por evidencia científica y experimentos repetidos. A menudo, una ley se puede expresar en forma de una ecuación matemática única. Las leyes y las teorías son similares en que ambas son declaraciones científicas que resultan de una hipótesis probada y están respaldadas por evidencia científica.
Sin embargo, la ley de designación generalmente se reserva para una declaración concisa y muy general que describe fenómenos en la naturaleza, como la ley de conservación de la energía, o la segunda ley de movimiento de Newton.
Una teoría, por contraste, es una declaración menos concisa del comportamiento observado. Por ejemplo, la teoría de la evolución y la teoría de la relatividad no pueden expresarse lo suficientemente concisas como para ser consideradas leyes. La mayor diferencia entre una ley y una teoría es que una teoría es mucho más compleja y dinámica. Una ley describe una sola acción, mientras que una teoría explica todo un grupo de fenómenos relacionados. En general, las declaraciones menos aplicables se denominan principios (como el principio de Pascal, que solo se aplica a los fluidos), pero a menudo la distinción entre leyes y principios no se hace con cuidado.
Los modelos, teorías y leyes que diseñamos a veces implican la existencia de objetos o fenómenos que aún no se observan. Estas predicciones son notables triunfos y tributos al poder de la ciencia. Es el orden subyacente en el universo que permite a los científicos hacer predicciones tan espectaculares. Sin embargo, si la experimentación no verifica nuestras predicciones, entonces la teoría o ley es incorrecta, sin importar cuán elegante o conveniente sea. Las leyes nunca pueden conocerse con absoluta certeza porque es imposible realizar todos los experimentos imaginables para confirmar una ley para cada escenario posible. Los físicos operan bajo el supuesto de que todas las leyes y teorías científicas son válidas hasta que se observe un contraejemplo. Si un experimento de buena calidad y verificable contradice una ley o teoría bien establecida, entonces la ley o teoría debe ser modificada o derrocada por completo.
El estudio de la ciencia en general, y la física en particular, es una aventura muy parecida a la exploración de un océano inexplorado.
Los descubrimientos están hechos; modelos, teorías y leyes están formuladas; y la belleza del universo físico se hace más sublime por los conocimientos adquiridos.
En la siguiente escena, podrás observar algunos modelos sobre el átomo.
¡Haz clic en el botón de la esquina superior derecha, para ampliar la escena!
Unidades y estándares
Como vimos anteriormente, la gama de objetos y fenómenos estudiados en física es inmensa. Desde la increíblemente corta vida de un núcleo hasta la edad de la Tierra, desde los diminutos tamaños de partículas subnucleares hasta la vasta distancia hasta los bordes del universo conocido, desde la fuerza ejercida por una pulga saltadora hasta la fuerza entre la Tierra y el Sol, hay suficientes factores de 10 para desafiar la imaginación de incluso el científico más experimentado. Dar valores numéricos para cantidades físicas y ecuaciones para principios físicos nos permite comprender la naturaleza mucho más profundamente que las descripciones cualitativas solos. Para comprender estos vastos rangos, también debemos haber aceptado unidades en las que expresarlos. Encontraremos que incluso en la discusión potencialmente mundana de metros, kilogramos y segundos, aparece una profunda simplicidad de la naturaleza: todas las cantidades físicas se pueden expresar como combinaciones de solo siete cantidades físicas básicas.
Definimos una cantidad física ya sea especificando cómo se mide o indicando cómo se calcula a partir de otras mediciones. Por ejemplo, podríamos definir la distancia y el tiempo especificando los métodos para medirlos, como usar un metro y un cronómetro. Entonces, podríamos definir la velocidad promedio indicando que se calcula como la distancia total recorrida dividida por el tiempo de viaje.
Las mediciones de las cantidades físicas se expresan en términos de unidades, que son valores estandarizados. Por ejemplo, la longitud de una carrera, que es una cantidad física, se puede expresar en unidades de metros (para velocistas) o kilómetros (para corredores de distancia). Sin unidades estandarizadas, sería extremadamente difícil para los científicos expresar y comparar valores medidos de una manera significativa (Figura 1.7).
enloquecedoramente inútiles.
En el mundo se utilizan dos sistemas principales de unidades: unidades SI (para el sistema francés Système International d'Unités), también conocido como el sistema métrico, y unidades inglesas (también conocidas como sistema consuetudinario o imperial). Las unidades inglesas se usaron históricamente en naciones una vez gobernadas por el Imperio británico y todavía se usan ampliamente en los Estados Unidos. Las unidades en inglés también pueden denominarse sistema pie-libra-segundo (fps), a diferencia del sistema centímetro-gramo-segundo (cgs). También puedes encontrar el término unidades SAE, que lleva el nombre de la Sociedad de Ingenieros Automotrices. Productos como sujetadores y herramientas automotrices (por ejemplo, llaves inglesas) que se miden en pulgadas en lugar de en unidades métricas se conocen como sujetadores SAE o llaves SAE.
Prácticamente todos los demás países del mundo (excepto los Estados Unidos) ahora usan unidades SI como estándar. El sistema métrico es también el sistema estándar acordado por científicos y matemáticos.
Unidades SI: Base y Unidades Derivadas
En cualquier sistema de unidades, las unidades para algunas cantidades físicas se deben definir a través de un proceso de medición. Éstas se llaman las cantidades base para ese sistema y sus unidades son la base del sistema. Todas las demás cantidades físicas pueden expresarse como combinaciones algebraicas de las cantidades base. Cada una de estas cantidades físicas se conoce como una cantidad derivada y cada unidad se denomina unidad derivada. La elección de cantidades base es algo arbitraria, siempre que sean independientes entre sí y todas las demás cantidades puedan derivarse de ellas. Por lo general, el objetivo es elegir cantidades físicas que se puedan medir con una precisión alta como las cantidades base. La razón de esto es simple. Como las unidades derivadas se pueden expresar como combinaciones algebraicas de las unidades base, solo pueden ser tan precisas como las unidades base de las que se derivan.
Sobre la base de tales consideraciones, la Organización Internacional de Normalización recomienda utilizar siete cantidades básicas, que forman el Sistema Internacional de Cantidades (ISQ). Estas son las cantidades base utilizadas para definir las unidades base SI. La Tabla 1.1 enumera estas siete cantidades de base ISQ y las unidades base SI correspondientes.
Probablemente ya estés familiarizado con algunas cantidades derivadas que se pueden formar a partir de las cantidades base en la Tabla 1.1. Por ejemplo, el concepto geométrico de área siempre se calcula como el producto de dos longitudes.
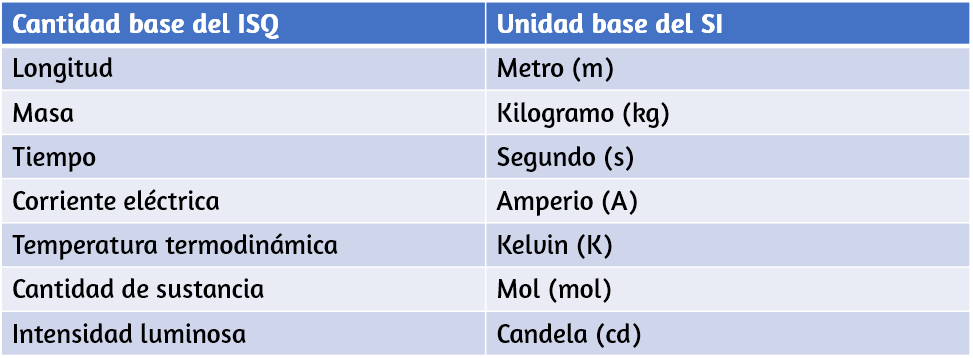
Probablemente ya estés familiarizado con algunas cantidades derivadas que se pueden formar a partir de las cantidades base en la Tabla 1.1. Por ejemplo, el concepto geométrico de área siempre se calcula como el producto de dos longitudes. Por lo tanto, el área es una cantidad derivada que se puede expresar en términos de unidades base SI, utilizando metros cuadrados ($m\times m = m^2$). Del mismo modo, el volumen es una cantidad derivada que se puede expresar en metros cúbicos ($m^3$). La velocidad es la longitud por unidad de tiempo; entonces, en términos de unidades base SI, podríamos medirlo en metros por segundo ($m/s$). La densidad de masa del volumen (o solo la densidad) es la masa por volumen, que se expresa en términos de unidades de base SI, como kilogramos por metro cúbico ($kg / m^3$). Los ángulos también pueden considerarse cantidades derivadas porque se pueden definir como la relación de la longitud del arco subtendida por dos radios de un círculo al radio del círculo. Así es como se define el radián. Dependiendo de tus antecedentes e intereses, es posible que puedas obtener otras cantidades derivadas, como la tasa de flujo másico ($kg/s$) o la tasa de flujo volumétrico ($m^3/s$) de un fluido, carga eléctrica ($A\cdot s$), densidad de flujo de masa $[kg / (m^2\cdot s)]$, y así sucesivamente.
Veremos muchos más ejemplos a lo largo de este libro. Por ahora, el punto es que cada cantidad física se puede derivar de las siete cantidades base en la Tabla 1.1, y las unidades de cada cantidad física se pueden derivar de las siete unidades base SI.
En su mayor parte, usamos unidades SI en este libro. Las unidades que no son SI se usan en algunas aplicaciones en las que son de uso común, como la medición de la temperatura en grados Celsius (°C), la medición del volumen de líquido en litros (L) y la medida de energías de partículas elementales en electronvolts (eV). Siempre que se debatan unidades que no pertenecen al SI, están vinculadas a unidades del SI a través de conversiones. Por ejemplo, 1 L es $10^{-3}\;m^3$.
Unidades de tiempo, longitud y masa: el segundo, el metro y el kilogramo
Los capítulos iniciales de este libro de texto están relacionados con mecánica, fluidos y ondas. En éstos, todas las cantidades físicas pertinentes se pueden expresar en términos de las unidades base de longitud, masa y tiempo. Por lo tanto, ahora pasamos a una discusión de estas tres unidades básicas, dejando la discusión de las otras hasta que las necesites más tarde.
El segundo
La unidad SI para el tiempo, el segundo (s), tiene una larga historia. Durante años se definió como $1/86,400$ de un día solar medio. Más recientemente, se adoptó un nuevo estándar para obtener una mayor precisión y para definir el segundo en términos de un fenómeno físico no constante o constante (porque el día solar se hace más largo como resultado de la desaceleración gradual de la rotación de la Tierra). Se puede hacer que los átomos de cesio vibren de manera constante, y estas vibraciones se pueden observar y contar fácilmente.
En 1967, el segundo fue redefinido como el tiempo requerido para que ocurran $9,192,631,770$ de estas vibraciones (Figura 1.8). Ten en cuenta que esto puede parecerte más preciso de lo que alguna vez necesitarías, pero no es así: los GPS dependen de la precisión de los relojes atómicos para poder darte indicaciones paso a paso en la superficie de la Tierra, lejos de los satélites. transmitiendo tu ubicación.

El metro
La unidad SI para la longitud es el metro (abreviado m); su definición también ha cambiado con el tiempo para volverse más precisa.
El metro se definió por primera vez en 1791 como $1/10,000,000$ de la distancia desde el ecuador hasta el Polo Norte. Esta medida se mejoró en 1889 al redefinir el metro para que fuera la distancia entre dos líneas grabadas en una barra de platino-iridio, que ahora se mantiene cerca de París. Para 1960, ya era posible definir el metro con mayor precisión en términos de la longitud de onda de la luz, por lo que nuevamente se redefinió como $1.650.763,73 $longitudes de onda de luz naranja emitidas por átomos de criptón. En 1983, el metro recibió su definición actual (en parte para una mayor precisión) a medida que la luz de distancia viaja en el vacío en $1/299,792,458$ de segundo (Figura 1.9). Este cambio se produjo después de saber que la velocidad de la luz era exactamente $299.792.458\; m/s$. La longitud del metro cambiará si la velocidad de la luz se mide algún día con mayor precisión.

El kilogramo
La unidad SI para masa es el kilogramo (abreviado kg). Se define como la masa de un cilindro de platino-iridio mantenido con el viejo estándar del metro en la Oficina Internacional de Pesos y Medidas cerca de París. Las réplicas exactas del kilogramo estándar también se guardan en el Instituto Nacional de Estándares y Tecnología (NIST) de EE.UU., Ubicado en Gaithersburg, Maryland, en las afueras de Washington DC y en otros lugares del mundo.
Los científicos del NIST están investigando actualmente dos métodos complementarios para redefinir el kilogramo (ver Figura 1.10). La determinación de todas las otras masas se puede remontar finalmente a una comparación con la masa estándar.

Prefijos métricos
Las unidades SI son parte del sistema métrico, que es conveniente para cálculos científicos y de ingeniería porque las unidades se clasifican por factores de 10.
La Tabla 1.2 enumera los prefijos y símbolos métricos utilizados para indicar varios factores de 10 en unidades SI. Por ejemplo, un centímetro es una centésima de un metro (en símbolos, $1\; cm = 10^{-2}\; m$) y un kilómetro es de mil metros ($1\; km = 10^3\; m$). De manera similar, un megagramo es un millón de gramos ($1\; Mg = 10^6\; g$), un nanosegundo es una milmillonésima de segundo ($1\; ns = 10^{-9}\; s$) y un terámetro es un billón de metros ($1\; Tm = 10^{12}\; m$).
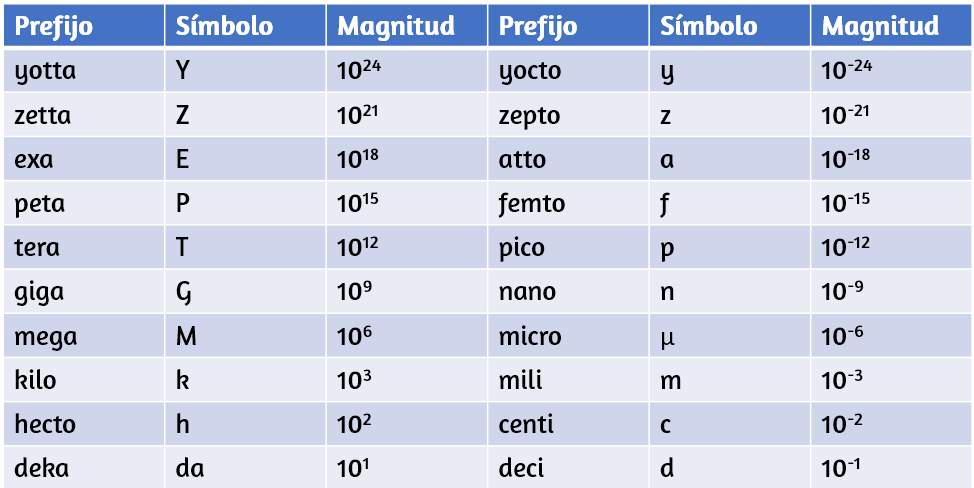
La única regla al usar prefijos métricos es que no puedes "duplicarlos". Por ejemplo, si tienes medidas en petámetros ($1\; Pm = 10^{15}\; m$), no es apropiado hablar de megagigómetros, aunque $10^6\times 10^9 = 10^{15}$. En la práctica, el único momento en que esto se vuelve un poco confuso es cuando se habla de masas. Como hemos visto, la unidad de masa SI básica es el kilogramo ($kg$), pero los prefijos métricos deben aplicarse al gramo ($g$), porque no se nos permite "ponerle un doble" a los prefijos.
Por lo tanto, mil kilogramos $(10^3\; kg)$ se escribe en megagramos $(1\; Mg)$ desde
$$10^3\;kg = 10^3\times×10^3\;g = 10^6\;g = 1\;Mg$$Por cierto, $10^3\;kg$ también se llama tonelada métrica, abreviada $t$. Esta es una de las unidades fuera del sistema SI que se considera aceptable para su uso con unidades SI. Como veremos en la siguiente sección, los sistemas métricos tienen la ventaja de que las conversiones de unidades involucran solo potencias de $10$. Hay $100 \;cm$ en $1\; m$, $1000\; m$ en $1 \;km$, y así sucesivamente. En sistemas no métricos, como el sistema inglés de unidades, las relaciones no son tan simples: hay $12$ pulgadas en $1$ pie, $5280$ pies en $1$ milla, y así sucesivamente.
Otra ventaja de los sistemas métricos es que la misma unidad se puede usar en rangos de valores extremadamente grandes simplemente escalando con un prefijo métrico apropiado. El prefijo se elige por el orden de magnitud de las cantidades físicas que se encuentran comúnmente en la tarea en cuestión. Por ejemplo, las distancias en metros son adecuadas para la construcción, mientras que las distancias en kilómetros son apropiadas para el transporte aéreo, y los nanómetros son convenientes para el diseño óptico. Con el sistema métrico no hay necesidad de inventar nuevas unidades para aplicaciones particulares. En cambio, reescalamos las unidades con las que ya estamos familiarizados.
Ejemplo 1.1
Usando prefijos métricos
Convierte la masa de $1.93 \times 10^{13}\;kg$ usando un prefijo métrico de modo que el resultado sea mayor que uno pero menor que $1000$.
Estrategia
Como no tenemos permitido "duplicar" los prefijos, primero tenemos que volver a expresar la masa en gramos reemplazando el símbolo del prefijo k por un factor de $10^3$ (consulta la Tabla 1.2). Entonces, deberíamos ver qué dos prefijos en la Tabla 1.2 están más cerca de la potencia resultante de $10$ cuando el número está escrito en notación científica. Usamos cualquiera de estos dos prefijos que nos da un número entre uno y $1000$.
Solución
Reemplazando la $k$ en kilogramos con un factor de $10^3$, encontramos que
$$1.93 \times 10^{31}\;kg = 1.93 × 10^{13}\times 10^3\;g = 1.93 × 10^{16}\;g.$$De la Tabla 1.2, vemos que $10^{16}$ está entre "peta" $(10^{15})$ y "exa" $(10^{18})$. Si usamos el prefijo "peta", entonces encontramos que $1.93 \times 10^{16}\; g = 1.93 \times 10^1\;Pg$, ya que $16 = 1 + 15$. Alternativamente, si usamos el prefijo "exa" encontramos que $1.93 × 10^{16}\;g = 1.93 \times 10^{-2}\; Eg$, ya que 1$6 = -2 + 18$. Como el problema pide el valor numérico entre uno y $1000$, usamos el prefijo "peta" y la respuesta es $19.3\; Pg$.
Verificación
Es fácil hacer tontos errores aritméticos al cambiar de un prefijo a otro, por lo que siempre es una buena idea verificar que nuestra respuesta final coincida con el número con el que comenzamos. Una forma fácil de hacerlo es poner los dos números en notación científica y contar potencias de 10, incluidas las ocultas en los prefijos. Si no cometimos un error, las potencias de 10 deberían coincidir.
En este problema, comenzamos con $1.93 \times 10^{13}\; kg$, así que tenemos $13 + 3 = 16$ potencias de $10$. Nuestra respuesta final en notación científica es $1.93 \times 10^1\; Pg$, así que tenemos $1 + 15 = 16$ potencias de $10$. Entonces, todo se comprueba. Si esta masa surgió de un cálculo, también deseamos verificar si una masa así de grande tiene sentido en el contexto del problema. Para esto, la Figura 1.4 podría ser útil.
 Comprueba tu aprendizaje 1.1
Comprueba tu aprendizaje 1.1
Puedes comprobar tu resultado usando el siguiente objeto interactivo, diseñado por Juan Guillermo Rivera B. Selecciona los prefijos en los menú correspondientes y escribe el valor a convertir en las casillas de texto.
Conversión de unidades
A menudo es necesario convertir de una unidad a otra. Por ejemplo, si está leyendo un libro de cocina europeo, algunas cantidades pueden expresarse en unidades de litros y debe convertirlas en tazas. O tal vez está leyendo las indicaciones para ir de un lugar a otro y le interesa saber cuántos kilómetros va a caminar. En este caso, puede necesitar convertir unidades de pies o millas a kilómetros.
Consideremos un ejemplo de cómo convertir unidades. Supongamos que queremos convertir $80 \;m$ a kilómetros. Lo primero que debes hacer es listar las unidades que tienes y las unidades a las que deseas convertir. En este caso, tenemos unidades en metros y queremos convertir a kilómetros. Luego, necesitamos determinar un factor de conversión que relacione metros a kilómetros. Un factor de conversión es una proporción que expresa cuántos de una unidad son iguales a otra unidad. Por ejemplo, hay $12$ pulg. en $1$ pie, $1609 m\;$ en $1$ milla, $100\; cm$ en $1 \;m$, $60 \;s$ en $1 \;min$, y así sucesivamente. Consulta las tablas de conversión para obtener una lista más completa de los factores de conversión. En este caso, sabemos que hay $1000 \;m$ en $1 \;km$. Ahora podemos configurar nuestra conversión de unidad. Escribimos las unidades que tenemos y luego las multiplicamos por el factor de conversión para que las unidades se cancelen, como se muestra: $$80\;\cancel{\textcolor{red}{m}}\times \frac{1\;km}{1000\;\cancel{\textcolor{red}{m}}} = 0.080\;km$$
Ten en cuenta que la unidad metro no deseada se cancela, dejando solo la unidad kilométrica deseada. Puedes usar este método para convertir cualquier tipo de unidad.
Ahora, la conversión de 80 m a kilómetros es simplemente el uso de un prefijo métrico, como vimos en la sección anterior, por lo que podemos obtener la misma respuesta con la misma facilidad al notar que $80 \;m = 80 \times 10^{-3}\; km = 0.080 \;km$.
Sin embargo, el uso de factores de conversión es útil cuando se convierten entre unidades que no son métricas o cuando se convierten entre unidades derivadas, como ilustran los siguientes ejemplos.
Ejemplo 1.2
Conversión de unidades no métricas a métricas
La distancia desde la universidad hasta el hogar es de $10 \;millas$ y generalmente lleva $20 \;minutos$ conducir esta distancia. Calcula la velocidad promedio en metros por segundo ($m/s$). (Nota: la velocidad promedio es la distancia recorrida dividida por el tiempo de viaje).
Estrategia
Primero calculamos la velocidad promedio usando las unidades dadas, luego podemos obtener la velocidad promedio en las unidades deseadas escogiendo los factores de conversión correctos y multiplicando por ellas. Los factores de conversión correctos son aquellos que cancelan las unidades no deseadas y dejan las unidades deseadas en su lugar. En este caso, queremos convertir millas en metros, por lo que necesitamos saber el hecho de que hay $1609 \;m$ en $1 \;mi$. También queremos convertir minutos a segundos, por lo que usamos la conversión de $60 \;s$ en $1 \;min$.
Solución
- Calcula la velocidad promedio.
- La velocidad promedio es la distancia recorrida dividida por el tiempo de viaje. (Toma esta definición como dada por ahora. La velocidad promedio y otros conceptos de movimiento se tratarán en capítulos posteriores). En forma de ecuación,
- Sustituye los valores dados por distancia y tiempo:
- Convierte millas por minuto en metros por segundo multiplicando por el factor de conversión que cancela millas y cancela los metros, y también por el factor de conversión que cancela los minutos y deja segundos: $$0.50 \frac{\textcolor{red}{\cancel{mi}}}{\textcolor{lightgreen}{\cancel{min}}}\frac{1609}{1\;\textcolor{red}{\cancel{mi}}}\times \frac{1\;\textcolor{lightgreen}{\cancel{min}}}{60\;s} = \frac{(0.50)(1609)}{60\;s}m/s = 13 m/s$$
Verificación
Verifica la respuesta de las siguientes maneras:
- Asegúrate que las unidades en la conversión se cancelan correctamente. Si el factor de conversión de la unidad se escribió al revés, las unidades no se cancelan correctamente en la ecuación. Vemos que las "millas" en el numerador en $0.50 \;mi/min$ cancela la "milla" en el denominador en el primer factor de conversión. Además, el "min" en el denominador en $0.50 \;mi/min$ cancela el "min" en el numerador en el segundo factor de conversión.
- Verifica que las unidades de la respuesta final sean las unidades deseadas. El problema nos pedía que resolviéramos la velocidad promedio en unidades de metros por segundo y, después de las cancelaciones, las únicas unidades que quedan son un metro (m) en el numerador y un segundo (s) en el denominador, por lo que efectivamente las hemos obtenido unidades.
 Comprueba tu aprendizaje 1.2
Comprueba tu aprendizaje 1.2
Ejemplo 1.3
Convertir entre unidades métricas
La densidad del hierro es $7.86 \;g/cm^3$ en condiciones estándar. Convierte ésto a $kg/m^3$.
Estrategia
Necesitamos convertir gramos a kilogramos y centímetros cúbicos a metros cúbicos. Los factores de conversión que necesitamos son $1\;kg = 10^3\;g$ y $1\;cm = 10^{-2}\;m$. Sin embargo, estamos tratando con centímetros cúbicos ($cm^3 = cm \times cm \times cm$), por lo que tenemos que usar el factor de la segunda conversión tres veces (es decir, tenemos que ponerlo en el cubo).
La idea es aún multiplicar por los factores de conversión de tal forma que cancelen las unidades de las que queremos deshacernos e introduzcan las unidades que queremos conservar.
Solución
$$\begin{split} 7.86\frac{\textcolor{red}{\cancel{g}}} {\textcolor{lightblue}{\cancel{cm^3}}} \times \frac{kg}{10^3\textcolor{red}{\cancel{g}}} \times \bigg(\frac{\textcolor{lightblue}{\cancel{cm}}}{10^{-2}m} \bigg)&= \frac{7.86}{10^3\times 10^{-6}}kg/m^3\\ &= 7.86\times 10^3kg/m^3 \end{split}$$Verificación
Recuerda, siempre es importante verificar la respuesta.
- Asegúrate de cancelar las unidades en la conversión de la unidad correctamente. Vemos que el gramo ("g") en el numerador en $7.86\; g/cm^3$ cancela la "g" en el denominador en el primer factor de conversión. Además, los tres factores de "cm" en el denominador en $7.86 \;g/cm^3$ se cancelan con los tres factores de "cm" en el numerador que obtenemos al dividir el segundo factor de conversión.
- Verifica que las unidades de la respuesta final sean las unidades deseadas. El problema nos pidió que convirtiéramos a kilogramos por metro cúbico. Después de las cancelaciones que acabamos de describir, vemos que las únicas unidades que nos quedan son "kg" en el numerador y tres factores de "m" en el denominador (es decir, un factor de "m" en cubos o "$m^3$"). Por lo tanto, las unidades en la respuesta final son correctas.
 Comprueba tu aprendizaje 1.3
Comprueba tu aprendizaje 1.3
Las conversiones de unidades pueden no parecer muy interesantes, pero no hacerlas puede ser costoso. Un ejemplo famoso de esta situación fue visto con Mars Climate Orbiter. Esta sonda fue lanzada por la NASA el 11 de diciembre de 1998.
El 23 de septiembre de 1999, mientras intentaba guiar la sonda hacia su órbita planeada alrededor de Marte, la NASA perdió el contacto con ella. Investigaciones posteriores mostraron que un software llamado SM_FORCES (o "fuerzas pequeñas") registraba los datos de rendimiento del propulsor en las unidades inglesas de libra-segundos (lb-s). Sin embargo, otras piezas de software que utilizaron estos valores para las correcciones de los cursos esperaban que se grabasen en las unidades SI de newton-segundos (N-s), tal como se establece en los protocolos de la interfaz del software. Este error provocó que la sonda siguiera una trayectoria muy diferente de la que la NASA pensó que estaba siguiendo, lo que probablemente causó que la sonda se quemara en la atmósfera marciana o se disparara al espacio. Esta falla en prestar atención a las conversiones de unidades cuesta cientos de millones de dólares, sin mencionar todo el tiempo invertido por los científicos e ingenieros que trabajaron en el proyecto.
 Comprueba tu aprendizaje 1.4
Comprueba tu aprendizaje 1.4
Aplicativo para conversión de unidades
Existe una gran variedad de aplicativos gratuitos, en línea, para realizar conversiones. Uno de ellos es Js Measurements Converters, que hemos modificado en la siguiente página. Con dicho aplicativo, puedes verificar tus resultados en los ejercicios propuestos. Por ejemplo, si deseamos convertir $7.86\; g/cm^3$ a $kg/m^3$, con el aplicativo hallamos el factor de conversión, seleccionado unidades de densidad, encontrando que el factor de conversión de $1\; g/cm^3$ a $kg/m^3$ es $1000$, es decir, $7.86 \;g/cm^3 = 7860 \;kg/m^3$. Ahora, haz tu la prueba:
Análisis dimensional
La dimensión de cualquier cantidad física expresa su dependencia de las cantidades base como producto de símbolos (o potencias de símbolos), que representan las cantidades base. La Tabla 1.3 enumera las cantidades base y los símbolos utilizados para su dimensión. Por ejemplo, se dice que una medida de longitud tiene una dimensión L o L1, una medición de masa tiene una dimensión M o M1, y una medición de tiempo tiene una dimensión T o T1. Como las unidades, las dimensiones obedecen las reglas del álgebra. Por lo tanto, el área es el producto de dos longitudes, por lo que tiene una dimensión L2 o una longitud al cuadrado. Del mismo modo, el volumen es el producto de tres longitudes y tiene una dimensión L3 o longitud al cubo. La velocidad tiene una longitud de dimensión en el tiempo, L/T o LT-1. La densidad de masa volumétrica tiene una dimensión M/L3 o ML-3, o masa sobre la longitud al cubo. En general, la dimensión de cualquier cantidad física se puede escribir como LaMbTcIdΘeNfJg para algunas potencias a, b, c, d, e, f, y g. Podemos escribir las dimensiones de una longitud en esta forma con a = 1 y las seis potencias restantes son todas iguales a cero: L1 = L1M0T0I0Θ0N0J0. Cualquier cantidad con una dimensión que se pueda escribir de modo que las siete potencias sean cero (es decir, su dimensión es L0M0T0I0Θ0N0J0) se denomina adimensional (o a veces "de dimensión 1", porque cualquier elemento elevado a la potencia cero es uno). Los físicos a menudo llaman cantidades absolutas a los números puros.
Los físicos a menudo usan corchetes alrededor del símbolo para una cantidad física para representar las dimensiones de esa cantidad. Por ejemplo, si r es el radio de un cilindro y h es su altura, entonces escribimos [r] = L y [h] = L para indicar que las dimensiones del radio y la altura son ambos de longitud, o L.
De forma similar, si usamos el símbolo A para el área de superficie de un cilindro y V para su volumen, entonces [A] = L2 y [V] = L3. Si usamos el símbolo m para la masa del cilindro y ρ para la densidad del material del que está hecho el cilindro, entonces [m] = M y [ρ] = ML-3.
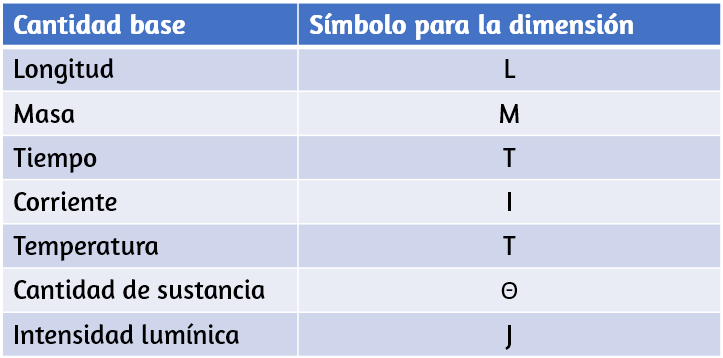
La importancia del concepto de dimensión surge del hecho de que cualquier ecuación matemática que relacione cantidades físicas debe ser dimensionalmente consistente, lo que significa que la ecuación debe obedecer a las siguientes reglas:
- Cada término en una expresión debe tener las mismas dimensiones; no tiene sentido sumar o restar cantidades de diferente dimensión (piense en el viejo dicho: "No puede sumar manzanas y naranjas"). En particular, las expresiones en cada lado de la igualdad en una ecuación deben tener las mismas dimensiones.
- Los argumentos de cualquiera de las funciones matemáticas estándar tales como funciones trigonométricas (como seno y coseno), logaritmos o funciones exponenciales que aparecen en la ecuación deben ser adimensionales. Estas funciones requieren números puros como entradas y dan números puros como salidas.
Si se viola cualquiera de estas reglas, una ecuación no es dimensionalmente coherente y no puede ser una declaración correcta de la ley física. Este simple hecho se puede usar para verificar errores tipográficos o de álgebra, para ayudar a recordar las diversas leyes de la física e incluso para sugerir la forma que las nuevas leyes de la física podrían tomar. Este último uso de las dimensiones está más allá del alcance de este texto, pero es algo que indudablemente aprenderás más adelante en tu carrera académica.
Ejemplo 1.4
Usar dimensiones para recordar una ecuación
Supongamos que necesitamos la fórmula para el área de un círculo para algún cálculo. Al igual que muchas personas que aprendieron geometría hace mucho tiempo para recordar con certeza, dos expresiones pueden aparecer en nuestra mente cuando pensamos en círculos: $\pi r^2$ y $2\pi r$. Una expresión es la circunferencia de un círculo de radio $r$ y la otra es su área. Pero, ¿cuál es cuál?
Estrategia
Una estrategia natural es consultarlo, pero ésto podría tomar tiempo para encontrar información de una fuente acreditada. Además, incluso si pensamos que la fuente es respetable, no debemos confiar en todo lo que leemos.
Es bueno tener una forma de verificarlo solo por pensarlo. Además, podríamos estar en una situación en la que no podamos buscar las cosas (como durante una prueba). Por lo tanto, la estrategia es encontrar las dimensiones de ambas expresiones haciendo uso del hecho de que las dimensiones siguen las reglas del álgebra. Si cualquiera de las expresiones no tiene las mismas dimensiones que el área, entonces posiblemente no sea la ecuación correcta para el área de un círculo.
Solución
Sabemos que la dimensión del área es L2. Ahora, la dimensión de la expresión $\pi r^2$ es
$$\text{[}\pi r^2\text{]} = \text{[}\pi\text{]}\cdot\text{[}r\text{]}^2 = 1\cdot\text{L}^2 = \text{L}^2$$ya que la constante $\pi$ es un número puro y el radio $r$ es una longitud. Por lo tanto, $\pi r^2$ tiene la dimensión del área. Del mismo modo, la dimensión de la expresión $2\pi r$ es
$$\text{[}2\pi r\text{]} = \text{[}2\text{]}\cdot \text{[}\pi\text{]} \cdot \text{[}r\text{]} =1\cdot 1\cdot \text{L} = \text{L}$$ya que las constantes $2$ y $\pi$ son adimensionales y el radio $r$ es una longitud. Vemos que $2\pi r$ tiene la dimensión de longitud, lo que significa que no puede ser un área. Descartamos $2\pi r$ porque no es dimensionalmente consistente con ser un área. Vemos que $\pi r^2$ es dimensionalmente consistente con ser un área, por lo que si tenemos que elegir entre estas dos expresiones, $\pi r^2$ es la que hay que elegir.
Verificación
Esto puede parecer un ejemplo tonto, pero las ideas son muy generales.
Mientras sepamos las dimensiones de las cantidades físicas individuales que aparecen en una ecuación, podemos verificar si la ecuación es dimensionalmente consistente. Por otro lado, sabiendo que las ecuaciones verdaderas son dimensionalmente consistentes, podemos unir las expresiones de nuestras memorias imperfectas con las cantidades para las cuales podrían ser expresiones. Hacer esto no nos ayudará a recordar los factores adimensionales que aparecen en las ecuaciones (por ejemplo, si ha confundido accidentalmente las dos expresiones del ejemplo en $2\pi r^2$, entonces el análisis dimensional no es de ayuda), pero nos ayuda a recordar la correcta forma de las ecuaciones.
 Comprueba tu aprendizaje 1.5
Comprueba tu aprendizaje 1.5
Ejemplo 1.5
Comprobación de ecuaciones para la consistencia dimensional
Considera las cantidades físicas $s, v, a$ y $t$ con dimensiones [$s$] = L, [$v$] = LT-1, [$a$] = LT-2, y [$t$] = T. Determina si cada una de las siguientes ecuaciones son dimensionalmente consistentes: (a) $s = vt + 0.5a^2$; (b) $s = vt^2 + 0.5at$; y (c) $v = sen (at^2/s)$.
Estrategia
Por la definición de consistencia dimensional, necesitamos verificar que cada término en una ecuación dada tenga las mismas dimensiones que los otros términos en esa ecuación y que los argumentos de cualquier función matemática estándar sean adimensionales.
- (a) No hay funciones trigonométricas, logarítmicas o exponenciales de las que preocuparse en esta ecuación, por lo que solo debemos observar las dimensiones de cada término que aparece en la ecuación. Hay tres términos, uno en la expresión izquierda y dos en la expresión de la derecha, por lo que observamos cada uno a su vez:
[$s$] = L
[$vt$] = [$v$]·[$t$] = LT−1· T = LT0 = L
[$0.5at^2$] = [a]·[t]2 = LT−2·T2 = LT0 = L.
Los tres términos tienen la misma dimensión, por lo que esta ecuación es dimensionalmente consistente - (b) De nuevo, no hay funciones trigonométricas, exponenciales o logarítmicas, por lo que solo tenemos que mirar las dimensiones de cada uno de los tres términos que aparecen en la ecuación:
[$s$] = L
[$vt^2$] = [$v$]·[$t$]2 = LT-1·T2 = LT
[$at$] = [$a$]·[$t$] = LT-2·T = LT-1
Ninguno de los tres términos tiene la misma dimensión que cualquier otro, por lo que está tan lejos de ser lo más coherente posible. El término técnico para una ecuación como esta no tiene sentido.
- (c) Esta ecuación tiene una función trigonométrica, por lo que primero debemos verificar que el argumento de la función seno sea adimensional: $$\bigg[\frac{at^2}{s}\bigg] = \frac{\text{[}a\text{]}\cdot \text{[}t\text{]}^2}{\text{[} s\text{]}} = \frac{\text{LT}^2\cdot \text{T}^2}{\text{L}} = \frac{\text{L}}{\text{L}} = 1$$ El argumento es adimensional. Hasta aquí todo bien. Ahora necesitamos verificar las dimensiones de cada uno de los dos términos (es decir, la expresión izquierda y la expresión derecha) en la ecuación: $$[v] = \text{LT}^{-1}\\ \bigg[sen\Big(\frac{at^2}{s}\Big)\bigg] = 1$$ Los dos términos tienen diferentes dimensiones, lo que significa que la ecuación no es dimensionalmente consistente. Esta ecuación es otro ejemplo de "tonterías".
Verificación
Si confiamos en las personas, este tipo de controles dimensionales puede parecer innecesario. Pero, tenga la seguridad, cualquier libro de texto sobre un tema cuantitativo como la física (incluido éste) casi con seguridad contiene algunas ecuaciones con errores tipográficos. Comprobar las ecuaciones de forma rutinaria mediante análisis dimensional nos ahorra la vergüenza de usar una ecuación incorrecta.
Además, verificar las dimensiones de una ecuación que obtenemos a través de la manipulación algebraica es una gran manera de asegurarnos de que no cometimos un error (o detectar un error, si hicimos uno).
 Comprueba tu aprendizaje 1.6
Comprueba tu aprendizaje 1.6
Otro punto que debe mencionarse es el efecto de las operaciones de cálculo en las dimensiones. Hemos visto que las dimensiones obedecen las reglas del álgebra, al igual que las unidades, pero ¿qué sucede cuando tomamos la derivada de una cantidad física con respecto a otra o integramos una cantidad física sobre otra? La derivada de una función es solo la pendiente de la línea tangente a su gráfico y las pendientes son razones, por lo que para las cantidades físicas $v$ y $t$, tenemos que la dimensión de la derivada de $v$ con respecto a $t$ es solo la relación de la dimensión de $v$ sobre el de $t$:
$$\bigg[\frac{dv}{dt}\bigg] = \frac{[v]}{[t]}$$Igualmente, dado que las integrales son solo sumas de productos, la dimensión de la integral de $v$ con respecto a $t$ es simplemente la dimensión de v por la dimensión de $t$:
$$\bigg[\int vdt\bigg] = [v]\cdot [t]$$Las reglas análogas son válidas para las unidades de cantidades físicas derivadas de otras cantidades por integración o diferenciación.
Estimaciones y cálculos de Fermi
En muchas ocasiones, los físicos, otros científicos e ingenieros necesitan hacer estimaciones para una cantidad en particular. Otros términos utilizados a veces son estimaciones aproximadas, aproximaciones de orden de magnitud, cálculos de respaldo de la envolvente o cálculos de FermiEl físico Enrico Fermi era famoso por su capacidad para estimar diversos tipos de datos con sorprendente precisión.. ¿Encajará ese equipo en la parte trasera del automóvil o necesitamos alquilar un camión? ¿Cuánto tiempo llevará esta descarga? ¿Qué tan grande será la corriente en este circuito cuando esté encendido? ¿Cuántas casas podría una planta de energía soportar? Ten en cuenta que estimar no significa adivinar un número o una fórmula al azar. Más bien, la estimación significa usar la experiencia previa y un razonamiento físico sólido para llegar a una idea aproximada del valor de una cantidad. Debido a que el proceso de determinación de una aproximación confiable generalmente implica la identificación de principios físicos correctos y una buena suposición acerca de las variables relevantes, la estimación es muy útil para desarrollar la intuición física. Las estimaciones también nos permiten realizar "controles de cordura" sobre los cálculos o las propuestas de políticas al ayudarnos a descartar ciertos escenarios o números poco realistas. Nos permiten desafiar a otros (así como a nosotros mismos) en nuestros esfuerzos por aprender verdades sobre el mundo.
Muchas estimaciones se basan en fórmulas en las cuales las cantidades de entrada son conocidas solo con una precisión limitada. A medida que desarrollas habilidades de resolución de problemas de física, también desarrollarás habilidades para estimar. Desarrollas estas habilidades pensando más cuantitativamente y estando dispuesto a asumir riesgos.
Como con cualquier habilidad, la experiencia ayuda. La familiaridad con las dimensiones y las unidades también ayudan.
Para avanzar en la estimación, debes tener algunas ideas claras sobre cómo se relacionan las variables. Las siguientes estrategias pueden ayudarte a practicar el arte de la estimación:
- Al estimar longitudes, recuerde que cualquier cosa puede ser una regla. Por lo tanto, imagina dividir una cosa grande en cosas más pequeñas, estimar la longitud de una de las cosas más pequeñas y multiplicar para obtener la longitud de la cosa grande. Por ejemplo, para estimar la altura de un edificio, primero cuenta cuántos pisos tiene. Luego, calcula qué tan grande es un solo piso al imaginar cuántas personas tendrían que pararse sobre los hombros para llegar al techo. Por último, estima la altura de una persona. El producto de estas tres estimaciones es tu estimación de la altura del edificio. Es útil haber memorizado algunas escalas de longitud relevantes para los tipos de problemas que te encuentras resolviendo. Por ejemplo, conocer algunas escalas de longitud en la Figura 1.4 puede ser útil. A veces también ayuda a hacer esto en reversa, es decir, para estimar la longitud de una cosa pequeña, imagina que un grupo de ellos hace una cosa más grande. Por ejemplo, para estimar el grosor de una hoja de papel, estima el grosor de una pila de papel y luego divide por el número de páginas en la pila. Estas mismas estrategias de dividir cosas grandes en cosas más pequeñas o agregar cosas más pequeñas en una cosa más grande a veces se pueden usar para estimar otras cantidades físicas, como las masas y los tiempos.
- Obten áreas y volúmenes a partir de longitudes. Al tratar con un área o un volumen de un objeto complejo, introduce un modelo simple del objeto, como una esfera o una caja.
- Luego, primero calcula las dimensiones lineales (como el radio de la esfera o la longitud, el ancho y la altura de la caja) y utiliza sus estimaciones para obtener el volumen o el área a partir de las fórmulas geométricas estándar. Si tienes una estimación del área o volumen de un objeto, también puedes hacer lo contrario; es decir, usa fórmulas geométricas estándar para obtener una estimación de sus dimensiones lineales.
- Obten masas de volúmenes y densidades. Al estimar masas de objetos, primero puede ayudar a estimar su volumen y luego estimar su masa a partir de una estimación aproximada de su densidad promedio (recuerda, la densidad tiene como dimensión la masa sobre la longitud al cubo, entonces la masa es densidad por volumen). Para esto, es útil recordar que la densidad del aire es de alrededor de $1 \;kg/m^3$, la densidad del agua es de $10^3\; kg/m^3$ y los sólidos más densos alcanzan un máximo de alrededor de $10^4\; kg/m^3$. Preguntándote si un objeto flota o se hunde en el aire o en el agua, obtienes una estimación aproximada de su densidad. También puedes hacer esto al revés; si tienes una estimación de la masa de un objeto y su densidad, puedes usarlos para obtener una estimación de su volumen.
- Si todo lo demás falla. Para cantidades físicas para las que no tienes mucha intuición, a veces lo mejor que puedes hacer es pensar algo así como: Bueno, debe ser más grande que esto y más pequeño que eso. Por ejemplo, supongamos que necesitas estimar la masa de un alce. Tal vez tengas mucha experiencia con alces y conozcas su masa media de forma espontánea. Si es así, genial. Pero para la mayoría de las personas, lo mejor que pueden hacer es pensar algo así como: debe ser más grande que una persona ($10^2\; kg$) y menos que un automóvil ($10^3\; kg$).
- Si necesitas un solo número para un cálculo posterior, puedes tomar la media geométrica del límite superior e inferior, es decir, multiplicarlos juntos y luego tomar la raíz cuadrada. Para el ejemplo de masa de alce, esto sería $$(10^2\times 10^3)^{0.5} = 10^{2.5} = 10^{0.5}\times 10^2\approx 3\times 10^2\; kg$$ Cuanto más ajustados sean los límites, mejor. Además, no hay reglas irrompibles en lo que respecta a la estimación. Si crees que el valor de la cantidad es probable que esté más cerca del límite superior que el límite inferior, entonces puedes querer aumentar su estimación de la media geométrica en un orden o dos de magnitud.
- No es necesario ir más allá de una cifra significativa al hacer cálculos para obtener un estimado. En la mayoría de los casos, el orden de magnitud es suficientemente bueno. El objetivo es solo obtener la figura del estadio, así que mantenga la aritmética lo más simple posible.
- Pregúntate: ¿tiene sentido esto? Por último, verifica si tu respuesta es razonable. ¿Cómo se compara con los valores de otras cantidades con las mismas dimensiones que tu ya sabes o puedes buscar fácilmente? Si obtienes alguna respuesta absurda (por ejemplo, si estima que la masa del Océano Atlántico es más grande que la masa de la Tierra, o que algún lapso de tiempo es más largo que la edad del universo), primero verifica si tus unidades son correctas. Luego, verifica los errores aritméticos. Luego, reconsidere la lógica que usaste para llegar a tu respuesta. Si todo se comprueba, es posible que hayas demostrado que una nueva idea ingeniosa es en realidad falsa.
Ejemplo 1.6
Masa de los océanos de la tierra
Estima la masa total de los océanos en la Tierra.
Estrategia
Sabemos que la densidad del agua es aproximadamente $10^2\; kg/m^3$, por lo que comenzamos con el consejo de "obtener masas a partir de densidades y volúmenes". Por lo tanto, necesitamos estimar el volumen de los océanos del planeta. Usando el consejo de "obtener áreas y volúmenes a partir de longitudes", podemos estimar el volumen de los océanos como el área de la superficie por la profundidad promedio, o $V = AD$.
Conocemos el diámetro de la Tierra de la Figura 1.4 y sabemos que la mayor parte de la superficie de la Tierra está cubierta de agua, por lo que podemos estimar que el área de la superficie de los océanos es aproximadamente igual a la superficie del planeta. Siguiendo el consejo de "obtener áreas y volúmenes de longitudes" de nuevo, podemos aproximar a la Tierra como una esfera y usar la fórmula para el área de superficie de una esfera de diámetro d, es decir, $A = \pi;d^2$, para estimar el área de la superficie de los océanos. Ahora, solo tenemos que estimar la profundidad promedio de los océanos. Sabemos que los puntos más profundos del océano están a unos 10 km y que no es raro que el océano esté a más de 1 km, por lo que la profundidad promedio puede estar alrededor de ($10^3\times 10^4)^{0.5}\approx 3 \times 10^3\; m$.
Ahora, sólo tenemos que poner todo junto.
Solución
Estimamos que el área de superficie de la Tierra (y por lo tanto el área de la superficie de los océanos de la Tierra) es aproximadamente
$A = \pi d^2 = \pi (10^7\; m)^2\approx 3 \times 10^{14}\; m^2$.
$A = \pi d^2 = \pi (10^7\; m)^2 \approx 3 \times 10^{14}\; m^2$.
A continuación, utilizando nuestra estimación de profundidad promedio de $D = 3 \times 10^3\; m$, que se obtuvo mediante el límite, estimamos que el volumen de los océanos de la Tierra será
$V = AD = (3 \times 10^{14}\;m^2)(3 \times 10^3\;m) = 9 \times 10^{17}\; m^3$.
$V = AD = (3 \times 10^{14}\; m^2)(3 \times 10^3\; m) = 9 \times 10^{17}\; m^3$.
Por último, estimamos que la masa de los océanos del mundo será
Por lo tanto, estimamos que el orden de magnitud de la masa de los océanos del planeta es $10^{21}\; kg$.
Verificación
Para verificar nuestra respuesta lo mejor que podamos, primero debemos responder a la pregunta: ¿Tiene sentido esto? De la Figura 1.4, vemos que la masa de la atmósfera de la Tierra es del orden de $10^{19}\; kg$ y la masa de la Tierra es del orden de $10^{25}\; kg$. Es tranquilizador que nuestra estimación de $10^{21}\; kg$ para la masa de los océanos de la Tierra se encuentre entre estos dos. Entonces, sí, parece tener sentido.
Ocurre que hicimos una búsqueda en la Web de "masa de océanos" y los resultados de búsqueda principales indicaron $1.4 \times 10^{21}\; kg$, que es del mismo orden de magnitud que nuestro cálculo. Ahora, en lugar de tener que confiar ciegamente en quien primero colocó ese número en un sitio web (la mayoría de los otros sitios probablemente solo lo copiaron, después de todo), podemos tener un poco más de confianza en él.
 Comprueba tu aprendizaje 1.7
Comprueba tu aprendizaje 1.7
Cifras significativas
La Figura 1.11 muestra dos instrumentos utilizados para medir la masa de un objeto. La báscula digital ha reemplazado, en su mayoría, a la balanza de doble bandeja en los laboratorios de física, porque brinda mediciones más precisas.
¿Pero a qué nos referimos exactamente por precisión? ¿No son lo mismo? En esta sección, examinamos en detalle el proceso de calcular y reportar una medición.

Exactitud y precisión de una medición
La ciencia se basa en la observación y el experimento, es decir, en las mediciones. La exactitud es qué tan cerca está una medición del valor de referencia aceptado para esa medición. Por ejemplo, supongamos que queremos medir la longitud del papel de la impresora estándar. El paquete en el que compramos el papel indica que mide 11.0 pulgadas de largo. Luego medimos la longitud del papel tres veces y obtenemos las siguientes medidas: $11.1\; pulg., 11.2\; pulg$ y $10.9\; pulg$. Estas mediciones son bastante precisas porque están muy cerca del valor de referencia de $11.0\; pulg$. Por contraste, si obtuvimos una medida de $12$ pulgadas, nuestra medición no sería muy precisa. Ten en cuenta que el concepto de exactitud requiere que se proporcione un valor de referencia aceptado.
La precisión de las mediciones se refiere a cuán cerca está el acuerdo entre mediciones independientes repetidas (que se repiten en las mismas condiciones). Considere el ejemplo de las medidas de papel. La precisión de las mediciones se refiere a la propagación de los valores medidos. Una forma de analizar la precisión de las mediciones es determinar el rango o diferencia entre los valores medidos más bajos y los más altos. En este caso, el valor más bajo fue $10.9$ pulgadas y el valor más alto fue $11.2$ pulgadas. Por lo tanto, los valores medidos se desviaron unos de otros, a lo sumo, $0.3$ pulgadas. Estas mediciones fueron relativamente precisas porque no variaron demasiado en valor. Sin embargo, si los valores medidos hubieran sido $10.9\; pulg., 11.1\; pulg.$ y $11.9\; pulg.$, entonces las mediciones no serían muy precisas porque habría una variación significativa de una medición a otra. Ten en cuenta que el concepto de precisión solo depende de las medidas reales adquiridas y no depende de un valor de referencia aceptado.
Las medidas en el ejemplo de papel son precisas, pero en algunos casos, las mediciones son precisas pero no exactas, o son exactas pero no precisas.
Consideremos un ejemplo de un GPS que intenta ubicar la posición de un restaurante en una ciudad. Piense en la ubicación del restaurante como existente en el centro de un objetivo y piense en cada intento del GPS de ubicar el restaurante como un punto negro. En la Figura 1.12 (a), vemos que las mediciones de GPS están separadas unas de otras, pero todas están relativamente cerca de la ubicación real del restaurante en el centro del objetivo. Esto indica un sistema de medición de alta exactitud y baja precisión. Sin embargo, en la Figura 1.12 (b), las mediciones de GPS se concentran bastante cerca unas de otras, pero están lejos de la ubicación objetivo. Esto indica un sistema de medición de alta precisión y baja exactitud.
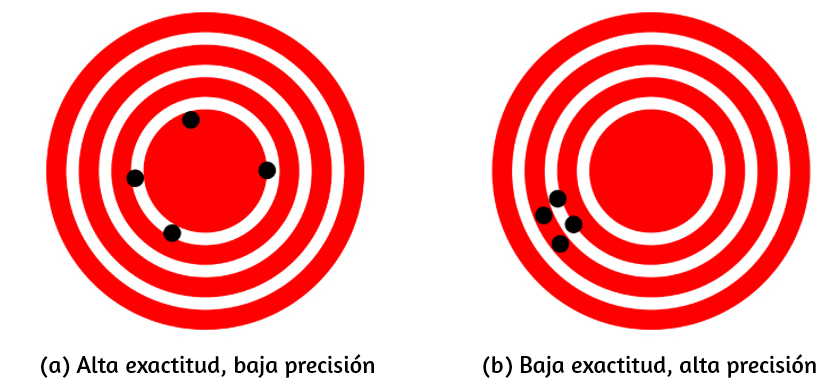
Exactitud, Precisión, Incertidumbre y Discrepancia
La precisión de un sistema de medición está relacionada con la incertidumbre en las mediciones, mientras que la exactitud está relacionada con la discrepancia con respecto al valor de referencia aceptado. La incertidumbre es una medida cuantitativa de cuánto se desvían los valores medidos el uno del otro. Existen muchos métodos diferentes para calcular la incertidumbre, cada uno de los cuales es apropiado para diferentes situaciones. Algunos ejemplos incluyen tomar el rango (es decir, el más grande menos el más pequeño) o encontrar la desviación estándar de las mediciones. La discrepancia (o "error de medición") es la diferencia entre el valor medido y un valor estándar o esperado dado. Si las medidas no son muy precisas, entonces la incertidumbre de los valores es alta. Si las medidas no son muy exactas, entonces la discrepancia de los valores es alta.
Recuerda nuestro ejemplo de medir la longitud del papel; obtuvimos medidas de $11.1\; pulg., 11.2 \;pulg.$ y $10.9\; pulg.$, y el valor aceptado fue $11.0 \;pulg.$ Podríamos promediar las tres mediciones para decir que nuestra mejor estimación es $11.1 \;pulg.$; en este caso, nuestra discrepancia es $11.1 - 11.0 = 0.1\; pulg.$, que proporciona una medida cuantitativa de exactitud. Podríamos calcular la incertidumbre en nuestra mejor estimación utilizando el rango de nuestros valores medidos: $0.3 \;pulg.$ Entonces diríamos que la longitud del papel es $11.1 \;pulg.$ más o menos $0.3\;pulg.$ La incertidumbre en una medición $A$, es a menudo denotado como $\delta A$ (leer "delta A"), por lo que el resultado de la medición se registraría como $A \pm \delta A$. Volviendo a nuestro ejemplo en papel, la longitud medida del papel podría expresarse como $11.1 \pm 0.3 \; pulg.$ Dado que la discrepancia de $0.1 \; pulg$ es menor que la incertidumbre de $0.3 \;pulg.$, podríamos decir que el valor medido concuerda con el valor de referencia aceptado dentro de la incertidumbre experimental.
Algunos factores que contribuyen a la incertidumbre en una medición son los siguientes:
- Limitaciones del dispositivo de medición
- La habilidad de la persona que toma la medida
- Irregularidades en el objeto que se mide
- Cualquier otro factor que afecte el resultado (altamente dependiente de la situación)
En nuestro ejemplo, los factores que contribuyen a la incertidumbre podrían ser que la división más pequeña en la regla sea $1/16 \;pulg.$, La persona que usa la regla tiene mala vista, la regla está desgastada en un extremo, o una de las caras del papel es un poco más largo que el otro.
En cualquier caso, la incertidumbre en una medición debe calcularse para cuantificar su precisión. Si se conoce un valor de referencia, tiene sentido calcular la discrepancia y cuantificar su exactitud.
Porcentaje de incertidumbre
Otro método para expresar la incertidumbre es como un porcentaje del valor medido. Si una medida $A$ se expresa con incertidumbre $\delta A$, la incertidumbre porcentual se define como
$$\text{Porcentaje de incertidumbre} = \frac{\delta A}{A}\times 100\%$$Ejemplo 1.7
Cálculo del porcentaje de incertidumbre: una bolsa de manzanas
Una tienda de comestibles vende bolsas de manzanas de $5 \;lb$.
Digamos que compramos cuatro bolsas durante el transcurso de un mes y pesamos las bolsas cada vez. Obtenemos las siguientes medidas:
- Peso de la semana 1: 4.8 lb
- Peso de la semana 2: 5.3 lb
- Peso de la semana 3: 4.9 lb
- Peso de la semana 4: 5.4 libras
Luego determinamos que el peso promedio de la bolsa de manzanas de $5\; lb$ es $5.1 \pm 0.2\; lb$. ¿Cuál es el porcentaje de incertidumbre del peso de la bolsa?
Estrategia
Primero, observa que el valor promedio del peso de la bolsa, A, es $5.1 \;lb.$
La incertidumbre en este valor, $\delta A$, es $0.2\; lb$. Podemos usar la siguiente ecuación para determinar el porcentaje de incertidumbre del peso:
$$\text{Porcentaje de incertidumbre} = \frac{\delta A}{A}\times 100\%\tag{1.1}$$Solución
Sustituye los valores en la ecuación:
$$\begin{split} \text{Porcentaje de incertidumbre} &= \frac{\delta A}{A}\times 100\%\\ &= \frac{0.2\; lb}{5.1\; lb}\times 100\% = 3.9\% \approx 4\% \end{split}$$Verificación
Podemos concluir que el peso promedio de una bolsa de manzanas en esta tienda es de $5.1\; lb \pm 4\%$. Observa que la incertidumbre porcentual es adimensional porque las unidades de peso en $\delta A = 0.2 \;lb$ cancelaron aquellas en $A = 5.1 \;lb$ cuando tomamos la razón.
 Comprueba tu aprendizaje 1.8
Comprueba tu aprendizaje 1.8
Incertidumbres en los cálculos
La incertidumbre existe en cualquier cosa calculada a partir de cantidades medidas. Por ejemplo, el área de un piso calculada a partir de mediciones de su longitud y ancho tiene una incertidumbre porque la longitud y el ancho tienen incertidumbres. ¿Qué tan grande es la incertidumbre en algo que se calcula por multiplicación o división? Si las mediciones que entran en el cálculo tienen pequeñas incertidumbres (un pequeño porcentaje o menos), entonces el método de agregar porcentajes se puede usar para la multiplicación o división.
Este método indica que la incertidumbre porcentual en una cantidad calculada por multiplicación o división es la suma de las incertidumbres porcentuales en la información utilizada para hacer el cálculo. Por ejemplo, si un piso tiene una longitud de $4.00 \;m$ y un ancho de $3.00 \;m$, con incertidumbres del $2\%$ y $1\%$, respectivamente, entonces el área del piso es de $12.0 \;m^2$ y tiene una incertidumbre del $3\;\%$ (Expresado como un área, esto es $0.36 m^2 [12.0 \;m^2\times 0.03]$, que redondeamos a $0.4 \;m^2$ ya que el área del piso se da a una décima de metro cuadrado).
Precisión de herramientas de medición y cifras significativas
Un factor importante en la precisión de las mediciones involucra la precisión de la herramienta de medición. En general, una herramienta de medición precisa es aquella que puede medir valores en incrementos muy pequeños. Por ejemplo, una regla estándar puede medir la longitud al milímetro más cercano, mientras que una pinza puede medir la longitud al milímetro más cercano. El calibrador es una herramienta de medición más precisa porque puede medir diferencias extremadamente pequeñas en longitud. Cuanto más precisa sea la herramienta de medición, más precisas serán las mediciones.
Cuando expresamos valores medidos, solo podemos enumerar tantos dígitos como medimos inicialmente con nuestra herramienta de medición. Por ejemplo, si usamos una regla estándar para medir la longitud de un palo, podemos medirlo en $36.7 \;cm$. No podemos expresar este valor como $36,71 \;cm$ porque nuestra herramienta de medición no es lo suficientemente precisa como para medir una centésima de centímetro. Cabe señalar que el último dígito en un valor medido ha sido estimado de alguna manera por la persona que realiza la medición.
Por ejemplo, la persona que mide la longitud de un palo con una regla nota que la longitud del palo parece estar en algún lugar entre $36.6 \;cm$ y $36.7 \;cm$, y él o ella debe estimar el valor del último dígito.
Usando el método de cifras significativas, la regla es que el último dígito anotado en una medición es el primer dígito con cierta incertidumbre. Para determinar el número de dígitos significativos en un valor, comience con el primer valor medido a la izquierda y cuente el número de dígitos hasta el último dígito escrito a la derecha. Por ejemplo, el valor medido $36.7 \;cm$ tiene tres dígitos o tres cifras significativas. Las cifras significativas indican la precisión de la herramienta de medición utilizada para medir un valor.
Ceros
Se presta especial consideración a los ceros cuando se cuentan cifras significativas. Los ceros en $0.053$ no son significativos porque son marcadores de posición que ubican el punto decimal. Hay dos cifras significativas en $0.053$. Los ceros en $10.053$ no son marcadores de posición; ellos son significativos, Este número tiene cinco cifras significativas. Los ceros en $1300$ pueden o no ser significativos, dependiendo del estilo de escritura de los números. Podrían significar que el número es conocido por el último dígito o podrían ser marcadores de posición. Entonces, $1300$ podría tener dos, tres o cuatro cifras significativas.
Para evitar esta ambigüedad, deberíamos escribir $1300$ en notación científica como $1.3 \times 10^3, 1.30 \times 10^3$, o $1.300 \times 10^3$, dependiendo si tiene dos, tres o cuatro cifras. Los ceros son significativos, excepto cuando solo sirven como marcadores de posición.
Cifras significativas en los cálculos
Cuando se combinan mediciones con diferentes grados de precisión, el número de dígitos significativos en la respuesta final no puede ser mayor que el número de dígitos significativos en el valor medido menos preciso. Hay dos reglas diferentes, una para la multiplicación y la división y la otra para la suma y la resta.
- Para la multiplicación y la división, el resultado debe tener el mismo número de cifras significativas que la cantidad con el menor número de cifras significativas que entran en el cálculo. Por ejemplo, el área de un círculo se puede calcular a partir de su radio utilizando $A = \pi r^2$. Veamos cuántas figuras significativas tiene el área si el radio tiene solo dos, digamos, $r = 1.2 \;m$. Usando una calculadora con una salida de ocho dígitos, calcularíamos
$$A = \pi r^2 = (3.1415927…)\times (1.2 \;m)^2 = 4.5238934\; m^2$$ Pero como el radio tiene solo dos cifras significativas, limita la cantidad calculada a dos cifras significativas, o a $A = 4.5 \; m^2$, aunque $\pi$ es bueno para al menos ocho dígitos. - Para sumar y restar, la respuesta no puede contener más decimales que la medición menos precisa. Supongamos que compramos $7,56\; kg$ de papas en una tienda de abarrotes según lo medido con una báscula con precisión de $0,01\; kg$, luego dejamos caer $6,052 \;kg$ de papas en el laboratorio, según lo determinado por una balanza con una precisión de $0,001 kg$.
- Luego, nos vamos a casa y agregamos $13,7 \;kg$ de papas, según lo medido por una báscula de baño con una precisión de $0,1 \;kg$. ¿Cuántos kilogramos de patatas tenemos ahora y cuántas cifras significativas son apropiadas en la respuesta? La masa se encuentra por simple suma y resta: $7.56 \;kg - 6.052 \;kg + 13.7\; kg = 15.208\; kg$. A continuación, identificamos la medida menos precisa: $13,7\; kg$. Esta medida se expresa con el decimal de $0,1$, por lo que nuestra respuesta final también debe expresarse con el decimal de $0,1$. Por lo tanto, la respuesta se redondea al décimo lugar, lo que nos da $15,2\; kg$.
Cifras significativas en este texto
En este texto, se supone que la mayoría de los números tienen tres cifras significativas. Además, se usan números consistentes de cifras significativas en todos los ejemplos trabajados. Una respuesta dada a tres dígitos se basa en una entrada buena por lo menos a tres dígitos, por ejemplo, si la entrada tiene menos cifras significativas, la respuesta también tendrá menos cifras significativas. También se tiene cuidado de que el número de cifras significativas sea razonable para la situación planteada. En algunos temas, particularmente en óptica, se necesitan números más precisos y utilizamos más de tres cifras significativas. Finalmente, si un número es exacto, como los dos en la fórmula para la circunferencia de un círculo, $C = 2\pi r$, no afecta el número de cifras significativas en un cálculo.
Del mismo modo, los factores de conversión como $100\; cm/1\; m$ se consideran exactos y no afectan el número de cifras significativas en un cálculo.
Practica con la escena interactiva de la siguiente página, diseñada por Carlos Palacio GómezLa escena hace parte de una unidad de Física del Proyecto EDAD, publicado por le Red Descartes.. Observa las cifras del número y la imprecisión con que se conoce. Observa las cifras del número y la imprecisión con que se conoce.
Piensa cuál debe ser la cifra más significativa y la menos significativa antes de pulsar RESPUESTA para comprobarlo. Para averiguar el número de cifras significativas, sólo tendrás que contar el número de cifras que hay entre la más significativa y la menos significativa, ambas incluidas.
Resolviendo Problemas en Física
Las habilidades para la resolución de problemas son claramente esenciales para el éxito en un curso cuantitativo de física. Lo que es más importante, la capacidad de aplicar principios físicos amplios -generalmente representados por ecuaciones- a situaciones específicas, es una forma muy poderosa de conocimiento.
Es mucho más poderoso que memorizar una lista de hechos. Las habilidades analíticas y las habilidades para resolver problemas se pueden aplicar a situaciones nuevas, mientras que una lista de hechos no se puede hacer lo suficiente como para contener todas las circunstancias posibles.
Dichas habilidades analíticas son útiles tanto para resolver problemas en este texto, como para aplicar la física en la vida cotidiana. Como probablemente ya sepas, se requiere de cierta cantidad de creatividad y conocimiento para resolver problemas. Ningún procedimiento rígido funciona todo el tiempo. La creatividad y la visión crecen con la experiencia.

Con la práctica, los conceptos básicos para la resolución de problemas se vuelven casi automáticos. Una forma de obtener práctica es resolver los ejemplos del texto mientras lees. Otra, es resolver tantos problemas, al final de la sección, como sea posible, comenzando con los más fáciles para generar confianza y, luego, avanzando hacia los más complejos. Después de involucrarte en la Física, verás a tu alrededor y podrás comenzar a aplicarla a situaciones que encuentres fuera del aula, tal como se hace en muchas de las aplicaciones de este texto.
Aunque no existe un simple método paso a paso, que funcione para cada problema, el siguiente proceso de tres etapas facilita la resolución de problemas y lo hace más significativo. Las tres etapas son estrategia, solución y verificación. Este proceso se usa en ejemplos a lo largo del libro.
Estrategia
La estrategia es la etapa inicial para resolver un problema. La idea es descubrir exactamente cuál es el problema y luego desarrollar una estrategia para resolverlo. Algunos consejos generales para esta etapa son los siguientes:
- Examina la situación para determinar qué principios físicos están involucrados. A menudo, es útil dibujar un boceto simple al principio. Necesitas decidir qué dirección es positiva y anotar eso en tu boceto. Cuando hayas identificado los principios físicos, es mucho más fácil encontrar y aplicar las ecuaciones que representan esos principios. Aunque encontrar la ecuación correcta es esencial, ten en cuenta que las ecuaciones representan principios físicos, leyes de la naturaleza y relaciones entre cantidades físicas. Sin una comprensión conceptual de un problema, una solución numérica no tiene sentido.
- Haz una lista de lo que se da o se puede deducir del problema tal como se establece (identifica los "datos dados").
Muchos problemas se expresan de manera muy sucinta y requieren una cierta inspección para determinar lo que se conoce. Dibujar un boceto puede ser muy útil en este punto también. Formalmente, identificar los conocimientos es de particular importancia en la aplicación de la física a situaciones del mundo real. Por ejemplo, la palabra "parar" significa que la velocidad es cero en ese instante. Además, a menudo podemos tomar el tiempo inicial y la posición como cero mediante la elección adecuada del sistema de coordenadas. - Identifica exactamente qué debe determinarse en el problema (identifica las incógnitas). En problemas complejos, especialmente, no siempre es obvio lo que se necesita encontrar o en qué secuencia. Hacer una lista puede ayudar a identificar las incógnitas.
- Determina qué principios físicos pueden ayudarte a resolver el problema. Dado que los principios físicos tienden a expresarse en forma de ecuaciones matemáticas, una lista de datos e incógnitas puede ayudar aquí. Es más fácil si puedes encontrar ecuaciones que contienen solo un dato desconocido, es decir, todas las demás variables son conocidas, de modo que puedes resolver fácilmente lo desconocido. Si la ecuación contiene más de una variable desconocida, entonces se necesitan ecuaciones adicionales para resolver el problema. En algunos problemas, se deben determinar varias incógnitas para llegar a la que más se necesita. En tales problemas, es especialmente importante tener en cuenta los principios físicos para evitar perder el rumbo en un mar de ecuaciones. Puede que tengas que usar dos (o más) ecuaciones diferentes para obtener la respuesta final.
Solución
La etapa de solución es cuando haces los cálculos. Sustituye los datos (junto con sus unidades) en la ecuación apropiada y obten soluciones numéricas completas con unidades.
Es decir, haz el álgebra, el cálculo, la geometría o la aritmética necesarios para encontrar los datos desconocidos a partir de los conocidos, asegurándote de llevar las unidades a través de los cálculos. Este paso es claramente importante porque produce la respuesta numérica, junto con sus unidades. Sin embargo, ten en cuenta que esta etapa es solo un tercio del proceso general de resolución de problemas.
Verificación
Después de haber hecho los cálculos en la etapa de solución de la resolución de problemas, es tentador pensar que ya terminaste. Pero recuerda siempre que la física no es matemática. Más bien, al hacer física, utilizamos las matemáticas como una herramienta para ayudarnos a comprender la naturaleza. Entonces, después de obtener una respuesta numérica, siempre debes evaluar su significado:
- Verifica tus unidades. Si las unidades de la respuesta son incorrectas, se ha producido un error y debes volver sobre tus pasos anteriores para encontrarlo. Una forma de encontrar el error es verificar todas las ecuaciones que obtuviste para la consistencia dimensional. Sin embargo, ten en cuenta que las unidades correctas no garantizan que la parte numérica de la respuesta también sea correcta.
- Verifica la respuesta para ver si es razonable. ¿Tiene sentido? Este paso es extremadamente importante: el objetivo de la física es describir la naturaleza con precisión.
Para determinar si la respuesta es razonable, verifica tanto su magnitud como su signo, además de sus unidades. La magnitud debe ser consistente con una estimación aproximada de lo que debería ser. También debes comparar, razonablemente, con magnitudes de otras cantidades del mismo tipo. El letrero generalmente te informa sobre la dirección y debe ser consistente con tus expectativas previas. Tu juicio mejorará a medida que resuelvas más problemas de física, y te será posible hacer juicios más precisos con respecto a si la naturaleza describe adecuadamente la respuesta a un problema. Este paso devuelve el problema a su significado conceptual. Si puedes juzgar si la respuesta es razonable, tienes una comprensión más profunda de la física que ser capaz de resolver un problema mecánicamente.
- Verifica si la respuesta te dice algo interesante. ¿Qué significa eso? Esta es la otra cara de la pregunta: ¿Tiene sentido? En definitiva, la física trata de comprender la naturaleza y resolvemos los problemas de física para aprender algo sobre cómo funciona la naturaleza. Por lo tanto, suponiendo que la respuesta tiene sentido, siempre debes tomarte un momento para ver si te dice algo sobre el mundo que te parece interesante. Incluso si la respuesta a este problema en particular no es muy interesante para ti, ¿qué pasa con el método que utilizaste para resolverlo? ¿Podría el método adaptarse para responder a una pregunta que te parezca interesante? En muchos sentidos, es al responder preguntas como éstas que la ciencia progresa.
Vectores
Video publicado en TikTok, en el canal @claseconmaca
Introducción

Los vectores son esenciales para la física y la ingeniería. Muchas cantidades físicas fundamentales son vectores, incluidos el desplazamiento, la velocidad, la fuerza y los campos eléctricos y magnéticos. Los productos escalares de vectores definen otras cantidades físicas escalares fundamentales, como la energía. Los productos vectoriales de vectores definen todavía otras cantidades físicas de vectores fundamentales, como el par motor y el momento angular. En otras palabras, los vectores son una parte de la física de forma muy parecida a como las oraciones son una parte de la literatura.
En la física introductoria, los vectores son cantidades euclidianas que tienen representaciones geométricas como flechas en una dimensión (en una línea), en dos dimensiones (en un plano) o en tres dimensiones (en el espacio). Se pueden sumar, restar o multiplicar. En este capítulo, exploraremos elementos del álgebra vectorial para aplicaciones en mecánica y en electricidad y magnetismo. Las operaciones de vectores también tienen numerosas generalizaciones en otras ramas de la física.
Escalares y Vectores
Muchas cantidades físicas familiares pueden especificarse completamente dando un número único y la unidad apropiada. Por ejemplo, "un período de clase dura $50\; min$" o "el tanque de gasolina de mi automóvil tiene $65 \;L$" o "la distancia entre dos postes es de $100 \;m$". Una cantidad física que se puede especificar completamente de esta manera se denomina cantidad escalar. Escalar es un sinónimo de "número". El tiempo, la masa, la distancia, la longitud, el volumen, la temperatura y la energía son ejemplos de cantidades escalares.
Las cantidades escalares que tienen las mismas unidades físicas se pueden sumar o restar de acuerdo con las reglas habituales del álgebra para los números. Por ejemplo, una clase que termina $10$ minutos antes que $50 \;min$ dura $50\;min-10\;min = 40\;min$. De manera similar, una porción de maíz de $60$ calorías seguida de una porción de donas de $200$ calorías da $60\;cal + 200\;cal = 260\;cal$ de energía. Cuando multiplicamos una cantidad escalar por un número, obtenemos la misma cantidad escalar pero con un valor más grande (o más pequeño). Sin embargo, muchas cantidades físicas no se pueden describir completamente con solo un número de unidades físicas.
Por ejemplo, cuando la Guardia Costera de los EE. UU. despacha un barco o un helicóptero para una misión de rescate, el equipo de rescate debe conocer no solo la distancia a la señal de socorro, sino también la dirección desde la cual llega la señal para poder llegar a su origen lo más rápido posible.
Las cantidades físicas especificadas completamente dando un número de unidades (magnitud) y una dirección se llaman cantidades vectoriales. Ejemplos de cantidades de vectores incluyen desplazamiento, velocidad, posición, fuerza y torque. En el lenguaje de las matemáticas, las cantidades de vectores físicos están representadas por objetos matemáticos llamados vectores (Figura 2.2). Podemos sumar o restar dos vectores, y podemos multiplicar un vector por un escalar o por otro vector, pero no podemos dividir por un vector. La operación de división por un vector no está definida.
Por ejemplo, si el desayuno de ayer tenía $200$ calorías de energía y el desayuno de hoy tiene cuatro veces más energía que ayer, el desayuno de hoy tiene $4(200\;cal) = 800\;cal$ de energía. Dos cantidades escalares también se pueden multiplicar o dividir entre sí para formar una cantidad escalar derivada. Por ejemplo, si un tren cubre una distancia de $100 \;km$ en $1.0 \;h$, su velocidad es de $(100.0 \;km)/(1.0\; h) = 27.8\; m/s$, donde la velocidad es una cantidad escalar derivada obtenida al dividir la distancia por tiempo.
Sin embargo, muchas cantidades físicas no se pueden describir completamente con solo un número de unidades físicas. Por ejemplo, cuando la Guardia Costera de los EE. UU. Despacha un barco o un helicóptero para una misión de rescate, el equipo de rescate debe conocer no solo la distancia a la señal de socorro, sino también la dirección desde la cual llega la señal para poder llegar a su origen lo más rápido posible.
Las cantidades físicas especificadas completamente dando un número de unidades (magnitud) y una dirección se llaman cantidades vectoriales. Ejemplos de cantidades de vectores incluyen desplazamiento, velocidad, posición, fuerza y torque. En el lenguaje de las matemáticas, las cantidades de vectores físicos están representadas por objetos matemáticos llamados vectores (Figura 2.2). Podemos sumar o restar dos vectores, y podemos multiplicar un vector por un escalar o por otro vector, pero no podemos dividir por un vector. La operación de división por un vector no está definida.
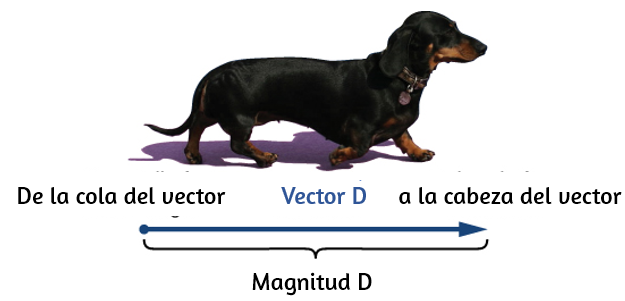
Examinemos el álgebra vectorial usando un método gráfico para conocer los términos básicos y desarrollar una comprensión cualitativa. En la práctica, sin embargo, cuando se trata de resolver problemas de física, utilizamos métodos analíticos, que veremos en la siguiente sección. Los métodos analíticos son más simples computacionalmente y más precisos que los métodos gráficos.
A partir de ahora, para distinguir entre un vector y una cantidad escalar, adoptamos la convención común de una letra en negrita con una flecha encima que denota a un vector, y una letra sin una flecha que denota a un escalar. Por ejemplo, una distancia de $2.0 km$, que es una cantidad escalar, se denota por $d = 2.0 km$, mientras que un desplazamiento de $2.0 km$ en alguna dirección, que es una cantidad vectorial, se denota por $\bold{\vec{d}}$.
Supongamos que le dices a un amigo en un viaje de campamento que has descubierto un fabuloso agujero para pescar a $6 km$ de tu tienda.
Es poco probable que tu amigo pueda encontrar el hoyo fácilmente a menos que también comuniques la dirección en la que se puede encontrar con respecto a tu campamento. Puedes decir, por ejemplo, "Camina unos $6 km$ al noreste de mi tienda". El concepto clave aquí es que debe dar no una sino dos datos de información, a saber, la distancia o magnitud ($6 km$) y la dirección (Noreste).
El desplazamiento es un término general usado para describir un cambio de posición, como durante un viaje desde la tienda de campaña hasta el agujero de pesca. El desplazamiento es un ejemplo de una cantidad vectorial. Si caminas desde la tienda (ubicación A) hasta el agujero (ubicación B), como se muestra en la Figura 2.3, el vector $\bold{\vec{D}}$, que representa tu desplazamiento, se dibuja como la flecha que se origina en el punto $A$ y termina en el punto $B$. La punta de flecha marca el final del vector. La dirección del vector de desplazamiento $\bold{\vec{D}}$ es la dirección de la flecha. La longitud de la flecha representa la magnitud $D$ del vector $\bold{\vec{D}}$ Aquí, $D = 6 km$. Como la magnitud de un vector es su longitud, que es un número positivo, la magnitud también se indica colocando la notación del valor absoluto alrededor del símbolo que denota el vector; entonces, podemos escribir equivalentemente que $D = |\bold{\vec{D}}|$.
Para resolver un problema vectorial gráficamente, necesitamos dibujar el vector $\bold{\vec{D}}$ a escala. Por ejemplo, si asumimos que 1 unidad de distancia ($1 km$) está representada en el dibujo por un segmento de línea de longitud $u = 2 cm$, entonces el desplazamiento total en este ejemplo está representado por un vector de longitud $d = 6u = 6(2 cm) = 12 cm$, como se muestra en la Figura 2.4.
Observa que aquí, para evitar confusiones, utilizamos $D = 6km$ para denotar la magnitud del desplazamiento real y $d = 12 cm$ para indicar la longitud de su representación en el dibujo.
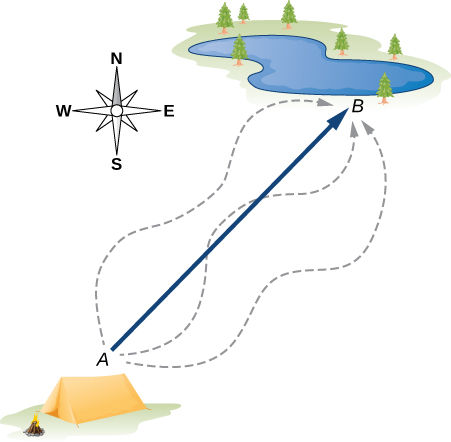
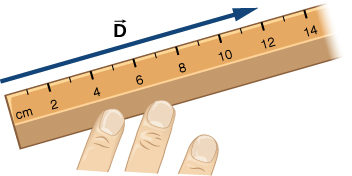
Supongamos que su amigo camina del campamento en $A$ al estanque de pesca en $B$ y luego regresa del estanque de pesca en $B$ al campamento en $A$. La magnitud del vector de desplazamiento $\bold{\vec{D}}_{AB}$ de $A$ a $B$ es la misma que la magnitud del vector de desplazamiento $\bold{\vec{D}}_{BA}$ de $B$ a $A$ (equivale a $6 km$ en ambos casos), por lo que podemos escribir $\bold{\vec{D}}_{AB} = \bold{\vec{D}}_{BA}$. Sin embargo, el vector $\bold{\vec{D}}_{AB}$ no es igual al vector $\bold{\vec{D}}_{BA}$ porque estos dos vectores tienen diferentes direcciones: $\bold{\vec{D}}_{AB} \ne \bold{\vec{D}}_{BA}$. En la Figura 2.3, el vector $\bold{\vec{D}}_{AB}$ estaría representado por un vector con un origen en el punto $B$ y un extremo en el punto $A$, indicando el vector $\bold{\vec{D}}_{BA}$ apunta al suroeste, que es exactamente $180\degree$ opuesto a la dirección del vector $\bold{\vec{D}}_{AB}$. Decimos que el vector $\bold{\vec{D}}_{BA}$ es antiparalelo al vector $\bold{\vec{D}}_{AB}$ y escribes $\bold{\vec{D}}_{BA} = -\bold{\vec{D}}_{AB}$, donde el signo menos indica la dirección antiparalela.
Se dice que dos vectores que tienen direcciones idénticas son vectores paralelos, lo que significa que son paralelos entre sí.
Dos vectores paralelos $\bold{\vec{A}}$ y $\bold{\vec{B}}$ son iguales, indicados por $\bold{\vec{A}} = \vec{\bold{B}}$, si y solo si tienen las mismas magnitudes $|\vec{\bold{A}}| = |\vec{\bold{B}}|$. Se dice que dos vectores con direcciones perpendiculares entre sí son vectores ortogonales. Estas relaciones entre vectores se ilustran en la Figura 2.5.
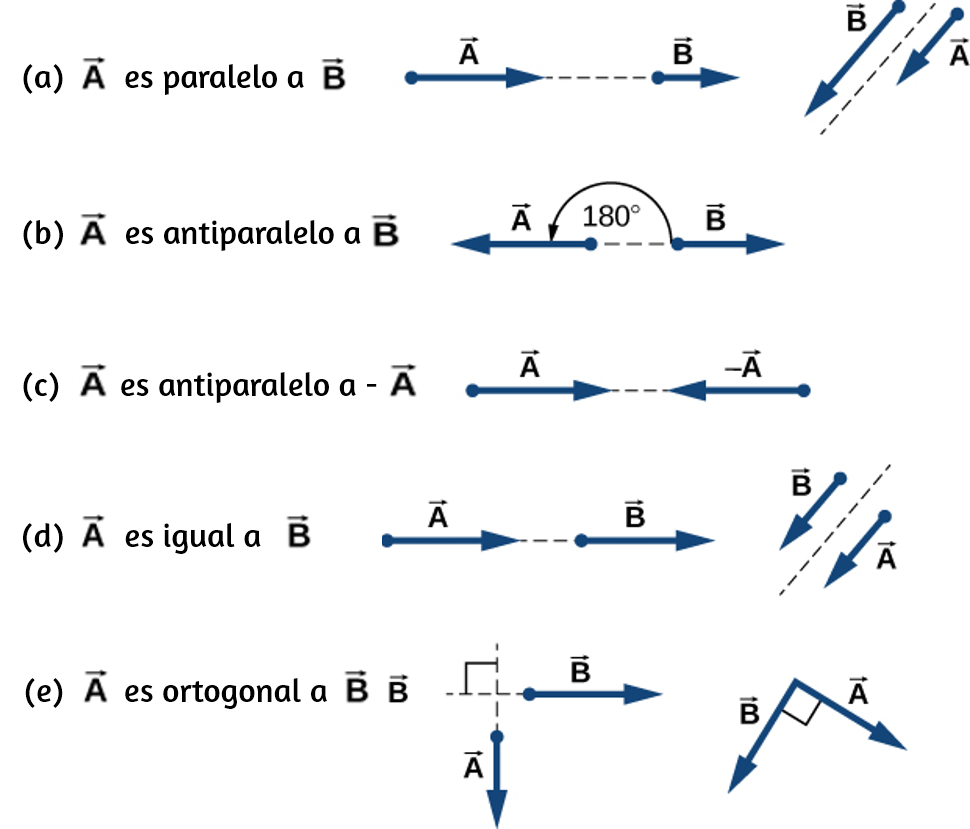
 Comprueba tu aprendizaje 2.1
Comprueba tu aprendizaje 2.1
Álgebra de vectores en una dimensión
Los vectores pueden multiplicarse por escalares, sumarse a otros vectores o restarse de otros vectores. Podemos ilustrar estos conceptos vectoriales usando un ejemplo del viaje de pesca que se ve en la Figura 2.6.
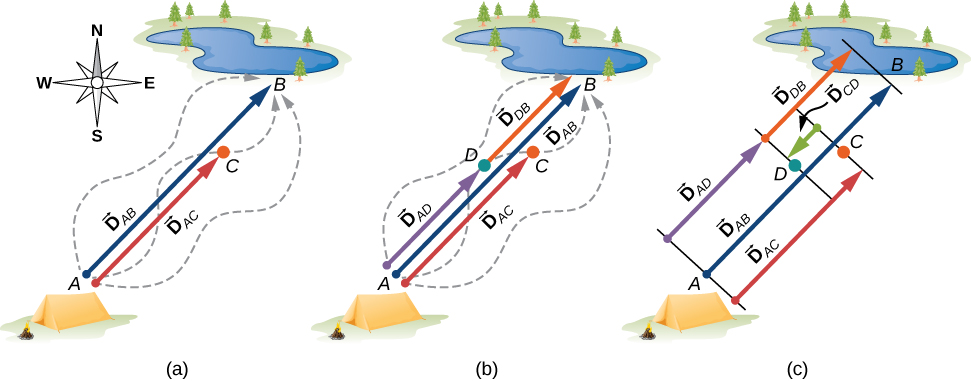
Supongamos que su amigo sale del punto $A$ (el campamento) y camina en dirección al punto $B$ (el estanque de pesca), pero, en el camino, se detiene para descansar en algún punto $C$ ubicado a tres cuartas partes de la distancia entre $A$ y $B$, comenzando desde el punto $A$ (Figura 2.6 (a)). ¿Cuál es su vector de desplazamiento$\bold{\vec{D}}_{AC}$ cuando alcanza el punto $C$? Sabemos que si camina todo el camino hasta $B$, su vector de desplazamiento relativo a $A$ es $\bold{\vec{D}}_{AB}$, que tiene una magnitud $D_{AB} = 6 \;km$ y una dirección de noreste. Si camina solo una fracción de $0.75$ de la distancia total, manteniendo la dirección noreste, en el punto $C$ debe ser $0.75 D_{AB} = 4.5 \;km$ lejos del campamento en $A$. Entonces, su vector de desplazamiento en el punto de descanso $C$ tiene una magnitud $D_{AC} = 4.5\; km = 0.75D_{AB}$ y es paralela al vector de desplazamiento $\bold{\vec{D}}_{AB}$ . Todo esto se puede establecer de manera sucinta en la forma de la siguiente ecuación vectorial:
$$\bold{\vec{D}}_{AC} = 0.75\bold{\vec{D}}_{AB}$$En una ecuación vectorial, ambos lados de la ecuación son vectores. La ecuación anterior es un ejemplo de un vector multiplicado por un escalar positivo (número) $\alpha = 0.75$. El resultado, $\bold{\vec{D}}D_{AC}$, de dicha multiplicación es un nuevo vector con una dirección paralela a la dirección del vector original $\bold{\vec{D}}_{AC}$.
En general, cuando un vector $\bold{\vec{A}}$ se multiplica por un escalar positivo $\alpha$, el resultado es un nuevo vector $\bold{\vec{B}}$ que es paralelo a $\bold{\vec{A}}$
$$ \bold{\vec{B}} = \alpha\bold{\vec{A}} \tag{2.1}$$
La magnitud $|\bold{\vec{B}}|$ de este nuevo vector se obtiene multiplicando la magnitud $|\bold{\vec{A}}|$ del vector original, según lo expresado por la ecuación escalar:
La siguiente escena interactiva representa la muliplicación del vector por un escalar. Cambia el valor de $\alpha$.
En una ecuación escalar, ambos lados de la ecuación son números. La ecuación 2.2 es una ecuación escalar porque las magnitudes de los vectores son cantidades escalares (y números positivos).
Si el escalar $\alpha$ es negativo en la ecuación 2.1, entonces la magnitud $|\bold{\vec{B}}|$ del nuevo vector todavía está dado por la ecuación 2.2, pero la dirección del nuevo vector $\bold{\vec{B}}$ es antiparalelo a la dirección de $\bold{\vec{A}}$. Estos principios se ilustran en la Figura 2.7 (a) mediante dos ejemplos en los que la longitud del vector $\bold{\vec{A}}$ es de $1,5$ unidades. Cuando $\alpha = 2$, el nuevo vector $\bold{\vec{B}} = 2\bold{\vec{A}}$ tiene longitud $B = 2A = 3.0 \text{ unidades}$ (dos veces más largas que el vector original) y es paralela al vector original. Cuando $\alpha = -2$, el nuevo vector $\bold{\vec{C}} = -2\bold{\vec{A}}$ y tiene longitud $C = |-2|A = 3.0 \text{ unidades}$ (el doble de longitud que el original vector) y es antiparalelo al vector original.
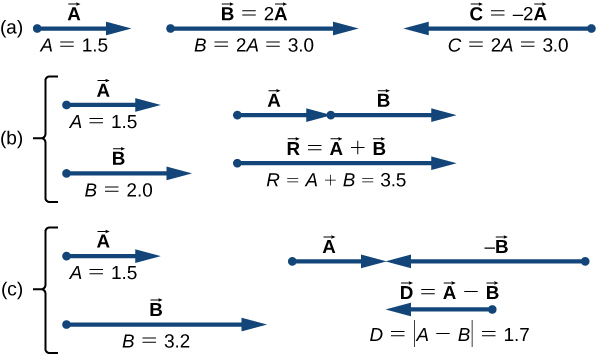
Ahora supongamos que su compañero de pesca sale del punto $A$ (el campamento), caminando en dirección al punto $B$ (el agujero), pero se da cuenta que perdió su caja de aparejos cuando se detuvo para descansar en el punto $C$ (ubicado a tres cuartos de distancia entre $A$ y $B$, comenzando desde $A$). Entonces, se da vuelta y retrocede sus pasos en dirección al campamento y encuentra la caja en el camino en algún punto $D$ a solo $1.2 km$ del punto $C$ (ver Figura 2.6 (b)). ¿Cuál es su vector de desplazamiento $\bold{\vec{D}}_{AD}$ cuando encuentra la caja en el punto $D$?
¿Cuál es el vector de desplazamiento $\bold{\vec{D}}_{DB}$ del punto $D$ al agujero? Ya hemos establecido que en el punto de reposo $C$ el vector de desplazamiento es $\bold{\vec{D}}_{AC} = 0.75\bold{\vec{D}}_{AB}$. Comenzando en el punto $C$, camina hacia el sudoeste (hacia el campamento), lo que significa que el nuevo vector de desplazamiento $\bold{\vec{D}}_{CD}$ desde el punto $C$ al punto $D$ es antiparalelo a $\bold{\vec{D}}_{AB}$. Su magnitud $\bold{\vec{D}}_{|CD|}$ es $\bold{\vec{D}}_{CD} = 1.2km = 0.2\bold{\vec{D}}_{AB}$, entonces el segundo vector es $\bold{\vec{D}}_{CD} = -0.2\bold{\vec{D}}_{AB}$. El desplazamiento total $\bold{\vec{D}}_{AD}$ relativo al campamento es la suma vectorial de los dos vectores de desplazamiento: $\bold{\vec{D}}_{AC}$ (desde el camping hasta el punto de descanso) y $\bold{\vec{D}}_{CD}$ (desde el punto de descanso hasta el punto donde él encuentra su caja).
La suma de dos (o más) vectores se llama vector resultante o, para abreviar, la resultante. Cuando se conocen los vectores en el lado derecho de la ecuación 2.3, podemos encontrar la resultante $\bold{\vec{D}}_{AD}$ de la siguiente manera:
Cuando su amigo finalmente llega al estanque en $B$, su vector de desplazamiento $\bold{\vec{D}}_{AB}$ del punto $A$ es la suma vectorial del vector de desplazamiento$\bold{\vec{D}}_{AD}$ del punto $A$ al punto $D$y el vector de desplazamiento $\bold{\vec{D}}_{DB}$ del punto $D$ al agujero de pesca: $\bold{\vec{D}}_{AB} = \bold{\vec{D}}_{AD} + \bold{\vec{D}}_{BD}$ (ver Figura 2.6 (c)). Esto significa que el vector de desplazamiento $\bold{\vec{D}}_{DB}$ es la diferencia de dos vectores:
$$D\bold{\vec{D}}_{DB} = \bold{\vec{D}}_{AB} - \bold{\vec{D}}_{AD} = \bold{\vec{D}}_{AB} + (-\bold{\vec{D}}_{AD})\tag{2.5}$$Observa que una diferencia de dos vectores no es más que una suma vectorial de dos vectores porque el segundo término en la Ecuación 2.5 es el vector $-\bold{\vec{D}}_{AD}$ (que es antiparalelo a $\bold{\vec{D}}_{AD}$). Cuando sustituimos la Ecuación 2.4 en la Ecuación 2.5, obtenemos el segundo vector de desplazamiento:
$$\begin{split} \bold{\vec{D}}_{DB} &= \bold{\vec{D}}_{AB} - \bold{\vec{D}}_{AD} = \bold{\vec{D}}_{AB} - 0.55\bold{\vec{D}}_{AB}\\ &= (1.00 - 0.55)\bold{\vec{D}}_{AB} = 0.45\bold{\vec{D}}_{AB}\tag{2.6} \end{split}$$Este resultado significa que su amigo caminó $D_{DB} = 0.45D_{AB} = 0.45(6.0 \;km) = 2.7 \;km$ desde el punto donde encuentra su caja de aparejos hasta el agujero de pesca.
Cuando los vectores $\bold{\vec{A}}$ y $\bold{\vec{B}}$ se encuentran a lo largo de una línea (es decir, en una dimensión), como en el ejemplo de acampada, su resultante $\bold{\vec{R}} = \bold{\vec{A}} + \bold{\vec{B}}$ y su diferencia $\bold{\vec{D}} = \bold{\vec{A}} - \bold{\vec{B}}$, se encuentran en la misma dirección.
Podemos ilustrar la suma o resta de vectores dibujando los vectores correspondientes para escalar en una dimensión, como se muestra en la Figura 2.7.
Para ilustrar la resultante cuando $\bold{\vec{A}}$ y $\bold{\vec{B}}$ son dos vectores paralelos, los dibujamos a lo largo de una línea colocando el origen de un vector en el extremo del otro vector de la cabeza a la cola (ver Figura 2.7 (b)). La magnitud de esta resultante es la suma de sus magnitudes: $R = A + B$. La dirección de la resultante es paralela a ambos vectores. Cuando el vector $\bold{\vec{A}}$ es antiparalelo al vector $\bold{\vec{B}}$, los dibujamos a lo largo de una línea en forma cabeza a cabeza (Figura 2.7 (c)) o de la cola a la cola. La magnitud de la diferencia vectorial, entonces, es el valor absoluto $D = | A-B | D = | A-B |$ de la diferencia de sus magnitudes. La dirección del vector de diferencia $\bold{\vec{D}}$ es paralela a la dirección del vector más largo.
En general, en una dimensión, así como en dimensiones superiores, como en un plano o en el espacio, podemos agregar cualquier número de vectores y podemos hacerlo en cualquier orden porque la adición de vectores es conmutativa,
y asociativa,
Además, la multiplicación por un escalar es distributiva:
Usamos la propiedad distributiva en la Ecuación 2.4 y la Ecuación 2.6.
Al agregar muchos vectores en una dimensión, es conveniente usar el concepto de un vector unitario. Un vector unitario, que se denota con un símbolo de letra con un sombrero, como $\^{\bold{u}}$, tiene una magnitud de uno y no tiene ninguna unidad física, por lo que $|\^{\bold{u}}| \equiv u = 1$. El único papel de un vector unitario es especificar la dirección. Por ejemplo, en lugar de decir que el vector $\bold{\vec{D}}_{AB}$ tiene una magnitud de $6.0 km$ y una dirección del noreste, podemos introducir un vector unitario $\bold{\^{u}}$ que apunta al noreste y decir sucintamente que $\bold{\vec{D}}_{AB} = (6.0 km)\bold{\^{u}}$. Entonces, la dirección del sudoeste simplemente está dada por el vector unitario $\bold{\^{u}}$. De esta forma, el desplazamiento de $6.0 km$en dirección suroeste se expresa mediante el vector
$$\bold{\vec{D}}_{BA} = (-6.0 km)\bold{\^{u}}$$Ejemplo 2.1
Una mariquita caminante
Una larga vara de medir descansa contra una pared en un laboratorio de física con su extremo de $200 cm$ en el piso. Una mariquita aterriza en la marca de $100 cm$ y se arrastra aleatoriamente a lo largo de la vara. Primero camina $15 cm$ hacia el piso, luego camina $56 cm$ hacia la pared, luego camina $3 cm$ hacia el piso nuevamente.
Luego, después de una breve parada, continúa durante $25 cm$ hacia el piso y luego, de nuevo, se arrastra $19 cm$ hacia la pared antes de descansar por completo (Figura 2.8). Encuentra el vector de su desplazamiento total y su posición de descanso final en la vara.
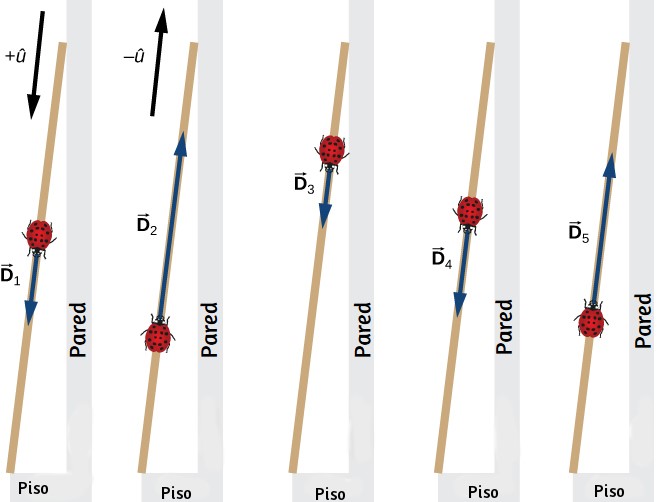
Estrategia
Si elegimos la dirección a lo largo del palo hacia el piso como la dirección del vector unitario $\bold{\^{u}}$, entonces la dirección hacia el piso es $+\bold{\^{u}}$ y la dirección hacia la pared es $-\bold{\^{u}}$. La mariquita hace un total de cinco desplazamientos:
El desplazamiento total $\bold{\vec{D}}$ es la resultante de todos los vectores de desplazamiento.
Solución
La resultante de todos los vectores de desplazamiento es
$$\begin{split} \bold{\vec{D}} &= \bold{\vec{D}}_1 + \bold{\vec{D}}_2 + \bold{\vec{D}}_3 + \bold{\vec{D}}_4 + \bold{\vec{D}}_5\\ &= (15cm)(+\bold{\^{u}}) + (56cm)(-\bold{\^{u}}) + (3cm)(+\bold{\^{u}}) \\ & \;\;\;\;+ (25cm)(+\bold{\^{u}} ) + (19cm)(-\bold{\^{u}})\\ &= (-32cm)\bold{\^{u}} \end{split}$$En este cálculo, usamos la ley distributiva dada por la Ecuación 2.9. El resultado dice que el vector de desplazamiento total se aleja de la marca de $100 cm$ (sitio de aterrizaje inicial) hacia el extremo de la vara que toca la pared.
El extremo que toca la pared está marcado en $0 cm$, por lo que la posición final de la mariquita está en la marca
$(100 - 32) cm = 68 cm$.
 Comprueba tu aprendizaje 2.2
Comprueba tu aprendizaje 2.2
Álgebra de vectores en dos dimensiones
Cuando los vectores se encuentran en un plano, es decir, cuando están en dos dimensiones, pueden multiplicarse por escalares, sumarse a otros vectores o restarse de otros vectores de acuerdo con las leyes generales expresadas por la Ecuación 2.1, Ecuación 2.2, Ecuación 2.7 y ecuación 2.8. Sin embargo, la regla de adición para dos vectores en un plano se vuelve más complicada que la regla para la adición de vectores en una dimensión. Tenemos que usar las leyes de la geometría para construir los vectores resultantes, seguidos de la trigonometría para encontrar las magnitudes y direcciones del vector. Este enfoque geométrico se usa comúnmente en navegación (Figura 2.9). En esta sección, necesitamos tener a mano dos reglas, un triángulo, un transportador, un lápiz y un borrador para dibujar vectores a escala mediante construcciones geométricas.
Para una construcción geométrica de la suma de dos vectores en un plano, seguimos la regla del paralelogramo. Supongamos que dos vectores $ \bold{\vec{A}}$ y $\bold{\vec{B}}$ están en las posiciones arbitrarias que se muestran en la Figura 2.10.

Traslada cualquiera de ellos en paralelo al comienzo del otro vector, de modo que después de la traslación, ambos vectores tengan su origen en el mismo punto. Ahora, al final del vector $\bold{\vec{A}}$ dibujamos una línea paralela al vector $\bold{\vec{B}}$ y al final del vector $\bold{\vec{B}}$ dibujamos una línea paralela al vector $\bold{\vec{A}}$ (las líneas discontinuas en la Figura 2.10). De esta forma, obtenemos un paralelogramo. Del origen de los dos vectores dibujamos una diagonal que es la resultante $\bold{\vec{R}}$ de los dos vectores: $\bold{\vec{R}} = \bold{\vec{A}} + \bold{\vec{B}}$ (Figura 2.10 (a)).
La otra diagonal de este paralelogramo es la diferencia vectorial de los dos vectores $\bold{\vec{D}} = \bold{\vec{A}} - \bold{\vec{B}}$, como se muestra en la Figura 2.10 (b). Observa que el final del vector diferencia se coloca al final del vector $\bold{\vec{A}}$.
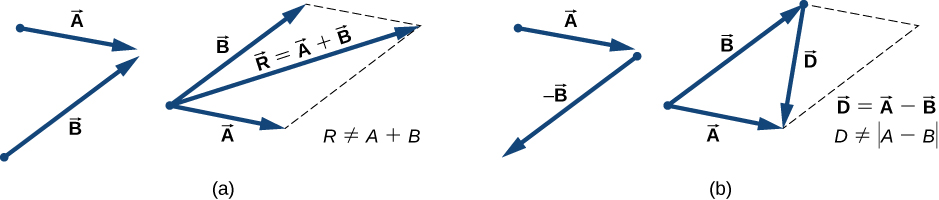
De la regla del paralelogramo se desprende que ni la magnitud del vector resultante ni la magnitud del vector diferencia se pueden expresar como una suma o diferencia simple de magnitudes A y B, porque la longitud de una diagonal no se puede expresar como una simple suma de longitudes laterales. Cuando se usa una construcción geométrica para encontrar magnitudes $|\bold{\vec{R}}|$ y $|\bold{\vec{D}}|$, tenemos que usar leyes de trigonometría para triángulos, lo que puede llevar al álgebra complicada. Hay dos formas de eludir esta complejidad algebraica. Una forma es usar el método de los componentes, que examinamos en la siguiente sección. La otra forma es dibujar los vectores a escala, como se hace en navegación, y leer longitudes aproximadas de los vectores y ángulos (direcciones) de los gráficos.
En esta sección examinamos el segundo enfoque. Pero antes de ello, observa los siguientes vídeos y escenas interactivas diseñadas con el editor DescartesJS.
Video
En los vídeos se muestran tres métodos para sumar vectores en el plano que, para este caso, corresponden a fuerzas aplicadas en un elemento mecánico. El primer método es el del paralelogramo, y los otros dos están asociados al método del polígono, que consiste en unir cabezas con colas para, posteriormente, conformar el polígono con el vector o fuerza resultante.
En la siguiente escena interactiva, diseñada por Juan Guillermo Rivera B., se explica, paso a paso, el método del paralelogramo. Puedes cambiar la dirección de los vectores, usando el botón pulsador. La escena fue diseñada para un curso de mecánica (estática), por ello, los vectores corresponden a fuerzas aplicadas en un punto.
¡Haz clic en el botón de la esquina superior derecha, para ampliar la escena!
Si necesitamos agregar tres o más vectores, repetimos la regla del paralelogramo para los pares de vectores hasta que encontremos la resultante de todos los resultados. Para tres vectores, por ejemplo, primero encontramos la resultante del vector 1 y el vector 2, y luego encontramos la resultante de este vector resultante 3.
El orden en el que seleccionamos los pares de vectores no importa porque las operaciones entre vectores es conmutativa y asociativa (ver Ecuación 2.7 y Ecuación 2.8). Antes de que establezcamos una regla general (como la observada en el tercer vídeo), que se deduce de las aplicaciones repetitivas de la regla del paralelogramo, veamos el siguiente ejemplo.
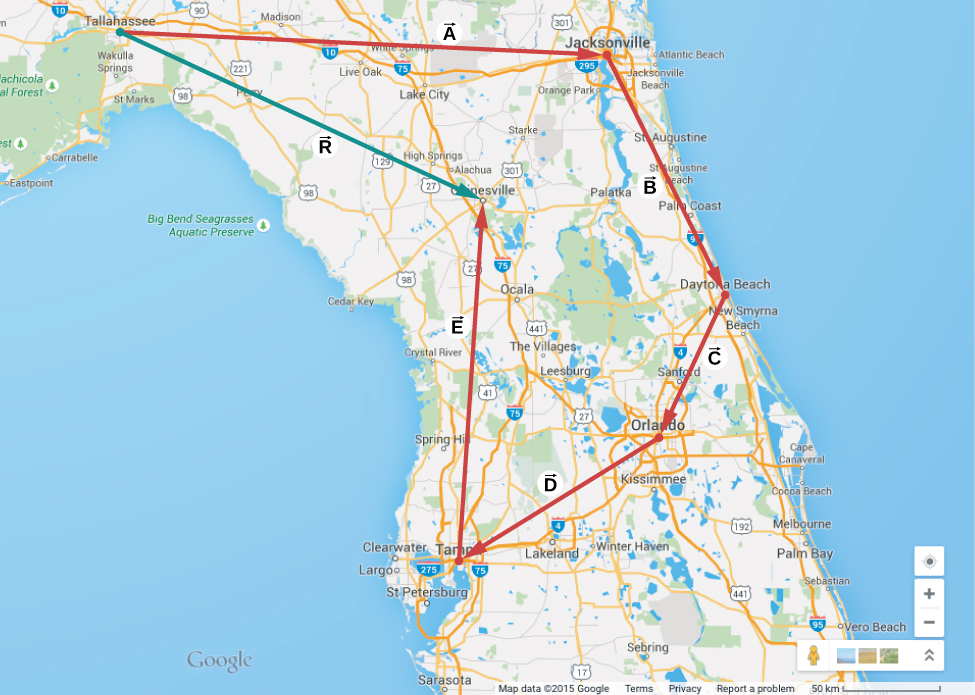
Supongamos que planificas un viaje de vacaciones en Florida. Saliendo de Tallahassee, la capital del estado, planeas visitar a tu tío Joe en Jacksonville, ver a tu primo Vinny en Daytona Beach, detenerte a divertirte un poco en Orlando, ver un espectáculo de circo en Tampa y visitar la Universidad de Florida en Gainesville. Tu ruta puede estar representada por cinco vectores de desplazamiento $\bold{\vec{A}}, \bold{\vec{B}}, \bold{\vec{C}}, \bold{\vec{D}} \text{ y } \bold{\vec{E}}$, que están indicados por los vectores rojos en la Figura 2.11. ¿Cuál es tu desplazamiento total cuando llegas a Gainesville? El desplazamiento total es la suma vectorial de los cinco vectores de desplazamiento, que se pueden encontrar al usar la regla del paralelogramo cuatro veces.
Alternativamente, recuerda que el vector de desplazamiento tiene su comienzo en la posición inicial (Tallahassee) y su final en la posición final (Gainesville), por lo que el vector de desplazamiento total se puede dibujar directamente como una flecha que conecta Tallahassee con Gainesville (observa el vector verde en la Figura 2.11). Cuando usamos la regla del paralelogramo cuatro veces, la resultante $\bold{\vec{R}}$ es exactamente este vector verde que conecta Tallahassee con Gainesville: $\bold{\vec{R}} = \bold{\vec{A}} + \bold{\vec{B}} + \bold{\vec{C}} + \bold{\vec{D}} + \bold{\vec{E}}$.
Dibujar el vector resultante de muchos vectores se puede generalizar usando la siguiente construcción geométrica de la cabeza a la cabeza. Supongamos que queremos dibujar el vector resultante $\bold{\vec{R}}$ de cuatro vectores $\bold{\vec{A}}, \bold{\vec{B}}, \bold{\vec{C}}\text{ y } \bold{\vec{D}}$ (Figura 2.12 (a)). Seleccionamos cualquiera de los vectores como primer vector y hacemos una traslación paralela de un segundo vector a una posición donde el origen ("cola") del segundo vector coincide con el final ("cabeza") del primer vector. Luego, seleccionamos un tercer vector y hacemos una traslación paralela del tercer vector a una posición donde el origen del tercer vector coincide con el final del segundo vector. Repetimos este procedimiento hasta que todos los vectores estén en una disposición de cabeza a cola como la que se muestra en la Figura 2.12 y en el tercer vídeo anterior. Dibujamos el vector resultante $\bold{\vec{R}}$ conectando el origen ("cola") del primer vector con el final ("cabeza") del último vector.
El final del vector resultante está al final del último vector. Debido a que la adición de vectores es asociativa y conmutativa, obtenemos el mismo vector resultante independientemente del vector que elijamos para ser el primero, el segundo, el tercero o el cuarto en esta construcción.
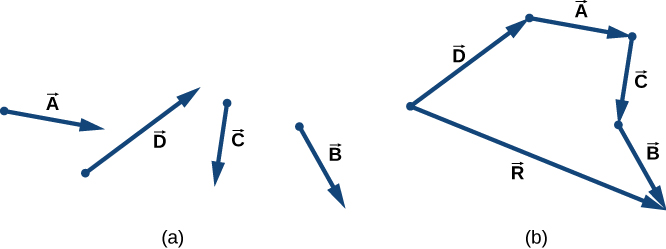
Ejemplo 2.2
Construcción geométrica de la resultante
Los tres vectores de desplazamiento $\bold{\vec{A}}, \bold{\vec{B}} \text{ y } \bold{\vec{C}}$ en la Figura 2.13 se especifican por sus magnitudes $A = 10.0, B = 7.0 \text{ y } C = 8.0$, respectivamente, y por sus respectivos ángulos de dirección con la dirección horizontal $\alpha = 35\degree, \beta = -110\degree$ y $\gamma = 30\degree$. Las unidades físicas de las magnitudes son centímetros.
Elige una escala conveniente y usa una regla y un transportador para encontrar las siguientes sumas de vectores: (a) $\bold{\vec{R}} = \bold{\vec{A}} + \bold{\vec{B}}$, (b) $ \bold{\vec{D}}= \bold{\vec{A}} - \bold{\vec{B}}$ y (c) $\bold{\vec{S}}= \bold{\vec{A}} - 3\bold{\vec{B}}+ \bold{\vec{C}}$
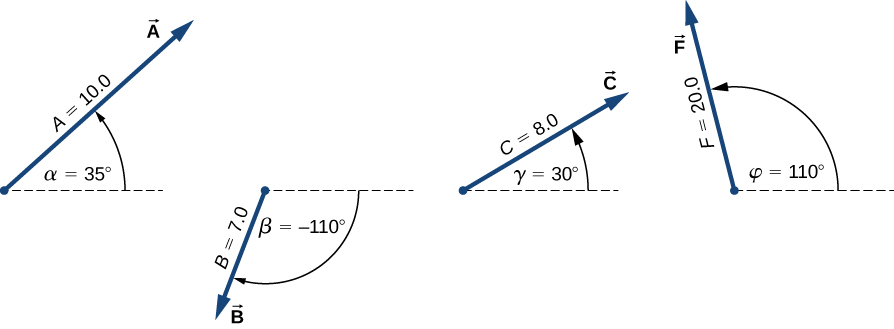
Estrategia
En la construcción geométrica, encontrar un vector significa encontrar su magnitud y su ángulo de dirección con la dirección horizontal. La estrategia es dibujar para escalar los vectores que aparecen en el lado derecho de la ecuación y construir el vector resultante. Luego, usar una regla y un transportador para leer la magnitud de la resultante y el ángulo de dirección. Para las partes (a) y (b) usamos la regla del paralelogramo. Para (c) usamos el método de cabeza y cola o del polígono.
Solución
Para las partes (a) y (b), adjuntamos el origen del vector $\bold{\vec{B}}$ al origen del vector $\bold{\vec{A}}$ como se muestra en la Figura 2.14, y construimos un paralelogramo. La diagonal más corta de este paralelogramo es la suma $\bold{\vec{A}} + \bold{\vec{B}}$. La más larga de las diagonales es la diferencia $\bold{\vec{A}} - \bold{\vec{B}}$. Usamos una regla para medir las longitudes de las diagonales, y un transportador para medir los ángulos con la horizontal. Para la resultante $\bold{\vec{R}}$, obtenemos $R = 5.8 cm$ y $\theta_R \approx 0\degree$.
Para la diferencia $\bold{\vec{D}}$, obtenemos $D = 16.2 cm$ y $\theta_D = 49.3\degree$, que se muestran en la Figura 2.14.
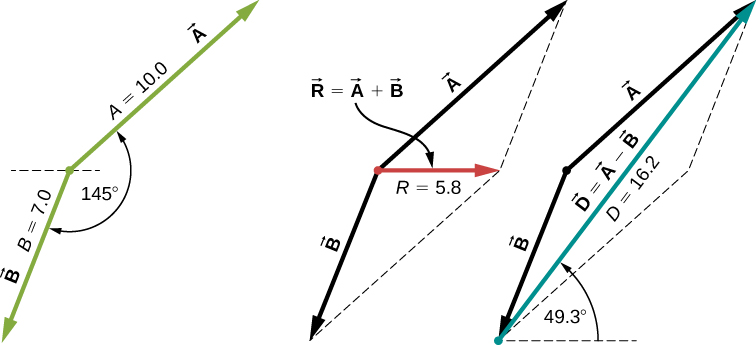
Para (c), podemos comenzar con el vector $-3\bold{\vec{B}} + \bold{\vec{B}}$ y dibujar los vectores restantes a la cola como se muestra en la Figura 2.15. En la suma de vectores, el orden en que los dibujamos no es importante, pero dibujar los vectores a escala es muy importante.
A continuación, dibujamos el vector $\bold{\vec{S}} + \bold{\vec{B}}$ desde el origen del primer vector hasta el final del último y colocamos la punta de flecha al final de $\bold{\vec{S}}+ \bold{\vec{B}}$. Usamos una regla para medir la longitud de $\bold{\vec{S}} + \bold{\vec{B}}$, y encontramos que su magnitud es $S = 36.9 cm$.
Usamos un transportador y descubrimos que su ángulo de dirección es $\theta_S = 52.9\degree$. Esta solución se muestra en la Figura 2.15.
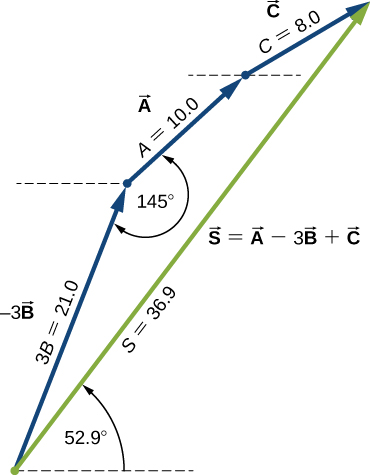
 Comprueba tu aprendizaje 2.3
Comprueba tu aprendizaje 2.3
Finalmente, practica el método de cabeza y cola en la siguiente escena interactiva diseñada por Juan Guillermo Rivera B.
Sistemas de coordenadas y componentes de un vector
Los vectores se describen, generalmente, en términos de sus componentes en un sistema de coordenadas. Incluso en la vida cotidiana, invocamos el concepto de proyecciones ortogonales en un sistema de coordenadas rectangulares. Por ejemplo, si le preguntas a alguien por direcciones de una ubicación particular, lo más probable es que te diga que vayas $40 km$ al este y $30 km$ al norte, y no $50 km$ en la dirección $37\degree$ nordeste.
En un sistema de coordenadas $xy$ rectangular (cartesiano) en un plano, un punto en un plano se describe mediante un par de coordenadas $(x, y)$.
De manera similar, un vector $\bold{\vec{A}}$ en un plano se describe mediante un par de coordenadas. La coordenada $x$ del vector $\bold{\vec{A}}$ se denomina componente $x$ y la coordenada $y$ del vector $\bold{\vec{A}}$ se denomina componente $y$. La componente $x$ del vector es denotada por $\bold{\vec{A}}_x$. La componente $y$ del vector es denotada por $\bold{\vec{A}}_y$. En el sistema cartesiano, las componentes $x$ e $y$ del vector son las proyecciones ortogonales de este vector en los ejes $x$ e $y$, respectivamente. De esta manera, siguiendo la regla de paralelogramo para la suma de vectores, cada vector en un plano cartesiano puede expresarse como la suma de vectores de sus componentes de vector:
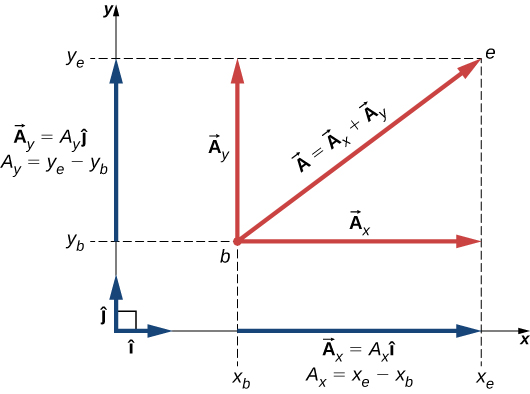
Como se ilustra en la Figura 2.16, el vector $\bold{\vec{A}}$ es la diagonal del rectángulo donde al componente $\bold{\vec{A}}_x$ es el lado paralelo al eje $x$, y la componente $\bold{\vec{A}}_y$ es el lado paralelo al eje $y$. La componente $\bold{\vec{A}}_x$ es ortogonal a la componente $\bold{\vec{A}}_y$.
Es costumbre denotar la dirección positiva en el eje $x$ por el vector unitario $\^{\bold{i}}$ y la dirección positiva en el eje $y$ por el vector unitario $\^{\bold{j}}$. Los vectores unitarios de los ejes, $\^{\bold{i}}$ y $\^{\bold{j}}$, definen dos direcciones ortogonales en el plano. Como se muestra en la Figura 2.16, las componentes rectangulares $x$ e $y$ de un vector ahora se pueden escribir en términos de los vectores unitarios de los ejes:
$$ \bold{\vec{A}}_x = Ax\^{\bold{i}}\\ \bold{\vec{A}}_y = A_y\^{\bold{j}}\tag{2.11}$$En la siguiente escena interactiva, diseñada por Juan Guillermo Rivera Berrío, desplaza el vector $\bold{\vec{A}}$ para que observar las componentes rectangulares del vector en cualquier dirección.
Los vectores $\bold{\vec{A}}_x$ y $\bold{\vec{A}}_y$ definidos por la ecuación 2.11 son las componentes rectangulares del vector $\bold{\vec{A}}$. Los números $A_x$ y $A_y$ que definen las componentes del vector en la Ecuación 2.11 son las componentes escalares del vector $\bold{\vec{A}}$. Combinando la Ecuación 2.10 con la Ecuación 2.11, obtenemos:
Si conocemos las coordenadas de los puntos $b\;(x_b, y_b)$ y las coordenadas del punto $e\; (x_e, y_e)$, podemos obtener las componentes escalares del vector (Observa la Figura 2.16), simplemente restando las coordenadas del punto de origen (b) de las coordenadas del punto final (e):
$$A_x = x_e - x_b\\ Ay = u_e - y_b\tag{2.13}$$
Ejemplo 2.3
Desplazamiento del puntero del ratón
Un puntero del ratón sobre el monitor de una computadora, en su posición inicial, está en el punto $(6.0 cm, 1.6 cm)$ con respecto a la esquina inferior izquierda. Si mueves el puntero a un icono ubicado en el punto $(2,0 cm, 4,5 cm)$, ¿cuál es el vector de desplazamiento del puntero?
Estrategia
El origen del sistema de coordenadas $xy$ es la esquina inferior izquierda del monitor de la computadora. Por lo tanto, el vector unitario $\^{\bold{i}}$ en el eje $x$ apunta horizontalmente hacia la derecha y el vector unitario $\^{\bold{j}}$ en el eje $y$ apunta verticalmente hacia arriba. El origen del vector de desplazamiento se encuentra en el punto $b \;(6.0, 1.6)$ y el extremo del vector de desplazamiento está ubicado en el punto $e \;(2.0, 4.5)$. Sustituye las coordenadas de estos puntos en la Ecuación 2.13 para encontrar los componentes escalares $D_x$ y $D_y$ del vector de desplazamiento $\bold{\vec{D}}$. Finalmente, sustituye las coordenadas en la ecuación 2.12 para escribir el vector de desplazamiento en la forma de las componentes rectangulares.
Solución
Identificamos $x_b = 6.0x, x_e = 2.0x, y_b = 1.6, y_e = 4.5$, donde la unidad física es $1 \;cm$. Los componentes escalares $x$ e $y$ del vector de desplazamiento son:
$$D_x = x_e − x_b = (2.0 − 6.0)cm = −4.0cm,\\ D_y = y_e − y_b = (4.5 − 1.6)cm = +2.9cm$$La forma vectorial del vector de desplazamiento es
$$\begin{split} \bold{\vec{D}} &= D_x\^{\bold{i}} + D_y\^{\bold{j}} \\ &= (−4.0cm)\^{\bold{i}} + (2.9cm)\^{\bold{j}}\\ &= (−4.0\^{\bold{i}} + 2.9\^{\bold{j}})cm\tag{2.14} \end{split}$$Esta solución se muestra en la Figura 2.17.
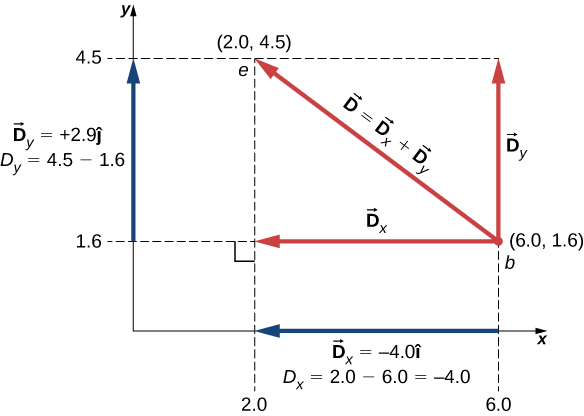
Verificación
Observa que la unidad física, aquí, $1 \;cm$, puede colocarse con cada componente inmediatamente antes del vector unitario o globalmente para ambos componentes, como en la Ecuación 2.14. A menudo, la última forma es más conveniente porque es más simple.
La componente rectangular $\bold{\vec{A}}_x = -4.0\^{\bold{i}} = 4.0\^{\bold{i}}$ del vector de desplazamiento tiene la magnitud $|\bold{\vec{A}_x}|= |-4.0 ||\^{\bold{i}}| = 4.0$ porque la magnitud del vector unitario es $|\^{\bold{i}}| = 1$.
Nótese también que la dirección de la componente en $x$ es $-\^{\bold{i}}î$, que es antiparalela a la dirección del eje $+x$; por lo tanto, la componente $\bold{\vec{D}}_x$ apunta hacia la izquierda, como se muestra en la figura 2.17. La componente escalar en $x$ del vector $\bold{\vec{D}}$ es $D_x = -4.0$.
De forma similar, la componente $\bold{\vec{D}}_y = +2.9\^{\bold{j}}$ del vector de desplazamiento tiene una magnitud $|\bold{\vec{D}}_y| = |2.9||\^{\bold{j}}| = 2.9$ porque la magnitud del vector unitario es $|\^{\bold{j}}| = 1$. La dirección del componente y es $+ \^{\bold{j}}$, que es paralela a la dirección del eje $+y$. Por lo tanto, la componente $\bold{\vec{D}}_y$ apunta hacia arriba, como se ve en la Figura 2.17. La componente y el escalar del vector $\bold{\vec{D}}$ es $D_y = + 2.9$.
Las componentes rectangulares del vector de desplazamiento nos dicen que el puntero del mouse ha sido movido en el monitor $4.0 cm$ hacia la izquierda y $2.9 cm$ hacia arriba desde su posición inicial.
 Comprueba tu aprendizaje 2.4
Comprueba tu aprendizaje 2.4
Cuando conocemos los componentes escalares $A_x$ y $A_y$ de un vector $\bold{\vec{A}}$, podemos encontrar su magnitud $A$ y su ángulo de dirección $\theta_A$.
El ángulo de dirección o dirección, para abreviar, es el ángulo que el vector forma con la dirección positiva en el eje $x$. El ángulo $\theta_A$ se mide en sentido antihorario desde el eje $+x$ al vector (Figura 2.18). Debido a que las longitudes $A, A_x$ y $A_y$ forman un triángulo rectángulo, están relacionadas por el teorema de Pitágoras:
$$A^2 = A_x^2 + A_y^2 \iff A = \sqrt{A_x^2 + A_y^2}$$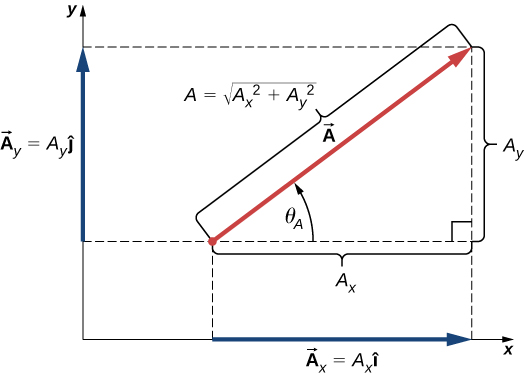
La ecuación funciona incluso si los componentes escalares de un vector son negativos. El ángulo de dirección $\theta_A$ de un vector se define mediante la función tangente del ángulo $\theta_A$ en el triángulo que se muestra en la Figura 2.18:
Cuando el vector yace en el primer cuadrante o en el cuarto cuadrante, donde el componente $A_x$ es positivo (Figura 2.19), el ángulo $\theta$ en la Ecuación 2.16 es idéntico al ángulo de dirección $\theta_A$. Para los vectores en el cuarto cuadrante, el ángulo $\theta$ es negativo, lo que significa que para estos vectores, el ángulo de dirección $\theta_A$ se mide en sentido horario desde el eje $x$ positivo. De manera similar, para los vectores en el segundo cuadrante, el ángulo $\theta$ es negativo.
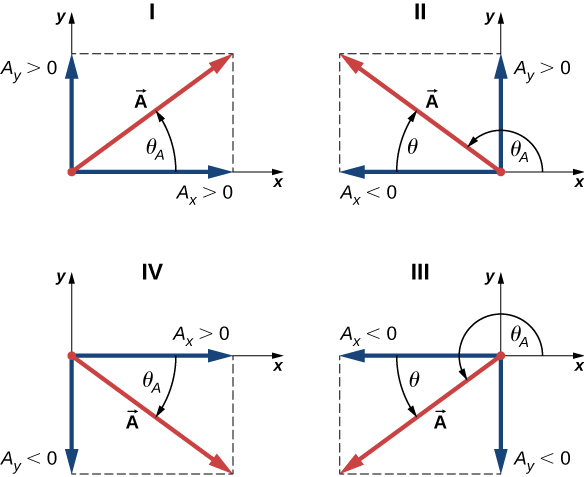
Cuando el vector se encuentra en el segundo o tercer cuadrante, donde el componente $A_x$ es negativo, el ángulo de dirección es $\theta_A = \theta + 180\degree$ (Figura 2.19).
Ejemplo 2.4
Magnitud y dirección del vector de desplazamiento
Se mueve un puntero del ratón sobre el monitor desde su posición inicial en el punto $(6.0 cm, 1.6 cm)$ a un icono ubicado en el punto $(2.0 cm, 4.5 cm)$. ¿Cuál es la magnitud y la dirección del vector de desplazamiento del puntero?
Estrategia
En el ejemplo 2.3, encontramos el vector de desplazamiento $\bold{\vec{D}}$ del puntero del ratón (ver ecuación 2.14). Identificamos sus componentes escalares $D_x = -4.0cm$ y $D_y = + 2.9cm$ y sustituimos en la Ecuación 2.15 y la Ecuación 2.16 para encontrar la magnitud $D$ y la dirección $\theta_D$, respectivamente.
Solución
La magnitud del vector $\bold{\vec{D}}$ es
$D = \sqrt{D_x^2 + D_y^2} = \sqrt{(-4.0 cm)^2 + (2.9 cm)^2}\\ \;\;\;\;= \sqrt{(4.0)^2 + (2.9)^2}\;cm = 4.9\; cm$La dirección del ángulo es:
$tan\;\theta = \frac{D_y}{D_x} = -0.725 \implies \theta = tan^{-1}(-0.725) = −35.9\degree$.El vector $\bold{\vec{D}}$ se encuentra en el segundo cuadrante, por lo que su ángulo de dirección es
$$ \theta_D = \theta + 180\degree = -35.9\degree + 180\degree = 144.1\degree$$ Comprueba tu aprendizaje 2.5
Comprueba tu aprendizaje 2.5
$\bold{\vec{D}} = (- 5.00\^{\bold{i}} - 3.00\^{\bold{j}})\; cm$, encuentra su magnitud y dirección.
En muchas aplicaciones, las magnitudes y direcciones de los vectores son conocidas y necesitamos encontrar la resultante de muchos vectores. Por ejemplo, imagina $400$ autos moviéndose en el Golden Gate Bridge en San Francisco con un fuerte viento. Cada automóvil le da al puente un empuje diferente en varias direcciones y nos gustaría saber qué tan grande puede ser el empuje resultante. Ya hemos adquirido cierta experiencia con la construcción geométrica de las sumas de vectores, por lo que sabemos que la tarea de encontrar la resultante dibujando los vectores y midiendo sus longitudes y ángulos puede volverse intratable, lo que lleva a grandes errores. Las preocupaciones como ésta no aparecen cuando utilizamos métodos analíticos. El primer paso en un enfoque analítico es encontrar componentes vectoriales cuando se conocen la dirección y la magnitud de un vector.
Volvamos al triángulo rectángulo en la Figura 2.18. El cociente del lado $A_x$ adyacente a la hipotenusa $A$ es la función coseno del ángulo $\theta_A, A_x/A = cos\;\theta_A$, y el cociente del lado $A_y$ opuesto a la hipotenusa $A$ es la función seno de $\theta_A, A_y/A = sen\;\theta$.
Cuando se conocen la magnitud $A$ y el ángulo $\theta_A$, podemos resolver estas relaciones para los componentes escalares:
Al calcular los componentes del vector con la Ecuación 2.17, se debe tener cuidado con el ángulo. El ángulo de dirección $\theta_A$ de un vector es el ángulo medido en sentido antihorario desde la dirección positiva en el eje $x$ hasta el vector. La medición en el sentido de las agujas del reloj da un ángulo negativo.
Ejemplo 2.5
Componentes de vectores de desplazamiento
Un grupo de rescate, para un niño desaparecido, sigue a un perro de búsqueda llamado Trooper. Trooper deambula mucho y hace muchos olfateos de prueba a lo largo de muchos caminos diferentes. Trooper eventualmente encuentra al niño y la historia tiene un final feliz, pero sus desplazamientos parecen ser realmente intrincados. En uno de ellos camina $200.0 m$ al sureste, luego corre hacia el norte unos $300.0 m$. En el tercer tramo, examina los olores cuidadosamente durante $50.0 m$ en la dirección $30\degree$ al noroeste. En el cuarto tramo, Trooper va directamente al sur por $80.0 m$, toma aire fresco y gira $23\degree$ al suroeste por $150.0 m$. Encuentra las componentes escalares de los vectores de desplazamiento de Trooper y sus vectores de desplazamiento en forma vectorial para cada tramo.
Estrategia
Adoptemos un sistema de coordenadas rectangular con el eje $x$ positivo en la dirección del este geográfico, con la dirección $y$ positiva apuntada al norte geográfico. Explícitamente, el vector unitario $\^{\bold{i}}$ apunta al este y el vector unitario $\^{\bold{j}}$ apunta al norte. Trooper hace cinco tramos, por lo que hay cinco vectores de desplazamiento. Comenzamos identificando sus magnitudes y ángulos de dirección, luego usamos la Ecuación 2.17 para encontrar los componentes escalares de los desplazamientos y la Ecuación 2.12 para los vectores de desplazamiento.
Solución
En el primer tramo, la magnitud de desplazamiento es $L_1 = 200.0 m$ y la dirección es sureste.
Para el ángulo de dirección $\theta_1$, podemos tomar $45\degree$ medido en el sentido de las agujas del reloj desde la dirección este o $45\degree+ 270\degree$ medido en sentido antihorario desde la dirección este. Con la primera opción, $\theta_1 = -45\degree$. Con la segunda opción, $\theta_1 = + 315\degree$. Podemos usar cualquiera de estos dos ángulos. Lss componentes son
$$L_{1x} = L_1cos\theta_1 = (200.0m)cos315\degree = 141.4m\\ L_{1y} = L_1sen\theta_1 = (200.0m)sen315\degree = -141.4m$$El vector de desplazamiento del primer tramo es
$$\bold{\vec{L}}_1 = L_{1x}\^{\bold{i}} + L_{1y}\^{\bold{j}} =(141.4\^{\bold{i}} - 141.1\^{\bold{j}})m$$En la segunda etapa de las andanzas del Trooper, la magnitud del desplazamiento es $L_2 = 300.0m$ y la dirección es norte.
El ángulo de dirección es $\theta_2 = + 90\degree$. Obtenemos los siguientes resultados:
$$L_{2x} = L_2cos\theta_2 = (300.0)cos90\degree = 0.0\\ L_{2y} = L_2sen\theta_2 = (300.0)sen90\degree = 300.0m\\ \bold{\vec{L}}_2 = L_{2x}\^{\bold{i}} + L_{2y}\^{\bold{j}} = (300.0m)\^{\bold{j}}$$En el tercer tramo, la magnitud del desplazamiento es $L_3 = 50.0 m$ y la dirección es $30\degree$ al noroeste. El ángulo de dirección medido en sentido antihorario desde la dirección este es $\theta_3 = 30\degree + 90\degree = + 120\degree$. Esto da las siguientes respuestas:
$$L_{3x} = L_3cos\theta_3 = (50.0)cos120\degree = -25.0m\\ L_{3y} = L_3sen\theta_3 = (50.0)sen120\degree = +43.3m\\ \bold{\vec{L}}_3 = L_{3x}\^{\bold{i}} + L_{3y}\^{\bold{j}} = (-25.0\^{\bold{i}} + 43.3\^{\bold{j}})m$$En el cuarto tramo de la excursión, la magnitud de desplazamiento es $L_4 = 80.0 m$ y la dirección es sur. El ángulo de dirección se puede tomar como $\theta_4 = -90\degree$ o $\theta_4 = + 270\degree$. Obtenemos
$$L_{4x} = L_4cos\theta_4 = (80.0m)cos(-90\degree) = 0,\\ L_{4y} = L_4sen\theta_4 = (80.0m)sen(-90\degree) = -80m,\\ \bold{\vec{L}}_4 = L_{4x}\^{\bold{i}} + L{4y}\^{\bold{j}} = (-80.0m)\^{\bold{j}}$$En el último tramo, la magnitud es $L_5 = 150.0 m$ y el ángulo es $\theta_5 = -23\degree + 270\degree = + 247\degree$ ($23\degree$ suroeste), que da
$$L_{5x} = L_5cos\theta_5 = (150.0m)cos247\degree = -58.6 m,\\ L_{5y} = L_5sen\theta_5 = (150.0m)sen247\degree = -138.1 m,\\ \bold{\vec{L}}_5 = L_{5x}\^{\bold{i}} + L_{5y}\^{\bold{j}} =(-58.6\^{\bold{i}} -138.1\^{\bold{j}})m$$ Comprueba tu aprendizaje 2.6
Comprueba tu aprendizaje 2.6
Coordenadas polares
Para describir posiciones de puntos o vectores en un plano, necesitamos dos direcciones ortogonales. En el sistema de coordenadas cartesianas, estas direcciones están dadas por los vectores unitarios $\^{\bold{i}}$ y $\^{\bold{j}}$ a lo largo del eje $x$ y el eje $y$, respectivamente. El sistema de coordenadas cartesianas es muy conveniente para describir los desplazamientos y las velocidades de los objetos y las fuerzas que actúan sobre ellos.
Sin embargo, se vuelve engorroso cuando necesitamos describir la rotación de estos objetos. Al describir la rotación, generalmente trabajamos en el sistema de coordenadas polares.
En el sistema de coordenadas polares, la posición del punto $P$ en un plano viene dada por dos coordenadas polares (Figura 2.20). La primera coordenada polar es la coordenada radial $r$, que es la distancia al punto $P$ desde el origen. La segunda coordenada polar es un ángulo $\phi$, que es el vector radial que se forma con alguna dirección elegida, generalmente la dirección positiva de $x$. En coordenadas polares, los ángulos se miden en radianes o $rads$. El vector radial está unido al origen y apunta desde el origen al punto $P$. Esta dirección radial se describe mediante un vector radial unitario $\^{\bold{r}}$. El segundo vector unitario $\^{\bold{t}}$ es un vector ortogonal a la dirección radial $\^{\bold{r}}$.
La dirección positiva $+ \^{\bold{t}}$ indica cómo cambia el ángulo en dirección contraria a las agujas del reloj. De esta manera, un punto $P$ que tiene coordenadas $(x, y)$ en el sistema rectangular se puede describir de manera equivalente en el sistema de coordenadas polares mediante las dos coordenadas polares $(r, \phi)$. La ecuación 2.17 es válida para cualquier vector, por lo que podemos usarlo para expresar las coordenadas $x$ e $y$ del vector $\bold{\vec{r}}$. De esta forma, obtenemos la conexión entre las coordenadas polares y las coordenadas rectangulares del punto $P$,
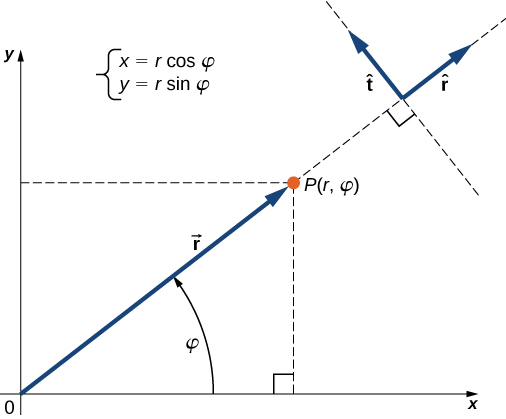
Ejemplo 2.6
Coordenadas polares
Un cazador de tesoros encuentra una moneda de plata en un lugar a $20.0 m$ de distancia de un pozo seco en la dirección $20\degree$ al noreste y encuentra una moneda de oro en un lugar a $10.0 m$ del pozo en la dirección $20\degree$ noroeste. ¿Cuáles son las coordenadas polares y rectangulares de estos hallazgos con respecto al pozo?
Estrategia
El pozo marca el origen del sistema de coordenadas y este es la dirección $+ x$. Identificamos distancias radiales desde las ubicaciones hasta el origen, que son $r_S = 20.0 m$ (para la moneda de plata) y $r_G = 10.0 m$ (para la moneda de oro). Para encontrar las coordenadas angulares, convertimos $20\degree$ a radianes: $20\degree = 20\pi /180 = \pi /9$. Usamos la Ecuación 2.18 para encontrar las coordenadas $x$ e $y $de las monedas.
Solución
La coordenada angular de la moneda de plata es $\phi_S = \pi /9$, mientras que la coordenada angular de la moneda de oro es $\phi_G = \pi - \pi /9 = 8\pi /9$. Por lo tanto, las coordenadas polares de la moneda de plata son $(r_S, \phi_S) = (20.0m, \pi /9)$ y las de la moneda de oro son $(r_G, \phi_G) = (10.0 m, 8\pi /9)$.
Sustituimos estas coordenadas en la ecuación 2.18 para obtener coordenadas rectangulares. Para la moneda de oro, las coordenadas son
Para la moneda de plata, las coordenadas son
$x_S = r_S cos\phi_S = (20.0m)cos8\pi /9 = 18.9m\\ y_S = r_S sen\phi_S = (20.0m)sen8\pi /9 = 16.8m \implies (x_S, y_S) = (18.9m, 16.8m)$Vectores en tres dimensiones
Para especificar la posición de un punto en el espacio, necesitamos tres coordenadas $(x, y, z)$, donde las coordenadas $x$ e $y$ especifican ubicaciones en un plano, y la coordenada $z$ da una posición vertical por encima o debajo del plano. El espacio tridimensional tiene tres direcciones ortogonales, por lo que no necesitamos dos sino tres vectores unitarios para definir un sistema de coordenadas tridimensional. En el sistema de coordenadas cartesianas, los primeros dos vectores unitarios son el vector unitario del eje $x$ $\^{\bold{i}}$ y el del eje $y$ $\^{\bold{j}}$. El tercer vector unitario $\^{\bold{k}}$ es la dirección del eje $z$ (Figura 2.21). El orden en que los ejes están etiquetados, que es el orden en que aparecen los tres vectores unitarios, es importante pues define la orientación del sistema de coordenadas. El orden $x-y-z$, que es equivalente al orden $\^{\bold{i}} - \^{\bold{j}} - \^{\bold{k}}$, define el sistema de coordenadas según la regla de la mano derecha (orientación positiva).
En el espacio tridimensional, el vector $\bold{\vec{A}}$ tiene tres componentes de vector: el componente $\bold{\vec{A}}_x = A_x\^{\bold{i}}$, que es la parte del vector $\bold{\vec{A}}$ a lo largo del eje $x$; el componente $y$ $\bold{\vec{A}}_y = A_y\^{\bold{j}}$, que es la parte de $\bold{\vec{A}}$ a lo largo del eje $y$; y el componente $z$ $\bold{\vec{A}}_z = A_z\^{\bold{k}}$, que es la parte del vector a lo largo del eje $z$.
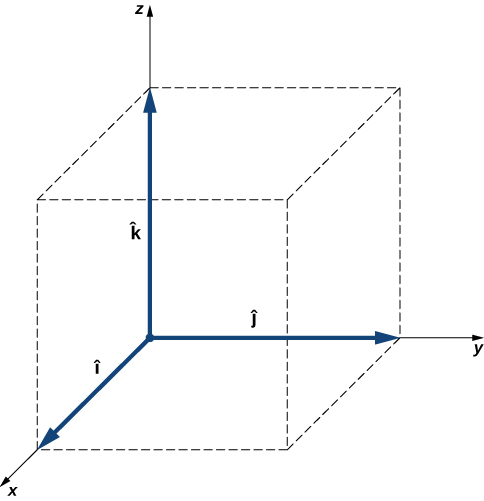
Un vector en el espacio tridimensional es la suma del vector de sus tres componentes del vector (Figura 2.22):
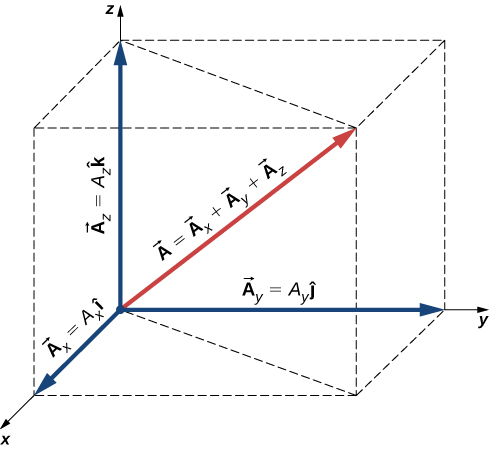
En la siguiente escena interactiva, diseñada por Ángela Nuñez Castaín, puedes cambiar los valores $A_x, A_y$ y $A_z$, denotados en la escena como $a, b$ y $c$ respectivamente. Observa la posición del vector $\bold{\vec{V}}$ luego de realizar los cambios. Puedes rotar la escena con clic izquierdo sostenido.
Si conocemos las coordenadas de su origen $b\; (x_b, y_b, z_b)$ y de su extremo $e\; (x_e, y_e, z_e)$, se obtienen sus componentes escalares tomando sus diferencias: $A_x$ y $A_y$ están dados por la ecuación 2.13 y el componente $z$ está dado por
La magnitud $A$ se obtiene al generalizar la Ecuación 2.15 a tres dimensiones:
$$A = \sqrt{A_x^2 + A_y^2 + A_z^2}\tag{2.21}$$Esta expresión para la magnitud del vector proviene de aplicar el teorema de Pitágoras dos veces. Como se ve en la Figura 2.22, la diagonal en el plano $xy$ tiene una longitud $\sqrt{A_x^2 + A_y^2}$ y su cuadrado se suma al cuadrado $A_z^2$ para dar $A^2$
Ten en cuenta que cuando el componente $z$ es cero, el vector se encuentra completamente en el plano $xy$ y su descripción se reduce a dos dimensiones.
Ejemplo 2.7
Despegue de un Drone
Durante un despegue de IAI Heron (Figura 2.23), su posición con respecto a una torre de control es de $100 m$ sobre el suelo, $300 m$ hacia el este y $200 m$ hacia el norte. Un minuto más tarde, su posición es de $250 m$ sobre el suelo, $1200 m$ al este y $2100 m$ al norte. ¿Cuál es el vector de desplazamiento del dron con respecto a la torre de control? ¿Cuál es la magnitud de su vector de desplazamiento?
Estrategia
Tomamos el origen del sistema de coordenadas cartesianas como la torre de control.

La dirección del eje $+ x$ viene dada por el vector unitario $\^{\bold{i}}$ al este, la dirección del eje $+ y$ está dada por el vector unitario $\^{\bold{j}}$ al norte, y la dirección del eje $+ z$ viene dada por vector unitario $\^{\bold{k}}$, que apunta hacia arriba desde el suelo. La primera posición del dron es el origen (o, de manera equivalente, el comienzo) del vector de desplazamiento y su segunda posición es el final del vector de desplazamiento.
Solución
Identificamos: $$b\; (300.0 m, 200.0 m, 100.0 m)\\e \;(480.0 m, 370.0 m, 250.0 m),$$ usamos la Ecuación 2.13 y la Ecuación 2.20 para encontrar los componentes escalares del vector de desplazamiento del dron:
$D_x = x_e − x_b = 1200.0 m − 300.0 m = 900.0 m,\\ D_y = y_e − y_b = 2100.0 m − 200.0 m = 1900.0 m,\\ D_z = z_e − z_b = 250.0 m − 100.0 m = 150.0 m.$
Sustituimos estas componentes en la Ecuación 2.19 para encontrar el vector de desplazamiento:
$$\begin{split} \bold{\vec{D}} &= D_x\^{\bold{i}} + D_y\^{\bold{j}} + D_z\^{\bold{k}}\\ &= 900.0m\^{\bold{i}} + 1900.0m\^{\bold{j}} + 150.0m\^{\bold{k}}\\ &= (0.90\^{\bold{i}} + 1.90\^{\bold{j}} + 0.15\^{\bold{k}})km. \end{split}$$Sustituimos en la Ecuación 2.21 para encontrar la magnitud del desplazamiento:
$$\begin{split} D &= \sqrt{D_x^2 + D_y^2 + D_z^2}\\ &= \sqrt{(0.90km)^2 + /1.90km)^2 + (0.15km)^2}\\ &= 4.4km \end{split}$$ Comprueba tu aprendizaje 2.7
Comprueba tu aprendizaje 2.7
¿Cuál es la magnitud del vector de velocidad del dron?
Algebra vectorial
Los vectores se pueden sumar y multiplicar por escalares. La suma de vectores es asociativa (ecuación 2.8) y conmutativa (ecuación 2.7), y la multiplicación vectorial por una suma de escalares es distributiva (ecuación 2.9). Además, la multiplicación escalar por una suma de vectores es distributiva:
$$\alpha(\bold{\vec{A}} + \bold{\vec{B}}) =\alpha\bold{\vec{A}} + \alpha\bold{\vec{B}}\tag{2.22}$$En esta ecuación, $\alpha$ es cualquier número (un escalar). Por ejemplo, un vector antiparalelo al vector $\bold{\vec{A}} = A_x\^{\bold{i}} + A_y\^{\bold{j}} + A_z\^{\bold{k}}$ puede expresarse simplemente multiplicando $\bold{\vec{A}}$ por el escalar $\alpha = -1$:
$$-\bold{\vec{A}} = -A_x\^{\bold{i}} - A_y\^{\bold{j}} - A_z\^{\bold{k}}\tag{2.23}$$Ejemplo 2.8
Dirección del movimiento
En un sistema de coordenadas cartesianas donde $\^{\bold{i}}$ denota el este geográfico, $\^{\bold{j}}$ denota el norte geográfico, y $\^{\bold{k}}$ denota la altitud sobre el nivel del mar, un convoy militar avanza su posición a través de territorio desconocido con velocidad $\bold{\vec{v}} = (4.0\^{\bold{i}} + 3.0\^{\bold{j}} + 0.1\^{\bold{k}}) km/h$. Si el convoy tuviera que retirarse, ¿en qué dirección geográfica lo haría?
Solución
El vector de velocidad tiene el tercer componente $\bold{\vec{v}}_z = (+ 0.1km/h)\^{\bold{k}}$, que dice que el convoy está escalando a un ritmo de $100 m/h$ a través de terreno montañoso.
Al mismo tiempo, su velocidad es de $4.0 km/h $hacia el este y $3.0 km/h$ hacia al norte, por lo que se mueve en el suelo en la dirección $tan^{-1} (3/4) \approx 37\degree$ al noreste. Si el convoy tuvo que retirarse, su nuevo vector de velocidad $\bold{\vec{u}}$ tendría que ser antiparalelo a $\bold{\vec{v}}$ de tal forma que $\bold{\vec{u}} = -\alpha\bold{\vec{v}}$, donde $\alpha$ es un número positivo. Por lo tanto, la velocidad del retroceso sería $\bold{\vec{u}} = \alpha(-4.0\^{\bold{i}} - 3.0\^{\bold{j}} - 0.1\^{\bold{k}}) km/h$. El signo negativo de la tercera componente indica que el convoy estaría descendiendo. El ángulo de dirección de la velocidad de retroceso es $tan^{-1}(-3\alpha/-4\alpha) \approx 37\degree$ suroeste. Por lo tanto, el convoy se movería en el suelo en dirección $37\degree$ al suroeste, mientras desciende en su camino de regreso.
El vector con valor cero en el álgebra vectorial se llama vector nulo, denotado por $\bold{\vec{0}}$. Todos los componentes del vector nulo son cero,
$\bold{\vec{0}} = 0\^{\bold{i}} + 0\^{\bold{j}} + 0\^{\bold{k}}$, entonces el vector nulo no tiene longitud ni dirección. Dos vectores $\bold{\vec{A}}$ y $\bold{\vec{B}}$ son vectores iguales si y solo si su diferencia es el vector nulo:
Esta ecuación vectorial significa que debemos tener simultáneamente $A_x - B_x = 0, A_y - B_y = 0$ y $A_z - B_z = 0$.
Por lo tanto, podemos escribir $\bold{\vec{A}} = \bold{\vec{B}}$ sí y solo si los componentes correspondientes de los vectores $\bold{\vec{A}}$ y $\bold{\vec{B}}$ son iguales:
Dos vectores son iguales cuando sus correspondientes componentes escalares son iguales. Resolver vectores en sus componentes escalares (es decir, encontrar sus componentes escalares) y expresarlos analíticamente en la forma vectorial (dada por la Ecuación 2.19) nos permite usar el álgebra vectorial para encontrar sumas o diferencias de muchos vectores analíticamente (es decir, sin usar métodos gráficos). Por ejemplo, para encontrar la resultante de dos vectores $\bold{\vec{A}}$ y $\bold{\vec{B}}$, simplemente los sumamos componente por componente, de la siguiente manera:
$$\begin{split} \bold{\vec{R}} &= \bold{\vec{A}} + \bold{\vec{B}}\\ &= (A_x\^{\bold{i}} + A_y\^{\bold{j}} +A_z\^{\bold{k}}) + (B_x\^{\bold{i}} + B_y\^{\bold{j}} +B_z\^{\bold{k}})\\ &= (A_x + B_x)\^{\bold{i}} + (A_y + B_y)\^{\bold{j}} + (A_z + B_z)\^{\bold{k}} \end{split}$$De esta manera, usando la Ecuación 2.24, los componentes escalares del vector resultante $\bold{\vec{R}} = R_x\^{\bold{i}} + R_y\^{\bold{j}} + R_z\^{\bold{k}}$ son las sumas de los componentes escalares correspondientes de los vectores $\bold{\vec{A}}$ y $\bold{\vec{B}}$:
$$\begin{cases} R_x = A_x + B_x\\ R_y = A_y + B_y\\ R_z = A_z + B_z \end{cases}$$Los métodos analíticos pueden usarse para encontrar componentes de la resultante de muchos vectores. Por ejemplo, si vamos a sumar $N$ vectores $\bold{\vec{F}}_1, \bold{\vec{F}}_2, \bold{\vec{F}}_3, \dots, \bold{\vec{F}}_N$, donde cada vector es $\bold{\vec{F}}_k = F_{kx}\^{\bold{i}} + F_{ky}\^{\bold{j}} + F_{kz}\^{\bold{k}}$, el vector resultante $\bold{\vec{F}}_R$ es
Por lo tanto, los componentes escalares del vector resultante son
$$\begin{cases} F_{Rx} = \displaystyle{\sum_{k=1}^N} F_{kx} = F_{1x} + F_{2x} +\dots + F_{Nx}\\ F_{Ry} = \displaystyle{\sum_{k=1}^N} F_{ky} = F_{1y} + F_{2y} +\dots + F_{Ny}\\ F_{Rz} = \displaystyle{\sum_{k=1}^N} F_{kz} = F_{1z} + F_{2z} +\dots + F_{Nz}\tag{2.25} \end{cases}$$Una vez encontrados los componentes escalares, podemos escribir la resultante en forma vectorial:
$$\bold{\vec{F}}_R = F_{Rx}\^{\bold{i}} + F_{Ry}\^{\bold{j}} + F_{Rz}\^{\bold{k}}$$Los métodos analíticos para encontrar el resultado y, en general, para resolver ecuaciones de vectores son muy importantes en física porque muchas cantidades físicas son vectores. Por ejemplo, usamos este método en cinemática para encontrar la resultante de vectores de desplazamiento resultante y vectores de velocidad, en mecánica para encontrar la resultante de vectores fuerza, en electricidad y magnetismo para encontrar campos eléctricos o magnéticos.
Ejemplo 2.9
Cálculo analítico de una resultante
Tres vectores de desplazamiento $\bold{\vec{A}},\bold{\vec{B}}$ y $\bold{\vec{A}}$ en un plano (Figura 2.13) se especifican por sus magnitudes $A = 10.0, B = 7.0$ y $C = 8.0$, respectivamente, y por sus respectivos ángulos de dirección con la horizontal dirección $\alpha = 35\degree, \beta = -110\degree$ y $\gamma = 30\degree$. Las unidades físicas de las magnitudes son centímetros. Descomponer los vectores en sus componentes escalares y encontrar las siguientes sumas: (a) $\bold{\vec{R}} = \bold{\vec{A}} + \bold{\vec{B}} + \bold{\vec{C}}$ (b) $\bold{\vec{D}} = \bold{\vec{A}} - \bold{\vec{B}}$ y (c) $\bold{\vec{S}}= \bold{\vec{A}} - 3\bold{\vec{B}}+ \bold{\vec{C}}$
Estrategia
Primero, usamos la Ecuación 2.17 para encontrar los componentes escalares de cada vector y luego expresamos cada vector en su forma de componentes vectoriales dada por la Ecuación 2.12. Luego, usamos métodos analíticos de álgebra vectorial para encontrar las resultantes.
Solución
Descomponemos los vectores dados en sus componentes escalares:
$$\begin{cases} A_x =A\;cos\alpha =(10.0cm)cos35\degree = 8.19cm\\ A_y =A\;sen\alpha =(10.0cm)sen35\degree = 5.73cm \end{cases}$$ $$\begin{cases} B_x =B\;cos\beta =(7.0cm)cos(-110\degree) = -2.39cm\\ B_y =B\;sen\beta =(7.0cm)sen(-110\degree) = -6.58cm \end{cases}$$ $$\begin{cases} C_x =C\;cos\gamma =(8.0cm)cos30\degree = 6.93cm\\ C_y =C\;sen\gamma =(8.0cm)sen30\degree = 4.00cm \end{cases}$$Para (a) podemos sustituir directamente en la Ecuación 2.24, para encontrar los componentes escalares de la resultante:
$$R_x = A_x + B_x + C_x = 8.19 cm - 2.39 cm + 6.93 cm = 12.73 cm\\ R_y = A_y + B_y + C_y = 5.73 cm - 6.58 cm + 4.00 cm = 3.15 cm$$Por lo tanto, el vector resultante $\bold{\vec{R}}$ es:
$R_x\^{\bold{i}} + R_y\^{\bold{j}} = (12.7\^{\bold{i}} + 3.1\^{\bold{j}})cm$.
Para (b), podemos escribir la diferencia del vector como
$$\bold{\vec{D}} = \bold{\vec{A}} - \bold{\vec{B}} = (A_x - B_x)\^{\bold{i}} +(A_y - B_y)\^{\bold{j}}$$Entonces, los componentes escalares de la diferencia vectorial son
$$D_x = A_x - B_x = 8.19 cm - (-2.39) cm = 10.58 cm\\ D_y = A_y - B_y = 5.73 cm - (-6.58) cm = 12.31 cm$$Por lo tanto, el vector de diferencia es $\bold{\vec{D}} = D_x\^{\bold{i}} + D_y\^{\bold{j}} = (10.6\^{\bold{i}} + 12.3\^{\bold{j}}) cm$
Para (c), podemos escribir el vector $\bold{\vec{S}}$ en la siguiente forma explícita:
$$\begin{split} \bold{\vec{S}} &= \bold{\vec{A}} -3\bold{\vec{B}} + \bold{\vec{C}}\\ &= (A_x\^{\bold{i}} + A_y\^{\bold{j}}) - 3(B_x\^{\bold{i}} + B_y\^{\bold{j}}) + (C_x\^{\bold{i}} + C_y\^{\bold{j}})\\ &= (A_x - 3B_x + C_x)\^{\bold{i}} + (A_y - 3B_y + C_y)\^{\bold{j}} \end{split}$$Entonces, los componentes escalares de $\bold{\vec{S}}$ son
$$\begin{split} S_x &= A_x − 3B_x + C_x \\ &= 8.19 cm − 3(−2.39 cm) + 6.93 cm\\ &= 22.29 cm \end{split}$$El vector $\bold{\vec{S}} = S_x\^{\bold{i}} + S_y\^{\bold{j}} = (22.3\^{\bold{i}} + 29.5\^{\bold{j}}) cm$
Explicación
Una vez encontrados los componentes del vector, podemos ilustrar los vectores mediante gráficos o podemos calcular magnitudes y ángulos de dirección, como se muestra en la Figura 2.24. Los resultados para las magnitudes en (b) y (c) se pueden comparar con resultados para los mismos problemas obtenidos con el método gráfico, que se muestran en la Figura 2.14 y la Figura 2.15.
Ten en cuenta que el método analítico produce resultados exactos y su precisión no está limitada por la resolución de una regla o un transportador, como lo fue con el método gráfico utilizado en el Ejemplo 2.2 para encontrar esta misma resultante.
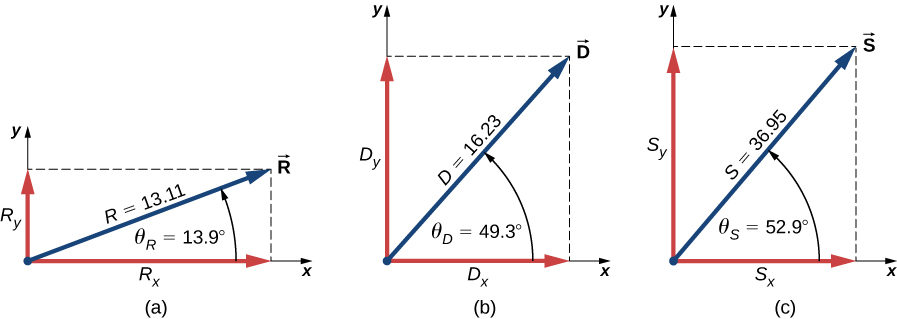
 Comprueba tu aprendizaje 2.8
Comprueba tu aprendizaje 2.8
Ejemplo 2.10
El juego del tira y afloja
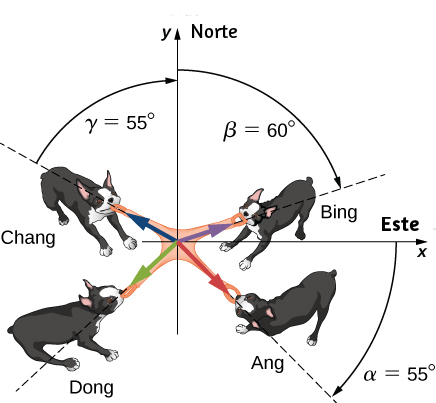
Cuatro perros llamados Ang, Bing, Chang y Dong juegan un juego de tira y afloja con un juguete (Figura 2.25). Ang se tira del juguete en dirección $\alpha = 55\degree$ al sureste, Bing tira en dirección $\beta = 60\degree$ al noreste, y Chang tira en dirección $\gamma = 55\degree$ al noroeste.
Ang tira fuertemente con $160.0$ unidades de fuerza ($N$), que abreviamos como $A = 160.0 N$. Bing tira incluso más fuerte que Ang con una fuerza de magnitud $B = 200.0 N$, y Chang tira con una fuerza de magnitud $C = 140.0 N$. Cuando Dong tira del juguete de tal manera que su fuerza equilibra la resultante de las otras tres fuerzas, el juguete no se mueve en ninguna dirección. ¿Con qué fuerza y en qué dirección debe Dong tirar del juguete para que esto suceda?
Estrategia
Suponemos que el este es la dirección del eje $x$ positivo y el norte es la dirección del eje $y$ positivo. Como en el ejemplo 2.9, tenemos que descomponer las tres fuerzas dadas:
$\bold{\vec{A}}$ (tracción de Ang), $\bold{\vec{B}}$ (tracción de Bing) y $\bold{\vec{C}}$ (tracción de Chang), en sus componentes escalares y luego encontrar los componentes escalares del vector resultante $\bold{\vec{R}} = \bold{\vec{A}} + \bold{\vec{B}} + \bold{\vec{C}}$. Cuando la fuerza de tracción $\bold{\vec{D}}$ de Dong equilibra esta resultante, la suma de $\bold{\vec{D}}$ y $\bold{\vec{R}}$ debe dar el vector nulo $\bold{\vec{D}} + \bold{\vec{R}} = 0$. Esto significa que $\bold{\vec{D}} = - \bold{\vec{R}}$, entonces la tracción de Dong debe ser antiparalelo a $\bold{\vec{R}}$
Solución
Los ángulos de dirección son $\theta_A = -\alpha = -55\degree, \theta_B = 90\degree - \beta = 30\degree$, y $θ\theta_C = 90\degree + \gamma = 145\degree$, sustituyéndolos en la ecuación 2.17 nos da los componentes escalares de las tres fuerzas dadas:
Ahora calculamos los componentes escalares del vector resultante: $\bold{\vec{R}}= \bold{\vec{A}} + \bold{\vec{B}} + \bold{\vec{C}}$.
$$R_x = A_x + B_x + C_x = +91.8 N + 173.2 N − 114.7 N = +150.3N\\ R_y = A_y + B_y + C_y = −131.1 N + 100.0 N + 80.3 N = +49.2N$$El vector antiparalelo a la resultante $\bold{\vec{R}}$es:
$$\bold{\vec{D}} = -\bold{\vec{R}} = -R_x\^{\bold{i}} - R_y\^{\bold{j}} = (-150.3\^{\bold{i}} - 49.2\^{\bold{j}}) N$$La magnitud de la fuerza de tracción de Dong es
$$\begin{split} D &= \sqrt{D_x^2 + D_y^2}\\ &= \sqrt{(-150.3)^2 + (-49.2)^2}N\\ &= 158.1 N \end{split}$$La dirección de la fuerza de tracción de Dong es
$$\theta = tan^{-1}\Big(\frac{D_y}{D_x}\Big) = tan^{-1}\Big(\frac{-49.2N}{-150.3N}\Big) = 18.1\degree$$Dong tira en la dirección $18.1\degree$ suroeste porque ambos componentes son negativos, lo que significa que el vector de tracción se encuentra en el tercer cuadrante (Figura 2.19).
 Comprueba tu aprendizaje 2.9
Comprueba tu aprendizaje 2.9
Ejemplo 2.11
Encuentra la magnitud del vector $\bold{\vec{C}}$ que satisface la ecuación
$2\bold{\vec{A}} - 6\bold{\vec{B}} + 3\bold{\vec{C}} = 2\^{\bold{j}}$,
donde $\bold{\vec{A}} = \^{\bold{i}} - 2\^{\bold{k}}$ y $\bold{\vec{B}} = -\^{\bold{j}} + \^{\bold{k}}/2$.
Estrategia
Primero resolvemos la ecuación dada para el vector desconocido $\bold{\vec{C}}$. Luego sustituimos $\bold{\vec{A}}$ y $\bold{\vec{B}}$, agrupamos los términos a lo largo de cada una de las tres direcciones $\^{\bold{i}}, \^{\bold{j}}$ y $\^{\bold{k}}$ e identifícamos los componentes escalares $C_x, C_y$ y $C_z$. Finalmente, sustituimos en la ecuación 2.21 para encontrar la magnitud $C$.
Los componentes son $C_x = -2/3, C_y = -4/3$, y $C_z = 7/3$, sustituyendo en la Ecuación 2.21 obtenemos
$$\begin{split} C&= \sqrt{C_x^2 + C_y^2 + C_z^2}\\ &= \sqrt{(-2/3)^2 + (-4/3)^2 + (7/3)^2}\\ &= \sqrt{\frac{23}{3}} \end{split}$$Ejemplo 2.12
Desplazamiento de un esquiador
Comenzando en una estación de esquí, un esquiador de fondo recorre $5.0 km$ al norte, luego $3.0 km$ al oeste, y finalmente $4.0 km$ al suroeste antes de tomar un descanso. Encuentre su vector de desplazamiento total relativo al refugio cuando se encuentre en el punto de descanso. ¿Cuán lejos y en qué dirección debe esquiar desde el punto de descanso para regresar directamente al albergue?
Estrategia
Suponemos un sistema de coordenadas rectangulares con el origen en la estación de esquí y con el vector unitario $\^{\bold{i}}$ apuntando al este y el vector unitario $\^{\bold{j}}$ apuntando al norte. Hay tres desplazamientos: $\bold{\vec{D}}_1, \bold{\vec{D}}_2$ y $\bold{\vec{D}}_3$. Identificamos sus magnitudes como $D_1 = 5.0 km, D_2 = 3.0 km$, y $D_2 = 4.0 km$. Identificamos sus direcciones como los ángulos $\theta_1 = 90\degree, \theta_2 = 180\degree$, y $\theta_3 = 180\degree + 45\degree = 225\degree$. Descomponemos cada vector de desplazamiento en sus componentes escalares y sustituimos las componentes en la ecuación 2.24 para obtener las componentes escalares del desplazamiento resultante $\bold{\vec{D}}$ desde el alojamiento hasta el punto de descanso.
En el camino de regreso desde el punto de descanso hasta la cabaña, el desplazamiento es $\bold{\vec{B}} = -\bold{\vec{D}}$. Finalmente, encontramos la magnitud y dirección de $\bold{\vec{B}}$.
Solución
Los componentes escalares de los vectores de desplazamiento resultante son
$$\begin{cases} D_{1x} = D_1cos\theta_1 = (5.0km)cos(90\degree) = 0\\ D_{1y} = D_1sen\theta_1 = (5.0km)sen(90\degree) = 5.0km \end{cases}$$ $$\begin{cases} D_{2x} = D_2cos\theta_2 = (3.0km)cos(180\degree) = -3.0km\\ D_{2y} = D_2sen\theta_2 = (3.0km)sen(180\degree) = 0 \end{cases}$$ $$\begin{cases} D_{3x} = D_3cos\theta_3 = (4.0km)cos(225\degree) = -2.8km\\ D_{3y} = D_3sen\theta_3 = (4.0km)sen(225\degree) = 2.8kmkm \end{cases}$$Los componentes escalares del vector de desplazamiento son
$$D_x = D_{1x} + D_{2x} + D_{3x} = (0 −3.0 −2.8)km = −5.8 km\\ D_y = D_{1y} + D_{2y} + D_{3y} = (5.0 + 0 −2.8) km = +2.2 km$$Por lo tanto, el vector de desplazamiento resultante del esquiador es
$$\bold{\vec{D}} = D_x\^{\bold{i}} + D_y\^{\bold{j}} = (- 5.8\^{\bold{i}} + 2.2\^{\bold{j}}) km$$En el camino de regreso a la cabaña, su desplazamiento es
$$\bold{\vec{B}} = \bold{\vec{D}} = - (- 5.8\^{\bold{i}} + 2.2\^{\bold{j}}) km = (5.8\^{\bold{i}} - 2.2\^{\bold{j}}) km$$Su magnitud es
$$\begin{split} B&= \sqrt{B_x^2 + By^2}\\ &= \sqrt{(5.8)^2 + (-2.8)^2}\\ &= 6.2\;km \end{split}$$Su ángulo de dirección es $\theta = tan^{-1}(-2.2/5.8) = - 20.8\degree$. Por lo tanto, para regresar a la cabaña, debe recorrer $6.2 km$ en una dirección de aproximadamente $21\degree$ al sureste.
Explicación
Ten en cuenta que no se necesita ninguna figura para resolver este problema mediante el método analítico. Se requieren figuras cuando se usa un método gráfico; sin embargo, podemos verificar si nuestra solución tiene sentido al esbozarla, lo cual es un paso final útil para resolver cualquier problema de vectores.
Ejemplo 2.13
Desplazamiento de un Trotador
Un trotador corre por un tramo de $200$ pasos idénticos hasta la cima de una colina y luego trota a lo largo de la cima de la colina $50.0 m$ antes de detenerse en un bebedero (Figura 2.26). Su vector de desplazamiento desde el punto A en la parte inferior de los escalones hasta el punto B en la fuente es $\bold{\vec{D}}_{AB} = (- 90.0\^{\bold{i}} + 30.0\^{\bold{j}}) m$.
¿Cuál es la altura y el ancho de cada paso en la trayecoria?
¿Cuál es la distancia real que cubre el trotador?
Si hace un bucle y vuelve al punto $A$, ¿cuál es su vector de desplazamiento resultante?
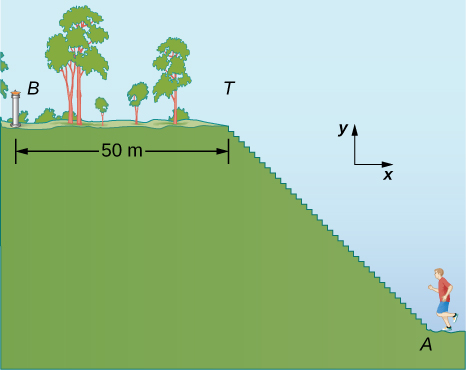
Estrategia
El vector de desplazamiento $\bold{\vec{D}}_{AB}$ es la suma vectorial del vector de desplazamiento $\bold{\vec{D}}_{AT}$ del trotador a lo largo de las escaleras (desde el punto $A$ al final de las escaleras hasta el punto $T$ en la parte superior de las escaleras) y su vector de desplazamiento $\bold{\vec{D}}_{TB}$ en la cima de la colina (desde el punto $T$ en la parte superior de las escaleras hasta la fuente en el punto $B$). Debemos encontrar los componentes horizontal y vertical de $\bold{\vec{D}}_{TB}$. Si cada paso tiene ancho $w$ y altura $h$, el componente horizontal de $\bold{\vec{D}}_{TB}$ debe tener una longitud de $200w$ y el componente vertical debe tener una longitud de $200h$.
La distancia real que recorre el corredor es la suma de la distancia que corre por las escaleras y la distancia de $50.0 m$ que corre a lo largo de la cima de la colina.
Solución
En el sistema de coordenadas indicado en la figura 2.26, el vector de desplazamiento del trotador en la cima de la colina es
$\bold{\vec{D}}_{TB} = (- 50.0 m)\^{\bold{i}}$. Su vector de desplazamiento resultante es:
Por lo tanto, el vector de desplazamiento $\bold{\vec{D}}_{TB}$ a lo largo de las escaleras es
$$\begin{split} \bold{\vec{D}}_{AT} &= \bold{\vec{D}}_{AB} - \bold{\vec{D}}_{TB}\\ &= (−90.0\^{\bold{i}} + 30.0\^{\bold{j}}) m − (−50.0 m)\^{\bold{i}}\\ &= [(−90.0 + 50.0)\^{\bold{i}} + 30.0\^{\bold{j}}] m\\ &= (−40.0\^{\bold{i}} + 30.0\^{\bold{j}}) m \end{split}$$Sus componentes escalares son $D_{ATx} = -40.0m$ y $D_{ATy} = 30.0 m$. Por lo tanto, debemos tener
$$200w = |−40.0| m\text{ y } 200h = 30.0 m$$Entonces, el ancho del paso es $w = 40.0 m/200 = 0.2 m = 20 cm$, y la altura del paso es $w = 30.0 m/200 = 0.15 m = 15 cm$. La distancia que recorre el corredor a lo largo de las escaleras es
$$D_{AT} = \sqrt{D_{ATx}^2 + D_{ATy}^2} = \sqrt{(-40.0)^2 + (30.0)^2} m = 50.0 m$$Por lo tanto, la distancia real que ejecuta es $D_{AT} + D_{TB} = 50.0 m + 50.0 m = 100.0 m$. Cuando hace un bucle y regresa de la fuente a su posición inicial en el punto A, la distancia total que cubre es el doble de esta distancia, $200.0 m$. Sin embargo, su vector de desplazamiento resultante es cero, porque cuando su posición final es la misma que su posición inicial, las componentes escalares de su vector de desplazamiento resultante son cero (ecuación 2.13).
En muchas situaciones físicas, a menudo necesitamos saber la dirección de un vector. Por ejemplo, podemos querer saber la dirección de un vector de campo magnético en algún punto o la dirección del movimiento de un objeto. Ya dijimos que la dirección viene dada por un vector unitario, que es una entidad adimensional, es decir, no tiene unidades físicas asociadas. Cuando el vector en cuestión se encuentra a lo largo de uno de los ejes en un sistema cartesiano de coordenadas, la respuesta es simple, porque entonces su unidad de vector de dirección es paralela o antiparalela a la dirección del vector unitario de un eje. Por ejemplo, la dirección del vector $\bold{\vec{d}}= -5 m\^{\bold{i}}$ es el vector unitario $\bold{\vec{d}}= -\^{\bold{i}}$. La regla general para encontrar el vector unitario de dirección $\^{\bold{V}}$ para cualquier vector $\bold{\vec{d}} $ es dividirlo por su magnitud $V$:
Vemos a partir de esta expresión que el vector de dirección unitaria es de hecho adimensional porque el numerador y el denominador en la ecuación 2.26 tienen la misma unidad física. De esta manera, la Ecuación 2.26 nos permite expresar el vector de dirección unitaria en términos de vectores unitarios de los ejes. El siguiente ejemplo ilustra este principio.
Ejemplo 2.14
Dirección del vector unitario
Si el vector de velocidad del convoy militar del ejemplo 2.8 es $$\bold{\vec{v}} = (4.000\^{\bold{i}} + 3.000\^{\bold{j}} + 0.100\^{\bold{k}}) km/h$$, ¿cuál es el vector unitario en la dirección del movimiento?
Estrategia
El vector unitario en la dirección de movimiento del convoy es el vector $\bold{\vec{v}}$ que es paralelo al vector de velocidad. El vector unitario se obtiene al dividir un vector por su magnitud, de acuerdo con la Ecuación 2.26.
Solución
La magnitud del vector $\bold{\vec{v}}$ es
Para obtener el vector unitario $\^{\bold{v}}$, dividimos $\bold{\vec{v}}$ por su magnitud:
$$\begin{split} \^{\bold{v}} &= \frac{\bold{\vec{v}}}{v} = \frac{(4.000\^{\bold{i}} + 3.000\^{\bold{j}} + 0.001\^{\bold{k}}) km/h}{5.001 km/h}\\ &=(79.98\^{\bold{i}} + 59.99\^{\bold{j}} + 2.00\^{\bold{k}})\times 10^{-2} \end{split}$$Explicación
Ten en cuenta que al utilizar el método analítico con una calculadora, es recomendable llevar a cabo sus cálculos al menos a tres decimales y luego redondear la respuesta final al número requerido de cifras significativas, que es la forma en que realizamos los cálculos en este ejemplo . Si redondeas tu respuesta parcial demasiado pronto, te arriesgas a que tu respuesta final tenga un gran error numérico, y puede estar muy lejos de la respuesta exacta o de un valor medido en un experimento.
 Comprueba tu aprendizaje 2.10
Comprueba tu aprendizaje 2.10
Productos de Vectores
Un vector se puede multiplicar por otro vector pero no se puede dividir por otro vector. Hay dos tipos de productos de vectores usados ampliamente en física e ingeniería. Un tipo de multiplicación es una multiplicación escalar de dos vectores. Tomar un producto escalar de dos vectores da como resultado un número (un escalar), como su nombre lo indica. Los productos escalares se utilizan para definir las relaciones de trabajo y energía. Por ejemplo, el trabajo que una fuerza (un vector) realiza en un objeto mientras causa su desplazamiento (un vector) se define como un producto escalar del vector fuerza con el vector desplazamiento. Un tipo de multiplicación bastante diferente es una multiplicación vectorial de vectores. Tomar un producto vectorial de dos vectores devuelve como resultado un vector, como su nombre lo sugiere. Los productos de vectores se utilizan para definir otras cantidades de vectores derivados. Por ejemplo, al describir las rotaciones, una cantidad vectorial llamada par se define como un producto vectorial de una fuerza aplicada (un vector) y su distancia desde el pivote a la fuerza (un vector). Es importante distinguir entre estos dos tipos de multiplicaciones de vectores porque el producto escalar es una cantidad escalar y un producto vectorial es una cantidad vectorial.
El producto escalar de dos vectores (Producto Punto)
El producto escalar $\bold{\vec{A}}\cdot \bold{\vec{B}}$ de dos vectores es un número definido por la ecuación
$$\bold{\vec{A}}\cdot \bold{\vec{B}} = ABcos\phi\tag{2.27}$$donde $\phi$ es el ángulo entre los vectores (que se muestra en la Figura 2.27). El producto escalar también se denomina producto punto debido a la notación dada.
En la definición del producto escalar, la dirección del ángulo $\phi$ no importa, y se puede medir desde cualquiera de los dos vectores a la otra porque $cos\phi = cos (-\phi) = cos (2\pi-\phi)$. El producto escalar es un número negativo cuando $90\degree \lt \phi \lt 180\degree$ y es un número positivo cuando $0\degree \lt \phi \lt 90\degree$. Además, el producto escalar de dos vectores paralelos es $\bold{\vec{A}}\cdot \bold{\vec{B}} = ABcos0\degree = AB$, y el producto escalar de dos vectores antiparalelos es $\bold{\vec{A}}\cdot \bold{\vec{B}} = ABcos180\degree = -AB$. El producto escalar de dos vectores ortogonales desaparece: $\bold{\vec{A}}\cdot \bold{\vec{B}}= ABcos90\degree = 0$.
El producto escalar de un vector consigo mismo es el cuadrado de su magnitud:
$$\bold{\vec{A}}^2 \equiv \bold{\vec{A}}\cdot \bold{\vec{A}} = AAcos0 = A^2\tag{2.28}$$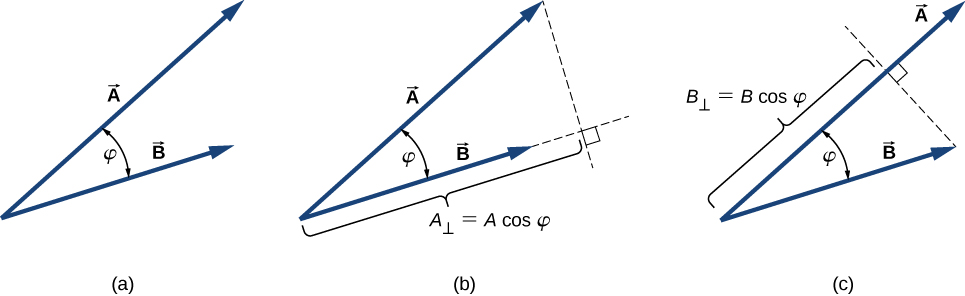
Ejemplo 2.15
El producto punto. Para los vectores mostrados en la Figura 2.13, encuentra el producto escalar $\bold{\vec{A}}\cdot \bold{\vec{F}}$
Estrategia
De la figura 2.13, las magnitudes de los vectores $\bold{\vec{A}}$ y $\bold{\vec{F}}$ son $A = 10.0$ y $F = 20.0$. El ángulo $\theta$, entre ellos, es la diferencia: $\theta = \phi - \alpha = 110\degree - 35\degree = 75\degree$. La sustitución de estos valores en la Ecuación 2.27 da el producto escalar.
Solución
Un cálculo directo nos da
$$\bold{\vec{A}}\cdot \bold{\vec{F}}= AFcos\theta = (10.0)(20.0)cos75\degree = 51.76$$ Comprueba tu aprendizaje 2.11
Comprueba tu aprendizaje 2.11
En el sistema de coordenadas cartesianas, los productos escalares del vector unitario de un eje con otros vectores unitarios de otros ejes siempre desaparecen porque son ortogonales:
$$\^{\bold{i}}\cdot \^{\bold{j}} = |\^{\bold{i}}|\cdot|\^{\bold{j}}|cos90\degree = (1)(1)(0) = 0\\ \^{\bold{i}}\cdot \^{\bold{k}} = |\^{\bold{i}}|\cdot|\^{\bold{k}}|cos90\degree = (1)(1)(0) = 0\\ \^{\bold{k}}\cdot \^{\bold{j}} = |\^{\bold{k}}|\cdot|\^{\bold{j}}|cos90\degree = (1)(1)(0) = 0\tag{2.29}$$En estas ecuaciones, usamos el hecho de que las magnitudes de todos los vectores unitarios son uno: $|\^{\bold{i}}| = |\^{\bold{j}}| = |\^{\bold{k}}| = 1$. Para los vectores unitarios de los ejes, la Ecuación 2.28 da las siguientes identidades:
$$\^{\bold{i}}\cdot \^{\bold{i}} = i^2 = \^{\bold{j}}\cdot \^{\bold{j}} = j^2 = \^{\bold{k}}\cdot \^{\bold{k}} = k^2 \tag{2.30}$$El producto escalar $\bold{\vec{A}}\cdot· \bold{\vec{B}}$ también se puede interpretar como el producto de $B$ con la proyección ortogonal $A\perp$ del vector $\bold{\vec{A}}$ en la dirección del vector $\bold{\vec{B}}$ (figura 2.27 (b)) o el producto de $A$ con la proyección ortogonal $B\perp$ del vector $\bold{\vec{B}}$ en la dirección del vector $\bold{\vec{A}}$ (figura 2.27 (c)):
$$\begin{split} \bold{\vec{A}}\cdot \bold{\vec{B}} &= ABcos\phi\\ &= B(Acos\phi) = BA_{\perp}\\ &= A(Bcos\phi) = AB_{\perp} \end{split}$$Por ejemplo, en el sistema de coordenadas rectangulares en un plano, el componente escalar $x$ de un vector es su producto punto con el vector unitario $\^{\bold{i}}$, y el componente escalar $y$ de un vector es su producto punto con el vector unitario $\^{\bold{j}}$:
$$\bold{\vec{A}}\cdot \^{\bold{i}} = |\bold{\vec{A}}||\^{\bold{i}}|cos\theta_A = Acos\theta_A = A_x\\ \bold{\vec{A}}\cdot \^{\bold{j}} = |\bold{\vec{A}}||\^{\bold{j}}|cos(90\degree - \theta)_A = Asen\theta_A = A_y$$La multiplicación escalar de vectores es conmutativa,
$$\bold{\vec{A}}\cdot \bold{\vec{B}} = \bold{\vec{B}}\cdot \bold{\vec{A}}\tag{2.31}$$y obedece a la ley distributiva: $$\bold{\vec{A}}\cdot (\bold{\vec{B}} + \bold{\vec{C}}) = \bold{\vec{A}}\cdot \bold{\vec{B}} + \bold{\vec{A}}\cdot \bold{\vec{C}}$$
(2.32)
Podemos usar las leyes conmutativa y distributiva para derivar varias relaciones para vectores, como expresar el producto punto de dos vectores en términos de sus componentes escalares.
 Comprueba tu aprendizaje 2.12
Comprueba tu aprendizaje 2.12
Cuando los vectores en la Ecuación 2.27 se presentan en sus componentes rectangulares,
$$\bold{\vec{A}} = A_x\^{\bold{i}} + A_y\^{\bold{j}}+ A_z\^{\bold{k}}\\ \bold{\vec{B}} = B_x\^{\bold{i}} + B_y\^{\bold{j}}+ B_z\^{\bold{k}}$$podemos calcular su producto escalar de la siguiente manera:
$$\begin{split} \bold{\vec{A}}\cdot\bold{\vec{B}} &= (A_x\^{\bold{i}} + A_y\^{\bold{j}} + A_z\^{\bold{k}})\cdot(B_x\^{\bold{i}} + B_y\^{\bold{j}} + B_z\^{\bold{k}})\\ &= A_x B_x\bold{i}\cdot\bold{i} + A_x B_y\bold{i}\cdot\bold{j} + A_x B_z\bold{i}\cdot\bold{k}\\ & \;\;\;\;\; + A_y B_x\bold{j}\cdot\bold{i} + A_y B_y\bold{j}\cdot\bold{j} + A_y B_z\bold{j}\cdot\bold{k}\\ & \;\;\;\;\; + A_z B_x\bold{k}\cdot\bold{i} + A_z B_y\bold{k}\cdot\bold{j} + A_z B_z\bold{k}\cdot\bold{k} \end{split}$$Como los productos escalares de dos vectores unitarios de diferentes de ejes dan cero, y los productos escalares de los mismo vectores unitarios dan uno (ver la Ecuación 2.29 y la Ecuación 2.30), solo hay tres términos distintos de cero en la anterior expresión.
Por lo tanto, el producto escalar se simplifica a
Podemos usar la Ecuación 2.33 para el producto escalar en términos de los componentes escalares para encontrar el ángulo entre dos vectores. Cuando dividimos la Ecuación 2.27 por $AB$, obtenemos la ecuación para $cos\phi$, en la cual reemplazamos la Ecuación 2.33:
$$cos\phi = \frac{\bold{\vec{A}}\cdot \bold{\vec{B}}}{AB} = \frac{A_xB_x + A_yB_y + A_zB_z}{AB}\tag{2.34}$$El ángulo $\phi$ entre los vectores $\bold{\vec{A}}$ y $\bold{\vec{B}}$ se obtiene calculando el coseno inverso de la expresión en la Ecuación 2.34.
Ejemplo 2.16
Ángulo entre dos fuerzas
Tres perros están tirando de un palo en diferentes direcciones, como se muestra en la Figura 2.28.
El primer perro tira con fuerza $\bold{\vec{F}}_1 = (10.0\^{\bold{i}} - 20.4\^{\bold{j}} + 2.0\^{\bold{k}}N$, el segundo perro tira con fuerza $\bold{\vec{F}}_2 = (- 15.0\^{\bold{i}} - 6.2\^{\bold{i}})N$, y el tercer perro tira con fuerza $\bold{\vec{F}}_3 = (5.0\^{\bold{i}} + 12.5\^{\bold{j}})N$. ¿Cuál es el ángulo entre las fuerzas $\bold{\vec{F}}_1$ y $\bold{\vec{F}}_2$?
Estrategia
Las componentes del vector de fuerza $\bold{\vec{F}}_1$ son $F_{1x} = 10.0 N, F_{1y} = -20.4N$, y $F_{1z} = 2.0N$, mientras que las del vector de fuerza $\bold{\vec{F}}_2$ son $F_{2x} = - 15.0 N, F_{2y} = 0.0 N$, y $F_{2z} = -6.2N$.
El cálculo del producto escalar de estos vectores y sus magnitudes, y su sustitución en la ecuación 2.34 da el ángulo de interés.

Solución
Las magnitudes de las fuerzas $\bold{\vec{F}}_1$ y $\bold{\vec{F}}_1$ son
$$\begin{split} F_1 &= \sqrt{F_{1x}^2 + F_{1y}^2 + F_{1z}^2}\\ &= \sqrt{10.0^2 + 20.4^2 +2.0^2}N = 22.8N \end{split}$$ y $$\begin{split} F_2 &= \sqrt{F_{2x}^2 + F_{2y}^2 + F_{2z}^2}\\ &= \sqrt{15.0^2 + 6.2^2}N = 16.2N \end{split}$$
La sustitución de los componentes escalares en la ecuación 2.33 da como resultado el producto escalar
$$\begin{split} \bold{\vec{F}}_1\cdot \bold{\vec{F}}_2 &= F_{1x}F_{2x} + F_{1y}F_{2y} + F_{1z}F_{2z}\\ &= (10.0 N)(−15.0 N) + (−20.4 N)(0.0 N)\\ & \;\;\;\;+ (2.0 N)(−6.2 N)\\ &= -162.4N^2 \end{split}$$Finalmente, sustituyendo en la ecuación 2.34 obtenemos el ángulo
$$\begin{split} cos\phi &= \frac{\bold{\vec{F}}_1\cdot \bold{\vec{F}}_2}{F_1F_2}\\ &=\frac{(-162.4)N^2}{(22.8 N)(16.2 N)} = -0.439 \end{split}$$Luego
$$\phi = cos^{-1}(-0.439) = 116.0\degree$$Explicación
Observa que cuando los vectores se dan en términos de los vectores unitarios, podemos encontrar el ángulo entre ellos sin conocer los detalles sobre las direcciones geográficas que representan los vectores unitarios. Aquí, por ejemplo, la dirección $+ x$ podría estar hacia el este y la dirección $+ y$ podría estar hacia el norte.
Pero, el ángulo entre las fuerzas en el problema es el mismo si la dirección $+ x$ está hacia el oeste y la dirección $+ y$ está hacia el sur.
 Comprueba tu aprendizaje 2.13
Comprueba tu aprendizaje 2.13
Ejemplo 2.17
El trabajo de una fuerza
Cuando una fuerza $\bold{\vec{F}}$ tira de un objeto y causa su desplazamiento $\bold{\vec{D}}$, decimos que la fuerza realiza un trabajo.
La cantidad de trabajo que hace la fuerza es el producto escalar $\bold{\vec{F}}\cdot\bold{\vec{D}}$. Si el palo del ejemplo 2.16 se mueve momentáneamente y se desplaza por el vector $\bold{\vec{D}}= (- 7.9\^{\bold{j}} - 4.2\^{\bold{k}})cm$, ¿cuánto trabajo realiza el tercer perro en el ejemplo 2.16 ?
Estrategia
Calculamos el producto escalar del vector de desplazamiento $\bold{\vec{D}}$ con el vector de fuerza $\bold{\vec{F}}_3 = (5.0\^{\bold{i}} + 12.5\^{\bold{j}}) N$, que es la tracción del tercer perro.
Usemos $W_3$ para denotar el trabajo hecho por la fuerza $\bold{\vec{F}}_3$ en el desplazamiento $\bold{\vec{D}}$.
Solución
Calcular el trabajo es una aplicación directa del producto escalar:
Explicación
La unidad de trabajo en el SI se llama joule ($J$), donde $1 J = 1 N\cdot m$. La unidad $cm\cdot N$ se puede escribir como $10^{-2}m\cdot N = 10^{-2}J$, por lo que la respuesta se puede expresar como $W_3 = -0.9875J \approx -1.0J$.
 Comprueba tu aprendizaje 2.14
Comprueba tu aprendizaje 2.14
El producto vectorial de dos vectores (el Producto cruz)
El producto vectorial de dos vectores $\bold{\vec{A}}$ y $\bold{\vec{B}}$ se denota por $\bold{\vec{A}}\times \bold{\vec{B}}$ y a menudo se denomina producto cruz. El producto vectorial es un vector que tiene su dirección perpendicular a ambos vectores $\bold{\vec{A}}$ y $\bold{\vec{B}}$.
En otras palabras, el vector $\bold{\vec{A}}\times \bold{\vec{B}}$ es perpendicular al plano que contiene los vectores $\bold{\vec{A}}$ y &$\bold{\vec{B}}$, como se muestra en la Figura 2.29.
La magnitud del producto vectorial se define como
donde el ángulo $\phi$, entre los dos vectores, se mide del vector $\bold{\vec{A}}$ (primer vector en el producto) al vector $\bold{\vec{B}}$ (segundo vector en el producto), como se indica en la Figura 2.29, y está entre $0\degree$ y $180\degree$. De acuerdo con la Ecuación 2.35, el producto vectorial desaparece para pares de vectores que son paralelos $(\phi = 0\degree)$ o antiparalelos $(\phi = 180\degree)$ porque $sen0\degree = sin180\degree = 0$. (Observa, también, el interactivo para $\phi = 180\degree$).
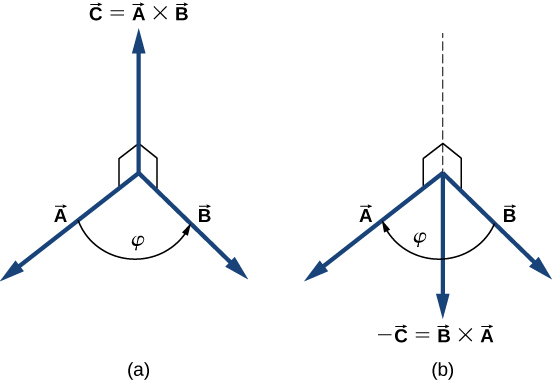
En la línea perpendicular al plano que contiene los vectores $\bold{\vec{A}}$ y $\bold{\vec{B}}$ hay dos direcciones alternativas, arriba o abajo, como se muestra en la Figura 2.29, y la dirección del producto vectorial puede ser cualquiera de ellas. En la orientación estándar a la derecha, donde el ángulo entre vectores se mide en sentido antihorario desde el primer vector, el vector $\bold{\vec{A}}\times \bold{\vec{B}}$ apunta hacia arriba, como se ve en la Figura 2.29 (a). Si invertimos el orden de la multiplicación, de modo que ahora $\bold{\vec{B}}$ es primero en el producto, entonces el vector $\bold{\vec{B}}\times \bold{\vec{A}}$ debe apuntar hacia abajo, como se ve en la Figura 2.29 (b) .
Esto significa que los vectores $\bold{\vec{A}}\times \bold{\vec{B}}$ y $\bold{\vec{B}}\times \bold{\vec{A}}$ son antiparalelos entre sí y que la multiplicación vectorial no es conmutativa, sino anticommutativa. La propiedad anticomutativa significa que el producto vectorial invierte el signo cuando el orden de multiplicación se invierte:
La regla de sacacorchos de la mano derecha es un mnemotécnico utilizado para determinar la dirección del producto vectorial. Como se muestra en la Figura 2.30, se coloca un sacacorchos en una dirección perpendicular al plano que contiene los vectores$\bold{\vec{A}}$ y $\bold{\vec{B}}$, y su mango gira en la dirección del primer vector al segundo vector. La dirección del producto cruz viene dada por la progresión del sacacorchos.
En la escena interactiva anterior, hemos recreado la regla de la mano derecha (sin el sacacorchos).
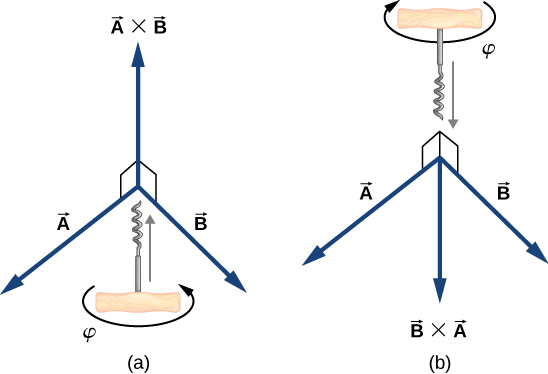
Ejemplo 2.18
El torque de una fuerza
La ventaja mecánica que proporciona una herramienta familiar llamada llave (figura 2.31), depende de la magnitud $F$ de la fuerza aplicada, de su dirección con respecto al mango de la llave, y de cuán lejos de la tuerca se aplica esta fuerza.
La distancia $R$ desde la tuerca hasta el punto donde se une el vector de fuerza $\bold{\vec{F}}$ está representado por el vector radial $\bold{\vec{R}}$. La cantidad de vector físico que hace que la tuerca gire se llama torque o par (denotado por $\bold{\vec{\tau}}$), y es el producto vectorial de la distancia del pivote a la fuerza: $\bold{\vec{\tau}}= \bold{\vec{R}}\times \bold{\vec{F}}$.
Para aflojar una tuerca oxidada, se aplica una fuerza de $20.00 N$ al mango de la llave a un ángulo $\phi = 40\degree$ y a una distancia de $0.25 m$ de la tuerca, como se muestra en la Figura 2.31 (a). Encuentra la magnitud y dirección del torque aplicado a la tuerca. ¿Cuál sería la magnitud y la dirección del torque si la fuerza se aplicara en el ángulo $\phi = 45\degree$, como se muestra en la Figura 2.31 (b)? ¿Para qué valor de ángulo $\phi$ tiene el par la mayor magnitud?
Estrategia
Adoptamos el marco de referencia que se muestra en la figura 2.31, donde los vectores $\bold{\vec{R}}$ y $\bold{\vec{F}}$ se encuentran en el plano $xy$ y el origen está en la posición de la tuerca. La dirección radial a lo largo del vector $\bold{\vec{R}}$ (apuntando desde el origen) es la dirección de referencia para medir el ángulo $\phi$ porque $\bold{\vec{R}}$ es el primer vector en el producto vectorial $\bold{\vec{\tau}} = \bold{\vec{R}}\times \bold{\vec{F}}$. El vector $\bold{\vec{\tau}}$ debe estar a lo largo del eje $z$ porque este es el eje que es perpendicular al plano $xy$, donde están ambos $\bold{\vec{R}}$ y $\bold{\vec{F}}$.
Para calcular la magnitud $\tau$, usamos la Ecuación 2.35. Para encontrar la dirección de $\bold{\vec{\tau}}$, usamos la regla de sacacorchos o de la mano derecha (Figura 2.30).

Solución
Para la situación en (a), la regla del sacacorchos da la dirección de $\bold{\vec{R}}\times \bold{\vec{F}}$ en la dirección positiva del eje $z$. Físicamente, significa que el torque $\bold{\vec{\tau}}$ señala fuera de la página, perpendicular al mango de la llave. Identificamos $F = 20.00 N$ y $R = 0.25 m$, y calculamos la magnitud usando la Ecuación 2.11:
$$\begin{split} T = |\bold{\vec{R}}\times \bold{\vec{F}}| &= RFsen\phi\\ &= (0.25 m)(20.00 N)sen40\degree = 3.21 N\cdot m \end{split}$$Para la situación en (b), la regla del sacacorchos da la dirección de $\bold{\vec{R}}\times \bold{\vec{F}}$ en la dirección negativa del eje $z$. Físicamente, significa que el torque $\bold{\vec{\tau}}$ apunta a la página, perpendicular al mango de la llave. La magnitud de este par es
El torque tiene el mayor valor cuando $sen\phi = 1$, que ocurre cuando $\phi = 90\degree$. Físicamente, significa que la llave inglesa es más efectiva, dándonos la mejor ventaja mecánica, cuando aplicamos la fuerza perpendicular al mango de la llave. Para la situación en este ejemplo, este valor de mejor torque es $$\tau_{\text{óptimo}} = RF = (0.25 m)(20.00N) = 5.00N\cdot m$$
Explicación
Al resolver problemas mecánicos, a menudo no necesitamos usar la regla del sacacorchos o de la mano derecha en absoluto, como veremos ahora en la siguiente solución equivalente. Ten en cuenta que una vez que hemos identificado que el vector $\bold{\vec{R}}\times \bold{\vec{F}}$ se encuentra a lo largo del eje $z$, podemos escribir este vector en términos del vector unitario $\^{\bold{k}}$ del eje $z$:
$$\bold{\vec{R}}\times \bold{\vec{F}} = RF sen\phi \^{\bold{k}}$$En esta ecuación, el número que multiplica $\^{\bold{k}}$ es el componente rectangular $z$ del vector $\bold{\vec{R}}\times \bold{\vec{F}}$. En el cálculo de este componente, se debe tener cuidado en que el ángulo $\phi$ se mida en sentido antihorario desde $\bold{\vec{R}}$ (primer vector) hasta $\bold{\vec{F}}$ (segundo vector).
Siguiendo este principio para los ángulos, obtenemos $RFsen(+40\degree) = + 3.2 N\cdot m$ para la situación en (a), y obtenemos $RFsen(-45\degree) = -3.5 N\cdot m$ para la situación en (b).
En el último caso, el ángulo es negativo porque el gráfico de la Figura 2.31 indica que el ángulo se mide en el sentido de las agujas del reloj; pero, el mismo resultado se obtiene cuando este ángulo se mide en sentido antihorario porque $+ (360\degree - 45\degree) = + 315\degree$ y $sen(+ 315\degree) = sen(-45\degree)$. De esta manera, obtenemos la solución sin referencia a la regla del sacacorchos. Para la situación en (a), la solución es $\bold{\vec{R}}\times \bold{\vec{F}} = +3.2 N\cdot m\^{\bold{k}}$; para la situación en (b), la solución es $\bold{\vec{R}}\times \bold{\vec{F}} = -3.5 N\cdot m\^{\bold{k}}$.
 Comprueba tu aprendizaje 2.15
Comprueba tu aprendizaje 2.15
Similar al producto punto (ecuación 2.32), el producto cruz tiene la siguiente propiedad distributiva
$$\bold{\vec{A}}\times (\bold{\vec{B}} + \bold{\vec{C}}) = \bold{\vec{A}}\times \bold{\vec{B}} + \bold{\vec{A}}\times \bold{\vec{C}}\tag{2.37}$$La propiedad distributiva se aplica con frecuencia cuando los vectores se expresan en sus componentes rectangulares, en términos de los vectores unitarios de los ejes cartesianos.
Cuando aplicamos la definición del producto cruz, ecuación 2.35, a los vectores unitarios $\^{\bold{i}}, \^{\bold{j}}$ y $\^{\bold{k}}$ que definen las direcciones positivas $x, y$, y $z$ en el espacio, encontramos que
$$\^{\bold{i}}\times \^{\bold{i}} = \^{\bold{j}}\times \^{\bold{j}} = \^{\bold{k}}\times \^{\bold{k}} = 0\tag{2.38}$$Todos los demás productos cruz de estos tres vectores unitarios deben ser vectores de magnitudes unitarias, porque $\^{\bold{i}}, \^{\bold{j}}$ y $\^{\bold{k}}$ son ortogonales.
Por ejemplo, para el par $\^{\bold{i}}$ y $\^{\bold{j}}$, la magnitud es $|\^{\bold{i}}\times \^{\bold{j}}| = ijsen90\degree = (1)(1)(1) = 1$. La dirección del producto vectorial $\^{\bold{i}}\times \^{\bold{j}}$ debe ser ortogonal al plano $xy$, lo que significa que debe estar a lo largo del eje $z$. Los únicos vectores unitarios a lo largo del eje $z$ son $-\^{\bold{k}}$ o $+ \^{\bold{k}}$. Por la regla de la mano derecha, la dirección del vector $\^{\bold{i}}\times \^{\bold{j}}$ debe ser paralela al eje $z$ positivo. Por lo tanto, el resultado de la multiplicación $\^{\bold{i}}\times \^{\bold{j}}$ es idéntico a $\^{\bold{k}}$. Podemos repetir un razonamiento similar para los pares restantes de vectores unitarios. Los resultados de estas multiplicaciones son
$$\^{\bold{i}}\times \^{\bold{j}} = \^{\bold{k}}\\ \^{\bold{j}}\times \^{\bold{k}} = \^{\bold{i}}\tag{2.39}\\ \^{\bold{k}}\times \^{\bold{i}} = \^{\bold{j}}$$Observa que en la ecuación 2.39, los tres vectores unitarios $\^{\bold{i}}, \^{\bold{j}}$ y $\^{\bold{k}}$ aparecen en el orden cíclico que se muestra en un diagrama en la figura 2.32(a). El orden cíclico significa que en la fórmula del producto, $\^{\bold{i}}$ sigue a $\^{\bold{k}}$ y está antes de $\^{\bold{j}}$, o $\^{\bold{k}}$ sigue a $\^{\bold{j}}$ y viene antes de $\^{\bold{i}}$ o $\^{\bold{j}}$ sigue a $\^{\bold{i}}$ y viene antes de $\^{\bold{k}}$. El producto cruz de dos vectores unitarios diferentes es siempre un tercer vector unitario. Cuando dos vectores unitarios en el producto cruz aparecen en el orden cíclico, el resultado de dicha multiplicación es el vector unitario restante, como se ilustra en la figura 2.32(b). Cuando los vectores unitarios en el producto cruz aparecen en un orden diferente, el resultado es un vector unitario que es antiparalelo al vector unitario restante, es decir, el resultado es con el signo menos, como se muestra en los ejemplos de la figura 2.32(c) y figura 2.32(d). En la práctica, cuando la tarea es encontrar productos cruz de vectores que se dan en sus componentes vectoriales o rectangulares, esta regla para el producto cruz de vectores unitarios es muy útil.
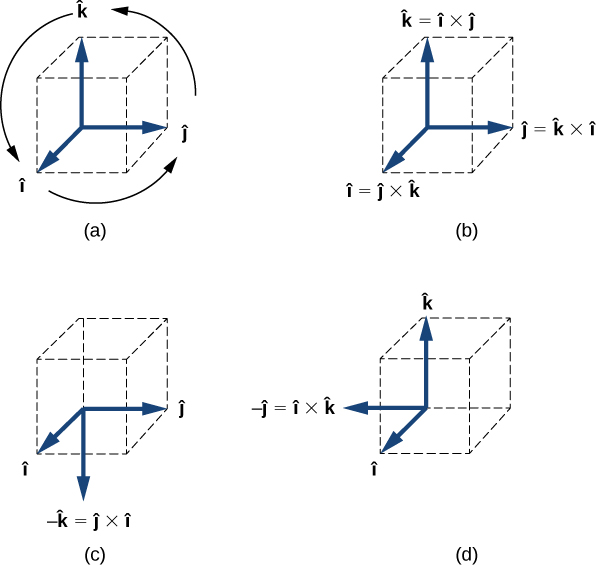
Supongamos que queremos encontrar el producto cruzado $\bold{\vec{A}}\times \bold{\vec{B}}$ para los vectores $\bold{\vec{A}} = A_x\^{\bold{i}} + A_y\^{\bold{j}} + A_z\^{\bold{k}}$ y $\bold{\vec{B}} = B_x\^{\bold{i}} + B_y\^{\bold{j}} + B_z\^{\bold{k}}$. Podemos usar la propiedad distributiva (Ecuación 2.37), la propiedad anticomutativa (Ecuación 2.36) y los resultados en la Ecuación 2.38 y la Ecuación 2.39 para que realizar las siguientes operaciones algebraicas:
Al realizar las operaciones algebraicas que involucren el producto cruz, ten mucho cuidado de mantener el orden correcto de multiplicación porque el producto cruz es anticommutativo. Los dos últimos pasos que todavía tenemos que hacer para completar nuestra tarea son, primero, agrupar los términos que contienen un vector unitario común y, segundo, factorizar.
De esta forma obtenemos la siguiente expresión muy útil para el cálculo del producto cruz:
$$\begin{split} \bold{\vec{C}} &= \bold{\vec{A}}\times \bold{\vec{B}}\\ &= (A_yB_z - A_zB_y)\^{\bold{i}} + (A_zB_x - A_xB_z)\^{\bold{j}}\\ & \;\;\;\;\; + (A_xB_y - A_yB_x)\^{\bold{k}}\tag{2.40} \end{split}$$En esta expresión, los componentes escalares del vector de producto cruz son
$$C_x = A_yB_z - A_zB_y$$Al encontrar el producto cruz, en la práctica, podemos usar la ecuación 2.35 o la ecuación 2.40, dependiendo de cuál de ellas parezca menos compleja desde el punto de vista computacional. Ambos conducen al mismo resultado final. Una forma de asegurarse de que el resultado final sea correcto es usar ambos.
Ejemplo 2.19
Una partícula en un campo magnético
Cuando se mueven, en un campo magnético, algunas partículas pueden experimentar una fuerza magnética. Sin entrar en detalles, un estudio detallado de los fenómenos magnéticos aparece en capítulos posteriores, reconozcamos que el campo magnético $\bold{\vec{B}}$ es un vector, la fuerza magnética $\bold{\vec{F}}$ es un vector, y la velocidad $\bold{\vec{v}}$ de la partícula es un vector.
El vector de fuerza magnética es proporcional al producto vectorial del vector de velocidad con el vector de campo magnético, que expresamos como $\bold{\vec{F}} = \zeta \bold{\vec{u}}\times \bold{\vec{B}}$. En esta ecuación, una constante $\zeta$ se encarga de la consistencia en las unidades físicas, por lo que podemos omitir las unidades físicas en los vectores $\bold{\vec{u}}$ y $\bold{\vec{B}}$. En este ejemplo, supongamos que la constante $\zeta$ es positiva.
Una partícula que se mueve en el espacio con el vector de velocidad $\bold{\vec{u}} = -5.0\^{\bold{i}} - 2.0\^{\bold{j}} + 3.5\^{\bold{k}}$ entra en una región con un campo magnético y experimenta una fuerza magnética.
Encuentra la fuerza magnética $\bold{\vec{F}}$ en esta partícula en el punto de entrada a la región donde está el vector del campo magnético (a) $\bold{\vec{B}} = 7.2\^{\bold{i}} - \^{\bold{j}} - \^{\bold{k}}$ y (b ) $\bold{\vec{B}} = 4.5\^{\bold{k}}$. En cada caso, encuentra la magnitud $F$ de la fuerza magnética y el ángulo $\theta$ del vector de fuerza $\bold{\vec{F}}$ con el vector de campo magnético $\bold{\vec{B}}$.
Estrategia
Primero, queremos encontrar el producto vectorial $\bold{\vec{u}}\times \bold{\vec{B}}$, porque entonces podemos determinar la fuerza magnética usando $\bold{\vec{F}} = \zeta \bold{\vec{u}}\times \bold{\vec{B}}$. La magnitud $F$ se puede encontrar usando componentes,
$$F = \sqrt{F_x^2 + F_y^2 + F_z^2}$$o calculando la magnitud $|\bold{\vec{u}}\times \bold{\vec{B}}|$ directamente, usando la Ecuación 2.35. En este último enfoque, deberíamos encontrar el ángulo entre los vectores $\bold{\vec{u}}$ y $\bold{\vec{B}}$. Cuando tenemos $\bold{\vec{F}}$, el método general para encontrar el ángulo de dirección $\theta$ implica el cálculo del producto escalar $\bold{\vec{u}} \cdot \bold{\vec{B}}$ y la sustitución en la Ecuación 2.34. Para calcular el producto vectorial, podemos usar la ecuación 2.40 o calcular el producto directamente, de la forma que sea más simple.
Solución
Los componentes del vector de velocidad son $u_x = -5.0, u_y = -2.0$, y $u_z = 3.5$.
(a) Las componentes del vector del campo magnético son $B_x = 7.2, B_y = -1.0$, y $B_z = -2.4$. Sustituyéndolos en la Ecuación 2.41 da los componentes escalares del vector $\bold{\vec{F}} = \zeta\bold{\vec{u}}\times \bold{\vec{B}}$:
Por lo tanto, la fuerza magnética es $\bold{\vec{F}} = \zeta(8.3\^{\bold{i}} + 13.2\^{\bold{j}} + 19.4\^{\bold{k}}$ y su magnitud es
$$F = \sqrt{F_x^2 + F_y^2 + F_z^2}\\ F = \zeta\sqrt{8.3)^2 + (13.2)^2 + (19.4)^2} = 24.9\zeta$$Para calcular el ángulo $\theta$, necesitemos encontrar la magnitud del vector de campo magnético,
$$B = \sqrt{B_x^2 + B_y^2 + B_z^2}\\ B = \sqrt{(7.2)^2 + (-1.0)^2 + (-2.4)^2} = 7.6$$y el producto escalar $\bold{\vec{F}} \cdot \bold{\vec{B}}$:
$$\begin{split} \bold{\vec{F}} \cdot \bold{\vec{B}} &= F_xB_x + F_yB_y + F_zB_z\\ &= (8.3\zeta)(7.2) + (13.2\zeta)(−1.0) + (19.4\zeta)(−2.4) = 0 \end{split}$$Ahora, sustituyéndo en la ecuación 2.34 da el ángulo $\theta$:
$$cos\;\theta = \frac{\bold{\vec{F}} \cdot \bold{\vec{B}}}{FB} = \frac{0}{(18.2\zeta)(7.6)} = 0 \implies \theta = 90\degree$$Por lo tanto, el vector de fuerza magnética es perpendicular al vector del campo magnético. (Podríamos haber ahorrado un tiempo si hubiéramos calculado el producto escalar anteriormente).
(b) Como el vector $\bold{\vec{B}} = 4.5\^{\bold{k}}$ tiene solo un componente, podemos realizar el cálculo algebraico rápidamente y encontrar el producto vectorial directamente:
$$\begin{split} \bold{\vec{F}} &= \zeta\bold{\vec{u}} \times \bold{\vec{B}}\\ &= \zeta(-5.0\^{\bold{i}} -2.0\^{\bold{j}} + 3.5\^{\bold{k}})\times (4.5\^{\bold{k}})\\ &= \zeta[(-5.0)(4.5)\^{\bold{i}} \times \^{\bold{k}} + (-2.0)(4.5)\^{\bold{j}} \times \^{\bold{k}} + (3.5)(4.5)\^{\bold{k}} \times \^{\bold{k}}]\\ &= \zeta[-22.5(-\^{\bold{j}}) -9.0(+\^{\bold{i}}) + 0] = \zeta(-9.0\^{\bold{i}} + 22.5\^{\bold{j}}) \end{split}$$La magnitud de la fuerza magnética es $F = \sqrt{F_x^2 + F_y^2 + F_z^2}$
$$F = \zeta\sqrt{(-9.0)^2 + (22.5)^2 + (0.0)^2} = 24.2\zeta$$Porque el producto escalar es
$$\begin{split} \bold{\vec{F}} \cdot \bold{\vec{B}} &= F_xB_x + F_yB_y + F_zB_z\\ &= (−9.0\zeta)(0) + (22.5\zeta)(0) + (0)(4.5) = 0 \end{split}$$el vector de fuerza magnética $\bold{\vec{F}}$ es perpendicular al vector del campo magnético $\bold{\vec{B}}$.
Explicación
Incluso, sin calcular realmente el producto escalar, podemos predecir que el vector de fuerza magnética debe ser siempre perpendicular al vector del campo magnético debido a la forma en que se construye este vector. A saber, el vector de fuerza magnética es el producto vectorial $\bold{\vec{F}} = \zeta\bold{\vec{u}} \times \bold{\vec{B}}$, por la definición del producto vectorial (ver Figura 2.29), el vector $\bold{\vec{F}}$ debe ser perpendicular a ambos vectores $\bold{\vec{u}}$ y $\bold{\vec{B}}$.
 Comprueba tu aprendizaje 2.16
Comprueba tu aprendizaje 2.16
En conclusión a esta sección, queremos enfatizar que el "producto punto" y el "producto cruz" son objetos matemáticos completamente diferentes, que tienen diferentes significados. El producto punto es un escalar; el producto cruz es un vector. Los capítulos posteriores usan los términos producto punto y producto escalar indistintamente. De manera similar, los términos producto cruz o prudcto vectorial se usan indistintamente.
Cinemática: Movimiento
en una línea recta
Galileo Galilei (Pisa, Toscana; 15 de febrero de 1564 -Arcetri, Toscana; 8 de enero de 1642) fue un astrónomo, ingeniero, filósofo, matemático y físico italiano. Entre sus logros se incluye la primera ley del movimiento (imagen de dominio público publicada por Justus Sustermans en https://commons.wikimedia.org/).
Introducción

Nuestro universo está lleno de objetos en movimiento. Desde las estrellas, planetas y galaxias; al movimiento de personas y animales; hasta la escala microscópica de átomos y moléculas: todo en nuestro universo está en movimiento. Podemos describir el movimiento usando las dos disciplinas de cinemática y dinámica. Estudiamos la dinámica, que se ocupa de las causas del movimiento, en las Leyes del movimiento de Newton.
Pero, hay mucho que aprender sobre el movimiento sin referirse a lo que lo causa, y este es el estudio de la cinemática. La cinemática implica describir el movimiento a través de propiedades tales como la posición, el tiempo, la velocidad y la aceleración.
Un tratamiento completo de la cinemática considera el movimiento en dos y tres dimensiones.
Por ahora, discutimos el movimiento en una dimensión, que nos proporciona las herramientas necesarias para estudiar el movimiento multidimensional. Un buen ejemplo de un objeto sometido a movimiento unidimensional es el tren de levitación magnética representado al comienzo de este capítulo. A medida que viajas, digamos, de Tokio a Kioto, te encuentras en diferentes posiciones a lo largo de la ruta en varios momentos de su recorrido y, por lo tanto, tienes desplazamientos o cambios de posición. También tienes una variedad de velocidades a lo largo de tu camino y experimentas aceleraciones (cambios en la velocidad).
Con las habilidades aprendidas en este capítulo, podemos calcular estas cantidades y la velocidad promedio. Todas estas cantidades pueden describirse usando cinemática, sin conocer la masa del tren o las fuerzas involucradas.
Otro ejemplo de movimiento unidimensional lo puedes observar en la siguiente escena interactiva, diseñada por Julio César Domínguez Tovar, publicada en el proyecto Telesecundaria. En este escena se recrea el movimiento de un auto y de otros automotores que viajan a una velocidad mayor. Lo interesante de la simulación es el efecto del sonido en la representación de este movimiento lineal.
Posición, desplazamiento y velocidad promedio
Cuando estás en movimiento, las preguntas básicas son: ¿Dónde estás? ¿A dónde vas? ¿Qué tan rápido estás llegando allí? Las respuestas a estas preguntas requieren que especifiques tu posición, tu desplazamiento y tu velocidad promedio, los términos que definimos en esta sección.
Posición
Para describir el movimiento de un objeto, primero debes describir su posición ($x$): ¿dónde está en un momento determinado? Más precisamente, necesitamos especificar su posición relativa a un marco de referencia conveniente. Un marco de referencia es un conjunto arbitrario de ejes desde el cual se describen la posición y el movimiento de un objeto.
La Tierra se utiliza a menudo como un marco de referencia, y a menudo describimos la posición de un objeto en lo que se refiere a objetos estáticos en la Tierra. Por ejemplo, un lanzacohetes podría describirse como tener una posición del cohete en el mundo. En otros casos, no estamos estáticos sino en movimiento en relación con la Tierra. Para describir la posición de una persona en un avión, por ejemplo, usamos el avión, no la Tierra, como el marco de referencia. Para describir la posición de un objeto que experimenta un movimiento unidimensional, a menudo usamos la variable $x$. Más adelante en el capítulo, durante la discusión sobre la caída libre, usamos la variable $y$.

desplazamiento
Si un objeto se mueve en relación con un marco de referencia, por ejemplo, si un profesor se mueve hacia la derecha en relación con una pizarra (Figura 3.3), entonces la posición del objeto cambia.
Este cambio de posición se llama desplazamiento. La palabra desplazamiento implica que un objeto se ha movido o se ha desplazado. Aunque la posición es el valor numérico de x a lo largo de una línea recta donde se puede ubicar un objeto, el desplazamiento proporciona el cambio de posición a lo largo de esta línea. Como el desplazamiento indica dirección, un vector y puede ser positivo o negativo, dependiendo de la elección de la dirección positiva. Además, un análisis de movimiento puede tener muchos desplazamientos incrustados en él. Si la derecha es positiva y un objeto se mueve $2 m$ hacia la derecha, luego $4 m$ hacia la izquierda, los desplazamientos individuales son $2 m$ y $-4 m$, respectivamente.
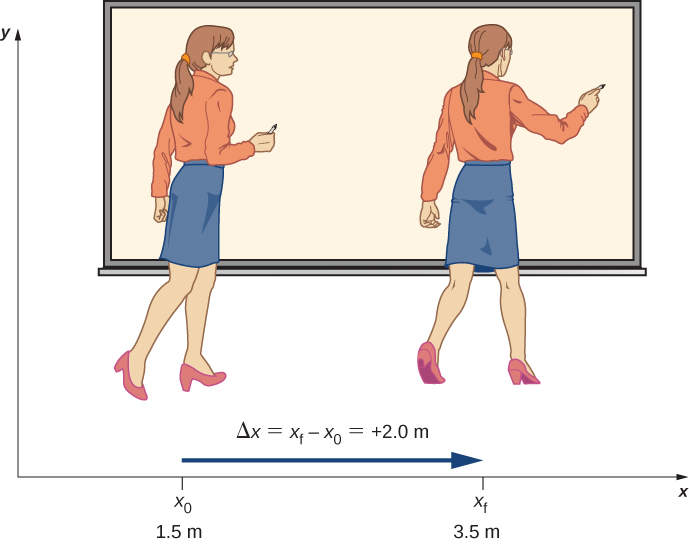
El desplazamiento $\Delta x$ es el cambio en la posición de un objeto:
donde $\Delta x$ es el desplazamiento, $x_f$ es la posición final, y $x_0$ es la posición inicial.
Usamos la letra mayúscula griega delta ($\Delta$) para significar "cambio en" cualquier cantidad que le siga; por lo tanto, $\Delta x$ significa cambio de posición (posición final menos posición inicial). Siempre resolvemos el desplazamiento restando la posición inicial $x_0$ de la posición final $x_f$. Ten en cuenta que la unidad del SI para el desplazamiento es el metro, pero a veces utilizamos kilómetros u otras unidades de longitud. Tenen cuenta, además, que cuando se usan unidades distintas del metro en un problema, es posible que debas convertirlas a metros para completar el cálculo.
Los objetos en movimiento también pueden tener una serie de desplazamientos. En el ejemplo anterior de la profesora, los desplazamientos individuales son de $2 m$ y de $-4m$, lo que da un desplazamiento total de $-2 m$. Definimos el desplazamiento total $\Delta x_\text{Total}$, como la suma de los desplazamientos individuales, y expresamos esto matemáticamente con la ecuación ∑
donde $\Delta x_i$ son los desplazamientos individuales. En el ejemplo anterior,
$Δx_1 = x_1 - x_0 = 2 - 0 = 2m$
Similarmente,
$\Delta x_2 = x_2 - x_1 = -2 - 2 = -4m$
en consecuencia,
$\Delta x_{\text{Total}}= \Delta x_1 + \Delta x_2 = 2 - 4 = -2m$
El desplazamiento total es $2 - 4 = -2 m$ hacia la izquierda, o en la dirección negativa. También es útil para calcular la magnitud del desplazamiento o su tamaño. La magnitud del desplazamiento siempre es positiva. Este es el valor absoluto del desplazamiento, porque el desplazamiento es un vector y no puede tener un valor negativo de magnitud. En nuestro ejemplo, la magnitud del desplazamiento total es de $2 m$, mientras que las magnitudes de los desplazamientos individuales son de $2 m$ y $4m$.
La magnitud del desplazamiento total no debe confundirse con la distancia recorrida. La distancia recorrida $x_{\text{Total}}$, es la longitud total de la ruta recorrida entre dos posiciones. En el problema anterior, la distancia recorrida es la suma de las magnitudes de los desplazamientos individuales:
$$x_{\text{Total}} = |\Delta x_1| + |\Delta x_2| = 2+4 = 6m$$Velocidad media o promedio
Para calcular las otras cantidades físicas en cinemática, debemos introducir la variable tiempo. La variable tiempo nos permite, no solo indicar dónde está el objeto (su posición) durante su movimiento, sino también qué tan rápido se mueve.
La velocidad a la que se mueve un objeto está dada por la velocidad a la que la posición cambia con el tiempo. Para cada posición $x_i$, asignamos un tiempo particular $t_i$. Si los detalles del movimiento en cada instante no son importantes, la velocidad generalmente se expresa como la velocidad promedio $\={v}$. Esta cantidad vectorial es simplemente el desplazamiento total entre dos puntos dividido por el tiempo necesario para viajar entre ellos. El tiempo necesario para viajar entre dos puntos se denomina tiempo transcurrido $\Delta t$.
Si $x_1$ y $x_2$ son las posiciones de un objeto en los momentos $t_1$ y $t_2$, respectivamente, entonces
$$\begin{split} \text{Velocidad promedio } &= \={v}\\ &= \frac{\text{Desplazamiento entre los dos puntos}}{\text{Tiempo transcurrido entre los dos puntos}} \end{split}$$
Es importante notar que la velocidad promedio es un vector y puede ser negativa, dependiendo de las posiciones $x_1$ y $x_2$.
Ejemplo 3.1
Entrega de folletos
Juanita sale de su casa para repartir volantes para su venta de garaje, viajando hacia el este a lo largo de su calle llena de casas.
A $0.5 km$ y $9$ minutos más tarde se queda sin volantes y tiene que volver sobre sus pasos de regreso a su casa para obtener más. Esto demora otros $9$ minutos. Después de recoger más volantes, se pone de nuevo en el mismo camino, continúa donde lo dejó y termina a $1,0 km$ de su casa. Esta tercera etapa de su viaje lleva $15$ minutos. En este punto, vuelve a su casa, dirigiéndose al oeste. Después de $1.75 km$ y $25$ minutos, ella se detiene para descansar.
- ¿Cuál es el desplazamiento total de Juanita hasta el punto donde ella se detiene para descansar?
- ¿Cuál es la magnitud del desplazamiento final?
- ¿Cuál es la velocidad promedio durante todo su viaje?
- ¿Cuál es la distancia total recorrida?
- Haz un gráfico de posición versus tiempo.
Un esquema de los movimientos de Juanita se muestra en la Figura 3.4.
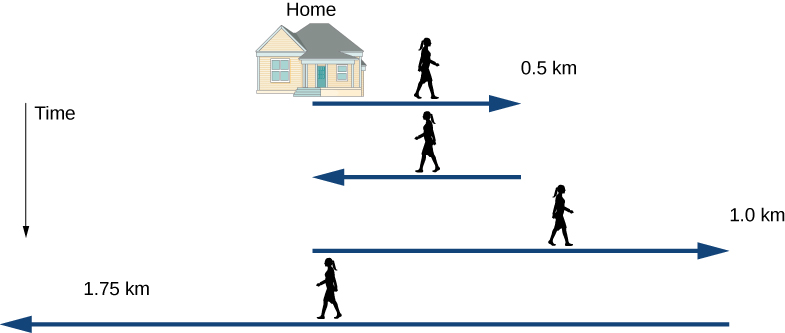
Estrategia
El problema contiene datos sobre las distintas etapas del viaje de Juanita, por lo que sería útil hacer una tabla de las cantidades físicas. Se nos da una posición y tiempo en la redacción del problema para que podamos calcular los desplazamientos y el tiempo transcurrido. Tomamos hacia el este como la dirección positiva. A partir de esta información, podemos encontrar el desplazamiento total y la velocidad promedio. El hogar de Juanita es el punto de partida $x_0$. La siguiente tabla muestra el tiempo y la posición de Juanita en las dos primeras columnas, y los desplazamientos se calculan en la tercera columna.
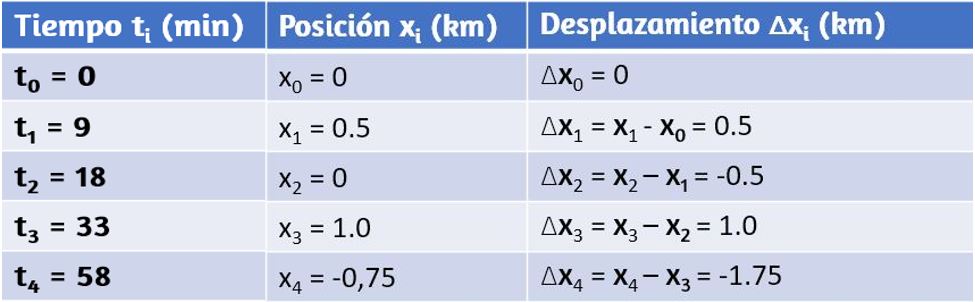
Solución
- De la tabla anterior, el desplazamiento total es $\sum\Delta x_i = 0.5 −0.5 + 1.0 − 1.75 km = −0.75 km$
- La magnitud del desplazamiento total es $|-0.75| km = 0.75 km$.
- Velocidad promedio = $\={v} = \frac{-0.75km}{58min} = -0.013km/min$
- Podemos graficar la posición de Juanita contra el tiempo como una ayuda útil para ver el movimiento; el gráfico se muestra en la Figura 3.5
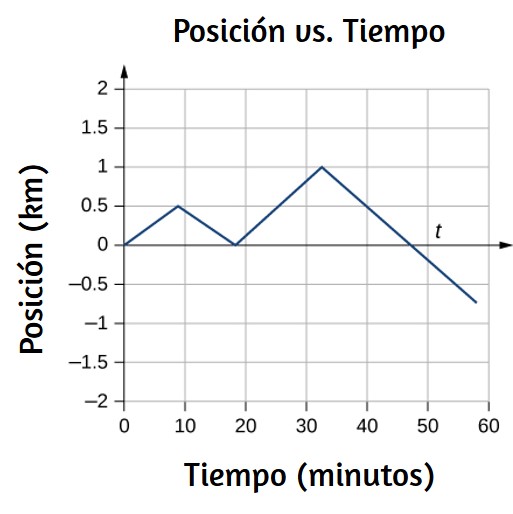
Explicación
El desplazamiento total de Juanita es de $-0.75 km$, lo que significa que al final de su viaje termina a $0.75 km$. al oeste de su casa.
La velocidad promedio significa que si alguien caminara hacia el oeste a $0.013 km/min$ comenzando al mismo tiempo que Juanita salía de su casa, ambos llegarían al último punto de parada al mismo tiempo. Ten en cuenta que si Juanita terminara su viaje en su casa, su desplazamiento total sería cero, así como su velocidad promedio. La distancia total recorrida durante los $58$ minutos de tiempo transcurrido para su viaje es de $3.75 km$.
En la siguiente escena interactiva, diseñada por Juan Guillermo Rivera Berrío, puedes observar los movimientos de Juanita
 Comprueba tu aprendizaje 3.1
Comprueba tu aprendizaje 3.1

Velocidad instantánea y Rapidez
Ahora hemos visto cómo calcular la velocidad promedio entre dos posiciones. Sin embargo, dado que los objetos en el mundo real se mueven continuamente a través del espacio y el tiempo, nos gustaría encontrar la velocidad de un objeto en cualquier punto. Podemos encontrar la velocidad del objeto en cualquier punto de su camino mediante el uso de algunos principios fundamentales del cálculo. Esta sección nos brinda una mejor comprensión de la física del movimiento y será útil en capítulos posteriores.
Velocidad instantánea
La cantidad física que nos dice qué tan rápido se mueve un objeto a lo largo de su camino es la velocidad instantánea, generalmente llamada simplemente velocidad.
Es la velocidad promedio entre dos puntos definida como el límite del tiempo (y, por lo tanto, el desplazamiento) entre los dos puntos se aproxima a cero. Para ilustrar esta idea matemáticamente, necesitamos expresar la posición $x$ como una función continua de $t$ denotada por $x(t)$. La expresión de la velocidad promedio entre dos puntos usando esta notación es $\={v} = \frac{x(t_2) - x(t_1)}{t_2-t_1}$. Para encontrar la velocidad instantánea en cualquier posición, hacemos $t_1 = t$ y $t_2 = t + \Delta t$. Después de insertar estas expresiones en la ecuación para la velocidad promedio y tomar el límite como $\Delta t \to 0$, encontramos la expresión para la velocidad instantánea:
$$v(t) = \lim\limits_{\Delta t \to 0} \frac{x(t+\Delta t) - x(t)}{\Delta t} = \frac{dx(t)}{dt}$$La velocidad instantánea de un objeto es el límite de la velocidad promedio cuando el tiempo transcurrido se acerca a cero, o la derivada de $x$ con respecto a $t$ es:
Al igual que la velocidad promedio, la velocidad instantánea es un vector con dimensión de longitud por tiempo. La velocidad instantánea en un punto de tiempo específico $t_0$ es la tasa de cambio de la función de posición, que es la pendiente de la función de posición $x(t)$ en $t_0$. La Figura 3.6 muestra cómo la velocidad promedio $\={v} = \frac{\Delta x}{\Delta t}$ entre dos tiempos que se aproximan a la velocidad instantánea en $t_0$.
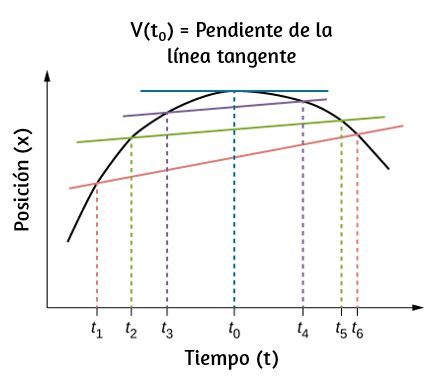
La velocidad instantánea se muestra en el tiempo $t_0$, que está en el máximo de la función de posición.
La pendiente del gráfico de posición es cero en este punto, y por lo tanto la velocidad instantánea es cero. En otros momentos, $t_1, t_2$, y así sucesivamente, la velocidad instantánea no es cero porque la pendiente del gráfico de posición sería positiva o negativa. Si la función de posición tuviera un mínimo, la pendiente del gráfico de posición también sería cero, dando una velocidad instantánea de cero allí también. Por lo tanto, los ceros de la función de velocidad dan el mínimo y el máximo de la función de posición.
Ejemplo 3.2
Encontrar la velocidad desde un gráfico de posición versus tiempo
Dado el gráfico de posición versus tiempo de la Figura 3.7, encuentra el gráfico de velocidad versus tiempo.
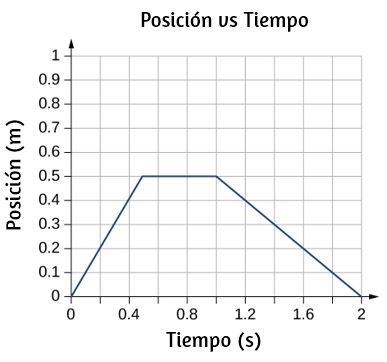
Estrategia
El gráfico contiene tres líneas rectas en tres intervalos de tiempo. Hallamos la velocidad en cada intervalo de tiempo tomando la pendiente desde la cuadrícula.
Solución
Intervalo de $0$ a $0.5$ s: $\displaystyle\={v} = \frac{\Delta x}{\Delta t} = \frac{0.5m - 0.0m}{0.5s - 0.0s} = 1.0m/s$
Intervalo de $0.5$ a $1.0$ s: $\displaystyle\={v} = \frac{\Delta x}{\Delta t} = \frac{0.0m - 0.0m}{1.0s - 0.5s} = 0.0m/s$
Intervalo de $1.0$ a $2.0$ s: $\displaystyle\={v} = \frac{\Delta x}{\Delta t} = \frac{0.0m - 0.5m}{2.0s - 1.0s} = -0.5m/s$
El gráfico de estos valores de velocidad versus tiempo se muestra en la Figura 3.8.
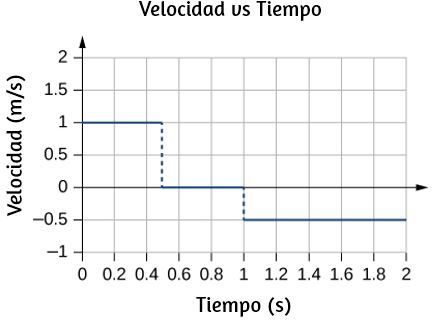
Explicación
Durante el intervalo de tiempo entre $0.0 s$ y $0.5 s$, la posición del objeto se aleja del origen y la curva de posición versus tiempo tiene una pendiente positiva. En cualquier punto a lo largo de la curva durante este intervalo de tiempo, podemos encontrar la velocidad instantánea tomando su pendiente, que es $+1 m/s$, como se muestra en la Figura 3.8. En el siguiente intervalo de tiempo, entre $0.5 s$ y $1.0 s$, la posición no cambia y vemos que la pendiente es cero. De $1.0$ a $2.0 s$, el objeto se está moviendo hacia atrás hacia el origen y la pendiente es de $-0.5 m/s$. El objeto tiene una dirección invertida y tiene una velocidad negativa.
Rapidez
En el lenguaje cotidiano, la mayoría de las personas usa los términos rapidez y velocidad de manera intercambiable. En física, sin embargo, no tienen el mismo significado y son conceptos distintos. Una gran diferencia es que la rapidez no tiene ninguna dirección; es decir, la rapidez es un escalar.
Podemos calcular la rapidez promedio encontrando la distancia total recorrida dividida por el tiempo transcurrido:
La rapidez promedio no es necesariamente la misma que la magnitud de la velocidad promedio, que se encuentra al dividir la magnitud del desplazamiento total por el tiempo transcurrido.
Por ejemplo, si un viaje comienza y termina en la misma ubicación, el desplazamiento total es cero y, por lo tanto, la velocidad promedio es cero. La rapidez promedio, sin embargo, no es cero, porque la distancia total recorrida es mayor que cero. Si tomamos un viaje por carretera de $300 km$ y necesitamos estar en nuestro destino en un momento determinado, entonces estaríamos interesados en nuestra rapidez promedio.
Sin embargo, podemos calcular la rapidez instantánea a partir de la magnitud de la velocidad instantánea:
Si una partícula se mueve a lo largo del eje $x$ a $+7.0 m/s$ y otra partícula se mueve a lo largo del mismo eje a $-7.0 m/s$, tienen diferentes velocidades, pero ambas tienen la misma rapidez de $7.0 m/s$. Algunas velocidades típicas se muestran en la Tabla 3.1.
Cálculando de velocidad instantánea
Al calcular la velocidad instantánea, necesitamos especificar la forma explícita de la función de posición $x(t)$. Por el momento, usemos polinomios $x(t) = At^n$, porque se diferencian fácilmente usando la regla de potencia del cálculo:
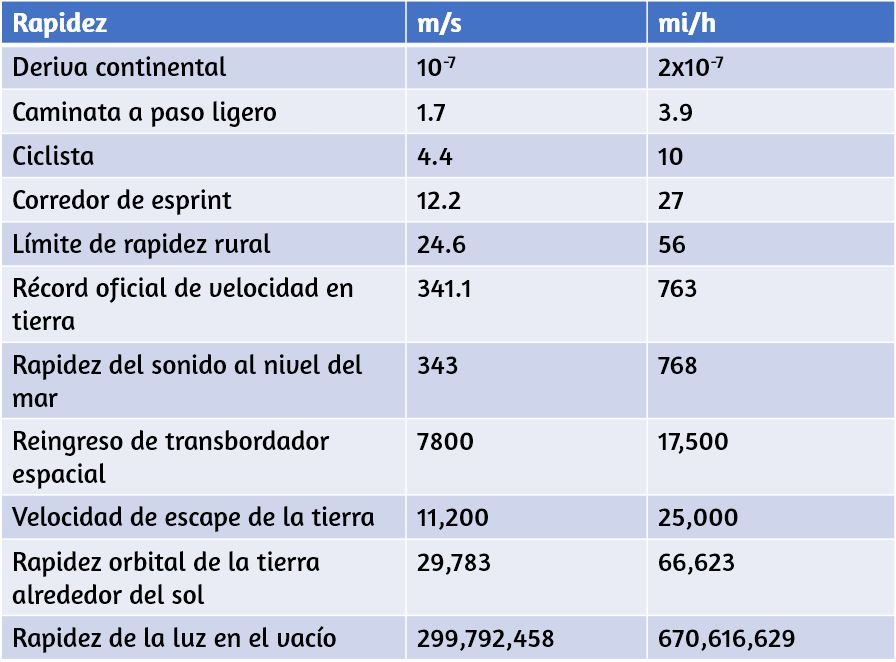
El siguiente ejemplo ilustra el uso de la Ecuación anterior.
Ejemplo 3.3
Velocidad instantánea versus velocidad promedio
La posición de una partícula está dada por $x(t) = 3.0t + 0.5t^3 m.$
- Usando la ecuaciones 3.4 y 3.7, encuentra la velocidad instantánea en $t = 2.0 s$.
- Calcula la velocidad promedio entre $1.0 s$ y $3.0 s$.
Estrategia
La ecuación 3.4 da la velocidad instantánea de la partícula como la derivada de la función de posición. Al observar la forma de la función de posición dada, vemos que es un polinomio en $t$. Por lo tanto, podemos usar la ecuación 3.7, la regla de las potencias del cálculo, para encontrar la solución. Usamos la ecuación 3.6 para calcular la velocidad promedio de la partícula.
Solución
- $v(t) = \frac{dx(t)}{dt} = 3.0 + 1.5t^2 m/s$
- Sustituyendo $t = 2.0 s$ en esta ecuación, obtenemos $v(2.0s) = [3.0 + 1.5(2.0)^2] m/s = 9.0 m/s$.
Para determinar la velocidad promedio de la partícula entre $1.0 s$ y $3.0 s$, calculamos los valores de $x(1.0 s)$ y $x(3.0 s)$: $$x(1.0s) = [(3.0)(1.0) + 0.5(1.0)^3]m = 3.5m\\ x(3.0s) = [(3.0)(3.0) + 0.5(3.0)^3]m = 22.5m\\ \={v} = \frac{x(3.0s) - x(1.0s)}{t(3.0s) - t(1.0s)} = \frac{22.5 - 3.5 m}{3.0 - 1.0 s} = 9.8 m/s$$
Explicación
En el límite en que el intervalo de tiempo utilizado para calcular $\={v}$ se pone en cero, el valor obtenido para $\={v}$ converge al valor de $v$.
Ejemplo 3.4
Velocidad instantánea versus rapidez
Considera el movimiento de una partícula en la que la posición es $x(t) = 3.0t - 3t^2 m$.
- ¿Cuál es la velocidad instantánea en $t = 0.25 s, t = 0.50 s$, y $t = 1.0 s$?
- ¿Cuál es la rapidez de la partícula en estos valores de $t$?
Estrategia
La velocidad instantánea es la derivada de la función de posición y la rapidez es la magnitud de la velocidad instantánea. Usamos las Ecuaciónes 3.4 y 3.7 para resolver la velocidad instantánea.
Solución
- $v(t) = \frac{dx(t)}{dt} = 3.0 -6.0t m/s$
- $v(0.25s) = 1.50 m/s, v(0.5s) = 0 m/s, v(1.0s) = - 3.0 m/s$
- $\text{Rapidez} = |v(t)| = 1.50 m/s, 0.0 m/s$, y $3.0 m/s$
Explicación
La velocidad de la partícula nos da información de su dirección, lo que indica que la partícula se mueve a la izquierda (oeste) o derecha (este). La rapidez da la magnitud de la velocidad. Graficando la posición, la velocidad y la rapidez como funciones del tiempo, podemos entender estos conceptos visualmente.
En la Figura 3.9, en (a), el gráfico muestra que la partícula se mueve en la dirección positiva hasta $t = 0.5 s$, cuando invierte la dirección. La inversión de dirección también puede verse en (b) a $0.5 s$ donde la velocidad es cero y luego se vuelve negativa. A los $1.0 s$ vuelve al origen donde comenzó. La velocidad de la partícula en $1.0 s$ en (b) es negativa, porque viaja en la dirección negativa. Pero en (c), sin embargo, su rapidez es positiva y permanece positiva durante todo el tiempo de viaje. También podemos interpretar la velocidad como la pendiente del gráfico de posición versus tiempo. La pendiente de x(t) está disminuyendo hacia cero, volviéndose cero a $0.5 s$ y cada vez más negativa a partir de ese momento. Este análisis de comparar los gráficos de posición, velocidad y rapidez, ayuda a detectar errores en los cálculos. Los gráficos deben ser consistentes entre sí y ayudar a interpretar los cálculos.
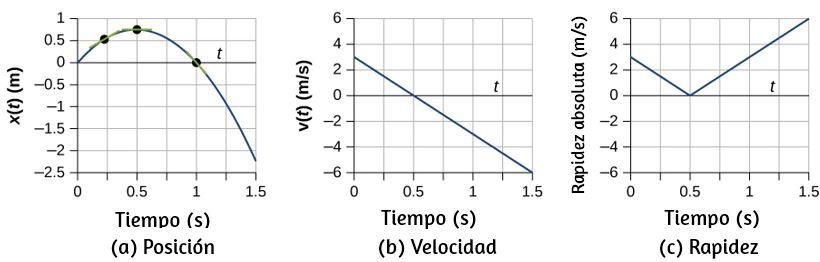
 Comprueba tu aprendizaje 3.2
Comprueba tu aprendizaje 3.2
Aceleración promedio e instantánea
La importancia de comprender la aceleración abarca nuestra experiencia cotidiana, así como los vastos alcances del espacio exterior y el pequeño mundo de la física subatómica. En la conversación cotidiana, acelerar significa aumentar la velocidad; aplicar el pedal de freno hace que el vehículo disminuya la velocidad. Estamos familiarizados con la aceleración de nuestro automóvil, por ejemplo. Cuanto mayor es la aceleración, mayor es el cambio en la velocidad en un tiempo dado.
La aceleración se ve ampliamente en la física experimental. En experimentos del acelerador lineal de partículas, por ejemplo, las partículas subatómicas se aceleran a velocidades muy altas en experimentos de colisión, que nos informan sobre la estructura del mundo subatómico y el origen del universo. En el espacio, los rayos cósmicos son partículas subatómicas que se han acelerado a energías muy altas en las supernovas (explosiones de estrellas masivas) y núcleos galácticos activos.
Es importante comprender los procesos que aceleran los rayos cósmicos porque estos rayos contienen una radiación altamente penetrante que puede dañar la electrónica en una nave espacial, por ejemplo.
Aceleración promedio
La definición formal de aceleración es consistente con estas nociones que acabamos de describir, pero es más inclusiva. La aceleración promedio es la velocidad a la que cambia la velocidad:
donde $\={a}$ es la aceleración promedio, $v$ es la velocidad y $t$ es el tiempo (La barra sobre la letra $a$ significa promedio).
Como la aceleración es velocidad en metros dividida por el tiempo en segundos, las unidades en el SI para la aceleración a menudo se abrevian $m/s^2$, es decir, metros por segundo al cuadrado o metros por segundo por segundo. Esto literalmente significa cuántos metros por segundo la velocidad cambia cada segundo. Recuerda que la velocidad es un vector, tiene tanto magnitud como dirección, lo que significa que un cambio en la velocidad puede ser un cambio en la magnitud (o rapidez), pero también puede ser un cambio en la dirección. Por ejemplo, si un corredor que viaja a $10 km/h$ hacia el este se ralentiza hasta detenerse, luego invierte la dirección, continúa su carrera a 1$0 km/h$ hacia el oeste, su velocidad ha cambiado como resultado del cambio de dirección, aunque la magnitud de la velocidad es la misma en ambas direcciones. Por lo tanto, la aceleración se produce cuando la velocidad cambia en magnitud (un aumento o disminución de la velocidad) o en la dirección, o en ambas.
En la siguiente escena interactiva, diseñada por Carlos Alberto Jaimes Vergara, inicia con una velocidad del auto en $2.5 m/s$ y aceleración cero.
Luego de unos segundos detén el coche y aumenta la aceleración a $2.5 m/s^2$, unos segundos más paras el auto y reduce la aceleración a $2.5 m/s^2$. Observa los resultados en la gráfica. Puedes practicar con otras situaciones.
Aceleración como un vector
La aceleración es un vector en la misma dirección que el cambio en la velocidad, $\Delta v$. Como la velocidad es un vector, puede cambiar en magnitud o en dirección, o ambas cosas. La aceleración es, por lo tanto, un cambio en la velocidad o dirección, o ambas.
Ten en cuenta que, aunque la aceleración está en la dirección del cambio de velocidad, no siempre se produce en la dirección del movimiento. Cuando un objeto se ralentiza, su aceleración es opuesta a la dirección de su movimiento. Aunque esto se conoce comúnmente como desaceleración, en la figura 3.10, decimos que el tren está acelerando en una dirección opuesta a su dirección de movimiento.

El término desaceleración puede causar confusión en nuestro análisis porque no es un vector y no apunta a una dirección específica con respecto a un sistema de coordenadas, por lo que no lo usamos. La aceleración es un vector, por lo que debemos elegir el signo apropiado para ello en nuestro sistema de coordenadas elegido. En el caso del tren de la figura 3.10, la aceleración es en la dirección negativa en el sistema de coordenadas elegido, por lo que decimos que el tren está experimentando una aceleración negativa.
Si un objeto en movimiento tiene una velocidad en la dirección positiva con respecto a un origen elegido y adquiere una aceleración negativa constante, el objeto eventualmente se detiene y revierte la dirección. Si esperamos lo suficiente, el objeto pasa por el origen yendo en la dirección opuesta. Esto se ilustra en la figura 3.11.
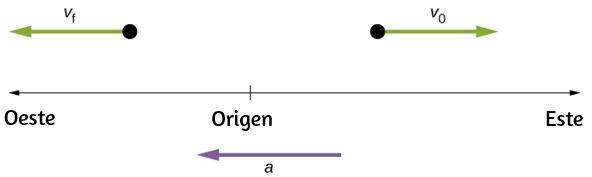
Ejemplo 3.5
Calculando la aceleración promedio: un caballo de carreras deja la puerta
Un caballo de carreras, que sale de la puerta, acelera desde el reposo a una velocidad de $15.0 m/s$ hacia el oeste en $1.80 s$. ¿Cuál es su aceleración promedio?
Estrategia
Primero dibujamos un boceto y asignamos un sistema de coordenadas al problema (figura 3.13). Este es un problema simple, pero siempre ayuda a visualizarlo. Observa que asignamos el Este como positivo y el Oeste como negativo. Por lo tanto, en este caso, tenemos una velocidad negativa.

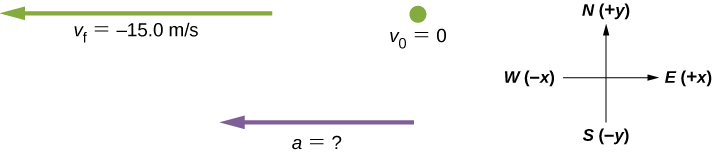
Podemos resolver este problema identificando $\Delta v$ y $\Delta t$ a partir de la información dada, y luego calculando la aceleración promedio directamente desde la ecuación
$$\={a} = \frac{\Delta v}{\Delta t} = \frac{v_f-v_0}{t_f-t_0}$$Solución
Primero, identifica los datos dados: $v_0 = 0, v_f = -15.0 m/s$ (el signo negativo indica dirección hacia el oeste), $\Delta t = 1.80 s$.
Segundo, encuentra el cambio en la velocidad. Como el caballo va de cero a $-15.0 m/s$, su cambio de velocidad es igual a su velocidad final: $\Delta v = v_f - v_0 = v_f = -15.0 m/s$.
Por último, sustituye los valores conocidos ($\Delta v$ y $\Delta t$) y halla $\={a}$:
$$\={a} = \frac{\Delta v}{\Delta t} = \frac{-15.0m/s}{1.8s} = -8.33 m/s^2$$Explicación
El signo negativo de aceleración indica que la aceleración es hacia el oeste. Una aceleración de $8.33 m/s^2$ hacia el oeste significa que el caballo aumenta su velocidad en $8.33 m/s$ hacia el oeste cada segundo; es decir, $8.33 $metros por segundo por segundo, que escribimos como $8.33 m/s^2$. Esta es realmente una aceleración promedio, porque el viaje no es suave. Vemos más adelante que una aceleración de esta magnitud requeriría que el caballo aguante con una fuerza casi igual a su peso.
 Comprueba tu aprendizaje 3.3
Comprueba tu aprendizaje 3.3
Aceleración instantánea
La aceleración instantánea $a$, o la aceleración en un instante específico en el tiempo, se obtiene usando el mismo proceso discutido para la velocidad instantánea. Es decir, calculamos la velocidad promedio entre dos puntos en el tiempo separados por $\Delta t$, dejando que $\Delta t$ se acerque a cero. El resultado es la derivada de la función de velocidad $v(t)$, que es la aceleración instantánea y se expresa matemáticamente como
Por lo tanto, similar a la velocidad que es la derivada de la función de posición, la aceleración instantánea es la derivada de la función de velocidad. Podemos mostrar esto gráficamente de la misma manera que la velocidad instantánea.
En la figura 3.14, la aceleración instantánea en el tiempo $t_0$ es la pendiente de la línea tangente al gráfico de velocidad versus tiempo en el tiempo $t_0$. Vemos que la aceleración promedio $\={a} = \frac{\Delta v}{\Delta t}$ se acerca a la aceleración instantánea cuando $\Delta t$ se aproxima a cero. También en la parte (a) de la figura, vemos que la velocidad tiene un máximo cuando su pendiente es cero. Este tiempo corresponde al cero de la función de aceleración. En la parte (b), se muestra la aceleración instantánea a la velocidad mínima, que también es cero, ya que la pendiente, en ese punto de la curva, también es cero.
Por lo tanto, para una función de velocidad dada, los ceros de la función de aceleración dan la velocidad mínima o la máxima.
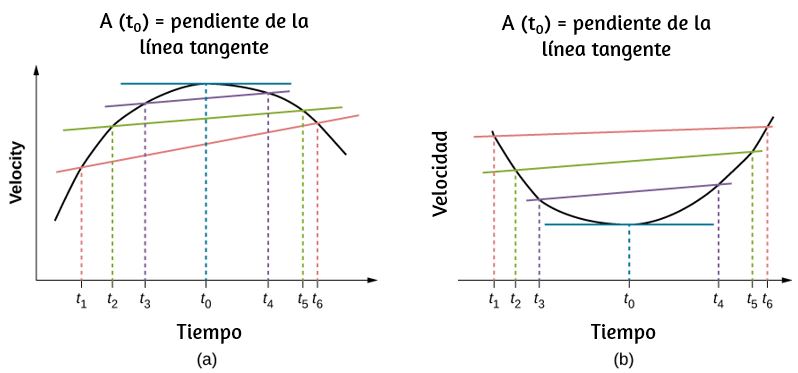
Para ilustrar este concepto, veamos dos ejemplos. Primero, se muestra un ejemplo simple usando la figura 3.9(b), el gráfico de velocidad versus tiempo del Ejemplo 3.3, para encontrar la aceleración gráficamente. Este gráfico se representa en la figura figura 3.15(a), que es una línea recta. El gráfico correspondiente de aceleración versus tiempo se encuentra desde la pendiente de la velocidad y se muestra en la figura figura 3.15(b).
En este ejemplo, la función de velocidad es una línea recta con pendiente constante, por lo que la aceleración es una constante. En el siguiente ejemplo, la función de velocidad tiene una dependencia funcional más complicada del tiempo.
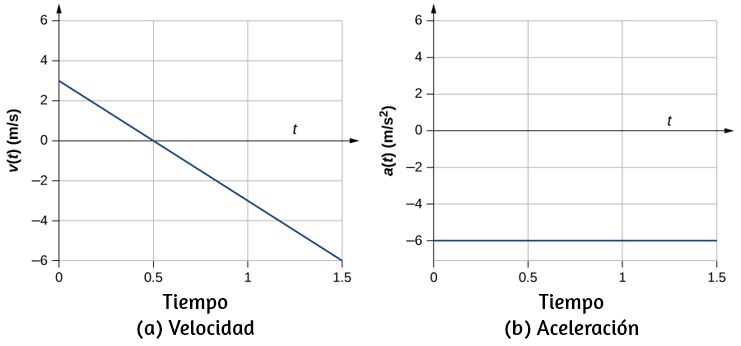
Si conocemos la forma funcional de la velocidad, $v(t)$, podemos calcular la aceleración instantánea $a(t)$ en cualquier punto del tiempo en el movimiento usando la Ecuación 3.9.
Ejemplo 3.6
Calculando aceleración instantánea
Una partícula está en movimiento y se está acelerando. La función de la velocidad es $v(t) = 20t - 5t^2 m/s$.
- Encuentra la forma funcional de la aceleración.
- Encuentra la velocidad instantánea en $t = 1, 2, 3 y 5 s$.
- Encuentra la aceleración instantánea en $t = 1, 2, 3 y 5 s$.
- Interpreta los resultados de (c) en términos de las direcciones de los vectores de aceleración y velocidad.
Estrategia
Encontramos la forma funcional de la aceleración tomando la derivada de la función de velocidad. Luego, calculamos los valores de velocidad instantánea y aceleración a partir de las funciones dadas para cada t dado. Para la parte (d), necesitamos comparar las direcciones de velocidad y aceleración en cada momento.
Solución
- $a(t) = \frac{dv(t)}{dt} = 20 - 10t m/s^2$
- $v(1s) = 15 m/s, v(2s) = 20 m/s, v(3s) = 15m/s, v(5s) = −25m/s$
- $a(1s) = 10 m/s^2, a(2s) = 0 m/s^2, \\a(3s) = −10 m/s^2, a(5s) =− 30 m/s^2$
- En $t = 1 s$, la velocidad $v(1s) = 15 m/s$ es positiva y la aceleración es positiva, por lo tanto, la velocidad y la aceleración están en la misma dirección. La partícula se está moviendo más rápido.
En $t = 2 s$, la velocidad ha aumentado a $v(2s) = 20 m/s$, donde es máxima, que corresponde al tiempo en que la aceleración es cero. Vemos que la velocidad máxima ocurre cuando la pendiente de la función de velocidad es cero, que es el cero de la función de aceleración.
En $t = 3 s$, la velocidad es $v(3s) = 15 m/s$ y la aceleración es negativa. La partícula ha reducido su velocidad y el vector de aceleración es negativo. La partícula se está desacelerando.
En $t = 5 s$, la velocidad es $v(5s) = - 25 m/s$ y la aceleración es cada vez más negativa. Entre los tiempos $t = 3 s$ y $t = 5 s$, la partícula ha reducido su velocidad a cero y luego se vuelve negativa, invirtiendo así su dirección. La partícula ahora está acelerando nuevamente, pero en la dirección opuesta.
Podemos ver estos resultados gráficamente en la figura 3.16.
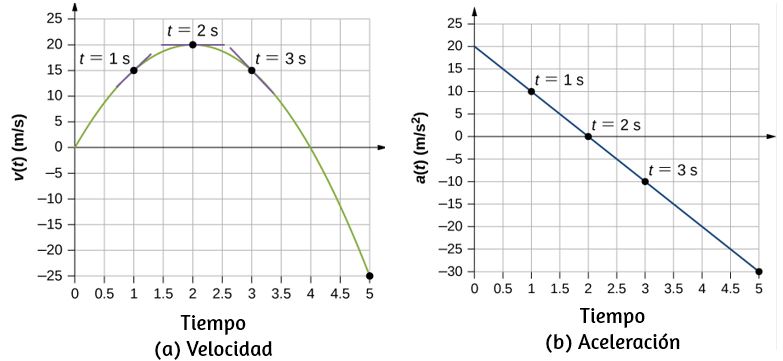
Explicación
Al hacer un análisis numérico y gráfico de la velocidad y la aceleración de la partícula, podemos aprender mucho sobre su movimiento. El análisis numérico complementa el análisis gráfico al brindar una vista total del movimiento. El cero de la función de aceleración corresponde al máximo de la velocidad en este ejemplo.
También en este ejemplo, cuando la aceleración es positiva y en la misma dirección que la velocidad, la velocidad aumenta. A medida que la aceleración tiende a cero, llegando a ser negativa, la velocidad alcanza un máximo, después de lo cual comienza a disminuir. Si esperamos lo suficiente, la velocidad también se vuelve negativa, lo que indica una inversión de dirección. Un ejemplo real de este tipo de movimiento es un automóvil con una velocidad que aumenta hasta un máximo, después de lo cual comienza a disminuir, se detiene y luego invierte la dirección.
 Comprueba tu aprendizaje 3.4
Comprueba tu aprendizaje 3.4
Obteniendo una sensación de aceleración
Probablemente estés acostumbrado a experimentar aceleración cuando entras en un ascensor, o pisas el pedal del acelerador en tu automóvil. Sin embargo, la aceleración está sucediendo en muchos otros objetos en nuestro universo con los que no tenemos contacto directo. La tabla 3.2 presenta la aceleración de varios objetos. Podemos ver que las magnitudes de las aceleraciones se extienden en muchos órdenes de magnitud.
En esta tabla, vemos que las aceleraciones típicas varían ampliamente con diferentes objetos y no tienen nada que ver con el tamaño del objeto ni con su tamaño. La aceleración también puede variar ampliamente con el tiempo durante el movimiento de un objeto. Un drag racer tiene una gran aceleración justo después de su inicio, pero luego disminuye a medida que el vehículo alcanza una velocidad constante.
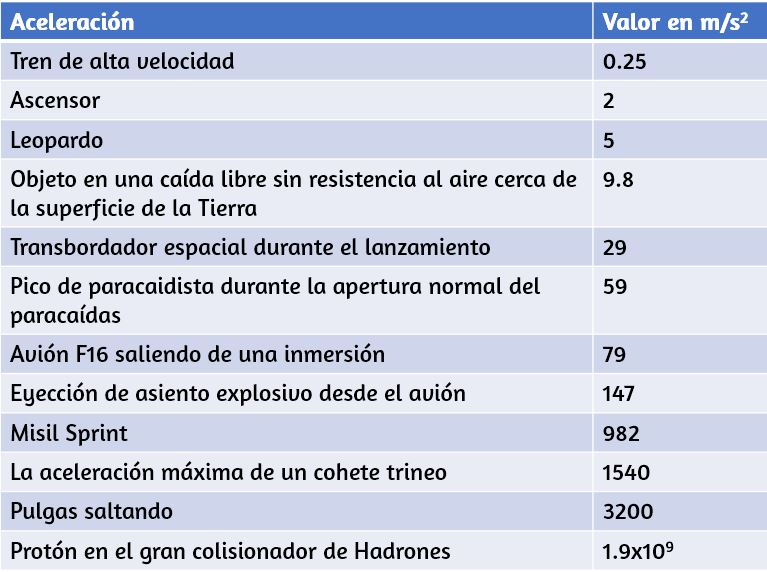
Su aceleración promedio puede ser bastante diferente de su aceleración instantánea en un momento particular durante su movimiento. La figura 3.17 compara la aceleración gráfica promedio con la aceleración instantánea para dos movimientos muy diferentes.
Movimiento uniformemente acelerado
Puedes adivinar que cuanto mayor es la aceleración de, por ejemplo, un automóvil que se aleja de una señal de pare, mayor es el desplazamiento del automóvil en un momento dado. Pero, no hemos desarrollado una ecuación específica que relacione la aceleración y el desplazamiento.
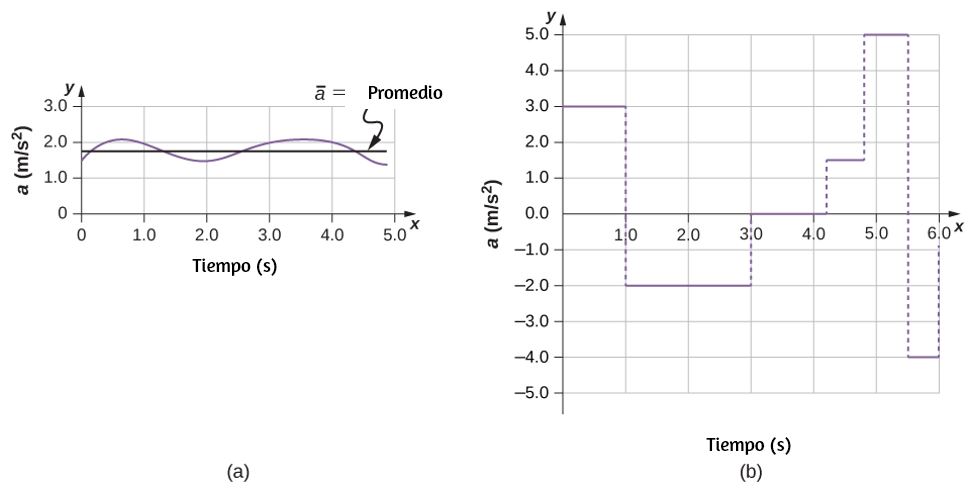
En esta sección, observamos algunas ecuaciones convenientes para relaciones cinemáticas, comenzando a partir de las definiciones de desplazamiento, velocidad y aceleración. Primero investigamos un solo objeto en movimiento, llamado movimiento de un cuerpo. Luego investigamos el movimiento de dos objetos, llamados problemas de persecución o de encuentro de dos cuerpos.
Notación
Primero, hagamos algunas simplificaciones en notación. Hacemos el tiempo inicial cero, como si el tiempo se midiera con un cronómetro, es una gran simplificación.
Como el tiempo transcurrido es $\Delta t = t_f - t_0$, tomar $t_0 = 0$ significa que $\Delta t = t_f$, el tiempo final en el cronómetro. Cuando el tiempo inicial se toma como cero, usamos el subíndice $0$ para denotar los valores iniciales de posición y velocidad. Es decir, $x_0$ es la posición inicial y $v_0$ es la velocidad inicial. No usamos subíndices en los valores finales. Es decir, $t$ es el tiempo final, $x$ es la posición final y $v$ es la velocidad final. Esto da una expresión más simple para el tiempo transcurrido, $\Delta t = t$. También simplifica la expresión para el desplazamiento $x$, que ahora es $\Delta x = x - x_0$. Además, simplifica la expresión de cambio en la velocidad, que ahora es $\Delta v = v - v_0$. Para resumir, usando la notación simplificada, con el tiempo inicial tomado como cero,
$$\Delta t = t\\ \Delta x = x-x_0\\ \Delta v = v-c_0$$donde el subíndice $0$ denota un valor inicial y la ausencia de un subíndice denota un valor final en cualquier movimiento que se esté considerando.
Ahora hacemos la importante suposición de que la aceleración es constante. Esta suposición nos permite evitar el uso de cálculo para encontrar la aceleración instantánea. Como la aceleración es constante, las aceleraciones promedio e instantáneas son iguales, es decir,
$$\={a} = a = \text{constante}$$Por lo tanto, podemos utilizar el símbolo $a$ para la aceleración en todo momento. Asumir que la aceleración sea constante no limita seriamente las situaciones que podemos estudiar ni degrada la precisión de nuestro tratamiento.
Por un lado, la aceleración es constante en una gran cantidad de situaciones. Además, en muchas otras situaciones podemos describir el movimiento con precisión suponiendo una aceleración constante igual a la aceleración promedio de ese movimiento. Por último, para el movimiento durante el cual la aceleración cambia drásticamente, como un automóvil que acelera a la velocidad máxima y luego frena hasta detenerse, el movimiento se puede considerar en partes separadas, cada una de las cuales tiene su propia aceleración constante.
Desplazamiento y posición desde la velocidad
Para obtener nuestras dos primeras ecuaciones, comenzamos con la definición de velocidad promedio:
$$\={v} = \frac{\Delta x}{\Delta t}$$sustituyendo la notación simplificada por $\Delta x$ y $\Delta t$, obtenemos
$$\={v} = \frac{x-x_0}{t}$$Resolviendo para x nos da
donde la velocidad promedio es
La ecuación $\={v} = \frac{v_0+v}{2}$ refleja el hecho que cuando la aceleración es constante, $v$ es simplemente el promedio de las velocidades inicial y final. La Figura 3.18 ilustra este concepto gráficamente. En la parte (a) de la figura, la aceleración es constante, y la velocidad aumenta a una velocidad constante. La velocidad promedio durante el intervalo de 1 h desde $40 km/h$ hasta $80 km/h$ es de $60 km/h$:
$$\={v} = \frac{v_0+v}{2} = \frac{40 km/h}{80 km/h} = 60 km/h$$En la parte (b), la aceleración no es constante. Durante el intervalo de 1 h, la velocidad es más cercana a $80 km/h$ que a $40 km/h$. Por lo tanto, la velocidad promedio es mayor que en la parte (a).
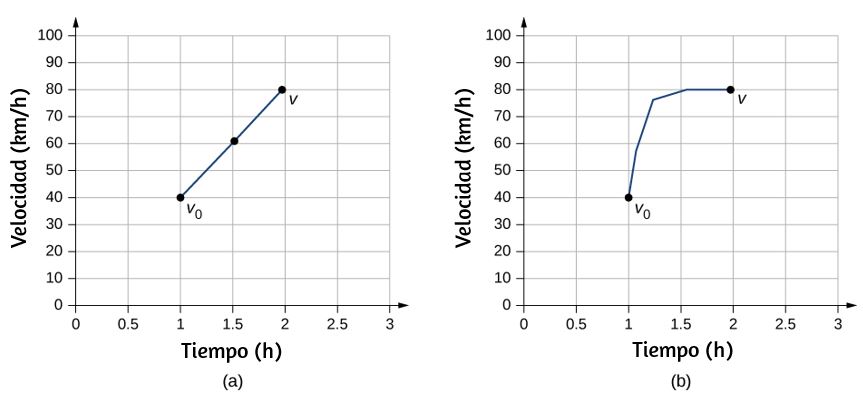
Hallando la velocidad final desde la aceleración y el tiempo
Podemos derivar otra ecuación útil desde la definición de aceleración: $a = \frac{\Delta v}{\Delta t}$
Al sustituir la notación simplificada para $\Delta v$ y $\Delta t$ nos da
Ejemplo 3.7
Cálculo de velocidad final
Un avión aterriza con una velocidad inicial de $70.0 m/s$ y luego desacelera a $1.50 m/s^2$ durante $40.0 s$. ¿Cuál es su velocidad final?
Estrategia
Primero, identificamos los datos conocidos:
$v_0 = 70 m/s, a = -1,50 m/s^2, t = 40 s$.
Segundo, identificamos el dato desconocido; en este caso, es la velocidad final $v_f$.
Por último, determinamos qué ecuación usar. Para hacer esto, averiguamos qué ecuación cinemática da lo desconocido en términos de los datos conocidos. Calculamos la velocidad final usando la Ecuación 3.12, $v = v_0 + at$.
Solución
Sustituye los valores conocidos y resuelve:
$v = v_0 + at = 70.0m/s + (−1.50m/s^2)(40.0 s) = 10.0 m/s$
La Figura 3.19 es un esquema, que muestra los vectores de aceleración y velocidad.

Explicación
La velocidad final es mucho menor que la velocidad inicial, como se desea cuando se ralentiza, pero sigue siendo positiva (ver figura). Con los motores a reacción, el empuje inverso se puede mantener el tiempo suficiente para detener el avión y comenzar a moverlo hacia atrás, lo que se indica mediante una velocidad final negativa, pero no es el caso aquí.
Además de ser útil en la resolución de problemas, la ecuación $v = v_0 + at$ nos da una idea de las relaciones entre la velocidad, la aceleración y el tiempo. Podemos ver, por ejemplo, que
- La velocidad final depende de qué tan grande es la aceleración y cuánto dura
- Si la aceleración es cero, entonces la velocidad final es igual a la velocidad inicial ($v = v_0$), como se esperaba (en otras palabras, la velocidad es constante)
- Si a es negativa, entonces la velocidad final es menor que la velocidad inicial
Todas estas observaciones se ajustan a nuestra intuición. Ten en cuenta que siempre es útil examinar las ecuaciones básicas a la luz de nuestra intuición y experiencia para comprobar que de hecho describen la naturaleza con precisión.
Hallando la posición final con aceleración constante
Podemos combinar las ecuaciones anteriores para encontrar una tercera ecuación que nos permita calcular la posición final de un objeto que experimenta una aceleración constante. Comenzamos con $v = v_0 + at$
Al sumar $v_0$ a cada lado de esta ecuación y dividir por $2$ nos da
$$\frac{v_0+v}{2} = v_0+\frac12 t$$Dado que $\frac{v_0+v}{2}=\={v}$ para la aceleración constante, tenemos
$$\={v}= v_0+\frac12 at$$Sustituimos esta expresión en la ecuación $x = x_0 + \={v}t$, obteniendo
Ejemplo 3.8
Cálculo del desplazamiento de un objeto acelerado
El Dragsters puede lograr una aceleración promedio de $26.0 m/s^2$. Supongamos que un dragster acelera desde el reposo a esta velocidad durante $5,56 s$. (figura 3.20). ¿Qué tan lejos viaja en este momento?

Estrategia
Primero, dibujemos un esquema (figura 3.21).
Se nos pide que descubramos el desplazamiento, que es $x$ si tomamos $x_0$ igual a cero. (Piensa en $x_0$ como la línea de inicio de una carrera. Puede estar en cualquier parte, pero la llamamos cero y mide todas las otras posiciones relativas a ella.) Podemos usar la ecuación $x = x_0 + v_0t + \frac12 at^2$ cuando identifiquemos $v_0, a$, y $t$ en la descripción del problema.
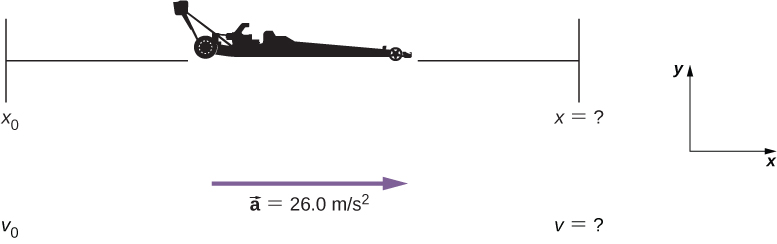
Solución
Primero, necesitamos identificar los datos conocidos. Comenzar desde el reposo significa que $v_0 = 0$, la aceleración $a$ se da como $26.0 m/s^2$ y $t$ es $5.56 s$. En segundo lugar, sustituimos los valores conocidos en la ecuación para hallar el dato desconocido:
$$x = x_0 + v_0t + \frac12 at^2$$Como la posición inicial y la velocidad son ambas cero, esta ecuación se simplifica a
$$x=\frac12 at^2$$sustituyendo los valores de a y t, obtenemos
$$x=\frac12 (26.0 m/s^2)(5.56s)^2 = 402m$$Explicación
Si convertimos $402 m$ a millas, encontramos que la distancia recorrida es muy cercana a un cuarto de milla, la distancia estándar para carreras de resistencia. Entonces, nuestra respuesta es razonable. Este es un desplazamiento impresionante para cubrir en solo $5.56 s$, pero los dragsters de primera categoría pueden recorrer un cuarto de milla en incluso menos tiempo que éste. Si al dragster se le diera una velocidad inicial, esto agregaría otro término a la ecuación de distancia. Si se usan la misma aceleración y el mismo tiempo en la ecuación, la distancia recorrida sería mucho mayor.
¿Qué más podemos aprender al examinar la ecuación $x = \frac12 at^2$? Podemos ver las siguientes relaciones:
- El desplazamiento depende del cuadrado del tiempo transcurrido cuando la aceleración no es cero. En el Ejemplo 3.8, el dragster cubre solo un cuarto de la distancia total en la primera mitad del tiempo transcurrido.
- Si la aceleración es cero, entonces la velocidad inicial es igual a la velocidad promedio ($v_0 = \={v}$ ), y $x = x_0 + v_0t + \frac12 at^2$ se convierte en $x = x_0 + v_0 t$.
Hallando la velocidad final a partir de la distancia y la aceleración
Una cuarta ecuación útil puede obtenerse de otra manipulación algebraica de ecuaciones previas. Si resolvemos $v = v_0 + at$ para $t$, obtenemos
Sustituyendo esta ecuación y $\={v} = \frac{v+v_0}{2}$ en $x = x_0 + \={v}t$, obtenemos
Ejemplo 3.9
Cálculo de la velocidad final
Calcula la velocidad final del dragster en el ejemplo 3.8 sin usar información sobre el tiempo.
Estrategia
La ecuación $v^2 = v_0^2 + 2a(x - x_0)$ es ideal para esta tarea porque relaciona velocidades, aceleración y desplazamiento, y no se requiere información de tiempo.
Solución
Primero, identificamos los datos conocidos. Sabemos que $v_0 = 0$, ya que el dragster comienza desde el reposo. También sabemos que $x - x_0 = 402 m$ (esta fue la respuesta en el Ejemplo 3.8). La aceleración promedio fue dada por $a = 26.0 m/s^2$.
En segundo lugar, sustituimos los datos en la ecuación
$v^2 = v_0^2 + 2a(x - x_0)$ y hallamos $v$:
Luego,
$$v^2 = 2.09\times 10^4 m^2/s^2\\ v = \sqrt{2.09\times 10^4 m^2/s^2} = 145m/2$$Explicación
Una velocidad de $145 m/s$ es de aproximadamente $522 km/h$, o aproximadamente $324 mi/h$, pero incluso esta velocidad vertiginosa es inferior al récord del cuarto de milla. Además, ten en cuenta que una raíz cuadrada tiene dos valores; tomamos el valor positivo para indicar una velocidad en la misma dirección que la aceleración.
Un examen de la ecuación $v^2 = v_0^2 + 2a(x - x_0)$ puede producir información adicional sobre las relaciones generales entre las cantidades físicas:
- La velocidad final depende de cuán grande es la aceleración y la distancia sobre la que actúa.
- Para una aceleración fija, un automóvil que va dos veces más rápido no se detiene en el doble de distancia. Se necesita mucho más para detenerse. (Es por eso que hemos reducido las zonas de velocidad cerca de las escuelas).
Poniendo la ecuaciones juntas
En los siguientes ejemplos, continuamos explorando el movimiento unidimensional, pero en situaciones que requieren un poco más de manipulación algebraica. Los ejemplos también dan una idea de las técnicas de resolución de problemas. La nota que sigue se proporciona para una fácil referencia a las ecuaciones necesarias. Ten en cuenta que estas ecuaciones no son independientes.
En muchas situaciones, tenemos dos incógnitas y necesitamos dos ecuaciones de este conjunto para resolver las incógnitas. Necesitamos tantas ecuaciones como incógnitas para resolver una situación dada.
$$x = x_0 + \={v}t\\ \={v} =\frac{v_0+v}{2}\\ v = v_0 a+t\\ x = x_0 + v_0t +\frac12 at^2\\ v^2=v_0^2 +2a(x-x_0)$$Antes de entrar en los ejemplos, veamos algunas de las ecuaciones más de cerca para ver el comportamiento de la aceleración en valores extremos. Reordenando la ecuación 3.12, tenemos
$$a = \frac{v - v_0}{t}$$De esto vemos que, durante un tiempo finito, si la diferencia entre las velocidades inicial y final es pequeña, la aceleración es pequeña, acercándose a cero en el límite, de tal forma que las velocidades inicial y final son iguales. Por el contrario, en el límite $t \to 0$ para una diferencia finita entre las velocidades inicial y final, la aceleración se vuelve infinita.
Del mismo modo, reorganizando la Ecuación 3.14, podemos expresar la aceleración en términos de velocidades y el desplazamiento:
$$a = \frac{v^2 - v_0^2}{2(x-x_0)}$$Por lo tanto, para una diferencia finita entre las velocidades inicial y final, la aceleración se vuelve infinita en el límite, el desplazamiento se acerca a cero.
La aceleración se acerca a cero en el límite, la diferencia en las velocidades inicial y final se aproxima a cero para un desplazamiento finito.
Antes de presentar más ejemplos, observa la siguiente escena interactiva, diseñada por Inmaculada Sevila Pascual, del proyecto EDAD, publicado por la Red Descartes.
Ejemplo 3.10
¿Hasta dónde va un automóvil?
En un piso de concreto seco, un automóvil puede desacelerar a una velocidad de $7.00 m/s^2$, mientras que en hormigón húmedo puede desacelerar a tan solo $5.00 m/s^2$. Encuentra las distancias necesarias para detener un automóvil que se mueve a $30.0 m/s$ (aproximadamente $110 km/h$) en (a) concreto seco y (b) concreto húmedo. (c) Repite ambos cálculos y encuentra el desplazamiento desde el punto donde el conductor ve un semáforo en rojo, teniendo en cuenta que su tiempo de reacción es de $0.500 s$ para poner su pie en el freno.
Estrategia
Primero, necesitamos dibujar un esquema (figura 3.22). Para determinar qué ecuaciones son las mejores para usar, tenemos que enumerar todos los valores conocidos e identificar exactamente qué tenemos que resolver.
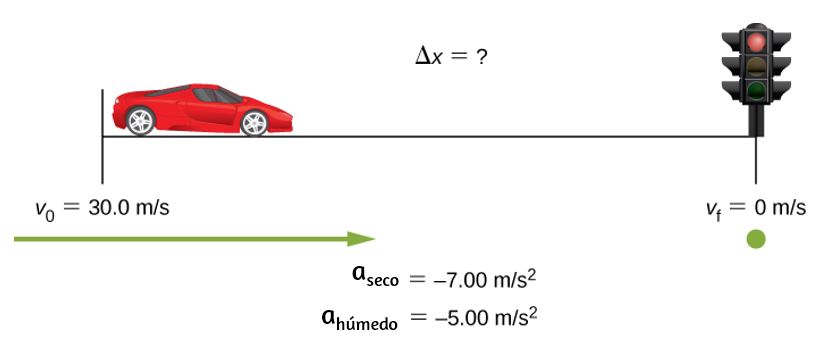
Solución
a. Primero, necesitamos identificar los datos conocidos y lo que queremos resolver. Sabemos que $v_0 = 30.0 m/s $ y $a = -7.00 m/s^2$ ($a$ es negativo porque está en una dirección opuesta a la velocidad). Tomamos $x^2$ igual a cero. Estamos buscando el desplazamiento $\Delta x$, o $(x - x_0)$.
En segundo lugar, identificamos la ecuación que nos ayudará a resolver el problema. La mejor ecuación para usar es
$$v^2 = v_0^2 + 2a(x - x_0)$$Esta ecuación es mejor porque incluye solo una variable desconocida, $x$. Conocemos los valores de todas las otras variables en esta ecuación. (Otras ecuaciones nos permitirían resolver para $x,$ pero requieren que sepamos el tiempo de parada, t, que no conocemos. Podríamos usarlas, pero conllevaría cálculos adicionales).
En tercer lugar, reorganizamos la ecuación para resolver x
$$x - x_0 = \frac{v^2 - v_0^2}{2a}$$sustituyendo los valores conocidos:
$$x - 0 = \frac{0^2 - (30.0 m/s)^2}{2(-7.00 m/s^2)}$$Entonces,
$$x = 64.3 m \text{ en concreto seco}$$b. Esta parte se puede resolver exactamente de la misma manera que (a). La única diferencia es que la aceleración es $-5.00 m/s^2$. El resultado es
$x = 90.0 m$ en concreto mojado.
c. Cuando el conductor reacciona, la distancia de parada es la misma que en (a) y (b) para concreto seco y húmedo. Entonces, para responder a esta pregunta, debemos calcular qué tan lejos viaja el automóvil durante el tiempo de reacción, y luego agregar ese dato al tiempo de parada. Es razonable suponer que la velocidad permanece constante durante el tiempo de reacción del conductor.
Para hacer esto, nuevamente, identificamos los datos conocidos y lo que queremos resolver. Sabemos que $\={v} = 30.0 m/s, t_{\text{reacción}} = 0.500 s$, y $a_{\text{reacción}} = 0$. Consideramos que $x_{\text{0 - reacción}}$ es cero. Estamos buscando $x_{\text{reacción}}$.
$$x = 0 + (30.0 m/s)(0.500 s) = 15.0 m.$$Esto significa que el automóvil viaja $15.0 m$ mientras el conductor reacciona, haciendo que los desplazamientos totales en los dos casos de concreto seco y húmedo sean 15.0 m mayores que si reaccionara instantáneamente.
Por último, sumamos el desplazamiento durante el tiempo de reacción al desplazamiento al frenar (figura 3.23),
$$x_{\text{frenado}} + x_{\text{reacción}} = c_{\text{total}}$$Encontrando que (a) es $64.3 m + 15.0 m = 79.3 m$ cuando está seco y (b) que es $90.0 m + 15.0 m = 105 m$ cuando está húmedo.
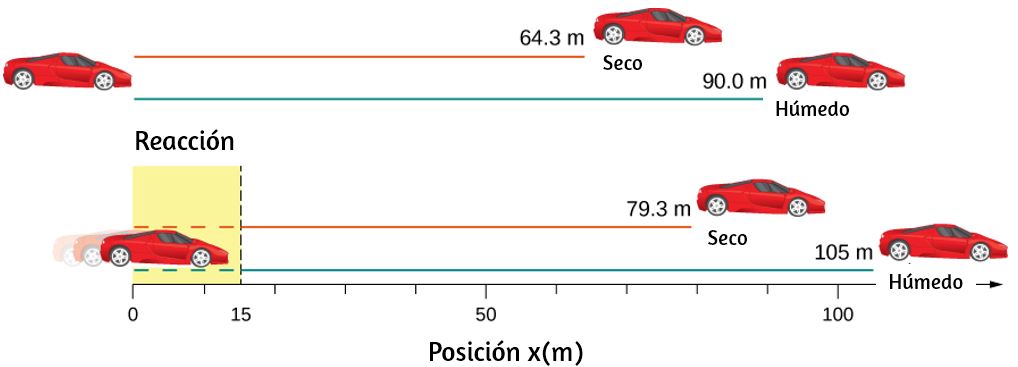
Explicación
Los desplazamientos encontrados en este ejemplo parecen razonables para detener un automóvil que se mueve rápidamente. Debería llevar más tiempo detener un automóvil en el pavimento mojado que en el seco. Es interesante que el tiempo de reacción se agrega significativamente a los desplazamientos, pero más importante es el enfoque general para resolver problemas. Identificamos los datos dados y las cantidades que se determinarán, luego buscamos una ecuación apropiada. Si hay más de un dato desconocido, necesitamos tantas ecuaciones independientes como incógnitas para resolver.
A menudo hay más de una forma de resolver un problema. Las diversas partes de este ejemplo pueden, de hecho, ser resueltas por otros métodos, pero las soluciones presentadas aquí son las más cortas.
Ejemplo 3.11
Calculando el tiempo
Supongamos que un automóvil se une al tráfico de la autopista en una rampa de $200 m$ de longitud. Si su velocidad inicial es $10.0 m/s$ y acelera a $2.00 m/s^2$, ¿cuánto tiempo le lleva al automóvil recorrer los 200 m por la rampa? (Tal información puede ser útil para un ingeniero de tráfico).
Estrategia
Primero, dibujamos un esquema (figura 3.24). Se nos pide que solucionemos el tiempo t. Como antes, identificamos las cantidades conocidas para elegir una relación física conveniente (es decir, una ecuación con una variable desconocida, $t$).
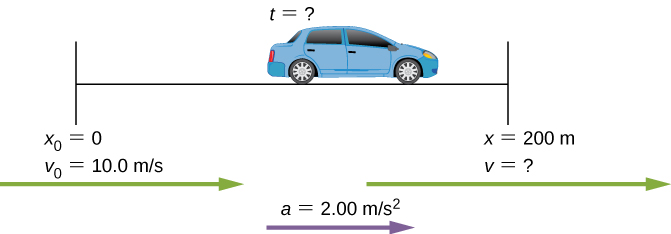
Solución
De nuevo, identificamos los datos conocidos y lo que queremos resolver. Sabemos que $x_0 = 0, v_0 = 10 m/s, a = 2.00 m/s^2$ y $x = 200 m$.
Necesitamos hallar $t$. La ecuación $x = x_0 + v_0t + \frac12 at^2$ funciona mejor porque el único dato desconocido en la ecuación es la variable $t$. Desde esta perspectiva, vemos que cuando ingresamos los datos conocidos en la ecuación, terminamos con una ecuación cuadrática. Necesitamos reorganizar la ecuación para hallar $t$, luego sustituir los datos en la ecuación:
$$200 m = 0 m + (10.0 m/s)t + \frac12 (2.00 m/s^2)t^2$$Entonces, simplificamos la ecuación. Las unidades de metros se cancelan porque están en cada término. Podemos obtener las unidades de segundos para cancelar tomando $t = t s$, donde $t$ es la magnitud del tiempo y $s$ es la unidad. Haciendo esto obtenemos
$$200 = 10t + t^2$$Luego usamos la fórmula cuadrática para hallar $t$,
$$t^2 + 10t -200 = 0\\ t = \frac{-b\pm \sqrt{b^2-4ac}}{2a}$$que produce dos soluciones: $t = 10.0$ y $t = -20.0$. Un valor negativo para el tiempo no es razonable, ya que significaría que el evento sucedió $20 s$ antes de que comenzara el movimiento. Podemos descartar esa solución. Así,
$$t = 10.0 s$$Explicación
Siempre que una ecuación contenga una incognita al cuadrado, hay dos soluciones.
En algunos problemas, ambas soluciones son significativas; en otros, solo una solución es razonable. La respuesta de $10.0 s$ parece razonable para una entrada típica en la autopista.
 Comprueba tu aprendizaje 3.5
Comprueba tu aprendizaje 3.5
Ejemplo 3.12
Aceleración de una nave espacial
Una nave espacial ha abandonado la órbita de la Tierra y está camino hacia la Luna. Se acelera a $20 m/s^2$ durante $2 min$ y cubre una distancia de $1000 km$. ¿Cuáles son las velocidades inicial y final de la nave espacial?
Estrategia
Se nos pide que encontremos las velocidades inicial y final de la nave espacial. Al observar las ecuaciones cinemáticas, vemos que una ecuación no dará la respuesta. Debemos usar una ecuación cinemática para resolver una de las velocidades y sustituirla por otra ecuación cinemática para obtener la segunda velocidad. Por lo tanto, resolvemos dos de las ecuaciones simultáneamente.
Solución
Primero resolvemos $v_0$ usando $x = x_0 + v_0t + \frac12 at^2$
Luego sustituimos $v_0$ en la ecuación $v = v_0 + at$ para hallar la velocidad final:
$$v = v_0 + at = 7133.3 m/s + (20.0 m/s^2)(120.0 s) = 9533.3 m/s.$$Explicación
Hay seis variables en desplazamiento, tiempo, velocidad y aceleración que describen el movimiento en una dimensión. Las condiciones iniciales de un problema dado pueden ser muchas combinaciones de estas variables. Debido a esta diversidad, las soluciones pueden no ser fáciles como simples sustituciones en una de las ecuaciones. Este ejemplo ilustra que las soluciones a la cinemática pueden requerir la resolución de dos ecuaciones cinemáticas simultáneas.
Con los fundamentos de la cinemática establecidos, podemos pasar a muchos otros ejemplos y aplicaciones interesantes. En el proceso de desarrollo de la cinemática, también hemos vislumbrado un enfoque general para la resolución de problemas que produce respuestas correctas y puntos de vista sobre las relaciones físicas. El siguiente nivel de complejidad en nuestros problemas cinemáticos involucra el movimiento de dos cuerpos interrelacionados, llamados problemas de persecución o de encuentro de dos cuerpos.
Problemas de persecución de dos cuerpos
Hasta este momento, hemos analizado ejemplos de movimientos que involucran un solo cuerpo.
Incluso para el problema con dos autos y las distancias de frenado en carreteras mojadas y secas, dividimos este problema en dos problemas separados para encontrar las respuestas. En un problema de persecución de dos cuerpos, los movimientos de los objetos están acoplados, es decir, el dato desconocido que buscamos depende del movimiento de ambos objetos. Para resolver estos problemas, escribimos las ecuaciones de movimiento para cada objeto y luego los resolvemos simultáneamente para encontrar la variable desconocida. Esto se ilustra en la figura 3.25.
El tiempo y la distancia requeridos para que el auto $1$ alcance el auto $2$ depende de la distancia inicial entre el auto $1$ y el auto $2$, las velocidades de ambos autos y la aceleración del auto $1$. Las ecuaciones cinemáticas que describen el movimiento de ambos autos deben ser resueltas para encontrar estas incógnitas.
Ejemplo 3.13
Un guepardo cazando una gacela
Un guepardo espera escondido detrás de un arbusto.
El guepardo ve una gacela corriendo a $10 m/s$. En el instante en que la gacela pasa al guepardo, el guepardo acelera desde el reposo a $4 m/s{2$ para atrapar a la gacela. (a) ¿Cuánto tiempo le toma al guepardo atrapar a la gacela? (b) ¿Cuál es el desplazamiento de la gacela y el guepardo?
Estrategia
Usamos el conjunto de ecuaciones de aceleración constante para resolver este problema. Como hay dos objetos en movimiento, tenemos ecuaciones de movimiento separadas que describen cada animal. Pero lo que vincula las ecuaciones es un parámetro común que tiene el mismo valor para cada animal. Si observamos de cerca el problema, está claro que el parámetro común es su posición $x$ en un momento posterior $t$. Como ambos comienzan en $x_0 = 0$, sus desplazamientos son los mismos en un momento posterior $t$, cuando el guepardo alcanza a la gacela. Si seleccionamos la ecuación de movimiento que resuelve el desplazamiento de cada animal, podemos establecer las ecuaciones entre sí y hallar el dato desconocido, que es el tiempo.
Solución
a. Ecuación para la gacela: La gacela tiene una velocidad constante, que es su velocidad promedio, ya que no se está acelerando. Por lo tanto, utilizamos la Ecuación 3.10 con $x_0 = 0$:
$$x = x_0 + \={v}t = \={v}t$$Ecuación para el guepardo: El guepardo está acelerando desde el reposo, por lo que usamos la ecuación 3.13 con $x_0 = 0$ y $v_0 = 0$:
Ahora tenemos una ecuación de movimiento para cada animal con un parámetro común, que puede eliminarse para encontrar la solución. En este caso, resolvemos para $t$:
$$x = \={v}t = \frac12 at^2\\ \\ t = \frac{2\={v}}{a}$$La gacela tiene una velocidad constante de $10 m/s$, que es su velocidad promedio. La aceleración del guepardo es de $4 m/s^2$. Evaluando $t$, el tiempo para que el guepardo alcance a la gacela, tenemos
$$t = \frac{2\={v}}{a} = \frac{2(10)}{4} = 5s$$b. Para obtener el desplazamiento, utilizamos la ecuación de movimiento para el guepardo o la gacela, ya que ambos deberían dar la misma respuesta.
Desplazamiento del guepardo:
$$x = \frac12 at^2 = \frac12 (4)(5)^2 = 50 m$$Desplazamiento de la gacela:
$$x =\={v}t = 10(5) = 50 m$$Vemos que ambos desplazamientos son iguales, como se esperaba.
Explicación
Es importante analizar el movimiento de cada objeto y usar las ecuaciones cinemáticas apropiadas para describir el movimiento individual. También es importante tener una buena perspectiva visual del problema de encuentro de dos cuerpos para ver el parámetro común que vincula el movimiento de ambos objetos.
 Comprueba tu aprendizaje 3.6
Comprueba tu aprendizaje 3.6
Caída libre
Una aplicación interesante de las Ecuaciones 3.4 a la 3.14 se llama caída libre, que describe el movimiento de un objeto que cae en un campo gravitatorio, como cerca de la superficie de la Tierra u otros objetos celestes de tamaño planetario. Supongamos que el cuerpo está cayendo en línea recta perpendicular a la superficie, por lo que su movimiento es unidimensional.
Por ejemplo, podemos estimar la profundidad de un pozo vertical de la mina arrojando una roca en él y escuchando que la roca toque el fondo. Pero "caer", en el contexto de la caída libre, no implica necesariamente que el cuerpo se mueva de una altura mayor a una altura menor. Si una pelota se lanza hacia arriba, las ecuaciones de caída libre se aplican por igual a su ascenso, así como su descenso.
Gravedad
El hecho más notable e inesperado sobre la caída de objetos es que si la resistencia del aire y la fricción son insignificantes, entonces, en un lugar determinado, todos los objetos caen hacia el centro de la Tierra con la misma aceleración constante, independientemente de su masa. Este hecho determinado experimentalmente es inesperado porque estamos tan acostumbrados a los efectos de la resistencia al aire y la fricción que esperamos que los objetos ligeros caigan más lentamente que los pesados. Hasta que Galileo Galilei (1564-1642) demostró lo contrario, la gente creía que un objeto más pesado tiene una mayor aceleración en una caída libre. Ahora sabemos que este no es el caso. En ausencia de resistencia del aire, los objetos pesados llegan al suelo al mismo tiempo que los objetos más ligeros cuando se los deja caer desde la misma altura (Figura 3.26).
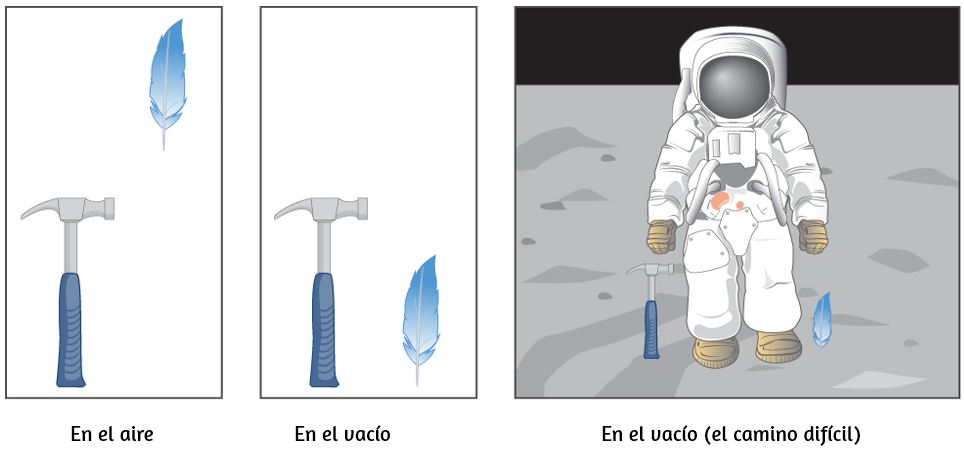
En el mundo real, la resistencia del aire puede hacer que un objeto más ligero caiga más lento que un objeto más pesado del mismo tamaño. Una pelota de tenis llega al suelo después de una pelota de béisbol que inician su caída al mismo tiempo (Puede ser difícil observar la diferencia si la altura no es grande). La resistencia del aire se opone al movimiento de un objeto a través del aire y la fricción entre objetos, como entre la ropa y una tolva de lavandería o entre una piedra y una piscina.
Para las situaciones ideales de estos primeros capítulos, un objeto que cae sin resistencia o fricción se define como en caída libre. La fuerza de la gravedad hace que los objetos caigan hacia el centro de la Tierra.
Por lo tanto, la aceleración de los objetos en caída libre se llama aceleración debido a la gravedad. La aceleración debido a la gravedad es constante, lo que significa que podemos aplicar las ecuaciones cinemáticas a cualquier objeto que caiga donde la resistencia del aire y la fricción sean insignificantes. Esto nos abre una amplia clase de situaciones interesantes.
La aceleración debida a la gravedad es tan importante que a su magnitud se le da su propio símbolo, $g$. Es constante en cualquier ubicación dada en la Tierra y tiene el valor promedio
$$g = 9.81 m/s^2 (32.2 ft/s^2)$$Aunque g varía de $9.78 m/s^2$ a $9.83 m/s^2$, dependiendo de la latitud, la altitud, las formaciones geológicas subyacentes y la topografía local, utilizaremos un valor promedio de $9.8 m/s^2$ redondeado a dos cifras significativas en este texto a menos que se especifique lo contrario.
Despreciando estos efectos sobre el valor de $g$ como resultado de la posición en la superficie de la Tierra, así como los efectos resultantes de la rotación de la Tierra, tomamos la dirección de la aceleración debido a la gravedad hacia abajo (hacia el centro de la Tierra). De hecho, su dirección define lo que llamamos vertical.
Ten en cuenta que si la aceleración $a$ en las ecuaciones cinemáticas tiene el valor $+g$ o $-g$ depende de cómo definamos nuestro sistema de coordenadas. Si definimos la dirección ascendente como positiva, entonces $a = -g = -9.8 m/s^2$, y si definimos la dirección descendente como positiva, entonces $a = g = 9.8 m/s^2$.
Movimiento unidimensional que involucra la gravedad
La mejor manera de ver las características básicas del movimiento que involucra la gravedad es comenzar con las situaciones más simples y luego avanzar hacia las más complejas. Entonces, comenzamos considerando movimientos ascendentes y descendentes sin resistencia ni fricción.
Estas suposiciones significan que la velocidad (si hay alguna) es vertical. Si se cae un objeto, sabemos que la velocidad inicial es cero cuando está en caída libre. Cuando el objeto ha dejado contacto con lo que haya sostenido o lo ha arrojado, el objeto está en caída libre. Cuando se arroja el objeto, tiene la misma velocidad inicial en caída libre que antes de su lanzamiento.
Cuando el objeto entra en contacto con el suelo o cualquier otro objeto, ya no está en caída libre y su aceleración $g$ ya no es válida. En estas circunstancias, el movimiento es unidimensional y tiene una aceleración constante de magnitud $g$. Representamos el desplazamiento vertical con el símbolo $y$.
Supongamos que la aceleración es igual a $-g$.
Estrategia de resolución de problemas: caída libre
- Decide sobre el signo de la aceleración de la gravedad. En 3.15 a 3.17, la aceleración $g$ es negativa, que dice que la dirección positiva es hacia arriba y la negativa hacia abajo. En algunos problemas, puede ser útil tener la aceleración $g$ positiva.
- Dibuja un boceto del problema. Ayuda a ver la física involucrada.
- Registra los datos conocidos y las incógnitas del problema. Ayuda a diseñar una estrategia para seleccionar las ecuaciones apropiadas para resolver el problema.
- Decide cuál de la ecuaciones 3.15 a 3.17 vas a utilizar para hallar el valor de las incógnitas.
Ejemplo 3.14
Caída libre de una bola
La Figura 3.27 muestra las posiciones de una pelota, a intervalos de $1 s$, con una velocidad inicial de $4.9 m/s^2$ hacia abajo, que se lanza desde la parte superior de un edificio de 98 m de altura.
(a) ¿Cuánto tiempo transcurre antes de que la pelota llegue al suelo? (b) ¿Cuál es la velocidad cuando llega al suelo?
Estrategia
Elige el origen en la parte superior del edificio con la dirección positiva hacia arriba y la dirección negativa hacia abajo. Para encontrar el tiempo cuando la posición es $-98 m$, usamos la Ecuación 3.16, con $y_0 = 0, v_0 = -4.9 m/s$, y $g = 9.8 m/s^2$.

Solución
a. Sustituye los valores dados en la ecuación:
$$y = y_0 + v_0t − \frac12 gt^2$$Simplificando
$$t^2 + t - 20 = 0$$Esta es una ecuación cuadrática con raíces $t = -5.0$ s y $t = 4.0s$. La raíz positiva es la que nos interesa, ya que el tiempo $t = 0$ es el momento en que se lanza la pelota en la parte superior del edificio (El tiempo $t = -5.0 s$ representa el hecho de que una pelota lanzada hacia arriba desde el suelo habría estado en el aire durante $5.0 s$ cuando pasó por la parte superior del edificio moviéndose hacia abajo a $4.9 m/s$).
b. Usando la Ecuación 3.15, tenemos
$$v = v_0 - gt = -4.9 m/s - (9.8 m/s^2)(4.0 s) = - 44.1 m/s.$$Explicación
Para situaciones en las que se obtienen dos raíces a partir de una ecuación cuadrática en la variable tiempo, debemos observar el significado físico de ambas raíces para determinar cuál es la correcta. Como $t = 0$ corresponde al momento en que se liberó la pelota, la raíz negativa correspondería a un tiempo anterior a la liberación de la pelota, lo cual no es físicamente significativo. Cuando la pelota golpea el suelo, su velocidad no es inmediatamente cero, pero tan pronto como la pelota interactúa con el suelo, su aceleración no es g y acelera con un valor diferente en un corto tiempo a velocidad cero. Este problema muestra cuán importante es establecer el sistema de coordenadas correcto y mantener constantes los signos de $g$ en las ecuaciones cinemáticas.
Ejemplo 3.15
Movimiento vertical de una pelota de béisbol
Un bateador golpea una pelota de béisbol directamente hacia arriba en el plato de home y la pelota es atrapada $5.0 s$ después de ser golpeada (Figura 3.28). (a) ¿Cuál es la velocidad inicial de la pelota? (b) ¿Cuál es la altura máxima que alcanza la pelota? (c) ¿Cuánto tiempo lleva alcanzar la altura máxima? (d) ¿Cuál es la aceleración en la parte superior de su camino? (e) ¿Cuál es la velocidad de la pelota cuando está atrapada? Supón que la pelota es golpeada y atrapada en el mismo lugar.
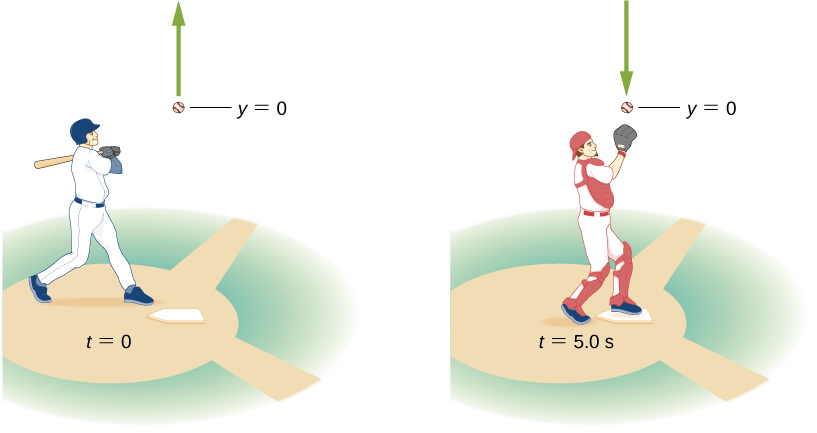
Estrategia
Elije un sistema de coordenadas con un eje $y$ positivo hacia arriba y con un origen que esté en el lugar donde se golpea y atrapa la pelota.
Solución
a. Con la ecuación 3.16 obtenemos
$$y = y_0 + v_0t − \frac12 gt^2\\ 0 = 0 - v_0(5.0 s) − \frac12 (9.8 m/s^2)(5.0 s)^2$$que nos da $v_0 = 24.5 m/s$.
b. En la altura máxima, $v = 0$. Con $v_0 = 24.5 m/s$, la ecuación 3.17 da
$$v^2 = v_0^2 − 2g(y − y_0)\\ 0 = (24.5m/s)^2 − 2(9.8 m/s^2)(y − 0)\\ y = 30.6m.$$c. Para encontrar el tiempo cuando $v = 0$, usamos la Ecuación 3.15:
$$v = v_0 - gt\\ 0 = 24.5 m/s - (9.8 m/s^2)t$$El resultado es $t = 2.5 s$. Como la pelota se eleva durante $2.5 s$, el tiempo de caída es de $2.5 s$.
d. La aceleración es de $9.8 m/s^2$ en todas partes, incluso cuando la velocidad es cero en la parte superior de la ruta. Aunque la velocidad es cero en la parte superior, está cambiando a una rata de $9.8 m/s^2$ hacia abajo.
e. La velocidad en $t = 5.0 s$ se puede determinar con la Ecuación 3.15:
Explicación
La pelota vuelve con la velocidad que tenía cuando salió. Esta es una propiedad general de caída libre para cualquier velocidad inicial. Usamos una ecuación única para pasar de lanzar a atrapar, y no tuvimos que dividir el movimiento en dos segmentos, hacia arriba y hacia abajo. Estamos acostumbrados a pensar que el efecto de la gravedad es crear una caída libre hacia la Tierra. Es importante entender, como se ilustra en este ejemplo, que los objetos que se mueven hacia arriba desde la Tierra también se encuentran en un estado de caída libre.
 Comprueba tu aprendizaje 3.4
Comprueba tu aprendizaje 3.4
Ejemplo 3.16
Cohete Booster
Un pequeño cohete con un amplificador (booster) se dispara y se dirige directamente hacia arriba. Cuando se encuentra a una altura de $5.0 km$ y una velocidad de $200.0 m/s$, libera su amplificador.
(a) ¿Cuál es la altura máxima que alcanza el amplificador? (b) ¿Cuál es la velocidad del amplificador a una altura de $6.0 km$? Desprecia la resistencia del aire.
Estrategia
Necesitamos seleccionar el sistema de coordenadas para la aceleración de la gravedad, que tomamos como negativo hacia abajo. Se nos da la velocidad inicial del amplificador y su altura. Consideramos el punto de liberación como el origen. Sabemos que la velocidad es cero en la posición máxima dentro del intervalo de aceleración; por lo tanto, la velocidad del amplificador es cero en su altura máxima, por lo que podemos utilizar esta información también. A partir de estas observaciones, utilizamos la ecuación 3.17, que nos da la altura máxima del amplificador. También usamos la Ecuación 3.17 para dar la velocidad a $6.0 km$. La velocidad inicial del amplificador es de $200.0 m/s$.
Solución
a. De la ecuación 3.17, $v^2 = v_0^2 - 2g(y - y_0)$. Con $v = 0$ y $y_0 = 0$, podemos resolver para $y$:
$$y = \frac{(2 \times 10^2> m/s)^2}{-2g} = \frac{v_0^2}{-2(9.8 m/s^2)} = 2040.8m$$Esta solución proporciona la altura máxima del amplificador en nuestro sistema de coordenadas, que tiene su origen en el punto de liberación, por lo que la altura máxima del amplificador es de aproximadamente $7,0 km$.
b. Una altitud de 6$.0 km $ corresponde a $y = 1.0 \times 10^3 m$ en el sistema de coordenadas que estamos usando. Las otras condiciones iniciales son $y_0 = 0$, y $v_0 = 200.0 m/s$.
Tenemos, de la Ecuación 3.17,
$$v^2 = (200.0 m/s)^2 - 2(9.8 m/s^2)(1.0 \times 10^3 m) \implies v = \pm 142.8 m/s$$Explicación
Tenemos una solución positiva y negativa en (b). Dado que nuestro sistema de coordenadas tiene la dirección positiva hacia arriba, los $+142.8 m/s$ corresponden a una velocidad positiva hacia arriba a $6000 m$ durante el tramo ascendente de la trayectoria del amplificador.
El valor $v = -142.8 m/s$ corresponde a la velocidad a $6000 m$ en la pata descendente.
Este ejemplo también es importante porque a un objeto se le da una velocidad inicial en el origen de nuestro sistema de coordenadas, pero el origen está a una altitud sobre la superficie de la Tierra, que debe tenerse en cuenta al formular la solución.
Para terminar este apartado, observa el vídeo de la página siguiente, sobre la gravedad, de la agencia espacial europea.
Video
Encontrando la velocidad y el desplazamiento a partir de la aceleración
Esta sección asume que tienes suficientes antecedentes en cálculo para estar familiarizado con la integración. En velocidad y aceleración promedio e instantánea, presentamos las funciones cinemáticas usando la derivada. Tomando la derivada de la función de posición encontramos la función de velocidad, y del mismo modo tomando la derivada de la función de velocidad encontramos la función de aceleración. Usando el cálculo integral, podemos trabajar hacia atrás y calcular la función de velocidad desde la función de aceleración, y la función de posición desde la función de velocidad.
Ecuaciones cinemáticas del cálculo integral
Comencemos con una partícula con aceleración $a(t)$, la cual es una función conocida. Como la derivada con respecto al tiempo de la función de velocidad es la aceleración,
$$\frac{d}{dt}v(t) = a(t)$$podemos tomar la integral indefinida de ambos lados, encontrando
$$\int \frac{d}{dt}v(t)dt = \int a(t)dt + C_1$$donde $C_1$ es una constante de integración. Como $\displaystyle\int \frac{d}{dt}v(t)dt = v(t)$, la velocidad viene dada por la siguiente expresión:
Del mismo modo, la derivada de la función de posición con respecto al tiempo es la función de velocidad,
$$\frac{d}{dt} x(t) = v(t)$$Por lo tanto, podemos usar las mismas manipulaciones matemáticas que acabamos de usar y encontrar
donde $C_2$ es una segunda constante de integración.
Podemos derivar las ecuaciones cinemáticas para una aceleración constante usando estas integrales. Con $a(t) = a$ constante, y haciendo la integración en la Ecuación 3.18, encontramos
$$v(t) = \int adt + C_1 = at + C_1$$Si la velocidad inicial es $v(0) = v_0$, entonces
$$v_0 = 0 + C_1$$Entonces, $C_1 = v_0 y$
$$v(t) = v_0 + at$$que es la Ecuación 3.12. al sustituir esta expresión en la Ecuación 3.19 obtenemos
$$x(t) = \int (v_0 + at)dt + C_2$$Al hacer la integración, encontramos
$$x(t) = v_0t + \frac12 at^2 + C_2$$Si $x(0) = x_0$, tenemos
$$x_0 = 0 + 0 + C_2$$Entonces, $C_2 = x_0$. Sustituyendo de nuevo en la ecuación por $x(t)$, finalmente tenemos
que es la Ecuación 3.13.
Ejemplo 3.17
Movimiento de una lancha
Una lancha a motor viaja a una velocidad constante de $5.0 m/s$ cuando comienza a desacelerarse para llegar al muelle. Su aceleración es $a(t) = -(1/4)t m/s^2$. (a) ¿Cuál es la función de velocidad de la lancha a motor? (b) ¿A qué hora la velocidad llega a cero? (c) ¿Cuál es la función de posición de la lancha a motor? (d) ¿Cuál es el desplazamiento de la lancha a motor desde el momento en que comienza a desacelerar hasta cuando la velocidad es cero? (e) Grafica las funciones de velocidad y posición.
Estrategia
(a) Para obtener la función de velocidad, debemos integrar y utilizar las condiciones iniciales para encontrar la constante de integración. (b) Establecemos la función de velocidad igual a cero y resolvemos para $t$. (c) De manera similar, debemos integrar para encontrar la función de posición y usar las condiciones iniciales para encontrar la constante de integración. (d) Dado que la posición inicial se toma como cero, solo tenemos que evaluar la función de posición en $t = 0$
Solución
Consideramos que $t = 0$ es el momento en que el barco comienza a desacelerar.
a. De la función de aceleración podemos resolver la Ecuación 3.18 obteniendo $v(t)$:
$$v(t) = \int a(t)dt + C_1 = \int -\frac14 tdt + C_1 = -\frac18 t^2 + C_1$$En $t = 0$ tenemos $v(0) = 5.0 m/s = 0 + C_1$, por lo que $C_1 = 5.0 m/s $ y $v(t) = 5.0 m/s - 18t^2$.
b. $v(t) = 0 = 5.0 m/s - 18t^2 \implies t = 6.3 s$
c. Resolviendo la ecuación 3.19:
$$x(t) = \int v(t)dt + C_2 = \int (5.0-\frac18 t^2)dt + C_2 = 5.0t - \frac{1}{24}t^3 + C_2$$En $t = 0$, establecemos $x(0) = 0 = x_0$, ya que solo estamos interesados en el desplazamiento desde cuando el barco comienza a desacelerar. Tenemos
$$x(0) = 0 = C_2$$Por lo tanto, la ecuación para la posición es
$$x(t) = 5.0t - \frac{1}{24}t^3$$d. Como la posición inicial se toma como cero, solo tenemos que evaluar $x(t)$ cuando la velocidad es cero. Esto ocurre en $t = 6.3 s$. Por lo tanto, el desplazamiento es
$$x(6.3) = 5.0(6.3) − \frac{1}{24}(6.3)^3 = 21.1 m$$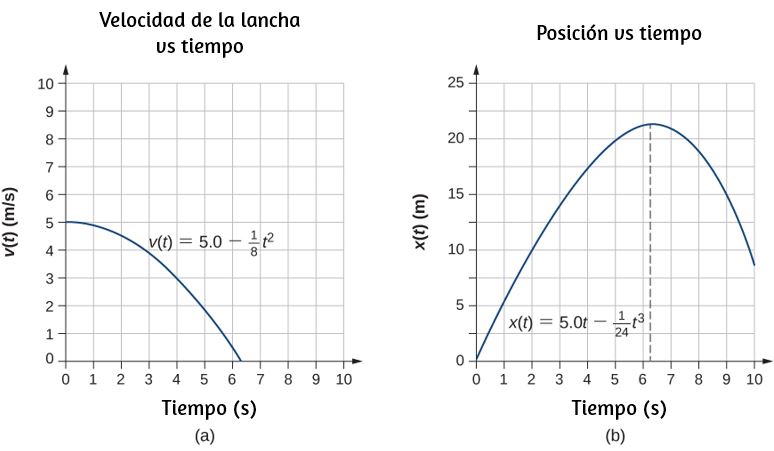
Explicación
a) La velocidad del bote a motor en función del tiempo. La lancha a motor disminuye su velocidad a cero en 6.3 s. En momentos más grandes que esto, la velocidad se vuelve negativa, es decir, el barco está invirtiendo la dirección. (b) Posición de la lancha motora en función del tiempo. En $t = 6.3 s$, la velocidad es cero y el barco se ha detenido.
En momentos mayores que esto, la velocidad se vuelve negativa, es decir, si la embarcación continúa moviéndose con la misma aceleración, invierte la dirección y se dirige hacia donde se originó.
La función de aceleración es lineal en el tiempo, por lo que la integración implica polinomios simples. En la figura 3.30, vemos que si extendemos la solución más allá del punto en que la velocidad es cero, la velocidad se vuelve negativa y el barco invierte la dirección. Esto nos dice que las soluciones pueden brindarnos información fuera de nuestro interés inmediato y debemos tener cuidado al interpretarlas.
 Comprueba tu aprendizaje 3.8
Comprueba tu aprendizaje 3.8
El siguiente objeto interactivo, diseñado por Juan Guillermo Rivera Berrío, es un puzle giratorio, haz clic sobre las piezas para rotarlas, hasta armar la imagen. Son cuatro imágenes relacionadas con el tema de caida libre.
Cinemática: Movimiento
en dos y tres dimensiones
Video publicado en TikTok, en el canal @vismart:edu
Introducción

Para dar una descripción completa de la cinemática, debemos explorar el movimiento en dos y tres dimensiones. Después de todo, la mayoría de los objetos en nuestro universo no se mueven en línea recta; más bien, siguen caminos curvos. Desde los balones de fútbol pateados hasta las trayectorias de vuelo de los pájaros hasta los movimientos orbitales de los cuerpos celestes y hasta el flujo de plasma sanguíneo en tus venas, la mayoría del movimiento sigue trayectorias curvas.
Afortunadamente, el tratamiento del movimiento en una dimensión en el capítulo anterior nos ha dado una base sobre la cual construir, ya que los conceptos de posición, desplazamiento, velocidad y aceleración definidos en una dimensión se pueden expandir a dos y tres dimensiones.
Considera las Flechas Rojas, también conocidos como el equipo de aeroacrobacia de la Royal Air Force del Reino Unido. Cada jet sigue una trayectoria curva única en el espacio aéreo tridimensional, además de tener una velocidad y aceleración únicas. Por lo tanto, para describir el movimiento de cualquiera de las aeronaves con precisión, debemos asignar a cada jet un vector de posición único en tres dimensiones, así como un vector único de velocidad y aceleración. Podemos aplicar las mismas ecuaciones básicas para el desplazamiento, la velocidad y la aceleración que obtuvimos en el capítulo anterior para describir el movimiento de las aeronaves en dos y tres dimensiones, pero con algunas modificaciones, en particular, la inclusión de vectores.
En este capítulo también exploraremos dos tipos especiales de movimiento en dos dimensiones: movimiento parabólico y movimiento circular. Por último, concluimos con una discusión sobre el movimiento relativo. En la imagen de apertura del capítulo, cada jet tiene un movimiento relativo con respecto a cualquier otro jet en el grupo o a las personas que observan el espectáculo aéreo en el suelo.
Vectores de desplazamiento y velocidad
El desplazamiento y la velocidad en dos o tres dimensiones son extensiones directas de las definiciones unidimensionales. Sin embargo, ahora son cantidades vectoriales, por lo que los cálculos deben seguir las reglas del álgebra vectorial, no del escalar.
Vector de desplazamiento
Para describir el movimiento en dos y tres dimensiones, primero debemos establecer un sistema de coordenadas y una convención para los ejes.
Generalmente usamos las coordenadas $x, y$, y $z$ para ubicar una partícula en el punto $P(x, y, z)$ en tres dimensiones. Si la partícula se está moviendo, las variables $x, y$, y $z$ son funciones del tiempo ($t$):
El vector de posición desde el origen del sistema de coordenadas hasta el punto $P$ es $\bold{\vec{r}}(t)$. En la notación vectorial unitaria, introducida en los Sistemas de coordenadas y componentes de un vector, $\bold{\vec{r}}(t)$ es
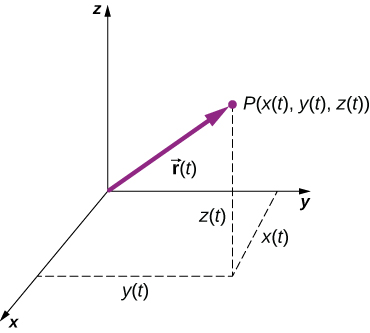
Con nuestra definición de la posición de una partícula en el espacio tridimensional, podemos formular el desplazamiento tridimensional. La figura 4.3 muestra una partícula en el momento $t_1$ ubicado en $P_1$ con el vector de posición $\bold{\vec{r}}(t_1)$. En un momento posterior $t_2$, la partícula se localiza en $P_2$ con el vector de posición $\bold{\vec{r}}(t_2)$. El vector de desplazamiento $\Delta\bold{\vec{r}}$ se encuentra restando $\bold{\vec{r}}(t_1)$ de $\bold{\vec{r}}(t_2)$.:
La suma de vectores se discutió en el capítulo II. Ten en cuenta que esta es la misma operación que hicimos en una dimensión, pero ahora los vectores están en espacio tridimensional.
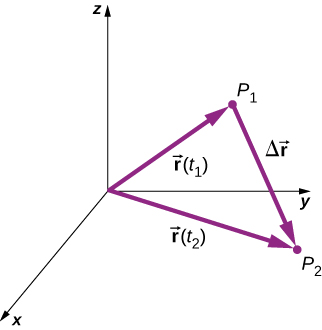
Los siguientes ejemplos ilustran el concepto de desplazamiento en múltiples dimensiones.
Ejemplo 4.1
Satélite en órbita polar
Un satélite se encuentra en una órbita polar circular alrededor de la Tierra a una altitud de $400 km$, lo que significa que pasa directamente por encima de los polos norte y sur. ¿Cuál es la magnitud y dirección del vector de desplazamiento desde cuando está directamente sobre el Polo Norte hasta cuando está a $-45\degree$ de latitud?
Estrategia
Hacemos una foto del problema para visualizar la solución gráficamente. Esto ayudará en nuestra comprensión del desplazamiento. Luego usamos vectores unitarios para hallar el desplazamiento.
Solución
La figura 4.4 muestra la superficie de la Tierra y un círculo que representa la órbita del satélite. Aunque los satélites se mueven en un espacio tridimensional, siguen trayectorias de elipses, que se pueden graficar en dos dimensiones. Los vectores de posición se extraen del centro de la Tierra, que tomamos como el origen del sistema de coordenadas, con el eje y como el norte y el eje $x$ como el este. El vector entre ellos es el desplazamiento del satélite. Tomamos el radio de la Tierra como $6370 km$, por lo que la longitud de cada vector de posición es $6770 km$.
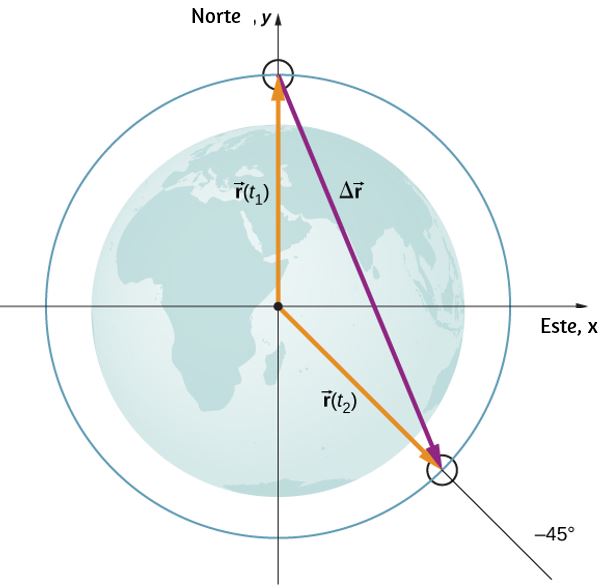
En la notación vectorial unitaria, los vectores de posición son
$$\bold{\vec{r}}(t_1) = 6770km\^{\bold{j}}\\ \bold{\vec{r}}(t_2) = 6770km(cos45\degree)\^{\bold{i}} + 6770km(sin(−45\degree))\^{\bold{j}}$$Evaluando el seno y el coseno, tenemos
$$\bold{\vec{r}}(t_1) = 6770km\^{\bold{j}}\\ \bold{\vec{r}}(t_2) = 4787\^{\bold{i}} + 4787\^{\bold{j}}$$Ahora, podemos encontrar $\Delta\bold{\vec{r}}$, el desplazamiento del satélite:
$$\Delta \bold{\vec{r}} = \bold{\vec{r}}(t_2) - \bold{\vec{r}}(t_1) = 4787\^{\bold{i}} −11,557\^{\bold{j}}$$La magnitud del desplazamiento es $|\Delta\bold{\vec{r}}| = \sqrt{(4787)^2 + (−11,557)^2} = 12,509 km$. El ángulo que hace el desplazamiento con el eje $x$ es $$\theta = tan^{-1}\Big(\frac{−11,557}{4787}\Big) = - 67.5\degree$$
Explicación
Trazar el desplazamiento proporciona información y significado a la solución de vector unitario del problema. Al trazar el desplazamiento, necesitamos incluir sus componentes, así como su magnitud y el ángulo que forma con un eje elegido, en este caso, el eje $x$ (Figura 4.5).
Ten en cuenta que el satélite tomó un camino curvo a lo largo de su órbita circular para llegar desde su posición inicial a su posición final en este ejemplo. También podría haber recorrido $4787 km$ al este, luego $11,557 km$ al sur para llegar al mismo lugar. Ambas rutas son más largas que la longitud del vector de desplazamiento. De hecho, el vector de desplazamiento proporciona la ruta más corta entre dos puntos en una, dos o tres dimensiones.
Muchas aplicaciones en física pueden tener una serie de desplazamientos, como se discutió en el capítulo anterior. El desplazamiento total es la suma de los desplazamientos individuales, solo que esta vez, debemos tener cuidado, porque estamos agregando vectores. Ilustramos este concepto con un ejemplo de movimiento browniano.
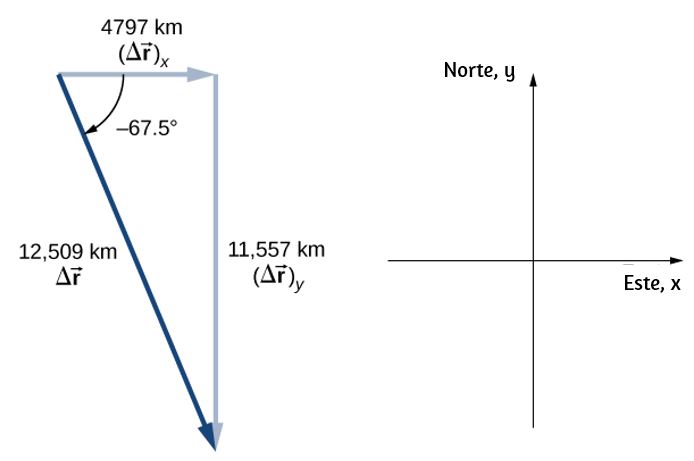
Movimiento browniano
El movimiento browniano es un movimiento aleatorio caótico de partículas suspendidas en un fluido, como resultado de colisiones con las moléculas del fluido. Este movimiento es tridimensional.
Los desplazamientos en orden numérico de una partícula sometida a movimiento Browniano podrían verse como los mostrados en la figura 4.6, en micrómetros:
$$\Delta \bold{\vec{r}}_1 = 2.0\^{\bold{i}} + \^{\bold{j}} + 3.0\^{\bold{k}}\\ \Delta \bold{\vec{r}}_2 = -\^{\bold{i}} + 3.0\^{\bold{k}}\\ \Delta \bold{\vec{r}}_3 = -3.0\^{\bold{i}} + \^{\bold{j}} + 2.0\^{\bold{k}}$$¿Cuál es el desplazamiento total de la partícula desde el origen?
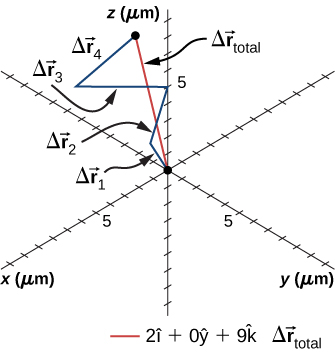
Solución
Escribimos la sumatoria de los desplazamientos y, luego, sumamos sus componentes rectangulares:
$$\begin{split} \Delta \bold{\vec{r}}_{\text{Total}} &= \sum \Delta \bold{\vec{r}}_i\\ &= \Delta \bold{\vec{r}}_1 + \Delta \bold{\vec{r}}_2 + \Delta \bold{\vec{r}}_3 + \Delta \bold{\vec{r}}_4\\ &= (2.0 − 1.0 + 4.0 − 3.0)\^{\bold{i}} + (1.0 + 0 − 2.0 + 1.0)\^{\bold{j}} \\ & \;\;\;\;\; + (3.0 + 3.0 + 1.0 + 2.0)\^{\bold{k}}\\ &= 2.0\^{\bold{i}} + 0\^{\bold{j}} +9.0\^{\bold{k}}\mu m \end{split}$$Para completar la solución, expresamos el desplazamiento con su magnitud y dirección,
$$|\Delta \bold{\vec{r}}_{\text{Total}}| = \sqrt{ 2.0^2 + 0^2 + 9.0^2} = 9.2 \mu m, \theta = tan^{−1}\big(\frac92\big) = 77\degree$$con respecto al eje $x$ en el plano $xz$.
Explicación
De la figura podemos ver que la magnitud del desplazamiento total es menor que la suma de las magnitudes de los desplazamientos individuales.

|
Esta es una simulación del movimiento browniano de $5$ partículas (amarillas) que colisionan con un gran conjunto de $800$ partículas. Las partículas amarillas dejan $5$ rastros azules de movimiento aleatorio y uno de ellos tiene un vector de velocidad rojo (crédito: wikipedia) |
Vector de velocidad
En el capítulo anterior encontramos la velocidad instantánea calculando la derivada de la función de posición con respecto al tiempo. Podemos hacer la misma operación en dos y tres dimensiones, pero usamos vectores. El vector de velocidad instantánea es ahora
Veamos la orientación relativa del vector de posición y el vector de velocidad gráficamente. En la figura 4.7 mostramos los vectores $\bold{\vec{r}}(t)$ y $\bold{\vec{r}}(t + \Deltat)$, que dan la posición de una partícula moviéndose a lo largo de un camino representado por la línea gris. Como Δt tiende a cero, el vector de velocidad, dado por la ecuación 4.4, se vuelve tangente al camino de la partícula en el tiempo $t$.
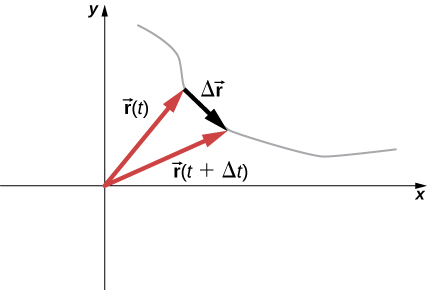
La ecuación 4.4 también se puede escribir en términos de los componentes rectangulares de $\bold{\vec{v}}(t)$. Ya que
$$\bold{\vec{r}}(t) = x(t)\^{\bold{i}} + y(t)\^{\bold{j}} + z(t)\^{\bold{k}}$$podemos escribir
donde
Si solo la velocidad promedio es preocupante, tenemos el vector equivalente a la velocidad promedio unidimensional para dos y tres dimensiones:
Ejemplo 4.3
Calculando el vector velocidad
La función de posición de una partícula es $\bold{\vec{r}}(t) = 2.0t^2\^{\bold{i}} + (2.0 + 3.0t)\^{\bold{j}} + 5.0t\^{\bold{k}} m$. (a) ¿Cuál es la rapidez y la velocidad instantánea en $t = 2.0 s$? (b) ¿Cuál es la velocidad promedio entre $1.0 s$ y $3.0 s$?
Solución
Usando la Ecuación 4.5 y la Ecuación 4.6, y tomando la derivada de la función de posición con respecto al tiempo, encontramos
$(a) v(t) = \frac{dr(t)}{dt} = 4.0t\^{\bold{i}} + 3.0\^{\bold{j}} + 5.0\^{\bold{k}} m/s$
$\bold{\vec{v}}(2.0s) = 8.0\^{\bold{i}} + 3.0\^{\bold{j}} + 5.0\^{\bold{k}} m/s$
Rapidez $|\bold{\vec{v}}(2.0s)| = \sqrt{8^2 + 3^2 + 5^2} = 9.9 m/s$
(b) de la ecuación 4.7
$$\begin{split} \bold{\vec{v}}_{\text{prom}} &= \frac{\bold{\vec{r}}(t_2) - \bold{\vec{r}}_(t_1)}{t_2-t_1}\\ &= \frac{\bold{\vec{r}}(3.0s) - \bold{\vec{r}}_(1.0s)}{3.0s-1.0s}\\ &= \frac{(18\^{\bold{i}} +11\^{\bold{j}}+15\^{\bold{k}}) - (2\^{\bold{i}} + 5\^{\bold{j}} + 5\^{\bold{k}})}{2.0s}\\ &= 8.0\^{\bold{i}} + 3.0\^{\bold{j}} + 5.0\^{\bold{k}}m/s \end{split}$$Explicación
Vemos que la velocidad promedio es la misma que la velocidad instantánea en $t = 2.0 s$, como resultado de que la función de velocidad es lineal. Este no es el caso en general. De hecho, la mayoría de las veces, las velocidades instantáneas y promedio no son las mismas.
 Comprueba tu aprendizaje 4.1
Comprueba tu aprendizaje 4.1
La independencia de los movimientos perpendiculares
Cuando miramos las ecuaciones tridimensionales para la posición y la velocidad escritas en notación vectorial unitaria, Ecuación 4.2 y Ecuación 4.5, vemos que los componentes de estas ecuaciones son funciones de tiempo separadas y únicas que no dependen una de la otra. El movimiento a lo largo de la dirección $x$ no tiene parte de su movimiento a lo largo de las direcciones $y$ y $z$, y de manera similar para los otros dos ejes de coordenadas. Por lo tanto, el movimiento de un objeto en dos o tres dimensiones se puede dividir en movimientos separados e independientes a lo largo de los ejes perpendiculares del sistema de coordenadas en el que tiene lugar el movimiento.
Para ilustrar este concepto con respecto al desplazamiento, considere una mujer caminando desde el punto $A$ al punto $B$ en una ciudad con bloques cuadrados.
La mujer que toma el camino de $A$ a $B$ puede caminar hacia el este por tantas cuadras y luego hacia el norte (dos direcciones perpendiculares) por otro grupo de bloques hasta que llegue a B. Lo único que camina hacia el este es afectado solo por su movimiento hacia el este. De manera similar, cuán lejos camina hacia el norte solo se ve afectada por su movimiento hacia el norte.
Un ejemplo que ilustra la independencia de los movimientos verticales y horizontales está dado por dos pelotas de béisbol. Una pelota de béisbol se cae del soporte.
En el mismo instante, otra se lanza horizontalmente desde la misma altura y sigue una trayectoria curva. Un estroboscopio captura las posiciones de las bolas a intervalos de tiempo fijos a medida que caen (Figura 4.8).
Es notable que por cada destello del estroboscopio, las posiciones verticales de las dos bolas son las mismas. Esta similitud implica que el movimiento vertical es independiente de si la bola se mueve horizontalmente. (Suponiendo que no hay resistencia del aire, el movimiento vertical de un objeto que cae está influenciado solo por la gravedad, no por fuerzas horizontales).
El examen cuidadoso de la pelota lanzada horizontalmente muestra que viaja la misma distancia horizontal entre los flashes. Esto se debe a que no hay fuerzas adicionales en la bola en la dirección horizontal después de que se lanza. Este resultado significa que la velocidad horizontal es constante y no se ve afectada por el movimiento vertical ni por la gravedad (que es vertical). Ten en cuenta que este caso es cierto solo para condiciones ideales.
En el mundo real, la resistencia del aire afecta la velocidad de las bolas en ambas direcciones.
La trayectoria curva bidimensional de la bola lanzada horizontalmente se compone de dos movimientos unidimensionales independientes (horizontal y vertical). La clave para analizar dicho movimiento, llamado movimiento de proyectil, es resolverlo en movimientos a lo largo de direcciones perpendiculares. La resolución del movimiento bidimensional en componentes perpendiculares es posible porque los componentes son independientes.
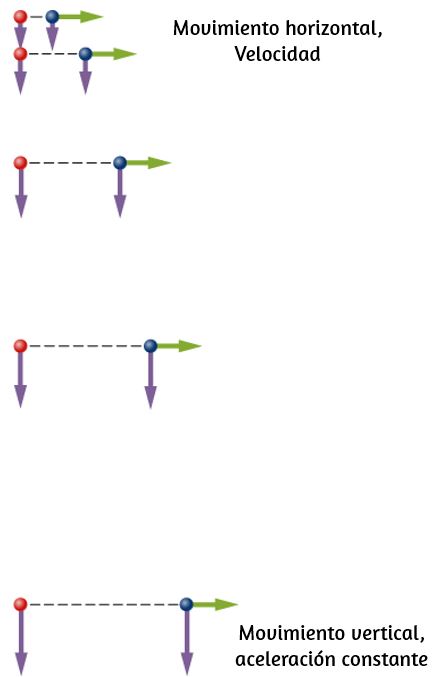
Vector de aceleración
Aceleración instantánea
Además de obtener los vectores de desplazamiento y velocidad de un objeto en movimiento, a menudo queremos conocer su vector de aceleración en cualquier punto a lo largo de su trayectoria. Este vector de aceleración es la aceleración instantánea y se puede obtener de la derivada con respecto al tiempo de la función de velocidad, como hemos visto en un capítulo anterior. La única diferencia en dos o tres dimensiones es que estas son ahora cantidades de vectores. Tomando la derivada con respecto al tiempo de $\bold{\vec{v}}(t)$, encontramos
En términos de sus componentes rectangulares
Además, dado que la velocidad es la derivada de la función de posición, podemos escribir la aceleración en términos de la segunda derivada de la función de posición:
Ejemplo 4.5
Encontrando la aceleración de partículas
Una partícula tiene una función de posición $\bold{\vec{r}}(t) = (10t - t^2)\^{\bold{i}} + 5t\^{\bold{j}} + 5t\^{\bold{k}}m$. (a) ¿Cuál es la velocidad? (b) ¿Cuál es la aceleración? (c) Describa el movimiento desde $t = 0 s$.
Estrategia
Podemos obtener una idea del problema mirando la función de posición. Es lineal en $y$ y $z$, por lo que sabemos que la aceleración en estas direcciones es cero cuando tomamos la segunda derivada. Además, ten en cuenta que la posición en la dirección $x$ es cero para $t = 0 s$ y $t = 10 s$.
Solución
(a) Tomando la derivada con respecto al tiempo de la función de posición, encontramos
$$\bold{\vec{v}}(t) = (10 − 2t)\^{\bold{i}} + 5\^{\bold{j}} + 5\^{\bold{k}} m/s$$La función de velocidad es lineal en el tiempo en la dirección $x$ y es constante en las direcciones $y$ y $z$.
(b) Tomando la derivada de la función de velocidad, encontramos
$$\bold{\vec{a}}(t) = −2\^{\bold{i}} m/s^2$$El vector de aceleración es una constante en la dirección $x$ negativa.
(c) La trayectoria de la partícula se puede ver en la Figura 4.9. Miremos las direcciones $y$ y $z$. La posición de la partícula aumenta constantemente como una función del tiempo con una velocidad constante en estas direcciones. En la dirección $x$, sin embargo, la partícula sigue un camino en $x$ positiva hasta $t = 5 s$, cuando invierte la dirección. Lo sabemos al ver la función de velocidad, que se vuelve cero en este momento y negativa a partir de ese momento. También sabemos esto porque la aceleración es negativa y constante, lo que significa que la partícula está desacelerando o acelerando en la dirección negativa. La posición de la partícula alcanza los $25 m$, donde luego invierte la dirección y comienza a acelerar en la dirección $x$ negativa. La posición llega a cero en $t = 10 s$.
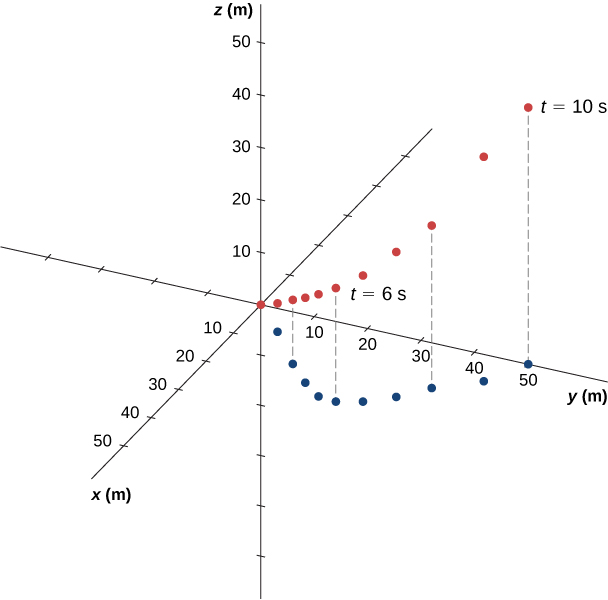
Explicación
Graficando la trayectoria de la partícula, podemos entender mejor su movimiento, dado por los resultados numéricos de las ecuaciones cinemáticas.
 Comprueba tu aprendizaje 4.2
Comprueba tu aprendizaje 4.2
Aceleración constante
El movimiento multidimensional con aceleración constante se puede tratar de la misma manera que se mostró en el capítulo anterior para el movimiento unidimensional. Anteriormente mostramos que el movimiento tridimensional es equivalente a tres movimientos unidimensionales, cada uno a lo largo de un eje perpendicular a los demás. Para desarrollar las ecuaciones relevantes en cada dirección, consideremos el problema bidimensional de una partícula que se mueve en el plano $xy$ con aceleración constante, ignorando el componente $z $por el momento. El vector de aceleración es
$$\bold{\vec{a}} = a_{0x}\^{\bold{i}} + a_{0y}\^{\bold{j}}$$Cada componente del movimiento tiene un conjunto separado de ecuaciones similar a las ecuaciones 3.10 a 3.14 del capítulo anterior sobre el movimiento unidimensional. Mostramos solo las ecuaciones de posición y velocidad en las direcciones $x$ e $y$.
Un conjunto similar de ecuaciones cinemáticas podría escribirse para el movimiento en la dirección $z$:
Aquí el subíndice $0$ denota la posición o velocidad inicial. La ecuación 4.11 a la ecuación 4.18 puede sustituirse en la ecuación 4.2 y la ecuación 4.5 sin el componente $z$ para obtener el vector de posición y el vector de velocidad en función del tiempo en dos dimensiones:
$$\bold{\vec{r}}(t) = x(t)\^{\bold{i}} + y(t)\^{\bold{j}} \text{ y } \bold{\vec{v}}(t) = v_x(t)\^{\bold{i}} + v_y(t)\^{\bold{j}}$$El siguiente ejemplo ilustra un uso práctico de las ecuaciones cinemáticas en dos dimensiones.
Ejemplo 4.6
Un esquiador
La Figura 4.10 muestra un esquiador que se mueve con una aceleración de $2.1 m/s^2$ en una pendiente de $15\degree$ en $t = 0$. Con el origen del sistema de coordenadas en la parte delantera de la cabaña, su posición inicial y velocidad son
$$\bold{\vec{r}}(0) = (75.0\^{\bold{i}} - 50.0\^{\bold{j}}) m$$y
$$\bold{\vec{v}}(0) = (4.1\^{\bold{i}} - 1.1\^{\bold{j}}) m/s$$(a) ¿Cuáles son los componentes $x$ e $y$ de la posición y la velocidad del esquiador como funciones del tiempo? (b) ¿Cuál es su posición y velocidad en $t = 10.0 s$?
Estrategia
Dado que estamos evaluando los componentes de las ecuaciones de movimiento en las direcciones $x$ e $y$, necesitamos encontrar los componentes de la aceleración y ponerlos en las ecuaciones cinemáticas.
Los componentes de la aceleración se encuentran al referirse al sistema de coordenadas en la Figura 4.10. Luego, al insertar las componentes de la posición y velocidad iniciales en las ecuaciones de movimiento, podemos hallar su posición y velocidad en un momento posterior t.
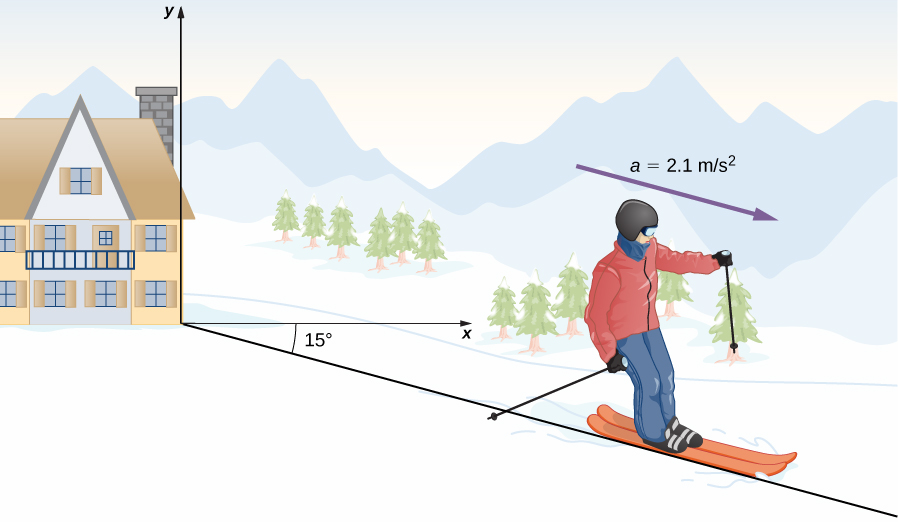
Solución
(a) El origen del sistema de coordenadas está en la cima de la colina con el eje $y$ verticalmente hacia arriba y el eje $x$ horizontal. Al observar la trayectoria del esquiador, el componente $x$ de la aceleración es positivo y el componente y es negativo. Como el ángulo es de $15\degree$ hacia abajo, encontramos
$$a_x = (2.1 m/s^2)cos(15\degree)= 2.0 m/s^2\\ a_y = (-2.1 m/s^2)sen(15\degree)= -0.54 m/s^2$$Al insertar la posición y la velocidad iniciales en la ecuación 4.12 y en la ecuación 4.13 para $x$, tenemos
Para $y$, tenemos
$$y(t) = -50.0 m + (-1.1 m/s)t + \frac12(-0.54 m/s^2)t^2\\ v_y(t) = -1.1 m/s + (-0.54 m/s^2)t$$(b) Ahora que tenemos las ecuaciones de movimiento para $x$ e $y$ como funciones de tiempo, podemos evaluarlas en $t = 10.0 s$:
$$\begin{split} x(10.0s) &= 75.0 m + (4.1 m/s^2)(10.0 s) + \frac12 (2.0 m/s^2)(10.0 s)^2\\ &= 216.0 m \end{split}$$ $$v_x(10.0 s) = 4.1 m/s + (2.0 m/s^2)(10.0 s) = 24.1 m/s$$ $$\begin{split} y(10.0s) &= -50.0 m + (-1.1 m/s^2)(10.0 s) \\ &= +\frac12 (-0.54 m/s^2)(10.0 s)^2 = -88.0 m \end{split}$$ $$v_y(10.0 s) = -1.1 m/s + (-0.54 m/s^2>)(10.0 s) = -6.5 m/s$$La posición y la velocidad en $t = 10.0 s$ son, finalmente,
$$\bold{\vec{r}}(10.0 s) = (216.0\^{\bold{i}} - 88.0\^{\bold{j}}) m\\ \bold{\vec{v}}(10.0 s) = (24.1\^{\bold{i}} - 6.5\^{\bold{j}}) m/s$$La magnitud de la velocidad del esquiador a $10.0 s$ es de $25 m/s$, equivalente a $60 mi/h$.
Explicación
Es útil saber que, dadas las condiciones iniciales de posición, velocidad y aceleración de un objeto, podemos encontrar la posición, la velocidad y la aceleración en cualquier momento posterior.
Con las ecuaciones 4.8 a 4.10, hemos completado el conjunto de expresiones para la posición, la velocidad y la aceleración de un objeto que se mueve en dos o tres dimensiones. Si las trayectorias de los objetos se parecen a las "Flechas rojas" en la imagen de apertura para el capítulo, entonces las expresiones para la posición, la velocidad y la aceleración pueden ser bastante complicadas. En las secciones siguientes, examinamos dos casos especiales de movimiento en dos y tres dimensiones observando el movimiento de proyectil (tiro parabólico) y el movimiento circular.
Movimiento parabólico (Tiro de proyectil)
El movimiento de proyectil es el movimiento de un objeto lanzado o proyectado en el aire, sujeto solo a la aceleración como resultado de la gravedad. Las aplicaciones del movimiento de proyectiles en física e ingeniería son numerosas. Algunos ejemplos incluyen meteoritos cuando entran a la atmósfera de la Tierra, fuegos artificiales y el movimiento de cualquier pelota en los deportes.
Dichos objetos se llaman proyectiles y su ruta se llama trayectoria. El movimiento de los objetos que caen, como se discutió en Movimiento a lo largo de una línea recta, es un tipo de movimiento de proyectil simple y unidimensional en el que no hay movimiento horizontal. En esta sección, consideramos el movimiento de proyectil bidimensional, y nuestro tratamiento no tendrá en cuenta los efectos de la resistencia del aire.
El hecho más importante que hay que recordar aquí es que los movimientos a lo largo de los ejes perpendiculares son independientes y, por lo tanto, se pueden analizar por separado. Discutimos este hecho en los vectores de desplazamiento y velocidad, donde vimos que los movimientos verticales y horizontales son independientes.
La clave para analizar el movimiento del proyectil en dos dimensiones es dividirlo en dos movimientos: uno a lo largo del eje horizontal y el otro a lo largo de la vertical (esta elección de ejes es la más sensata porque la aceleración resultante de la gravedad es vertical, por lo tanto, no hay aceleración a lo largo del eje horizontal cuando la resistencia del aire es insignificante).
Como es habitual, llamamos al eje horizontal el eje $x$ y el vertical al eje $y$. No es necesario que usemos esta elección de ejes; es simplemente conveniente en el caso de la aceleración gravitacional. En otros casos, podemos elegir un conjunto diferente de ejes. La Figura 4.11 ilustra la notación para el desplazamiento, donde definimos $\bold{\vec{s}}$ como el desplazamiento total, y $\bold{\vec{x}}$ e $\bold{\vec{y}}$ son sus vectores componentes a lo largo de los ejes horizontal y vertical, respectivamente. Las magnitudes de estos vectores son $s, x $ e $y$.
Para describir completamente el movimiento del proyectil, debemos incluir la velocidad y la aceleración, así como el desplazamiento. Debemos encontrar sus componentes a lo largo de los ejes $x$ e $y$. Supongamos que todas las fuerzas excepto la gravedad (como la resistencia del aire y la fricción, por ejemplo) son insignificantes. Al definir que la dirección positiva es hacia arriba, los componentes de la aceleración son muy simples:
$$a_y = -g = -9.8 m/s^2 (-32 ft/s^2)$$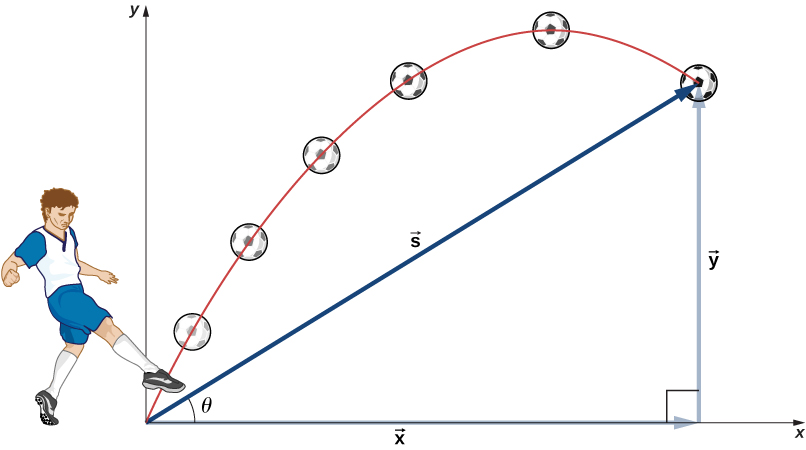
Debido a que la gravedad es vertical, $a_x = 0$. Si $a_x = 0$, significa que la velocidad inicial en la dirección $x$ es igual a la velocidad final en la dirección $x$, o $v_x = v_{0x}$. Con estas condiciones de aceleración y velocidad, podemos escribir la ecuación cinemática 4.11 a través de la ecuación 4.18 para el movimiento en un campo gravitacional uniforme, que incluye el resto de las ecuaciones cinemáticas para una aceleración constante. Las ecuaciones cinemáticas para el movimiento en un campo gravitatorio uniforme se convierten en ecuaciones cinemáticas con $a_y = -g, a_x = 0$:
Movimiento horizontal
Movimiento vertical
Usando este conjunto de ecuaciones, podemos analizar el movimiento del proyectil, teniendo en cuenta algunos puntos importantes.
En el anterior objeto interactivo de PhET Explorations practica, inicialmente, sobre el movimiento de proyectil en términos del ángulo de lanzamiento y la velocidad inicial.
- Halla el movimiento en componentes horizontales y verticales a lo largo de los ejes $x$ e $y$. Las magnitudes de los componentes del desplazamiento $\bold{\vec{s}}$ a lo largo de los ejes son $x$ e $y$. Las magnitudes de las componentes de velocidad $\bold{\vec{v}}$ son $v_x = vcos\theta$ y $v_y = vsen\theta$, donde $v$ es la magnitud de la velocidad y $\theta$ es su dirección relativa a la horizontal, como se muestra en la figura 4.12.
- Considera el movimiento como dos movimientos independientes de una dimensión: uno horizontal y el otro vertical. Usa las ecuaciones cinemáticas para movimiento horizontal y vertical presentadas anteriormente.
- Halla las incógnitas en los dos movimientos separados: uno horizontal y uno vertical. Ten en cuenta que la única variable común entre los movimientos es el tiempo $t$. Los procedimientos de resolución de problemas aquí son los mismos que los de la cinemática unidimensional y se ilustran en los siguientes ejemplos resueltos.
- Combina las cantidades en las direcciones horizontal y vertical para encontrar el desplazamiento total $\bold{\vec{s}}$ y la velocidad $\bold{\vec{v}}$. Halla la magnitud y dirección del desplazamiento y la velocidad usando $$\sqrt{x^2 + y^2}\;\;\; \theta = tan^{-1}(y/x)\;\;\;v = \sqrt{v_x^2 + v_y^2}$$
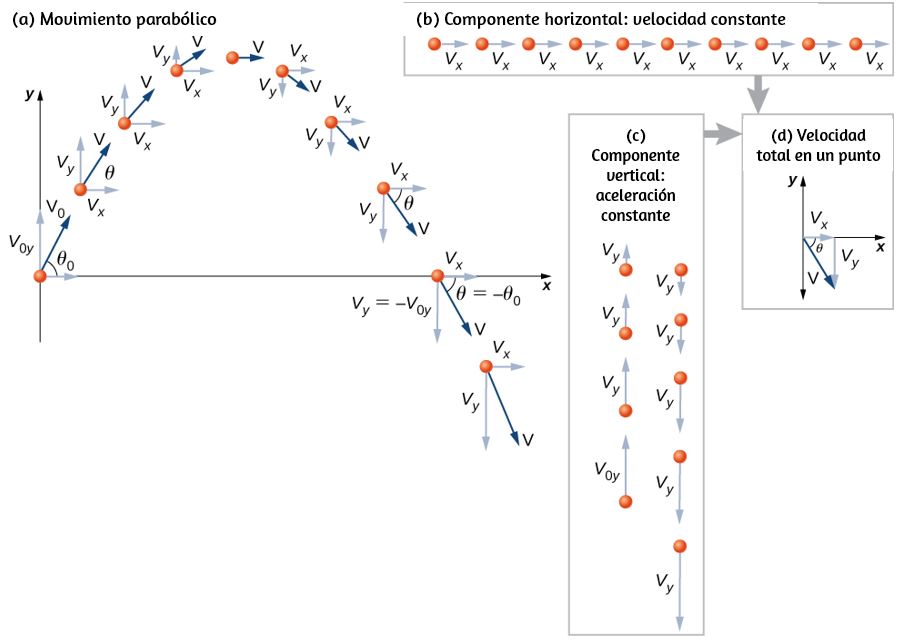
Practica, también, con el interactivo de PhET Explorations, para observar las componentes de velocidad, para ello, selecciona movimiento lento y activa las casillas de los vectores de velocidad
Ejemplo 4.7
Un proyectil de fuegos artificiales estalla alto y lejos
Durante una exhibición de fuegos artificiales, se dispara un proyectil al aire con una velocidad inicial de $70.0 m/s$ en un ángulo de $75.0\degree$ sobre la horizontal, como se ilustra en la figura 4.13. El fusible está programado para encender el caparazón justo cuando alcanza su punto más alto sobre el suelo. (a) Calcule la altura a la que explota el proyectil. (b) ¿Cuánto tiempo pasa entre el lanzamiento del proyectil y la explosión? (c) ¿Cuál es el desplazamiento horizontal del caparazón cuando explota? (d) ¿Cuál es el desplazamiento total desde el punto de lanzamiento hasta el punto más alto?
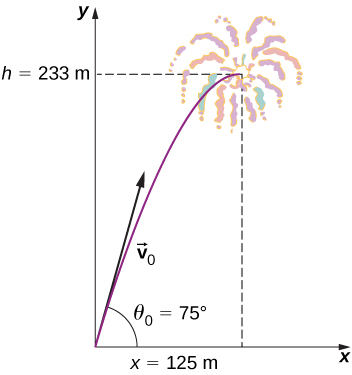
Estrategia
El movimiento se puede dividir en movimientos horizontales y verticales en los que $a_x = 0$ y $a_y = -g$. Entonces podemos definir $x_0$ y $y_0$ como cero y hallar las cantidades deseadas.
Solución
(a) Por "altura" nos referimos a la altitud o posición vertical y por encima del punto de partida. El punto más alto en cualquier trayectoria, llamado ápice, se alcanza cuando $v_y = 0$. Como conocemos las velocidades inicial y final, así como la posición inicial, usamos la siguiente ecuación para encontrar $y$:
$$v_y^2 = v_{0y}^2 - 2g(y - y_0)$$Dado que $y_0$ y $v_y$ valen cero, simplificamos la ecuación así:
$$0 = v_{0y}^2 - 2gy$$Resolviendo para $y$
$$y = \frac{v_{0y}^2}{2g}$$Ahora, debemos encontrar $v_{0y}$, el componente de la velocidad inicial en la dirección $y$. Está dado por $v_{0y} = v_0 sen\theta_0$, donde $v_0$ es la velocidad inicial de $70.0 m/s$ y $\theta_0 = 75\degree$ es el ángulo inicial. Así,
$$v_{0y} = v_0sen\theta = (70.0 m/s)sen 75\degree = 67.6 m/s$$el valor de $y$ es
$$y = \frac{(67.6 m/s)^2}{2(9.80 m/s^2} = 233 m$$Ten en cuenta que como hacia arriba es positivo, la velocidad vertical inicial es positiva, al igual que la altura máxima, pero la aceleración resultante de la gravedad es negativa. Ten en cuenta, también, que la altura máxima depende únicamente de la componente vertical de la velocidad inicial, de modo que cualquier proyectil con una componente vertical inicial de velocidad $67,6 m/s$ alcance una altura máxima de $233 m$ (sin tener en cuenta la resistencia del aire). Los números en este ejemplo son razonables para exhibiciones de fuegos artificiales grandes, cuyos caparazones alcanzan tales alturas antes de explotar. En la práctica, la resistencia del aire no es completamente insignificante, por lo que la velocidad inicial tendría que ser algo mayor que la dada para alcanzar la misma altura.
(b) Como en muchos problemas de física, hay más de una forma de hallar el momento en que el proyectil alcanza su punto más alto. En este caso, el método más fácil es usar $v_y = v_{0y} - gt$. Debido a que $v_y = 0$ en el ápice, esta ecuación se reduce a simplemente
$$0 = v_{0y} - gt$$Despejando y
$$t = \frac{v_{0y}}{g} = \frac{67.6 m/s}{9.80 m/s^2} = 6.90 s$$Esta vez también es razonable para fuegos artificiales grandes.
Si puedes ver el lanzamiento de fuegos artificiales, observa que pasan varios segundos antes de que explote. Otra forma de encontrar el tiempo es mediante $y = y_0 + \frac12 (v_{0y} + v_y)t$. Esto te queda como un ejercicio para comparar.
(c) Debido a que la resistencia del aire es insignificante, $a_x= 0$ y la velocidad horizontal es constante, como se discutió anteriormente. El desplazamiento horizontal es la velocidad horizontal multiplicada por el tiempo dada por $x = x_0 + v_x t$, donde $x_0$ es igual a cero. Así,
$$x = v_x t$$donde $v_x$ es la componente $x$ de la velocidad, la podemos calcular así
$$v_x = v_0 cos\theta = (70.0 m/s)cos75\degree = 18.1m/s$$El tiempo para ambos movimientos es el mismo, para $x$ es
$$x = (18.1 m/s)6.90 s = 125m$$El movimiento horizontal es una velocidad constante en ausencia de resistencia del aire. El desplazamiento horizontal encontrado aquí podría ser útil para evitar que los fragmentos de fuegos artificiales caigan sobre los espectadores. Cuando el proyectil explota, la resistencia del aire tiene un efecto importante, y muchos fragmentos aterrizan directamente debajo.
(d) Las componentes horizontales y verticales del desplazamiento se calcularon, por lo que todo lo que se necesita aquí es encontrar la magnitud y la dirección del desplazamiento en el punto más alto:
Ten en cuenta que el ángulo para el vector de desplazamiento es menor que el ángulo inicial de lanzamiento.
Para ver por qué ocurre esto, revisa la Figura 4.11, que muestra la curvatura de la trayectoria hacia el nivel del suelo.
Al resolver el Ejemplo 4.7(a), la expresión que encontramos para y es válida para cualquier movimiento de proyectil cuando la resistencia del aire es insignificante. Si llamamos a la altura máxima $y = h$. Entonces, $$h = \frac{v_{0y}^2}{2g}$$
Esta ecuación define la altura máxima de un proyectil por encima de su posición de lanzamiento y depende solo de la componente vertical de la velocidad inicial.
En la siguiente escena interactiva, diseñada por Luis Ramírez Vicente, puedes practicar con diferentes valores de velocidad inicial y ángulo del tiro parabólico.
En esa escena, observa las componentes de la velocidad.
 Comprueba tu aprendizaje 4.3
Comprueba tu aprendizaje 4.3
Ejemplo 4.8
Cálculo del movimiento parabólico: tenista
Un tenista gana un partido en el estadio Arthur Ashe y golpea una pelota en las gradas a $30 m/s$ y en un ángulo de $45\degree$ sobre la horizontal (figura 4.14). En su camino hacia abajo, un espectador atrapa la pelota a $10 m$ por encima del punto donde golpeó la pelota. (a) Calcule el tiempo que le toma a la pelota de tenis llegar al espectador. (b) ¿Cuál es la magnitud y dirección de la velocidad de la bola en el impacto?
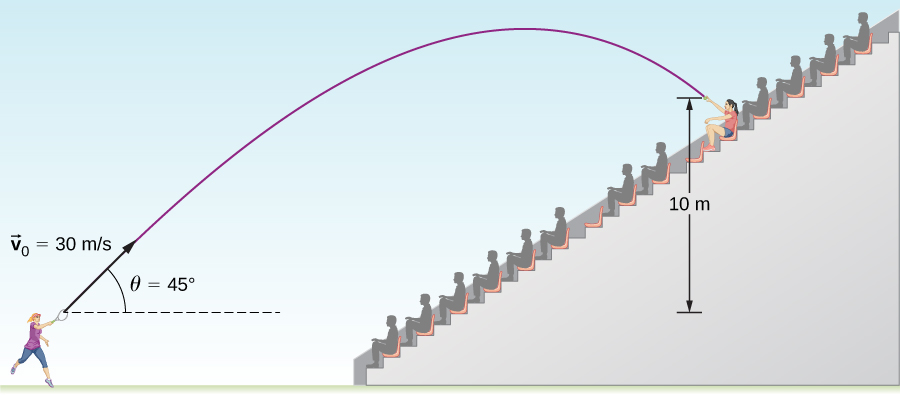
Estrategia
Nuevamente, descomponer este movimiento bidimensional en dos movimientos unidimensionales independientes nos permite hallar las cantidades deseadas.
El tiempo que un proyectil está en el aire se rige solo por su movimiento vertical. Por lo tanto, hallemos $t$ primero. Mientras la bola sube y baja verticalmente, el movimiento horizontal continúa a una velocidad constante. Este ejemplo pregunta por la velocidad final. Por lo tanto, recombinamos los resultados verticales y horizontales para obtener $\bold{\vec{v}}$ en el tiempo final $t$, determinado en la primera parte del ejemplo.
Solución
(a) Mientras la pelota está en el aire, sube y luego cae a una posición final $10.0 m$ más alta que su altitud inicial. Podemos encontrar el tiempo usando la Ecuación 4.22:
$$y = y_0 + v_{0y}t - \frac12 gt^2$$Si tomamos la posición inicial $y_0$ como cero, entonces la posición final es $y = 10 m$. La velocidad vertical inicial es la componente vertical de la velocidad inicial:
$$v_{0y} = v_0 sen\theta_0 = (30.0 m/s)sen 45\degree = 21.2m/s$$Sustituyendo en la ecuación 4.22 por $y$ nos da
$$10.0 m = (21.2 m/s)t - (4.90 m/s^2)t^2$$Al reorganizar los términos obtenemos una ecuación cuadrática en $t$:
$$(4.90 m/s^2)t^2 - (21.2 m/s)t + 10.0 m = 0$$Usando la fórmula cuadrática nos da $t = 3.79 s$ y $t = 0.54 s$.
Como la pelota está a una altura de $10 m$ en dos ocasiones durante su trayectoria, una vez en el camino hacia arriba y otra en el descenso, tomamos la solución más larga durante el tiempo que tarda la pelota en alcanzar al espectador:
$$t = 3.79s$$El tiempo para el movimiento parabólico está determinado completamente por el movimiento vertical. Por lo tanto, cualquier proyectil que tenga una velocidad vertical inicial de $21.2 m/s$ y aterrice $10.0 m$ por debajo de su altitud inicial gasta $3.79 s$ en el aire.
(b) Podemos encontrar las velocidades horizontales y verticales finales $v_x$ y $v_y$ con el uso del resultado de (a). Entonces, podemos combinarlos para encontrar la magnitud del vector de velocidad total $\bold{\vec{v}}$ y el ángulo $\theta$ que forma con la horizontal. Como $v_x$ es constante, podemos resolverlo en cualquier ubicación horizontal. Elegimos el punto de partida porque conocemos tanto la velocidad inicial como el ángulo inicial. Por lo tanto,
$$v_x = v_0cos\theta_0 = (30 m/s)cos45 \degree = 21.2 m/s$$La velocidad vertical final viene dada por la Ecuación 4.21:
$$v_y = v_{0y} - gt$$Como $v_{0y}$ se encontró en la parte (a) en $21,2 m/s$, tenemos
$$v_y = 21.2 m/s − 9.8 m/s^2(3.79 s) = −15.9 m/s$$La magnitud de la velocidad final $\bold{\vec{v}}$ es
$$v = \sqrt{(21.2 m/s)^2 + (-15.9 m/s)^2} = \sqrt{v_x^2 + v_y^2} = 26.5m/s$$La dirección $\theta_v$ se encuentra usando la tangente inversa:
$$\theta_v = tan^{-1}\Big(\frac{v_y}{v_x}\Big) = tan^{-1}\Big(\frac{21.2}{-15.9}\Big) = −53.1\degree$$Explicación
(a) Como se mencionó anteriormente, el tiempo para el movimiento del proyectil está determinado completamente por el movimiento vertical. Por lo tanto, cualquier proyectil que tenga una velocidad vertical inicial de $21.2 m/s$ y aterrice $10.0 m$ por debajo de su altitud inicial gasta $3.79 s$ en el aire. (b) El ángulo negativo significa que el vector de velocidad está $53.1\degree$ por debajo de la horizontal en el punto de impacto. Este resultado es consistente con el hecho de que la pelota está impactando en un punto en el otro lado del ápice de la trayectoria y, por lo tanto, tiene una componente $y$ negativa de la velocidad. La magnitud de la velocidad es menor que la magnitud de la velocidad inicial que esperamos, ya que está impactando $10.0 m$ por encima de la elevación del lanzamiento.
Tiempo de vuelo, trayectoria y rango
De interés son el tiempo de vuelo, la trayectoria y el alcance de un proyectil lanzado sobre una superficie horizontal plana e impactando en la misma superficie. En este caso, las ecuaciones cinemáticas dan expresiones útiles para estas cantidades, que se derivan en las siguientes secciones.
Tiempo de vuelo
Podemos hallar el tiempo de vuelo de un proyectil que se lanza e impacta en una superficie horizontal plana realizando algunas manipulaciones de las ecuaciones cinemáticas. Notamos que la posición y el desplazamiento en y deben ser cero en el lanzamiento y en el impacto en una superficie pareja. Por lo tanto, establecemos el desplazamiento en y igual a cero y encontramos
$$y - y_0 = v_0t - \frac12 gt^2 = (v_0sen\theta_0)t - \frac12 gt^2 = 0$$Factorizando, obtenemos
$$t\Big(v_0sen\theta_0 - \frac{gt}{2}\Big) = 0$$Resolviendo para t
Este es el tiempo de vuelo para un proyectil lanzado e impactando en una superficie horizontal plana. La ecuación 4.24 no se aplica cuando el proyectil aterriza a una altura diferente de la que fue lanzada, como vimos en el ejemplo 4.8 del jugador de tenis golpeando la pelota en las gradas. La otra solución, $t = 0$, corresponde al tiempo de lanzamiento.
El tiempo de vuelo es linealmente proporcional a la velocidad inicial en la dirección $y$, e inversamente proporcional a $g$.
Por lo tanto, en la Luna, donde la gravedad es una sexta parte de la de la Tierra, un proyectil lanzado con la misma velocidad que en la Tierra estaría en el aire seis veces más tiempo.
Trayectoria
La trayectoria de un proyectil se puede encontrar eliminando la variable de tiempo $t$ de las ecuaciones cinemáticas para $t$ arbitraria y resolviendo para $y(x)$. Tomamos $x_0 = y_0 = 0$ para que el proyectil se lance desde el origen. La ecuación cinemática para $x$ da
$$x = v_{0x}t \implies t = \frac{x}{v_{0x}} = \frac{x}{v_0cos\theta_0}$$Sustituyendo esta expresión en la ecuación $y = (v_0sen\theta_0)t − \frac12 gt^2$ obtenemos
$$y = (v_0sen\theta_0) = \Big(\frac{x}{v_0cos\theta_0}\Big) - \frac12 g\Big(\frac{x}{v_0cos\theta_0}\Big)^2$$Reagrupando términos, obtenemos
Esta ecuación de trayectoria es de la forma $y = ax + bx^2$, que es una ecuación de una parábola con coeficientes
$$a = tan\theta_0,\;\;\; b = -\frac{g}{2(v_0cos\theta_0)^2}$$Rango
A partir de la ecuación de la trayectoria también podemos encontrar el rango, o la distancia horizontal recorrida por el proyectil. Factorizando la ecuación 4.25, tenemos
$$y = x\bigg[tan\theta_0 - \frac{g}{2(v_0cos\theta_0)^2}x\bigg]$$La posición $y$ es cero tanto para el punto de lanzamiento como para el punto de impacto, ya que nuevamente estamos considerando solo una superficie horizontal plana. Establecer $y = 0$ en esta ecuación proporciona las soluciones $x = 0$, correspondientes al punto de inicio, y
$$x = \frac{2v_0^2sen\theta_0cos\theta_0}{g}$$correspondiente al punto de impacto. Usando la identidad trigonométrica $2sen\theta cos\theta = sen2\theta$ y asignando $x = R$ para el rango, encontramos
La ecuación 4.26 es válida solo para el lanzamiento y el impacto en una superficie horizontal. El rango es directamente proporcional al cuadrado de la velocidad inicial $v_0$ y $sen2\theta_0$ e inversamente proporcional a la aceleración de la gravedad. Por lo tanto, en la Luna, el rango sería seis veces mayor que en la Tierra para la misma velocidad inicial. Además, vemos desde el factor $sen2\theta_0$ que el rango es máximo a $45\degree$.
Estos resultados se muestran en la figura 4.15 y se pueden verificar en el interactivo. En (a) vemos que cuanto mayor es la velocidad inicial, mayor es el alcance. En (b), vemos que el rango es máximo a $45\degree$. Esto es cierto solo para las condiciones que desprecian la resistencia del aire. Si se considera la resistencia del aire, el ángulo máximo es algo más pequeño. Es interesante que se encuentre el mismo rango para dos ángulos de lanzamiento iniciales que suman $90\degree$. El proyectil lanzado con el ángulo más pequeño tiene un ápice más bajo que el ángulo más alto, pero ambos tienen el mismo rango.
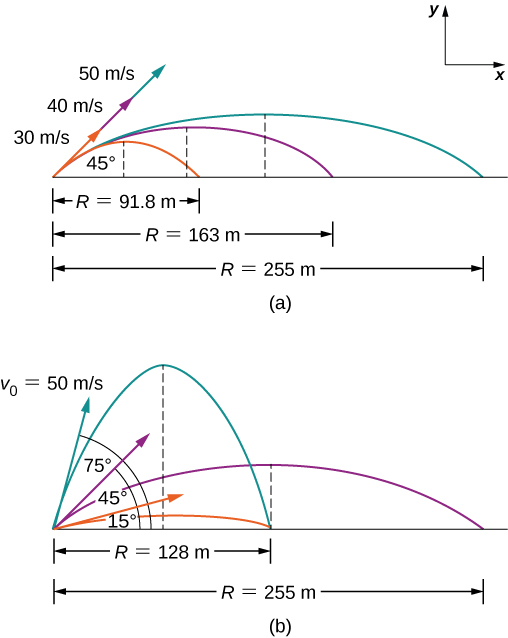
Ejemplo 4.9
Comparando los disparos de golf
Un golfista se encuentra en dos situaciones en diferentes hoyos. En el segundo hoyo está a $120 m$ del green y quiere golpear la bola $90 m$ y dejarla correr hacia el green. Él inclina el tiro hacia el suelo a $30\degree$ con respecto a la horizontal para dejar que la bola ruede después del impacto. En el cuarto hoyo está a $90 m$ del green y quiere dejar caer la pelota con una mínima cantidad de rodadura después del impacto. Aquí, enfoca el tiro a $70\degree$ con respecto a la horizontal para minimizar el balanceo después del impacto. Ambos disparos son golpeados e impactados en una superficie nivelada.
(a) ¿Cuál es la velocidad inicial de la pelota en el segundo hoyo?
(b) ¿Cuál es la velocidad inicial de la pelota en el cuarto hoyo?
(c) Escribe la ecuación de trayectoria para ambos casos.
(d) Grafica las trayectorias.
Estrategia
Vemos que la ecuación del rango tiene la velocidad y el ángulo iniciales, por lo que podemos resolver la velocidad inicial para ambos (a) y (b). Cuando tenemos la velocidad inicial, podemos usar este valor para escribir la ecuación de la trayectoria.
Solución
(a) $R = \frac{v_0^2sen2\theta_0}{g} \implies v_0\sqrt{\frac{Rg}{sen2\theta_0}} = \sqrt{\frac{90.0m(9.8m/s^2)}{sen2(70\degree)}} = 37.0 m/s$
(b) $R = \frac{v_0^2sen2\theta_0}{g} \implies v_0\sqrt{\frac{Rg}{sen2\theta_0}} = \sqrt{\frac{90.0m(9.8m/s^2)}{sen2(30\degree)}} = 31.9 m/s$
(c) $\displaystyle y = x \bigg[tan\theta_0 - \frac{g}{2\big(v_0cos\theta_0\big)^2}x\bigg]$$
Segundo hoyo:
$$\displaystyle y = x\bigg[tan 70\degree - \frac{9.8m/s^2}{2\big[(37.0m/2)(cos70\degree)\big]^2}x\bigg] = 2.75x - 0.0306x^2$$
Cuarto hoyo:
$$\displaystyle y = x\bigg[tan 30\degree - \frac{9.8m/s^2}{2\big[(31.9m/2)(cos30\degree)\big]^2}x\bigg] = 0.58x - 0.0064x^2$$
Explicación
La velocidad inicial del disparo a $70\degree$ es mayor que la velocidad inicial del disparo a $30\degree$. Observa en la figura 4.16 que dos proyectiles lanzados a la misma velocidad pero en diferentes ángulos tienen el mismo alcance si los ángulos de lanzamiento suman $90\degree$. Los ángulos de lanzamiento en este ejemplo se suman para dar un número mayor a $90\degree$. Por lo tanto, el disparo a $70\degree$ tiene que tener una velocidad de lanzamiento mayor para llegar a $90 m$, de lo contrario aterrizaría a una distancia más corta.
 Comprueba tu aprendizaje 4.4
Comprueba tu aprendizaje 4.4
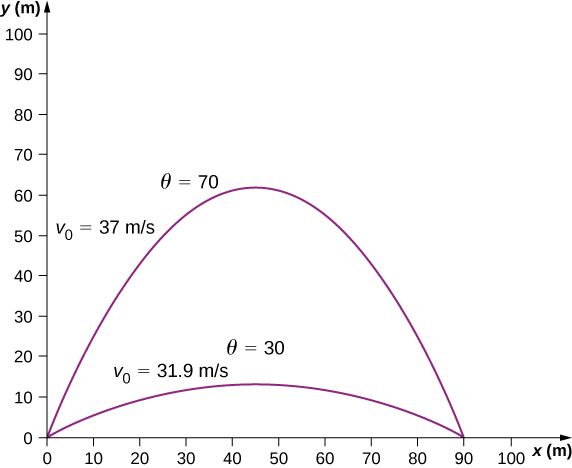
Cuando hablamos del alcance de un proyectil en terreno llano, suponemos que $R$ es muy pequeño en comparación con la circunferencia de la Tierra. Sin embargo, si el alcance es grande, la Tierra se curva debajo del proyectil y la aceleración resultante de la gravedad cambia de dirección a lo largo del camino. El rango es mayor de lo predicho por la ecuación de rango dada anteriormente porque el proyectil tiene más caídas que en terreno nivelado, como se muestra en la figura 4.17, que se basa en un dibujo en los Principia de Newton. Si la velocidad inicial es lo suficientemente grande, el proyectil entra en órbita.
La superficie de la Tierra cae $5 m$ cada $8000 m$. En $1 s$, un objeto cae $5 m$ sin resistencia al aire. Por lo tanto, si a un objeto se le da una velocidad horizontal de $8000 m/s (18,000 mi/h)$ cerca de la superficie de la Tierra, entrará en órbita alrededor del planeta porque la superficie cae continuamente fuera del objeto. Esta es aproximadamente la velocidad del transbordador espacial en una órbita terrestre baja cuando estaba en funcionamiento, o cualquier satélite en una órbita terrestre baja.
Movimiento Circular Uniforme
El movimiento circular uniforme es un tipo específico de movimiento en el que un objeto viaja en círculo con una velocidad constante. Por ejemplo, cualquier punto en una hélice que gira a una velocidad constante está ejecutando un movimiento circular uniforme. Otros ejemplos son las manecillas de segundero, minutero y horario de un reloj. Es notable que los puntos en estos objetos giratorios en realidad están acelerando, aunque la velocidad de rotación es constante. Para ver esto, debemos analizar el movimiento en términos de vectores.
Aceleración centrípeta
En la cinemática unidimensional, los objetos con una velocidad constante tienen aceleración cero. Sin embargo, en la cinemática bidimensional y tridimensional, incluso si la velocidad es constante, una partícula puede tener aceleración si se mueve a lo largo de una trayectoria curva, como un círculo. En este caso, el vector de velocidad está cambiando, o $d\bold{\vec{v}}/dt \ne 0$. Esto se muestra en la figura 4.18. Como la partícula se mueve en sentido antihorario en el tiempo $\Delta t$ en la trayectoria circular, su vector de posición se mueve de $\bold{\vec{r}}(t)$ a $\bold{\vec{r}}(t + \Delta t)$. El vector de velocidad tiene una magnitud constante y es tangente a la ruta, ya que cambia de $\bold{\vec{v}}(t)$ a $\bold{\vec{v}}(t + \Delta t)$, cambiando su dirección solamente. Dado que el vector de velocidad $\bold{\vec{v}}(t) $es perpendicular al vector de posición $\bold{\vec{r}}(t)$, los triángulos formados por los vectores de posición $\Delta\bold{\vec{r}}$, y los vectores de velocidad y $\Delta\bold{\vec{v}}$ son similares. Además, dado que $|\bold{\vec{r}}(t)| = |\bold{\vec{r}}(t + \Delta t)|$ y $|\bold{\vec{v}}(t)| = |\bold{\vec{v}}(t + \Delta t)|$, los dos triángulos son isósceles. A partir de estos hechos, podemos hacer la afirmación
$$\frac{\Delta v}{v} = \frac{\Delta r}{r}\;\;\;\text{o}\;\;\;\Delta v =\frac{v}{r}\Delta r$$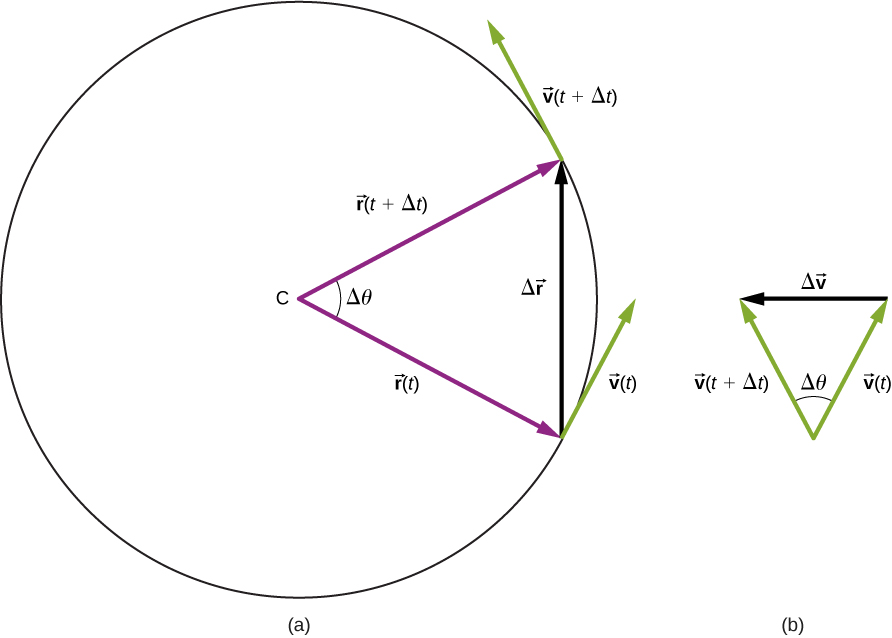
Podemos encontrar la magnitud de la aceleración desde
$$a = \lim\limits_{\Delta t \to 0} \Big(\frac{\Delta v}{\Delta t}\Big) = \frac{v}{r}\Big(\lim\limits_{\Delta t \to 0}\frac{\Delta r}{\Delta t}\Big) = \frac{v^2}{r}$$La dirección de la aceleración también se puede encontrar al observar que cuando $\Delta t$ y, por lo tanto, $\Delta\theta$ se aproximan a cero, el vector $\Delta\bold{\vec{v}}$ se aproxima a una dirección perpendicular a $\bold{\vec{v}}$.
En el límite $\Delta t \to 0$, $\Delta\bold{\vec{v}}$ es perpendicular a $\bold{\vec{v}}$. Como $\bold{\vec{v}}$ es tangente al círculo, la aceleración $d\bold{\vec{v}}/dt$ apunta hacia el centro del círculo.
Resumiendo, una partícula que se mueve en un círculo a una velocidad constante tiene una aceleración con magnitud
La dirección del vector de aceleración está hacia el centro del círculo (Figura 4.19). Esta es una aceleración radial y se llama aceleración centrípeta, por eso le damos el subíndice $c$. La palabra centrípeta proviene de las palabras latinas centrum (que significa "centro") y petere (que significa buscar "), y por lo tanto toma el significado de" búsqueda del centro".
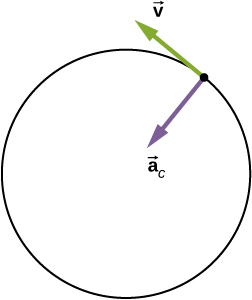
Vamos a investigar algunos ejemplos que ilustran las magnitudes relativas de la velocidad, el radio y la aceleración centrípeta.
Ejemplo 4.10
Creando una aceleración de $1$ g
Un avión a reacción está volando a $134.1 m/s$ a lo largo de una línea recta y gira a lo largo de una trayectoria circular a nivel del suelo. ¿Cuál debes ser el radio del círculo para producir una aceleración centrípeta de $1$ g en el piloto y volar hacia el centro de la trayectoria circular?
Estrategia
Dada la velocidad del jet, podemos hallar el radio del círculo con la expresión de la aceleración centrípeta.
Solución
Establece la aceleración centrípeta igual a la aceleración de la gravedad: $9.8 m/s^2 = \frac{v^2}{r}$
Despejando el radio, encontramos
$$r = \frac{(134.1 m/s)^2}{9.8 m/s^2} = 1835 m = 1.835 km$$Explicación
Para crear una aceleración mayor que $1$ g en el piloto, el chorro tendría que disminuir el radio de su trayectoria circular o aumentar su velocidad en su trayectoria existente o ambas.
 Comprueba tu aprendizaje 4.5
Comprueba tu aprendizaje 4.5
La aceleración centrípeta puede tener un amplio rango de valores, dependiendo de la velocidad y el radio de curvatura de la trayectoria circular. Las aceleraciones centrípetas típicas se dan en la siguiente tabla.
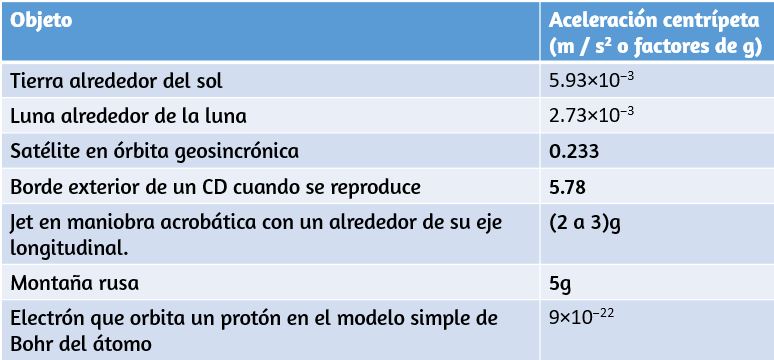
Ecuaciones del movimiento circular uniforme
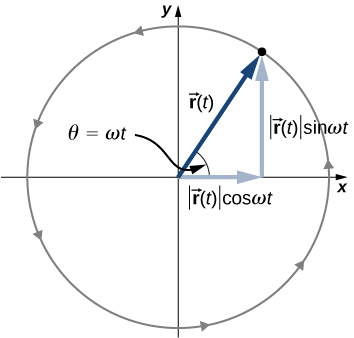
La magnitud del vector de posición es $A = |\bold{\vec{r}}(t)|$ que coincide con el radio del círculo, por lo que en términos de sus componentes,
Aquí, $\omega$ es una constante llamada la frecuencia angular de la partícula. La frecuencia angular tiene unidades de radianes ($rad$) por segundo y es simplemente el número de radianes de medida angular a través del cual pasa la partícula por segundo. El ángulo $\theta$ que el vector de posición tiene en cualquier momento particular es $\omega t$.
Si $T$ es el período de movimiento, o el tiempo para completar una revolución ($2\pi\; rad$), entonces
$$\omega =\frac{2\pi}{T}$$La velocidad y la aceleración se pueden obtener a partir de la función de posición por diferenciación:
De la figura 4.20 se puede demostrar que el vector de velocidad es tangencial al círculo en la ubicación de la partícula, con magnitud $A\omega$. De manera similar, el vector de aceleración se encuentra al diferenciar la velocidad:
De esta ecuación vemos que el vector de aceleración tiene magnitud $A\omega^2$ y se dirige opuesto al vector de posición, hacia el origen, porque $\bold{\vec{a}}(t) = - \omega^2\bold{\vec{r}}(t)$.
Ejemplo 4.11
Movimiento circular de un protón
Un protón tiene una velocidad de $5 \times 10^6 m/s$ y se mueve en un círculo en el plano $xy$ de radio $r = 0.175 m$.
¿Cuál es su posición en el plano $xy$ en el momento $t = 2.0 \times 10^{-7} s = 200 ns$? En $t = 0$, la posición del protón es $0.175 m\^{\bold{i}}$ y gira en sentido antihorario. Dibuja la trayectoria.
Solución
A partir de los datos dados, el protón tiene un período y una frecuencia angular:
$$T = \frac{2\pi r}{v} = \frac{2\pi(0.175 m)}{5 \times 10^6 m/s} = 2.20 \times 10^{-7} s\\ \omega = \frac{2\pi}{T} = 2.856 \times 10^7 rad/s$$La posición de la partícula en $t = 2.0 \times 10^{-7} s$ con $A = 0.175 m$ es
$$\begin{split} \bold{\vec{r}}(2.0 \times 10^{-7} s) &= Acos\omega (2.0 \times 10^{-7} s)\^{\bold{i}} + Asen\omega (2.0 \times 10^{-7} s)\^{\bold{j}} m\\ &= 0.175cos[(2.856\times 10^{7} rad/s)(2.0\times 10^{-7} s)]\^{\bold{i}}\\ & \;\;\;\;\;+ 0.175sen[(2.856\times 10^7 rad/s)(2.0\times 10{-7} s)]\^{\bold{j}}\\ &= 0.175cos(5.712rad)\^{\bold{i}} + 0.175sen(5.712rad)\^{\bold{j}}\\ &= 0.147\^{\bold{i}} + 0.095\^{\bold{j}} m \end{split}$$A partir de este resultado, vemos que el protón se encuentra ligeramente por debajo del eje x. Esto se muestra en la figura 4.21.
Explicación
Escogimos la posición inicial de la partícula para estar en el eje $x$. Esto fue completamente arbitrario. Si se diera una posición inicial diferente, tendríamos una posición final diferente en $t = 200 ns$.
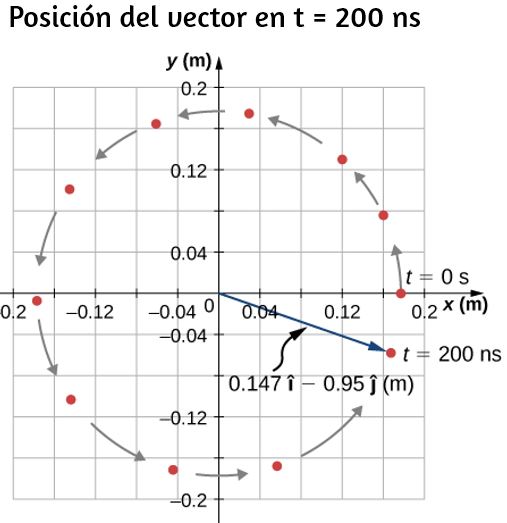
Movimiento circular no uniforme
El movimiento circular no tiene que ser a una velocidad constante. Una partícula puede viajar en un círculo y acelerar o ralentizar, mostrando una aceleración en la dirección del movimiento.
En un movimiento circular uniforme, la partícula que ejecuta el movimiento circular tiene una velocidad constante y el círculo está en un radio fijo. Si la velocidad de la partícula también está cambiando, entonces introducimos una aceleración adicional en la dirección tangencial al círculo.
Tales aceleraciones ocurren en un punto en una parte superior que está cambiando su velocidad de rotación, o cualquier rotor acelerado. En los vectores de desplazamiento y velocidad mostramos que la aceleración centrípeta es la tasa de cambio de tiempo de la dirección del vector de velocidad.
Si la velocidad de la partícula está cambiando, entonces tiene una aceleración tangencial que es la tasa de cambio de tiempo de la magnitud de la velocidad:
La dirección de la aceleración tangencial es tangente al círculo, mientras que la dirección de aceleración centrípeta está radialmente hacia el centro del círculo.
Por lo tanto, una partícula en movimiento circular con una aceleración tangencial tiene una aceleración total que es la suma vectorial de las aceleraciones centrípeta y tangencial:
Los vectores de aceleración se muestran en la figura 4.22. Ten en cuenta que los dos vectores de aceleración $\bold{\vec{a}}_C$ y $\bold{\vec{a}}_T$ son perpendiculares entre sí, con $\bold{\vec{a}}_C$ en la dirección radial y $\bold{\vec{a}}_T$ en la dirección tangencial.
La aceleración total $\bold{\vec{a}}$ apunta en un ángulo entre $\bold{\vec{a}}_C$ y $\bold{\vec{a}}_T$.
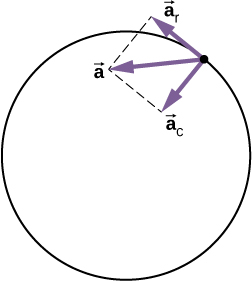
Ejemplo 4.11
Aceleración total durante el movimiento circular
Una partícula se mueve en un círculo de radio $r = 2.0 m$. Durante el intervalo de tiempo desde $t = 1,5 s$ hasta $t = 4,0 s$, su velocidad varía con el tiempo de acuerdo con
$$v(t) = c_1 - \frac{c_2}{t^2}, c_1 = 4.0 m/s, c_2 = 6.0 m\cdot s$$¿Cuál es la aceleración total de la partícula en $t = 2.0 s$?
Estrategia
Se nos da la velocidad de la partícula y el radio del círculo, por lo que podemos calcular la aceleración centrípeta fácilmente. La dirección de la aceleración centrípeta es hacia el centro del círculo.
Encontramos la magnitud de la aceleración tangencial tomando la derivada con respecto al tiempo de $|v(t)|$ usando la ecuación 4.31 y evaluándola en $t = 2.0 s$. Usamos esto y la magnitud de la aceleración centrípeta para encontrar la aceleración total.
Solución
La aceleración centrípeta es
$$v(2.0 s) = \Big(4.0 - \frac{6.0}{(2.0)^2}\Big) m/s = 2.5 m/s$$ $$a_C = \frac{v^2}{r} = \frac{(2.5 m/s)^2}{2.0 m}= 3.1m/s^2$$dirigido hacia el centro del círculo. La aceleración tangencial es
$$a_T = \Big|\frac{d\bold{\vec{v}}}{dt}\Big| = \frac{2c_2}{t^3} = \frac{12.0}{(2.0)^3}m/s^2 = 1.5 m/s^2$$La aceleración total es
$|\bold{\vec{a}}| = \sqrt{3.1^2 + 1.5^2} m/s^2 = 3.44 m/s^2$$
y $\theta = tan^{-1}\frac{3.1}{1.5} = 64\degree$ desde la tangente al círculo. Ver la figura 4.23.
Explicación
Las direcciones de las aceleraciones centrípeta y tangencial se pueden describir más convenientemente en términos de un sistema de coordenadas polares, con vectores unitarios en las direcciones radial y tangencial. Este sistema de coordenadas, que se utiliza para el movimiento a lo largo de trayectorias curvas, se trata en detalle más adelante en el libro.
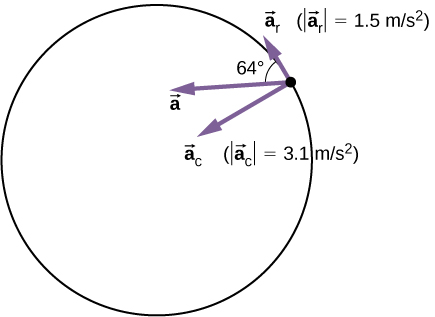
Movimiento relativo en una y dos dimensiones
El movimiento no ocurre de manera aislada. Si viajas en un tren que se mueve a $10 m/s$ al este, esta velocidad se mide en relación con el suelo sobre el que viajas. Sin embargo, si otro tren pasa a $15 m/s$ al este, tu velocidad con respecto a este otro tren es diferente de tu velocidad con respecto al suelo. Tu velocidad con respecto al otro tren es de $5 m/s$ al oeste. Para explorar más esta idea, primero debemos establecer cierta terminología.
Marcos de referencia
Para discutir el movimiento relativo en una o más dimensiones, primero presentamos el concepto de marcos de referencia. Cuando decimos que un objeto tiene una cierta velocidad, debemos decir que tiene una velocidad con respecto a un marco de referencia dado. En la mayoría de los ejemplos que hemos examinado hasta ahora, este marco de referencia ha sido la Tierra.
Si dices que una persona está sentada en un tren que se mueve a $10 m/s$ al este, entonces implica que la persona en el tren se está moviendo con relación a la superficie de la Tierra a esta velocidad, y la Tierra es el marco de referencia. Podemos ampliar nuestra visión del movimiento de la persona en el tren y decir que la Tierra está girando en su órbita alrededor del Sol, en cuyo caso el movimiento se vuelve más complicado.
En este caso, el sistema solar es el marco de referencia. En resumen, toda discusión sobre el movimiento relativo debe definir los marcos de referencia involucrados. Ahora desarrollamos un método para referirnos a los marcos de referencia en movimiento relativo.
Movimiento relativo en una dimensión
Primero introducimos el movimiento relativo en una dimensión, porque los vectores de velocidad se simplifican para tener solo dos direcciones posibles. Toma el ejemplo de la persona sentada en un tren que se mueve hacia el este. Si elegimos este como la dirección positiva y la Tierra como el marco de referencia, entonces podemos escribir la velocidad del tren con respecto a la Tierra como $\bold{\vec{v}}_{TE} = 10 m/s \^{\bold{i}}$ este, donde los subíndices $TE$ se refieren al tren y la tierra, Digamos ahora que la persona se levanta de su asiento y camina hacia la parte posterior del tren a $2 m/s$. Esto nos dice que tiene una velocidad relativa al marco de referencia del tren. Como la persona camina hacia el oeste, en dirección negativa, escribimos su velocidad con respecto al tren como $\bold{\vec{v}}_{PT} = -2 m/s \^{\bold{i}}$. Podemos agregar los dos vectores de velocidad para encontrar la velocidad de la persona con respecto a la Tierra. Esta velocidad relativa se escribe como
$$\bold{\vec{v}}_{PE} = \bold{\vec{v}}_{PT} + \bold{\vec{v}}_{TE}\tag{4.33}$$Ten en cuenta el orden de los subíndices para los diversos marcos de referencia en la ecuación 4.33. Los subíndices para el marco de referencia de acoplamiento, que es el tren, aparecen consecutivamente en el lado derecho de la ecuación. La Figura 4.24 muestra el orden correcto de los subíndices cuando se forma la ecuación del vector.
Sumando los vectores, encontramos $\bold{\vec{v}}_{PE} = 8 m/s \^{\bold{i}}$, por lo que la persona se mueve $8 m/s$ al este con respecto a la Tierra. Gráficamente, esto se muestra en la figura 4.25.
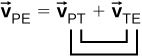

Velocidad relativa en dos dimensiones
Ahora podemos aplicar estos conceptos para describir el movimiento en dos dimensiones. Considera una partícula $P$ y los marcos de referencia $S$ y $S'$,como se muestra en la figura 4.26. La posición del origen de $S'$ medido en $S$ es $\bold{\vec{r}}_{S' S}$, la posición de $P$ medida en $S'$ es $\bold{\vec{r}}_{PS' }$, y la posición de $P$ medida en $S$ es $\bold{\vec{r}}_{PS}$.
De la figura 4.26 vemos que
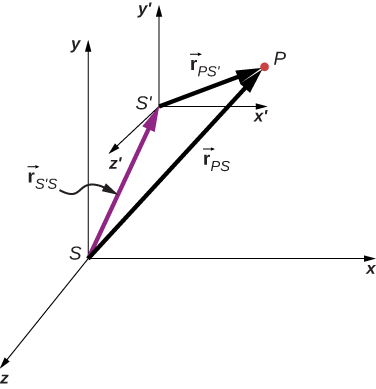
Las velocidades relativas son las derivadas en el tiempo de los vectores de posición. Por lo tanto,
La velocidad de una partícula con respecto a $S$ es igual a su velocidad relativa a $S'$ más la velocidad de $S'$ con respecto a $S$.
Podemos extender la Ecuación 4.35 a cualquier cantidad de marcos de referencia. Para la partícula P con velocidades $\bold{\vec{v}}_{PA}, \bold{\vec{v}}_{PB}$, y $\bold{\vec{v}}_{PC}$ en los marcos de referencia $A, B$ y $C$,
También podemos ver cómo se relacionan las aceleraciones tal como se observa en dos marcos de referencia al diferenciar la Ecuación 4.35:
Vemos que si la velocidad de $S'$ relativa a $S$ es una constante, entonces $\bold{\vec{a}}_{SS'} = 0$ y
Esto dice que la aceleración de una partícula es la misma medida por dos observadores que se mueven a una velocidad constante entre sí.
Movimiento de un automóvil en relación con un camión
Un camión viaja hacia el sur a una velocidad de $70 km/h$ hacia una intersección. Un automóvil está viajando hacia el este hacia la intersección a una velocidad de $80 km/h$ (Figura 4.27). ¿Cuál es la velocidad del automóvil en relación con el camión?
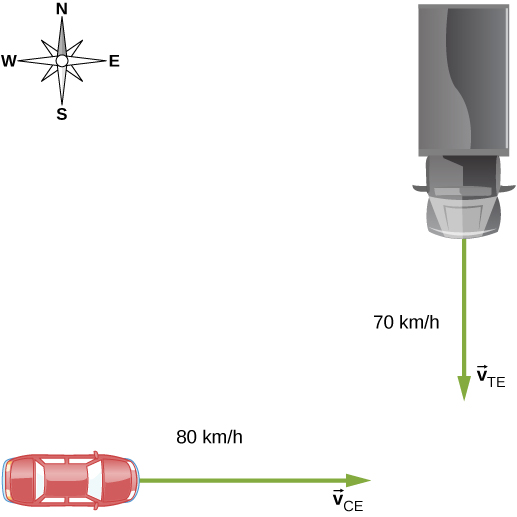
Estrategia
Primero, debemos establecer el marco de referencia común a ambos vehículos, que es la Tierra. Luego, escribimos las velocidades de cada uno con respecto al marco de referencia de la Tierra, lo que nos permite formar una ecuación vectorial que vincula el automóvil, el camión y la Tierra para resolver la velocidad del automóvil con respecto al camión.
Solución
La velocidad del automóvil con respecto a la Tierra es
$\bold{\vec{v}}_{CE} = 80 km/h\^{\bold{i}}$. La velocidad del camión con respecto a la Tierra es $\bold{\vec{v}}_{TE} = -70 km/h\^{\bold{j}}$. Usando la regla de suma de velocidad, la ecuación de movimiento relativo que estamos buscando es
Aquí, $\bold{\vec{v}}_{CT}$ es la velocidad del automóvil con respecto al camión, y la Tierra es el marco de referencia de conexión. Como tenemos la velocidad del camión con respecto a la Tierra, el negativo de este vector es la velocidad de la Tierra con respecto al camión:
$\bold{\vec{v}}_{ET} = -\bold{\vec{v}}_{TE}$. El diagrama vectorial de esta ecuación se muestra en la figura 4.28
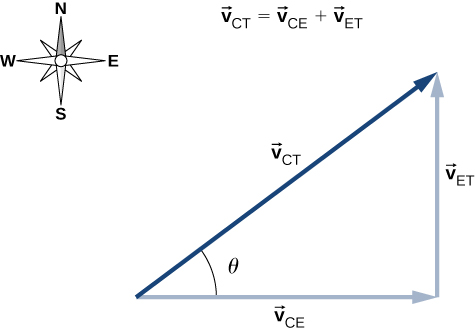
Ahora podemos hallar la velocidad del automóvil con respecto al camión:
$$|\bold{\vec{v}}_{CT}| = \sqrt{(80.0 km/h)^2 + (70.0 km/h)^2} = 106 km/h$$y
$$\theta = tan^{-1}\Big(\frac{70.0}{80.0}\Big) = 41.2\degree\;\;\text{ noreste}$$Explicación
Dibujar un diagrama vectorial que muestre los vectores de velocidad puede ayudar a comprender la velocidad relativa de los dos objetos.
 Comprueba tu aprendizaje 4.6
Comprueba tu aprendizaje 4.6
Ejemplo 4.13
Volar un avión en el viento
Un piloto debe volar su avión hacia el norte para llegar a su destino. El avión puede volar a $300 km/h$ en aire quieto. El viento sopla del noreste a $90 km/h$. (a) ¿Cuál es la velocidad del avión con relación al suelo? (b) ¿En qué dirección debe pilotar el piloto su avión para volar hacia el norte?
Estrategia
El piloto debe apuntar su avión algo al noreste para compensar la velocidad del viento. Necesitamos construir una ecuación vectorial que contenga la velocidad del avión con respecto al suelo, la velocidad del avión con respecto al aire y la velocidad del aire con respecto al suelo. Dado que estas dos últimas cantidades son conocidas, podemos hallar la velocidad del avión con respecto al suelo. Podemos graficar los vectores y usar este diagrama para evaluar la magnitud de la velocidad del avión con respecto al suelo. El diagrama también nos dirá el ángulo que la velocidad del avión tiene con el norte con respecto al aire, que es la dirección en que el piloto debe dirigir su avión.
Solución
La ecuación vectorial es $\bold{\vec{v}}_{PG} = \bold{\vec{v}}_{PA} + \bold{\vec{v}}_{AG}$, donde $P$ = avión, $A$ = aire y $G$ = terreno. A partir de la geometría de la figura 4.29, podemos resolver fácilmente la magnitud de la velocidad del avión con respecto al suelo y el ángulo del rumbo del avión, $\theta$.
(a) Cantidades conocidas:
$$\displaystyle |\bold{\vec{v}}_{PA}| = 300 km/h\;\;\; \text{y}\;\;\; |\bold{\vec{v}}_{AG}| = 90 km/h$$Sustituyendo en la ecuación de movimiento, obtenemos
$|\bold{\vec{v}}_{PG}| = 230 km/h$.
(b) El ángulo $\displaystyle\theta = tan^{-1}\frac{63.64}{300} = 12\degree$ al noreste.
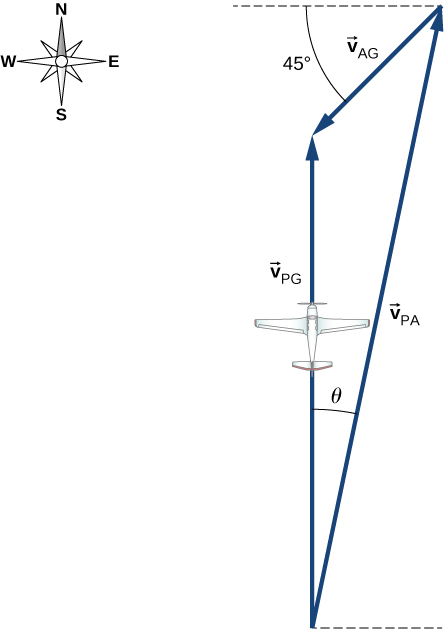
Dinámica: Leyes del
movimiento de Newton
Isaac Newton (Woolsthorpe, 25 de diciembre de 1642 - Londres, 20 de marzo de 1727)
(https://es.wikipedia.org/)
Introducción

Cuando conduces por un puente, esperas que permanezca estable. También esperas acelerar o ralentizar tu automóvil en respuesta a los cambios de tráfico. En ambos casos, lidias con las fuerzas. Las fuerzas en el puente están en equilibrio, por lo que se mantiene en su lugar.
Por el contrario, la fuerza producida por el motor de tu automóvil causa un cambio en el movimiento. Isaac Newton descubrió las leyes del movimiento que describen estas situaciones.
Las fuerzas afectan cada momento de tu vida. Tu cuerpo se mantiene a la fuerza de la Tierra y se mantiene unido por las fuerzas de las partículas cargadas.
Cuando abres una puerta, caminas por una calle, levantas el tenedor o tocas la cara de un bebé, estás aplicando fuerzas. Al enfocar más profundamente, los átomos de tu cuerpo se mantienen unidos por las fuerzas eléctricas, y el núcleo del átomo, llamado núcleo, se mantiene unido por la fuerza más poderosa que conocemos: fuerza nuclear fuerte.
Fuerzas
El estudio del movimiento se denomina cinemática, pero la cinemática solo describe la forma en que se mueven los objetos: su velocidad y su aceleración. La dinámica es el estudio de cómo las fuerzas afectan el movimiento de objetos y sistemas. Considera las causas del movimiento de objetos y sistemas de interés, donde un sistema es algo que se analiza. La base de la dinámica son las leyes de movimiento establecidas por Isaac Newton (1642-1727). Estas leyes proporcionan un ejemplo de la amplitud y simplicidad de los principios bajo los cuales funciona la naturaleza. También son leyes universales en el sentido de que se aplican a situaciones en la Tierra y en el espacio.
Las leyes del movimiento de Newton fueron solo una parte del trabajo monumental que lo ha hecho legendario (Figura 5.2). El desarrollo de las leyes de Newton marca la transición del Renacimiento a la era moderna. Hasta el advenimiento de la física moderna no se descubrió que las leyes de Newton producen una buena descripción del movimiento solo cuando los objetos se mueven a velocidades mucho menores que la velocidad de la luz y cuando esos objetos son más grandes que el tamaño de la mayoría de las moléculas (aproximadamente $10^{-9} m$ de diámetro).
Estas restricciones definen el reino de la mecánica newtoniana. A principios del siglo XX, Albert Einstein (1879-1955) desarrolló la teoría de la relatividad y, junto con muchos otros científicos, la mecánica cuántica.
La mecánica cuántica no tiene las limitaciones presentes en la física newtoniana. Todas las situaciones que consideramos en este capítulo, y todas las anteriores a la introducción de la relatividad, están en el campo de la física newtoniana.

Definición de fuerza de trabajo
La dinámica es el estudio de las fuerzas que hacen que los objetos y los sistemas se muevan. Para entender esto, necesitamos una definición de fuerza de trabajo. Una definición intuitiva de fuerza, es decir, un empujón o un tirón, es un buen lugar para comenzar. Sabemos que un empuje o un tirón tiene tanto magnitud como dirección (por lo tanto, es una cantidad vectorial), por lo que podemos definir la fuerza como el empujar o tirar de un objeto con una magnitud y dirección específicas. La fuerza puede ser representada por vectores o expresada como un múltiplo de una fuerza estándar.
El empujar o tirar de un objeto puede variar considerablemente en magnitud o dirección. Por ejemplo, un cañón ejerce una gran fuerza sobre una bala de cañón que se lanza al aire. Por el contrario, la Tierra ejerce solo una pequeña atracción hacia abajo sobre una pulga. Nuestras experiencias cotidianas también nos dan una buena idea de cómo se suman las fuerzas múltiples. Si dos personas empujan en diferentes direcciones a una tercera persona, como se ilustra en la >Figura 5.3, podríamos esperar que la fuerza total esté en la dirección que se muestra. Como la fuerza es un vector, suma al igual que otros vectores. Las fuerzas, al igual que otros vectores, se representan con flechas y se pueden sumar utilizando el familiar método cabeza a cola o los métodos trigonométricos. Estas ideas fueron desarrolladas en vectores.
La Figura 5.3 (b) es nuestro primer ejemplo de un diagrama de cuerpo libre, que es un esquema que muestra todas las fuerzas externas que actúan sobre un objeto o sistema. El objeto o sistema está representado por un solo punto aislado (o cuerpo libre), y solo se muestran las fuerzas que actúan sobre él que se originan fuera del objeto o sistema, es decir, las fuerzas externas.
Estas fuerzas son las únicas que se muestran porque solo las fuerzas externas que actúan sobre el cuerpo libre afectan su movimiento. Podemos ignorar cualquier fuerza interna dentro del cuerpo. Las fuerzas están representadas por vectores que se extienden hacia afuera desde el cuerpo libre.
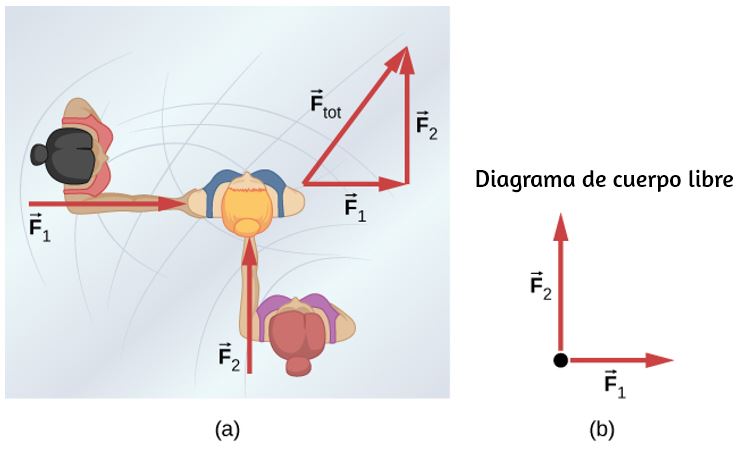
Los diagramas de cuerpo libre son útiles para analizar las fuerzas que actúan sobre un objeto o sistema, y se emplean ampliamente en el estudio y la aplicación de las leyes del movimiento de Newton. Los verás a lo largo de este texto y en todos tus estudios de física. Los siguientes pasos explican brevemente cómo se crea un diagrama de cuerpo libre; examinamos esta estrategia con más detalle en Dibujando Diagramas de Cuerpo Libre.
- Dibuja el objeto bajo consideración. Si estás tratando el objeto como una partícula, representael objeto como un punto. Coloca este punto en el origen de un sistema de coordenadas xy.
- Incluye todas las fuerzas que actúan sobre el objeto, representando estas fuerzas como vectores. Sin embargo, no incluyas la fuerza neta sobre el objeto o las fuerzas que el objeto ejerce en su entorno.
- Descompón todos los vectores de fuerza en componentes x e y.
- Dibuja un diagrama separado de cuerpo libre para cada objeto en el problema.
Ilustramos esta estrategia con dos ejemplos de diagramas de cuerpo libre (Figura 5.4). Los términos utilizados en esta figura se explican con más detalle más adelante en este capítulo.
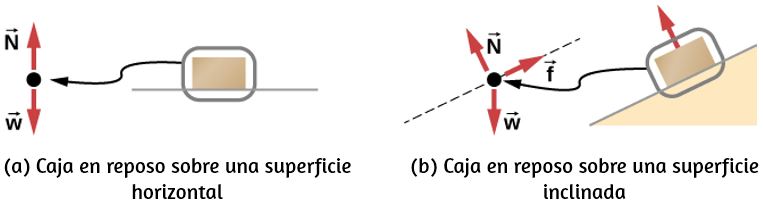
Los pasos son suficientes para guiarte en esta importante estrategia de resolución de problemas. La sección final de este capítulo explica con más detalle cómo dibujar diagramas de cuerpo libre cuando se trabaja con las ideas presentadas en este capítulo.
Desarrollo del concepto de fuerza
Una definición cuantitativa de fuerza puede basarse en alguna fuerza estándar, al igual que la distancia se mide en unidades con respecto a una longitud estándar. Una posibilidad es estirar un resorte a cierta distancia fija (Figura 5.5) y usar la fuerza que ejerce para devolverse, llamada fuerza de restauración, como estándar. La magnitud de todas las demás fuerzas se puede considerar como múltiplos de esta unidad de fuerza estándar. Existen otras posibilidades para las fuerzas estándar. Algunas definiciones alternativas de fuerza se darán más adelante en este capítulo.
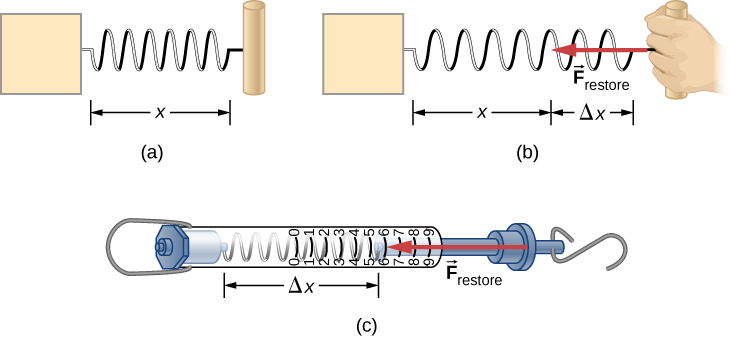
Analicemos la fuerza más profundamente. Supongamos que un estudiante de física se sienta en una mesa, trabajando diligentemente en su tarea (Figura 5.6). ¿Qué fuerzas externas actúan sobre él? ¿Podemos determinar el origen de estas fuerzas?
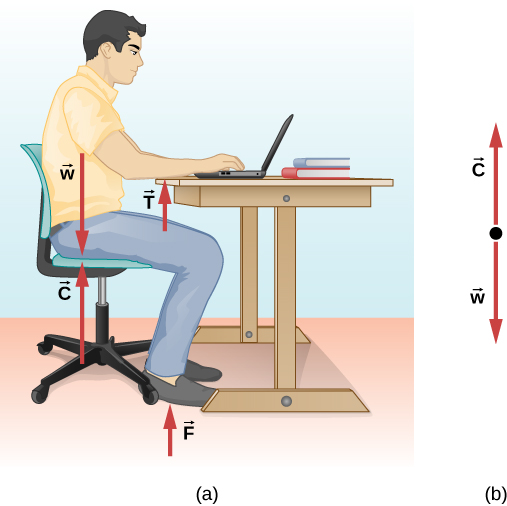
En la mayoría de las situaciones, las fuerzas se agrupan en dos categorías: fuerzas de contacto y fuerzas de campo. Como se puede adivinar, las fuerzas de contacto se deben al contacto físico directo entre los objetos. Por ejemplo, el alumno de la figura 5.6 experimenta las fuerzas de contacto $\bold{\vec{C}}, \bold{\vec{F}}$ y $\bold{\vec{T}}$, que ejerce la silla sobre su parte posterior, el suelo sobre sus pies y la mesa en sus antebrazos, respectivamente. Las fuerzas de campo, sin embargo, actúan sin la necesidad de contacto físico entre los objetos. Dependen de la presencia de un "campo" en la región del espacio que rodea el cuerpo considerado. Como el alumno está en el campo gravitatorio de la Tierra, siente una fuerza gravitatoria $\bold{\vec{w}}$ en otras palabras, él tiene peso.
Puedes pensar en un campo como una propiedad del espacio que es detectable por las fuerzas que ejerce. Los científicos piensan que solo hay cuatro campos de fuerza fundamentales en la naturaleza. Estos son los campos gravitacional, electromagnético, nuclear fuerte y débil (consideramos estas cuatro fuerzas en la naturaleza más adelante en este texto). Como se observa para $\bold{\vec{w}}$ en la Figura 5.6, el campo gravitatorio es responsable del peso de un cuerpo. Las fuerzas del campo electromagnético incluyen las de la electricidad estática y el magnetismo; también son responsables de la atracción entre los átomos en la materia a granel. Tanto los campos de fuerza fuerte como los débiles son efectivos solo a distancias aproximadamente iguales a una longitud de escala no mayor que un núcleo atómico $(10^{-15}m)$. Su rango es tan pequeño que ninguno de los campos tiene influencia en el mundo macroscópico de la mecánica newtoniana.
Las fuerzas de contacto son fundamentalmente electromagnéticas. Mientras que el codo del estudiante en la Figura 5.6 está en contacto con la mesa, las cargas atómicas en su piel interactúan electromagnéticamente con las cargas en la superficie de la mesa.
El resultado neto (total) es la fuerza $\bold{\vec{T}}$. De manera similar, cuando la cinta adhesiva se adhiere a una hoja de papel, los átomos de la cinta se entremezclan con los del papel para generar una fuerza electromagnética neta entre los dos objetos.
Sin embargo, en el contexto de la mecánica newtoniana, el origen electromagnético de las fuerzas de contacto no es una preocupación importante.
Notación vectorial para la fuerza
Como se discutió previamente, la fuerza es un vector; tiene tanto magnitud como dirección. La unidad de fuerza en el SI se llama newton (abreviado $N$), y $1\; N$ es la fuerza necesaria para acelerar un objeto con una masa de $1 \;kg$ a una velocidad de $1 m/s^2$: $1\;N = 1\;kg\cdot m/s^2$. Una manera fácil de recordar el tamaño de un newton es imaginar el sostener una manzana pequeña; tiene un peso de alrededor de $1\;N$.
Podemos describir así una fuerza bidimensional en la forma $\bold{\vec{F}} = a\^{\bold{i}} + b\^{\bold{j}}$ (los vectores unitarios $\^{\bold{i}}$ y $\^{\bold{j}}$ indican la dirección de estas fuerzas a lo largo del eje $x$ y el eje $y$, respectivamente) y una fuerza tridimensional en la forma $\bold{\vec{F}} = a\^{\bold{i}} + b\^{\bold{j}} + c\^{\bold{k}}$. En la Figura 5.3, supongamos que el patinador de hielo $1$, en el lado izquierdo de la figura, empuja horizontalmente con una fuerza de $30.0 N$ hacia la derecha; representamos esto como $\bold{\vec{F}}_1 = 30.0\^{\bold{i}}\; N$. De manera similar, si el patinador de hielo $2 $empuja con una fuerza de $40.0 N$ en la dirección vertical positiva mostrada, escribiríamos $\bold{\vec{F}}_2 = 40.0\^{\bold{j}}\; N$. La resultante de las dos fuerzas hace que se acelere una masa, en este caso, la tercera patinadora sobre hielo.
Esta resultante se denomina fuerza externa neta $\bold{\vec{F}}_{neta}$ y se encuentra tomando la suma vectorial de todas las fuerzas externas que actúan sobre un objeto o sistema (por lo tanto, también podemos representar la fuerza externa neta como $\sum\bold{\vec{F}}$:
Esta ecuación se puede extender a cualquier cantidad de fuerzas.
En este ejemplo, tenemos $\sum\bold{\vec{F}}-{neta} = \sum\bold{\vec{F}}_i = \bold{\vec{F}}_1 + \bold{\vec{F}}_2 = 30.0\^{\bold{i}} + 40.0\^{\bold{j}}\; N$. La hipotenusa del triángulo que se muestra en la Figura 5.3 es la fuerza resultante o fuerza neta. Es un vector. Para encontrar su magnitud (el tamaño del vector, sin importar la dirección), usamos la regla dada en los Vectores, tomando la raíz cuadrada de la suma de los cuadrados de los componentes:
$$\bold{\vec{F}}_{neta} = \sqrt{(30.0 N)^2 + (40.0 N)^2} = 50.0 N$$La dirección está dada por
$$\theta = tan^{−1}\Big(\frac{F_2}{F_1}\Big) = tan^{−1}\Big(\frac{40.0}{30.0}\Big) = 53.1\degree$$medido desde el eje x positivo, como se muestra en el diagrama de cuerpo libre en la figura Figura 5.3 (b).
Supongamos que los patinadores de hielo ahora empujan al tercer patinador de hielo con $\bold{\vec{F}}_1 = 3.0\^{\bold{i}} + 8.0\^{\bold{j}} N$ y $\bold{\vec{F}}_2 = 5.0\^{\bold{i}} + 4.0\^{\bold{j}} N$. ¿Cuál es la resultante de estas dos fuerzas? Debemos reconocer que la fuerza es un vector; por lo tanto, debemos sumar usando las reglas para la suma de vectores:
 Comprueba tu aprendizaje 5.1
Comprueba tu aprendizaje 5.1
En la siguiente escena interactiva, diseñada por Juan Guillermo Rivera Berrío, puedes mover las cabezas de los vectores y verificar la suma de los vectores $\bold{\vec{F}}_1, \bold{\vec{F}}_2$ y $\bold{\vec{F}}_3$, por el método de "cabeza y cola".
Primera Ley de Newton: Ley de inercia
La experiencia sugiere que un objeto en reposo permanece en reposo si se lo deja solo y que un objeto en movimiento tiende a desacelerarse y detenerse a menos que se haga algún esfuerzo para mantenerlo en movimiento. Sin embargo, la primera ley de Newton da una explicación más profunda de esta observación.
Un cuerpo en reposo permanece en reposo o, si está en movimiento, permanece en movimiento a velocidad constante a menos que actúe sobre él una fuerza externa neta.
Ten en cuenta el uso repetido del verbo "permanece". Podemos pensar en esta ley como la preservación del status quo del movimiento. También ten en cuenta la expresión "velocidad constante", esto significa que el objeto mantiene un camino a lo largo de una línea recta, ya que ni la magnitud ni la dirección del vector de velocidad cambia.
Podemos usar la Figura 5.7 para considerar las dos partes de la primera ley de Newton.
En lugar de contradecir nuestra experiencia, la primera ley de Newton dice que debe haber una causa para que ocurra cualquier cambio en la velocidad (un cambio en la magnitud o dirección). Esta causa es una fuerza externa neta, que definimos anteriormente en el capítulo.
Un objeto que se desliza sobre una mesa o piso se desacelera debido a la fuerza neta de fricción que actúa sobre el objeto. Si la fricción desaparece, ¿el objeto aún se ralentizará?

La idea de causa y efecto es crucial para describir con precisión lo que sucede en diversas situaciones. Por ejemplo, considera qué sucede con un objeto deslizándose a lo largo de una superficie horizontal rugosa. El objeto se detiene rápidamente. Si rociamos la superficie con polvos de talco para que la superficie sea más lisa, el objeto se desliza más lejos. Si suavizamos aún más la superficie frotando aceite lubricante sobre ella, el objeto se desliza aún más. Extrapolando a una superficie sin fricción e ignorando la resistencia del aire, podemos imaginar el objeto deslizándose en línea recta indefinidamente. La fricción es, por lo tanto, la causa de la desaceleración (en consonancia con la primera ley de Newton). El objeto no se ralentizaría si se eliminara la fricción.
Considera una mesa de hockey de aire (Figura 5.7). Cuando se apaga el aire, el disco se desliza solo una corta distancia antes de que la fricción lo frene hasta detenerse. Sin embargo, cuando se enciende el aire, crea una superficie casi sin fricción, y el disco se desliza largas distancias sin disminuir la velocidad. Además, si conocemos lo suficiente acerca de la fricción, podemos predecir con precisión qué tan rápido se ralentiza el objeto.
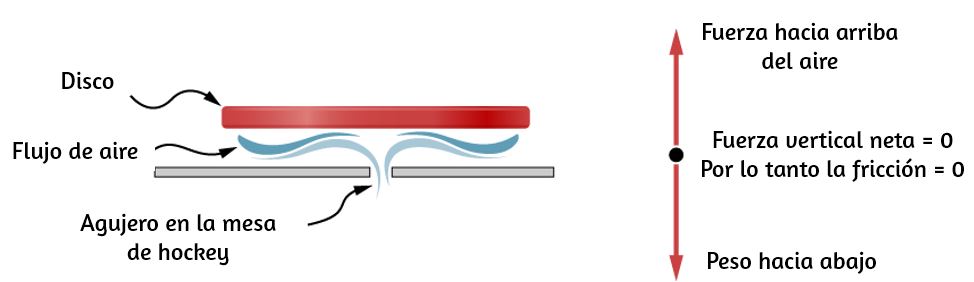
La primera ley de Newton es general y se puede aplicar a cualquier cosa, desde un objeto que se desliza sobre una mesa a un satélite en órbita o a la sangre bombeada desde el corazón. Los experimentos han verificado que cualquier cambio en la velocidad (velocidad o dirección) debe ser causado por una fuerza externa. La idea de leyes generalmente aplicables o universales es importante; es una característica básica de todas las leyes de la física. Identificar estas leyes es como reconocer patrones en la naturaleza de los cuales se pueden descubrir patrones adicionales. El genio de Galileo, quien desarrolló por primera vez la idea de la primera ley del movimiento, y Newton, quien lo aclaró, fue hacer la pregunta fundamental: "¿Cuál es la causa?"
Pensar en términos de causa y efecto es fundamentalmente diferente del enfoque típico griego antiguo, cuando preguntas como "¿Por qué un tigre tiene rayas?" se habría respondido de manera aristotélica, como "Esa es la naturaleza de la bestia". La capacidad de pensar en términos de causa y efecto es la capacidad de establecer una conexión entre un comportamiento observado y el mundo circundante.
Gravitación e inercia
Independientemente de la escala de un objeto, ya sea una molécula o una partícula subatómica, dos propiedades siguen siendo válidas y, por lo tanto, de interés para la física: la gravitación y la inercia. Ambos están conectados a la masa. En general, la masa es una medida de la cantidad de materia en algo. La gravitación es la atracción de una masa a otra, como la atracción entre usted y la Tierra que le mantiene los pies en el suelo. La magnitud de esta atracción es tu peso, y es una fuerza.
La masa también está relacionada con la inercia, la capacidad de un objeto para resistir cambios en su movimiento, en otras palabras, para resistir la aceleración. La primera ley de Newton a menudo se llama ley de inercia. Como sabemos por experiencia, algunos objetos tienen más inercia que otros. Es más difícil cambiar el movimiento de una roca grande que la de una pelota de baloncesto, por ejemplo, porque la roca tiene más masa que la pelota de baloncesto. En otras palabras, la inercia de un objeto se mide por su masa. La relación entre masa y peso se explora más adelante en este capítulo.
Marcos de referencia inerciales
Anteriormente, establecimos la primera ley de Newton como "Un cuerpo en reposo permanece en reposo o, si está en movimiento, permanece en movimiento a velocidad constante a menos que actúe sobre él una fuerza externa neta".
También se puede afirmar que "Todo cuerpo permanece en su estado de movimiento uniforme en línea recta a menos que se vea obligado a cambiar ese estado por fuerzas que actúen sobre él. Para Newton, movimiento uniforme en línea recta significa velocidad constante, que incluye el caso de velocidad cero o reposo. Por lo tanto, la primera ley dice que la velocidad de un objeto permanece constante si la fuerza neta sobre ella es cero.
La primera ley de Newton generalmente se considera como una declaración sobre marcos de referencia. Proporciona un método para identificar un tipo especial de marco de referencia: el marco de referencia inercial. En principio, podemos hacer que la fuerza neta en un cuerpo sea cero. Si su velocidad relativa a un marco dado es constante, entonces ese marco se dice que es inercial. Entonces, por definición, un marco de referencia inercial es un marco de referencia en el que la primera ley de Newton es válida. La primera ley de Newton se aplica a objetos con velocidad constante. A partir de este hecho, podemos inferir la siguiente declaración.
Un marco de referencia que se mueve a velocidad constante con respecto a un marco inercial también es inercial. Un marco de referencia que se acelera con relación a un marco inercial no es inercial.
¿Los marcos inerciales son comunes en la naturaleza? Resulta que dentro del error experimental, un marco de referencia en reposo relativo a las estrellas más distantes o "fijas" es inercial. Todos los marcos que se mueven uniformemente con respecto a este marco de estrella fija también son inerciales. Por ejemplo, un marco de referencia no giratorio unido al Sol es, para todos los propósitos prácticos, inercial, porque su velocidad relativa a las estrellas fijas no varía en más de una parte de $10^{10}$.
La Tierra acelera en relación con las estrellas fijas porque gira sobre su eje y gira alrededor del Sol; por lo tanto, un marco de referencia unido a su superficie no es inercial. Para la mayoría de los problemas, sin embargo, dicho marco sirve como una aproximación suficientemente precisa para un marco inercial, porque la aceleración de un punto en la superficie de la Tierra con respecto a las estrellas fijas es bastante pequeña ($\lt 3.4 \times 10^{-2} m/s^2 $). Por lo tanto, a menos que se indique lo contrario, consideramos que los marcos de referencia fijados en la Tierra son inerciales.
Finalmente, ningún marco inercial particular es más especial que cualquier otro. En lo que respecta a las leyes de la naturaleza, todos los marcos inerciales son equivalentes. Al analizar un problema, elegimos un marco inercial sobre otro simplemente por conveniencia.
La Primera Ley y el Equilibrio de Newton
La primera ley de Newton nos dice sobre el equilibrio de un sistema, que es el estado en el cual las fuerzas en el sistema están equilibradas. Volviendo a las Fuerzas y los patinadores sobre hielo en la Figura 5.3, sabemos que las fuerzas $\bold{\vec{F}}_1$ y $\bold{\vec{F}}_2$ se combinan para formar una fuerza resultante, o la fuerza externa neta: $\bold{\vec{F}}_R = \bold{\vec{F}}_{Neta} = \bold{\vec{F}}_1 + \bold{\vec{F}}_2$. Para crear equilibrio, necesitamos una fuerza equilibradora que produzca una fuerza neta de cero. Esta fuerza debe ser igual en magnitud pero opuesta en dirección a $\bold{\vec{F}}_R$, lo que significa que el vector debe ser $-\bold{\vec{F}}_R$. En referencia a los patinadores sobre hielo, para los cuales encontramos que $\bold{\vec{F}}_R$ es $30.0\^{\bold{i}} + 40.0\^{\bold{j}} N$, podemos determinar la fuerza de equilibrio simplemente encontrando $-\bold{\vec{F}}_R = -30.0\^{\bold{i}} - 40.0\^{\bold{j}} N$. Ver el diagrama de cuerpo libre en la Figura 5.3 (b).
Podemos dar la primera ley de Newton en forma vectorial:
Esta ecuación dice que una fuerza neta de cero implica que la velocidad $\bold{\vec{v}}$ del objeto es constante (la palabra "constante" puede indicar velocidad cero).
La primera ley de Newton es engañosamente simple. Si un automóvil está en reposo, las únicas fuerzas que actúan sobre él son el peso y la fuerza de contacto del pavimento que empuja hacia arriba el automóvil (Figura 5.3). Es fácil entender que se requiere una fuerza neta no nula para cambiar el estado de movimiento del automóvil. Sin embargo, si el automóvil está en movimiento con velocidad constante, una idea errónea común es que la fuerza del motor que impulsa el automóvil hacia delante es de mayor magnitud que la fuerza de fricción que se opone al movimiento hacia adelante. De hecho, las dos fuerzas tienen la misma magnitud.
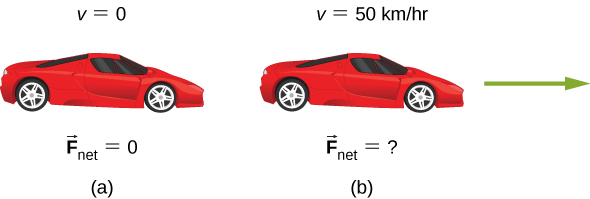
Ejemplo 5.1
¿Cuándo se aplica la primera ley de Newton a tu automóvil?
Las leyes de Newton se pueden aplicar a todos los procesos físicos que involucran fuerza y movimiento, incluyendo algo tan mundano como conducir un automóvil.
- Tu auto está estacionado afuera de tu casa. ¿Se aplica la primera ley de Newton en esta situación? ¿Por qué o por qué no?
- Tu auto se mueve a velocidad constante por la calle. ¿Se aplica la primera ley de Newton en esta situación? ¿Por qué o por qué no?
Estrategia
En (a), estamos considerando la primera parte de la primera ley de Newton, que trata de un cuerpo en reposo; en (b), nos fijamos en la segunda parte de la primera ley de Newton para un cuerpo en movimiento.
Solución
Cuando tu automóvil está estacionado, todas las fuerzas en el automóvil deben estar equilibradas; la suma del vector es $0 \;N$. Por lo tanto, la fuerza neta es cero, y se aplica la primera ley de Newton. La aceleración del automóvil es cero, y en este caso, la velocidad también es cero.
Cuando tu automóvil se mueve a velocidad constante por la calle, la fuerza neta también debe ser cero según la primera ley de Newton.
El motor del automóvil produce una fuerza hacia delante; la fricción, una fuerza entre la carretera y los neumáticos del automóvil que se opone al movimiento hacia adelante, tiene exactamente la misma magnitud que la fuerza del motor, produciendo la fuerza neta de cero.
El cuerpo continúa en su estado de velocidad constante hasta que la fuerza neta se vuelve distinta de cero. Ten en cuenta que una fuerza neta de cero significa que un objeto está en reposo o moviéndose a velocidad constante, es decir, no está acelerando. ¿Qué supones que sucede cuando el automóvil acelera? Exploramos esta idea en la siguiente sección.
Explicación
Como muestra este ejemplo, hay dos tipos de equilibrio. En (a), el automóvil está en reposo; decimos que está en equilibrio estático. En (b), las fuerzas en el automóvil están equilibradas, pero el automóvil se está moviendo; decimos que está en equilibrio dinámico. (Examinamos esta idea con más detalle en Equilibrio estático y Elasticidad). De nuevo, es posible que dos (o más) fuerzas actúen sobre un objeto para que el objeto se mueva. Además, una fuerza neta de cero no puede producir aceleración.
En el siguiente objeto interactivo, diseñado por Carlos Alberto Jaimes Vergara, se recrea el experimento de Galileo quién ya había advertido que en ausencia de fricción, un cuerpo no requiere una fuerza para mantener el estado de movimiento rectilíneo uniforme. Lo anterior se cumple a través de la manipulación de variables de interés como la inclinación de la segunda rampa, que lleva al móvil a recorrer mayor distancia conforme dicha inclinación disminuye; hasta que, cuando la pendiente tiene un valor de cero, es decir, queda totalmente horizontal, el móvil continúa indefinidamente en movimiento rectilíneo uniforme, asumiendo siempre que no hay fricción.
 Comprueba tu aprendizaje 5.2
Comprueba tu aprendizaje 5.2
Experimento de GalileoPara plantear su primera ley del movimiento, Newton se apoyó en las ideas y el trabajo de Galileo y René Descartes (1596-1659). Galileo había experimentado con planos inclinados para establecer el llamado “principio de inercia”, mientras que Descartes había llegado a él a través de la especulación (http://www.cursosinea.conevyt.org.mx).
Segunda Ley de Newton
La segunda ley de Newton está estrechamente relacionada con la primera. Matemáticamente da la relación de causa y efecto entre la fuerza y los cambios en el movimiento. La segunda ley de Newton es cuantitativa y se usa ampliamente para calcular lo que sucede en situaciones que involucran una fuerza. Antes de escribir la segunda ley de Newton como una ecuación simple que da la relación exacta de fuerza, masa y aceleración, debemos afinar algunas ideas que mencionamos anteriormente.
Fuerza y aceleración
Primero, ¿qué queremos decir con un cambio de movimiento? La respuesta es que un cambio de movimiento es equivalente a un cambio en la velocidad. Un cambio en la velocidad significa, por definición, que hay aceleración. La primera ley de Newton dice que una fuerza externa neta causa un cambio en el movimiento; por lo tanto, vemos que una fuerza externa neta causa una aceleración distinta de cero.
Hemos definido fuerza externa como una fuerza que actúa sobre un objeto o sistema que se origina fuera del objeto o sistema. Una noción intuitiva de externo es aquello que está fuera del sistema de interés. Por ejemplo, en la Figura 5.10(a), el sistema de interés es el automóvil más la persona dentro de él. Las dos fuerzas ejercidas por los dos estudiantes son fuerzas externas. Por el contrario, la fuerza que la persona en el automóvil ejerce para aferrarse al volante es una fuerza interna entre los elementos del sistema de interés. Solo las fuerzas externas afectan el movimiento de un sistema, de acuerdo con la primera ley de Newton. (Las fuerzas internas se anulan mutuamente, como se explica en la siguiente sección). A veces, el sistema es obvio, mientras que en otros momentos, identificar sus límites es más sutil.
El concepto de un sistema es fundamental para muchas áreas de la física, como lo es la correcta aplicación de las leyes de Newton.
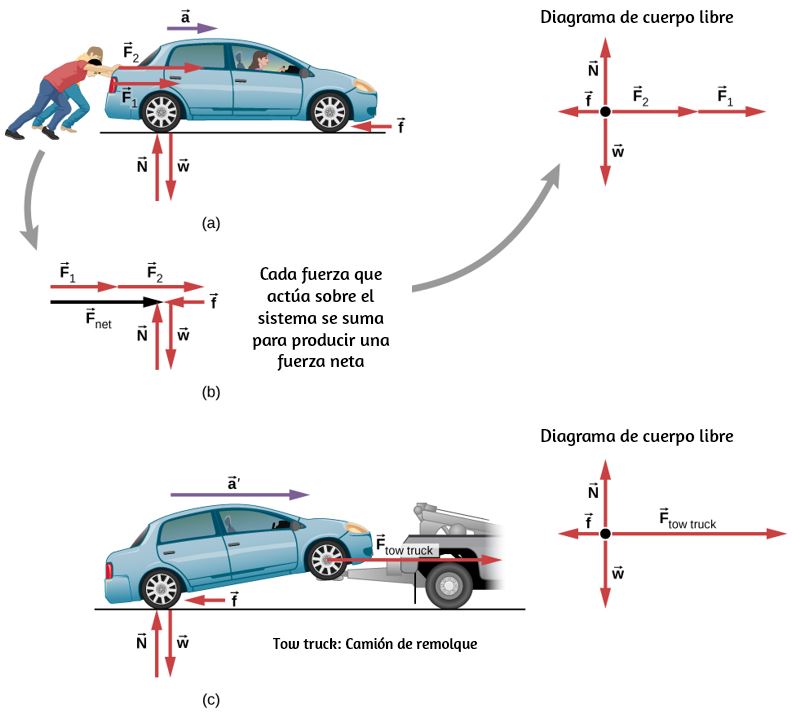
A partir de este ejemplo, puedes ver que las diferentes fuerzas ejercidas sobre la misma masa producen diferentes aceleraciones.
En la Figura 5.10(a), los dos estudiantes empujan un automóvil con un conductor. Se muestran flechas que representan todas las fuerzas externas. El sistema de interés es el automóvil y su conductor. El peso $\bold{\vec{w}}$ del sistema y el soporte del suelo $\bold{\vec{N}}$ también se muestran, se supone que se cancelan (porque no hubo movimiento vertical ni desequilibrio de fuerzas en la dirección vertical para crear un cambio en el movimiento) . El vector $\bold{\vec{f}}$ representa la fricción que actúa sobre el automóvil, y actúa a la izquierda, oponiéndose al movimiento del automóvil. (Discutimos la fricción con más detalle en el siguiente capítulo). En la Figura 5.10(b), todas las fuerzas externas que actúan en el sistema se suman para producir la fuerza neta $\bold{\vec{v}}_{Neta}$. El diagrama de cuerpo libre muestra todas las fuerzas que actúan sobre el sistema de interés. El punto representa el centro de masa del sistema. Cada vector de fuerza se extiende desde este punto. Debido a que hay dos fuerzas que actúan a la derecha, los vectores se muestran colinealmente. Finalmente, en la Figura 5.10(c), una fuerza externa neta mayor produce una mayor aceleración ($\bold{\vec{a'}} \gt \bold{\vec{a}}$) cuando la grúa tira del automóvil.
Parece razonable que la aceleración sea directamente proporcional y en la misma dirección que la fuerza externa neta que actúa sobre un sistema. Esta suposición se ha verificado experimentalmente y se ilustra en la Figura 5.10. Para obtener una ecuación para la segunda ley de Newton, primero escribimos la relación de aceleración $\bold{\vec{a}}$ y la fuerza externa neta $\bold{\vec{v}}_{Neta}$ como la proporcionalidad,
$$\bold{\vec{a}} \propto \bold{\vec{v}}{_Neta}$$donde el símbolo $\propto$ significa "proporcional a." (recuerda que la fuerza externa neta es la suma de todas las fuerzas externas y a veces se indica como $\sum\bold{\vec{F}}$).
Esta proporcionalidad muestra lo que hemos dicho en palabras -acceleración es directamente proporcional a la fuerza externa neta-. Una vez que se elige el sistema de interés, identifica las fuerzas externas e ignora las internas. Es una tremenda simplificación ignorar las numerosas fuerzas internas que actúan entre los objetos dentro del sistema, como las fuerzas musculares dentro de los cuerpos de los estudiantes, y mucho menos la miríada de fuerzas entre los átomos en los objetos. Aún así, esta simplificación nos ayuda a resolver algunos problemas complejos.
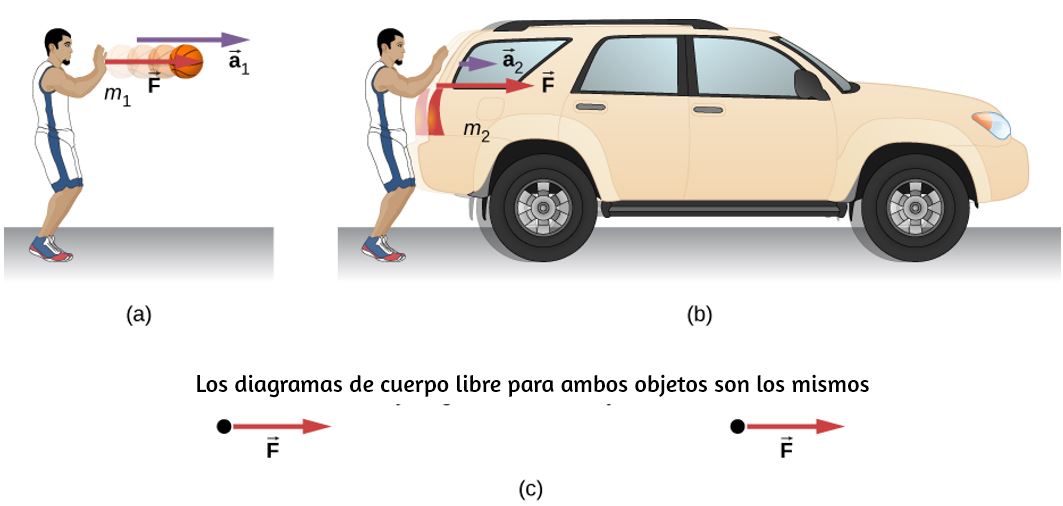
También parece razonable que la aceleración sea inversamente proporcional a la masa del sistema. En otras palabras, cuanto mayor es la masa (la inercia), menor es la aceleración producida por una fuerza dada.
Como se ilustra en la Figura 5.11, la misma fuerza externa neta aplicada a una pelota de baloncesto produce una aceleración mucho menor cuando se aplica a una SUV. La proporcionalidad se escribe como
$$\alpha \propto \frac{1}{m}$$donde $m$ es la masa del sistema y $a$ es la magnitud de la aceleración. Los experimentos han demostrado que la aceleración es exactamente inversamente proporcional a la masa, así como es directamente proporcional a la fuerza externa neta.
Se ha encontrado que la aceleración de un objeto depende solo de la fuerza externa neta y la masa del objeto. La combinación de las dos proporcionalidades dadas genera la segunda ley de Newton.
La aceleración de un sistema es directamente proporcional y en la misma dirección que la fuerza externa neta que actúa en el sistema y es inversamente proporcional a su masa. En forma de ecuación, la segunda ley de Newton es $$\bold{\vec{a}} = \frac{\bold{\vec{v}}_{Neta}}{m}$$ donde $\bold{\vec{a}}$ es la aceleración, $\bold{\vec{v}}_{Neta}$ es la fuerza neta, y $m$ es la masa. Esto a menudo se escribe en la forma más familiar $$\bold{\vec{F}}_{Neta} = \sum\bold{\vec{F}} = \sum\bold{\vec{F}} = m\bold{\vec{a}}\tag{5.3}$$
$$\bold{\vec{F}}_{Neta} = ma\tag{5.4}$$
La ley es una relación de causa y efecto entre tres cantidades que no se basa simplemente en sus definiciones. La validez de la segunda ley se basa en la verificación experimental. El diagrama de cuerpo libre, que aprenderás a dibujar en un próximo apartado, es la base para escribir la segunda ley de Newton.
Ejemplo 5.2
¿Qué aceleración puede producir una persona al empujar una cortadora de césped?
Supongamos que la fuerza externa neta (empuje menos fricción) ejercida sobre una cortadora de césped es $51 N$ (aproximadamente $11 lb$) paralela al suelo (Figura 5.12). La masa de la podadora es de 24 kg. ¿Cuál es su aceleración?
p>EstrategiaEste problema involucra solo movimiento en la dirección horizontal; también se nos da la fuerza neta, indicada por el vector único, pero podemos suprimir la naturaleza vectorial y concentrarnos en aplicar la segunda ley de Newton. Como se dan $\bold{\vec{F}}_{Neta}$ y $m$, la aceleración puede calcularse directamente a partir de la segunda ley de Newton como $\bold{\vec{F}}_{Neta} = ma$.
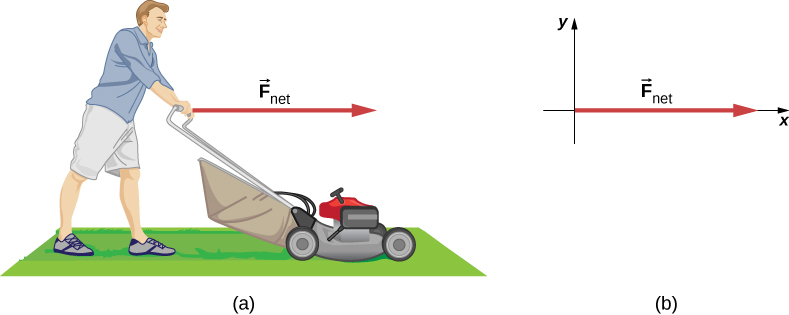
Solución
La magnitud de la aceleración $a$ es $a = F_{Neta}/ma$. Al reemplazar con los valores conocidos obtenemos
$$a = \frac{51 N}{24 kg}$$Convirtiendo la unidades de newtons a kilogramos por metros por segundo cuadrado,
$$a = \frac{51 kg\cdot m/s^2}{24 kg} = 2.1 m/s^2$$La dirección de la aceleración es la misma dirección que la de la fuerza neta, que es paralela al suelo. Esto es el resultado de la relación vectorial expresada en la segunda ley de Newton, es decir, el vector que representa la fuerza neta es el múltiplo escalar del vector de aceleración.
No hay información dada en este ejemplo sobre las fuerzas externas individuales que actúan en el sistema, pero podemos decir algo sobre sus magnitudes relativas. Por ejemplo, la fuerza ejercida por la persona que empuja el cortacésped debe ser mayor que la fricción que se opone al movimiento (ya que sabemos que el cortacésped se movió hacia adelante) y las fuerzas verticales deben cancelarse porque no hay aceleración en la dirección vertical (el cortacésped se mueve solo horizontalmente). La aceleración encontrada es lo suficientemente pequeña lo que es razonable para una persona que empuja una cortadora de césped. Tal esfuerzo no duraría demasiado, porque pronto se alcanzaría la velocidad máxima de la persona.
 Comprueba tu aprendizaje 5.3
Comprueba tu aprendizaje 5.3
En el ejemplo anterior, tratamos con la fuerza neta solo por simplicidad. Sin embargo, varias fuerzas actúan sobre la cortadora de césped. El peso $\bold{\vec{w}}$ (que se discutirá en detalle en Masa y Peso) tira hacia abajo del cortacésped, hacia el centro de la Tierra; esto produce una fuerza de contacto en el suelo. El suelo debe ejercer una fuerza ascendente sobre el cortacésped, conocida como la fuerza normal $\bold{\vec{N}}$, que definiremos en el apartado de las Fuerzas Comunes. Estas fuerzas están balanceadas y por lo tanto no producen aceleración vertical. En el siguiente ejemplo, mostramos ambas fuerzas. A medida que continúes resolviendo problemas usando la segunda ley de Newton, asegúrate de mostrar múltiples fuerzas.
Ejemplo 5.3
¿Qué fuerza es más grande?
(a) El automóvil que se muestra en la Figura 5.13 se mueve a una velocidad constante. ¿Qué fuerza es más grande, $\bold{\vec{F}}_{motor}$ o $\bold{\vec{F}}_{fricción}$? Explica.
(b) El mismo automóvil ahora se está acelerando hacia la derecha. ¿Qué fuerza es más grande, $\bold{\vec{F}}_{motor}$ o $\bold{\vec{F}}_{fricción}$? Explica.
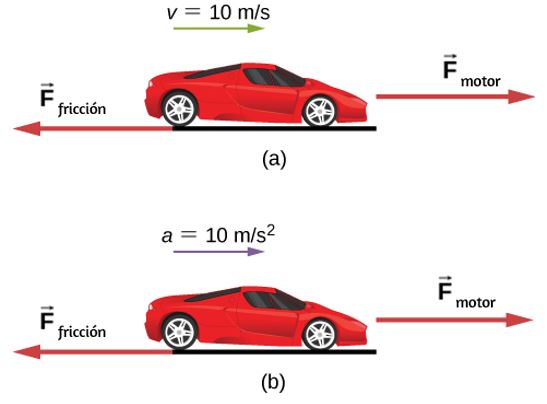
Estrategia
Debemos considerar la primera y la segunda ley de Newton para analizar la situación. Necesitamos decidir qué ley aplica; esto, a su vez, nos dirá acerca de la relación entre las fuerzas.
Solución
a. Las fuerzas son iguales. De acuerdo con la primera ley de Newton, si la fuerza neta es cero, la velocidad es constante.
b. En este caso, $\bold{\vec{F}}{motor}$ debe ser mayor que $\bold{\vec{F}}{}$. Según la segunda ley de Newton, se requiere una fuerza neta para causar aceleración.
Explicación
Estas preguntas pueden parecer triviales, pero comúnmente se responden incorrectamente. Para que un automóvil o cualquier otro objeto se mueva, debe acelerarse desde el descanso hasta la velocidad deseada; esto requiere que la fuerza del motor sea mayor que la fuerza de fricción. Una vez que el automóvil se mueve a una velocidad constante, la fuerza neta debe ser cero; de lo contrario, el automóvil acelerará (gana velocidad).
Para resolver problemas relacionados con las leyes de Newton, debemos entender si aplicamos la primera ley de Newton (donde $\sum\bold{\vec{F}} = 0$) o la segunda ley de Newton (donde $\sum\bold{\vec{F}}$ no es cero). Esto será evidente a medida que veas más ejemplos e intentes resolver problemas por tu cuenta.
Ejemplo 5.4
¿Qué empuje de cohete acelera este trineo?
Antes de los vuelos espaciales tripulados, los trineos cohete se usaban para probar aeronaves, equipos de misiles y efectos fisiológicos en sujetos humanos a altas velocidades. Consistieron en una plataforma que fue montada en uno o dos carriles y propulsada por varios cohetes.
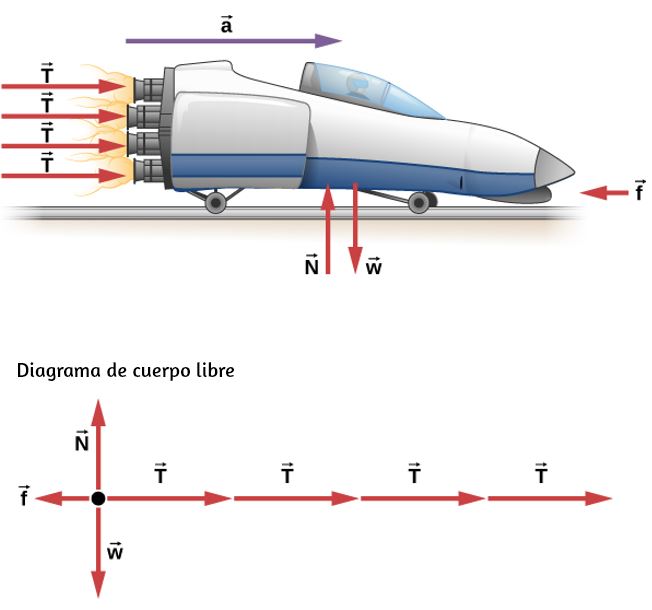
Calcula la magnitud de la fuerza ejercida por cada cohete, llamada empuje $T$, para el sistema de propulsión de cuatro cohetes que se muestra en la Figura 5.14. La aceleración inicial del trineo es de $49 m/s^2$, la masa del sistema es de $2100 kg$ y la fuerza de fricción que se opone al movimiento es de $650 N$.
Estrategia
Aunque las fuerzas actúan tanto vertical como horizontalmente, asumimos que las fuerzas verticales se cancelan porque no hay aceleración vertical.
Esto nos deja con solo fuerzas horizontales y un problema unidimensional más simple. Las direcciones se indican con signos más o menos, con el derecho tomado como la dirección positiva. Ver el diagrama de cuerpo libre en la Figura 5.14.
Solución
Dado que la aceleración, la masa y la fuerza de fricción se dan, comenzamos con la segunda ley de Newton y buscamos la forma de encontrar el empuje de los motores. Hemos definido la dirección de la fuerza y la aceleración como actuando "a la derecha", por lo que debemos considerar solo las magnitudes de estas cantidades en los cálculos. Por lo tanto, comenzamos con
$$\bold{\vec{F}}_{Neta} = ma$$donde $\bold{\vec{F}}_{Neta}$ es la fuerza neta a lo largo de la dirección horizontal. Podemos ver en la figura que los empujes del motor se suman, mientras que la fricción se opone al empuje. En forma de ecuación, la fuerza externa neta es
$$\bold{\vec{F}}_{Neta} = 4T - f$$Al sustituir esto en la segunda ley de Newton nos da
$$\bold{\vec{F}}_{Neta} = ma = 4T - f$$Usando un poco de álgebra, resolvemos el empuje total 4T:
$$4T = ma + f$$Sustituyendo los valores conocidos
$$4T = ma + f = (2100kg)(49 m/s^2) + 650 N$$Por lo tanto, el empuje total es
$$4T = 1.0 \times 10^5 N$$y los empujes individuales son
$$T = \frac{1.0 \times 10^5 N}{4} = 2.5 \times 10^4 N$$Explicación
Los números son bastante grandes, por lo que el resultado podría sorprenderte. Experimentos como éste se realizaron a principios de la década de 1960 para probar los límites de la resistencia humana, y la configuración se diseñó para proteger a los sujetos humanos en las eyecciones de emergencia de los aviones de combate. Se obtuvieron velocidades de $1000 km/h$, con aceleraciones de $45g$. (Recuerda que $g$ es la aceleración debida a la gravedad, y es $9.80 m/s^2$. Cuando decimos que la aceleración es $45g$, es $45 \times 9.8 m/s^2$, que es aproximadamente $440 m/s^2$). Aunque los sujetos vivos ya no se usan, se han obtenido velocidades de $10.000 km/h$ con un trineo cohete.
En este ejemplo, como en el anterior, el sistema de interés es obvio. Vemos en ejemplos posteriores que la elección del sistema de interés es crucial, y la elección no siempre es obvia.
La segunda ley de Newton es más que una definición; es una relación entre aceleración, fuerza y masa. Nos puede ayudar a hacer predicciones. Cada una de esas cantidades físicas se puede definir de forma independiente, por lo que la segunda ley nos dice algo básico y universal sobre la naturaleza.
 Comprueba tu aprendizaje 5.4
Comprueba tu aprendizaje 5.4
Componentes rectangulares de la segunda ley de Newton
Hemos desarrollado la segunda ley de Newton y la presentamos como una ecuación vectorial en la Ecuación 5.3. Esta ecuación vectorial se puede escribir como ecuaciones de tres componentes:
$$\sum \bold{\vec{F}}_x = m\bold{\vec{a}}_x,\;\;\; \sum \bold{\vec{F}}_y = m\bold{\vec{a}}_y,\;\;\;\text{y }\sum \bold{\vec{F}}_z = m\bold{\vec{a}}_z$$La segunda ley es una descripción de cómo un cuerpo responde mecánicamente a su entorno. La influencia del entorno es la fuerza neta $\bold{\vec{F}}_{Neta}$, la respuesta del cuerpo es la aceleración $\bold{\vec{a}}$, y la fuerza de respuesta es inversamente proporcional a la masa m.
Cuanto mayor es la masa de un objeto, menor es su respuesta (su aceleración) a la influencia del entorno (una fuerza neta dada). Por lo tanto, la masa de un cuerpo es una medida de su inercia, como explicamos en la Primera Ley de Newton.
Ejemplo 5.5
Fuerza en un balón de fútbol
Un jugador lanza un balón de fútbol de $0.400 kg$ a través del campo; sufre una aceleración dada por $\bold{\vec{a}} = 3.00\^{\bold{i}} + 7.00\^{\bold{j}} m/s^2$. Halla (a) la fuerza resultante que actúa sobre la pelota y (b) la magnitud y dirección de la fuerza resultante.
Estrategia
Los vectores en formato $\^{\bold{i}}$ y $\^{\bold{j}}$, que indican la dirección de la fuerza a lo largo del eje $x$ y el eje $y$, respectivamente, están involucrados, por lo que aplicamos la segunda ley de Newton en forma de vector.
Solución
a. Aplicamos la segunda ley de Newton:
$$\bold{\vec{F}}_{Neta} = m\bold{\vec{a}} = (0.400kg)(3.00\^{\bold{i}} + 7.00\^{\bold{j}} m/s^2) = 1.20\^{\bold{i}} + 2.80\^{\bold{j}} N$$b. La magnitud y la dirección se encuentran usando los componentes de la $\bold{\vec{F}}_{Neta}$:
$$\sqrt{(1.20 N)^2 + (2.80 N)^2} = 3.05 N\;\text{ y }\;\theta = tan_{-1}\Big(\frac{2.80}{1.20}\Big) = 66.8\degree$$Explicación
Debemos recordar que la segunda ley de Newton es una ecuación vectorial.
En (a), estamos multiplicando un vector por un escalar para determinar la fuerza neta en forma de vector. Si bien la forma vectorial ofrece una representación compacta del vector fuerza, no nos dice qué tan "grande" es, o dónde va, en términos intuitivos. En (b), estamos determinando el tamaño real (magnitud) de esta fuerza y la dirección en la que viaja.
Ejemplo 5.6
Masa de un coche
Halla la masa de un automóvil si una fuerza neta de $-600.0\^{\bold{j}} N$ produce una aceleración de $-0.2\^{\bold{j}} m/s^2$.
Estrategia
La división vectorial no está definida, por lo que $m = \bold{\vec{F}}_{Neta}/\bold{\vec{a}}m $ no se puede realizar. Sin embargo, la masa $m$ es un escalar, entonces podemos usar la forma escalar de la segunda ley de Newton, $m = F_{Neta}/a.
Solución
Usamos $m = F_{Neta}/a$ y sustituimos las magnitudes de los dos vectores: $F_{Neta} = 600.0 N$ y $a = 0.2 m/s^2$. Por lo tanto,
$$m = \frac{F_{Neta}}{a} = \frac{600.0 N}{0.2 m/s^2} = 3000 kg$$Explicación
La fuerza y la aceleración se dieron en el formato $\^{\bold{i}}$ y $\^{\bold{j}}$, pero la respuesta, masa m, es un escalar y, por lo tanto, no se da en este formato.
Ejemplo 5.7
Varias fuerzas en una partícula
A una partícula de masa $m = 4.0 kgm$ se le aplican cuatro fuerzas de magnitudes $F_1 = 10.0 N, F_2 = 40.0 N, F_3 = 5.0 N$, y $F_3 = 2.0 N$, con las direcciones como se indican en el diagrama de cuerpo libre en Figura 5.15. ¿Cuál es la aceleración de la partícula?
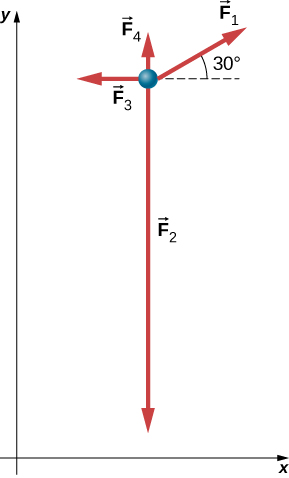
Estrategia
Debido a que este es un problema bidimensional, debemos usar un diagrama de cuerpo libre. Primero, $\bold{\vec{F}}_1$ debe resolverse en componentes $x$ e $y$. Entonces podemos aplicar la segunda ley en cada dirección.
Solución
Dibujamos un diagrama de cuerpo libre como se muestra en la Figura 5.15. Ahora aplicamos la segunda ley de Newton. Consideramos que todos los vectores se descompusieron en componentes $x$ e $y$:
$\sum\bold{\vec{F}}_x = m\bold{\vec{a}}_x\\ F_{1x} - F_{3x} = ma_x\\ F_1cos30\degree - F_{3x} = ma_x\\ (10.0 N)(cos30\degree) - 5.0 N = (4.0 kg)a_x\\ a_x = 0.92 m/s^2$
$\sum\bold{\vec{F}}_y = m\bold{\vec{a}}_y\\ F_{1y} + F_{4y} - F_{2y} = ma_y\\ F_1 sen30\degree + F_{4y} - F_{2y} = ma_y\\ (10.0 N)(sen30\degree) + 2.0 N - 40.0 N= (4.0 kg)a_y\\ a_y = -8.3 m/s^2$
Por lo tanto, la aceleración neta es
$$\bold{\vec{a}} = (0.92\^{\bold{i}} − 8.3\^{\bold{j}}) m/s^2$$que es un vector de magnitud $8,4 m/s^2$ dirigido a $276\degree$ al eje $x$ positivo.
Explicación
Se pueden encontrar numerosos ejemplos en la vida cotidiana que involucran tres o más fuerzas que actúan sobre un solo objeto, como cables que corren desde el puente Golden Gate o un jugador de fútbol que es abordado por tres defensores. Podemos ver que la solución de este ejemplo es solo una extensión de lo que ya hemos hecho.
 Comprueba tu aprendizaje 5.5
Comprueba tu aprendizaje 5.5
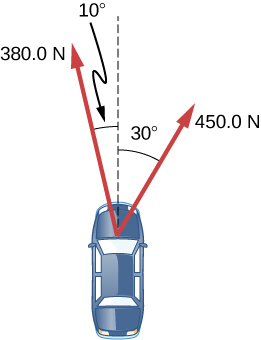
A continuación, en una escena interactiva diseñada por Juan Guillermo Rivera B., podrás observar tres ejemplos de sistemas en equilibrio. En capítulos posteriores, nos detendremos a un análisis más detallado de este tipo de aplicaciones.
La segunda ley de Newton y momentum (momento lineal)
Newton en realidad declaró su segunda ley en términos de momentum: "La velocidad instantánea a la que cambia el momento de un cuerpo es igual a la fuerza neta que actúa sobre el cuerpo" ("Tasa instantánea" implica que la derivada está involucrada).
Esto se puede dar por la ecuación vectorial
Esto significa que la segunda ley de Newton aborda la cuestión central del movimiento: ¿qué causa un cambio en el movimiento de un objeto? Momentum fue descrito por Newton como "cantidad de movimiento", una forma de combinar tanto la velocidad de un objeto como su masa. Dedicaremos el momento lineal y las colisiones al estudio del momento.
Por ahora, es suficiente definir el momentum $\bold{\vec{p}}$ como el producto de la masa del objeto $m$ y su velocidad $\bold{\vec{v}}$:
Como la velocidad es un vector, también lo es el momentum.
Es fácil visualizar el momentum. Un tren que se mueve a $10 m/s$ tiene más momento lineal que uno que se mueve a $2 m/s$. En la vida cotidiana, hablamos de un equipo deportivo como "tener ímpetu (momentum)" cuando anotan puntos contra el equipo contrario.
Si sustituimos la Ecuación 5.7 en la Ecuación 5.6, obtenemos
$$\bold{\vec{F}}-{Neta} = \frac{d\bold{\vec{p}}}{dt} = \frac{d(m\bold{\vec{v}})}{dt}$$Cuando $m$ es constante, tenemos
$$\bold{\vec{F}}-{Neta} = m\frac{d(m\bold{\vec{v}})}{dt} = m\bold{\vec{a}}$$Por lo tanto, vemos que la forma de momento de la segunda ley de Newton se reduce a la forma dada anteriormente en esta sección.
En el siguiente interactivo, crea una fuerza aplicada y observa cómo hace que los objetos se muevan.
Masa y peso
La masa y el peso a menudo se usan indistintamente en la conversación diaria. Por ejemplo, nuestros registros médicos a menudo muestran nuestro peso en kilogramos, pero nunca en las unidades correctas de newtons. En física, sin embargo, hay una distinción importante. El peso es la atracción de la Tierra sobre un objeto. Depende de la distancia desde el centro de la Tierra. A diferencia del peso, la masa no varía con la ubicación, es la misma en la Tierra, en la órbita o en la superficie de la Luna.
Unidades de fuerza
La ecuación $F_{Neta} = ma$ se usa para definir la fuerza neta en términos de masa, longitud y tiempo. Como se explicó anteriormente, la unidad de fuerza SI es el newton. Desde $F_{Neta} = ma$,
$$1\; N = 1\; kg\cdot m/s^2$$Aunque casi todo el mundo utiliza el newton para la unidad de fuerza, en los Estados Unidos, la unidad de fuerza más familiar es la libra ($lb$), donde $1 \;N = 0,225 \;lb$. Por lo tanto, una persona de $225 lb$ pesa $1000 N$.
Peso y fuerza gravitacional
Cuando se cae un objeto, acelera hacia el centro de la Tierra. La segunda ley de Newton dice que una fuerza neta sobre un objeto es responsable de su aceleración. Si la resistencia del aire es insignificante, la fuerza neta en un objeto que cae es la fuerza gravitatoria, comúnmente llamada su peso $\bold{\vec{w}}$, o su fuerza debida a la gravedad que actúa sobre un objeto de masa $m$.
El peso se puede denotar como un vector porque tiene una dirección; abajo es, por definición, la dirección de la gravedad, y por lo tanto, el peso es una fuerza descendente. La magnitud del peso se denota como $w$. Galileo instrumentalmente pudo demostrar que, en ausencia de resistencia del aire, todos los objetos caen con la misma aceleración $g$. Usando el resultado de Galileo y la segunda ley de Newton, podemos derivar una ecuación para el peso.
Considera un objeto con masa $m$ cayendo hacia la Tierra. Solo experimenta la fuerza descendente de la gravedad, que es el peso $\bold{\vec{w}}$. La segunda ley de Newton dice que la magnitud de la fuerza externa neta en un objeto es $\bold{\vec{F}}_{Neta} = m\bold{\vec{a}}$. Sabemos que la aceleración de un objeto debido a la gravedad es $\bold{\vec{a}} = \bold{\vec{g}}$. Sustituyendo en la segunda ley de Newton nos da las siguientes ecuaciones.
PESO
La fuerza gravitatoria de una masa es su peso. Podemos escribir esto en forma de vector, donde $\bold{\vec{w}}$ es el peso y $m$ es la masa, como $$\bold{\vec{w}} = m\bold{\vec{q}}\tag{5.8}$$ En forma escalar, podemos escribir $$w = mg\tag{5.9}$$
Dado que $g = 9.80 m/s^2$ en la Tierra, el peso de un objeto de $1.00 kg$ en la Tierra es $9.80 N$:
$$w = mg = (1.00 kg)(9.80 m/s^2) = 9.80N$$En el siguiente objeto interactivo, diseñado por Carlos Alberto Jaimes Vergara, podrás establecer la relación entre el peso de un objeto de masa constante y la aceleración de la gravedad en distintos cuerpos celestes.
Cuando la fuerza externa neta sobre un objeto es su peso, decimos que está en caída libre, es decir, la única fuerza que actúa sobre el objeto es la gravedad.
Sin embargo, cuando los objetos en la Tierra caen hacia abajo, nunca están verdaderamente en caída libre porque siempre hay alguna fuerza de resistencia hacia arriba desde el aire que actúa sobre el objeto.
La aceleración debido a la gravedad $g$ varía ligeramente sobre la superficie de la Tierra, por lo que el peso de un objeto depende de su ubicación y no es una propiedad intrínseca del objeto.
El peso varía dramáticamente si dejamos la superficie de la Tierra. En la Luna, por ejemplo, la aceleración debida a la gravedad es de solo $1,67 m/s^2$. Una masa de $1.0 kg$ tiene un peso de $9.8 N$ en la Tierra y solo alrededor de $1.7 N$ en la Luna.
La definición más amplia de peso en este sentido es que el peso de un objeto es la fuerza gravitacional del cuerpo grande más cercano, como la Tierra, la Luna o el Sol. Esta es la definición más común y útil de peso en física. Sin embargo, difiere dramáticamente de la definición de peso utilizada por la NASA y los medios populares en relación con el viaje espacial y la exploración. Cuando hablan de "ingravidez" y "microgravedad", se refieren al fenómeno que llamamos "caída libre" en la física. Usamos la definición anterior de peso, fuerza $\bold{\vec{w}}$ debido a la gravedad que actúa sobre un objeto de masa $m$, y hacemos una distinción cuidadosa entre la caída libre y la ingravidez real.
Ten en cuenta que el peso y la masa son cantidades físicas diferentes, aunque están estrechamente relacionadas. La masa es una propiedad intrínseca de un objeto: es una cantidad de materia. La cantidad de materia de un objeto está determinada por el número de átomos y moléculas de varios tipos que contiene. Debido a que estos números no varían, en la física newtoniana, la masa no varía; por lo tanto, su respuesta a una fuerza aplicada no varía. Por el contrario, el peso es la fuerza gravitatoria que actúa sobre un objeto, por lo que varía según la gravedad.
Por ejemplo, una persona más cerca del centro de la Tierra, a poca altura, como Nueva Orleans, pesa un poco más que una persona que se encuentra en la mayor elevación de Denver, a pesar de que pueden tener la misma masa.
Es tentador equiparar masa a peso, porque la mayoría de nuestros ejemplos tienen lugar en la Tierra, donde el peso de un objeto varía solo un poco con la ubicación del objeto. Además, es difícil contar e identificar todos los átomos y moléculas en un objeto, por lo que la masa rara vez se determina de esta manera. Si consideramos situaciones en las que $\bold{\vec{g}}$ es una constante en la Tierra, vemos que el peso $\bold{\vec{w}}$ es directamente proporcional a la masa $m$, ya que $\bold{\vec{w}} = m\bold{\vec{g}}$, es decir, cuanto más masivo es un objeto, más pesa. Operacionalmente, las masas de objetos se determinan por comparación con el kilogramo estándar, como discutimos en el capítulo de Unidades y Medición. Pero al comparar un objeto en la Tierra con uno en la Luna, podemos ver fácilmente una variación en el peso pero no en la masa. Por ejemplo, en la Tierra, un objeto de $5.0 kg$ pesa $49 N$; en la Luna, donde $g$ es $1.67 m/s^2$, el objeto pesa $8.4 N$. Sin embargo, la masa del objeto todavía es $5.0 kg$ en la Luna.
Ejemplo 5.8
Despejando un campo
Un agricultor está levantando algunas rocas moderadamente pesadas de un campo para plantar cultivos. Levanta una piedra que pesa $40.0 lb$. (aproximadamente $180 N$). ¿Qué fuerza aplica si la piedra acelera a una velocidad de $1.5 m/s^2$?
Estrategia
Nos dieron el peso de la piedra, que usamos para encontrar la fuerza neta en la piedra. Sin embargo, también necesitamos conocer su masa para aplicar la segunda ley de Newton, por lo que debemos aplicar la ecuación de peso, w = mg, para determinar la masa.
Solución
Ninguna fuerza actúa en la dirección horizontal, por lo que podemos concentrarnos en las fuerzas verticales, como se muestra en el siguiente diagrama de cuerpo libre. Marcamos la aceleración hacia un lado; técnicamente, no es parte del diagrama de cuerpo libre, pero nos ayuda a recordar que el objeto acelera hacia arriba (por lo que la fuerza neta es hacia arriba).
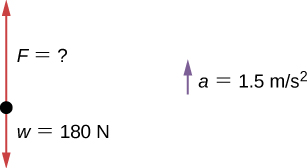
$w = mg\\ m = \frac{w}{g} = \frac{180 N}{9.8 m/s^2} = 18 kg\\ \sum F = ma\\ F - w = ma$
$F - 180 N = (18 kg)(1.5 m/s^2)\\ F - 180 N = 27 N\\ F = 207 N = 210 N (\text{ a dos cifras significativas})$
Explicación
Para aplicar la segunda ley de Newton como la ecuación primaria para resolver un problema, a veces tenemos que confiar en otras ecuaciones, como la del peso o una de las ecuaciones cinemáticas, para completar la solución.
 Comprueba tu aprendizaje 5.6
Comprueba tu aprendizaje 5.6
¿Puedes aterrizar de forma segura, como lo hizo Neil Armstrong en 1969? Presentamos una variante del videojuego clásico "Lunar Lander"Lunar Lander es un videojuego de arcade desarrollado por Atari, Inc. en 1979. El objetivo de este juego es pilotar un módulo lunar y alunizarlo de manera segura en la luna. Commodore lanzo una versión muy parecida, Jupiter Lander para su computadora VIC-20. Después, Jupiter Lander fue lanzado para la Commodore 64 y en 2009 fue lanzado para AmigaOS (wikipedia)., pero esta ves es en Marte. Simula el movimiento del módulo de aterrizaje lunar, con la masa, el empuje, la tasa de consumo de combustible y la gravedad, en esta versión, de Marte. Este clone de Lunar Lander fue diseñado por Ben Rothman.
Otro objeto interactivo interesante es "Gravedad y órbitas" desarrollado en Phet Interactive Simulations
En la siguiente escena interactiva, mueve el sol, la tierra, la luna y la estación espacial para ver cómo afecta sus fuerzas gravitatorias y trayectorias orbitales. ¡Visualiza los tamaños y las distancias entre los diferentes cuerpos celestes y desactiva la gravedad para ver lo que pasaría sin ésta!
La tercera Ley de Newton
Hasta ahora hemos considerado la fuerza como un empuje o un tirón; sin embargo, si lo piensas bien, te das cuenta que no se produce ningún empuje o atracción por sí mismo. Cuando empujas una pared, la pared te empuja hacia atrás. Esto nos lleva a la Tercera ley de Newton.
Cada vez que un cuerpo ejerce una fuerza sobre un segundo cuerpo, el primer cuerpo experimenta una fuerza que es igual en magnitud y opuesta en dirección a la fuerza que ejerce. Matemáticamente, si un cuerpo A ejerce una fuerza F→ en el cuerpo $B$, entonces $B$ ejerce simultáneamente una fuerza $-\bold{\vec{F}}$ en $A$, o en forma de ecuación vectorial, $$\bold{\vec{F}}_{AB} = -\bold{\vec{F}}_{BA}\tag{5.10}$$
La tercera ley de Newton representa una cierta simetría en la naturaleza: las fuerzas siempre ocurren en pares, y un cuerpo no puede ejercer una fuerza sobre otro sin experimentar una fuerza en sí misma. A veces nos referimos a esta ley en términos generales como "acción-reacción", donde la fuerza ejercida es la acción y la fuerza experimentada como consecuencia es la reacción. La tercera ley de Newton tiene usos prácticos para analizar el origen de las fuerzas y comprender qué fuerzas son externas a un sistema.
Podemos ver fácilmente la tercera ley de Newton observando cómo se mueven las personas. Considera la posibilidad de que una nadadora se empuje del lado de una piscina (Figura 5.16).
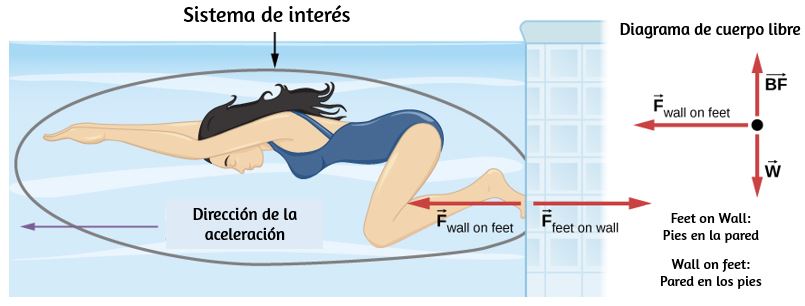
Ella empuja contra la pared de la piscina con sus pies y acelera en la dirección opuesta a la de su empuje. La pared ha ejercido una fuerza igual y opuesta sobre la nadadora. Podría pensarse que dos fuerzas iguales y opuestas se cancelarían, pero no lo hacen porque actúan en sistemas diferentes. En este caso, hay dos sistemas que podríamos investigar: la nadadora y el muro. Si seleccionamos que la nadadora sea el sistema de interés, como en la figura, entonces $F_{\text{pared en pies}}$ es una fuerza externa en este sistema y afecta su movimiento. La nadadora se mueve en la dirección de esta fuerza. Por el contrario, la fuerza $F_{\text{pies en pared}}$ actúa en la pared, no en nuestro sistema de interés.
Por lo tanto, $F_{\text{pies en pared}}$ no afecta directamente el movimiento del sistema y no cancela $F_{\text{pared en pies}}$.
La nadadora empuja en la dirección opuesta a la que desea moverse. La reacción a su impulso es, por lo tanto, en la dirección deseada. En un diagrama de cuerpo libre, como el que se muestra en la figura 5.16, nunca incluimos ambas fuerzas de un par de acción-reacción; en este caso, solo usamos $F_{\text{pared en pies}}$, no $F_{\text{pies en pared}}$.
Otros ejemplos de la tercera ley de Newton son fáciles de encontrar:
- Cuando un profesor camina frente a una pizarra, ejerce una fuerza hacia atrás en el piso. El piso ejerce una fuerza de reacción hacia el profesor que lo hace acelerar.
- Un automóvil acelera hacia adelante porque el suelo empuja hacia delante sobre las ruedas, en reacción a las ruedas que empujan hacia atrás en el suelo. Puedes ver evidencia de las ruedas empujando hacia atrás cuando las llantas giran en un camino de grava y tiran las rocas hacia atrás.
- Los cohetes avanzan expulsando el gas hacia atrás a gran velocidad. Esto significa que el cohete ejerce una gran fuerza hacia atrás sobre el gas en la cámara de combustión del cohete; por lo tanto, el gas ejerce una gran fuerza de reacción hacia adelante en el cohete. Esta fuerza de reacción, que empuja un cuerpo hacia adelante en respuesta a una fuerza hacia atrás, se llama empuje. Es un concepto erróneo común que los cohetes se impulsan empujando en el suelo o en el aire detrás de ellos. De hecho, funcionan mejor en el vacío, donde pueden expulsar más fácilmente los gases de escape.
- Los helicópteros crean elevación empujando el aire hacia abajo, experimentando así una fuerza de reacción hacia arriba.
- Las aves y los aviones también vuelan ejerciendo una fuerza en el aire en una dirección opuesta a la de cualquier fuerza que necesiten. Por ejemplo, las alas de un pájaro fuerzan el aire hacia abajo y hacia atrás para levantarlo y avanzar.
- Un pulpo se impulsa en el agua expulsando agua a través de un embudo de su cuerpo, similar a un jet ski.
- Cuando una persona tira de una cuerda vertical, la cuerda detiene la persona (Figura 5.17).

Hay dos características importantes de la tercera ley de Newton. Primero, las fuerzas ejercidas (la acción y la reacción) son siempre iguales en magnitud pero opuestas en la dirección. En segundo lugar, estas fuerzas actúan sobre diferentes cuerpos o sistemas: la fuerza de $A$ actúa sobre $B$ y $B$ sobre $A$. En otras palabras, las dos fuerzas son fuerzas distintas que no actúan en el mismo cuerpo. Por lo tanto, no se cancelan entre sí.
Para la situación que se muestra en la figura 5.6, la tercera ley indica que debido a que la silla está empujando hacia arriba al estudiante con fuerza $\bold{\vec{C}}$, él está empujando hacia abajo la silla con fuerza $-\bold{\vec{C}}$.
Del mismo modo, él está presionando hacia abajo con las fuerzas $-\bold{\vec{F}}$ y $-\bold{\vec{T}}$ en el piso y la mesa, respectivamente. Finalmente, dado que la Tierra tira hacia abajo del estudiante con fuerza $\bold{\vec{w}}$, tira hacia arriba en la Tierra con la fuerza $-\bold{\vec{w}}$. Si ese estudiante golpeara con enojo la mesa con frustración, aprendería rápidamente la dolorosa lección (evitable estudiando las leyes de Newton) de que la mesa le devuelve la misma dureza.
Una persona que está caminando o corriendo aplica la tercera ley de Newton instintivamente. Por ejemplo, el corredor de la figura 5.18 empuja hacia atrás en el suelo para que el suelo lo empuje hacia adelante.
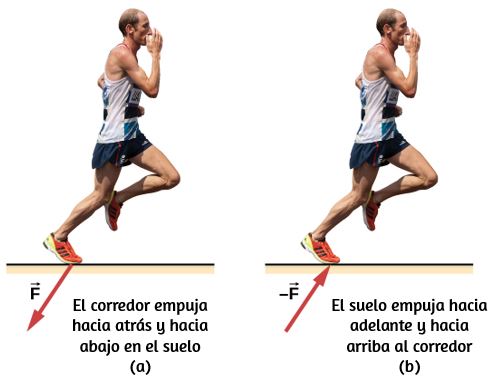
Ejemplo 5.9
Fuerzas en un objeto estático
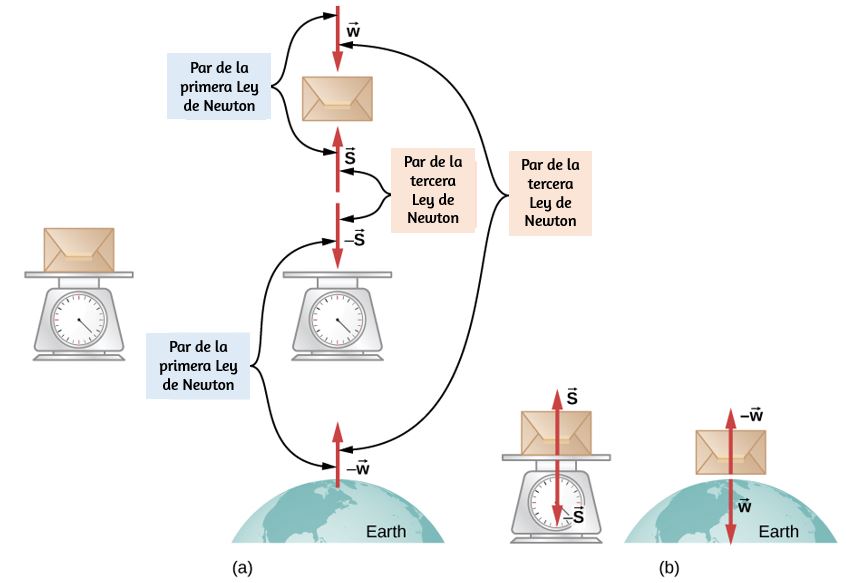
El paquete en la Figura 5.19 está apoyado en una balanza. Las fuerzas en el paquete son $\bold{\vec{S}}$, que se debe a la balanza, y $-\bold{\vec{w}}$, que se debe al campo gravitacional de la Tierra.
Las fuerzas de reacción que ejerce el paquete son $-\bold{\vec{S}}$ en la balanza y $\bold{\vec{w}}$ en la Tierra. Debido a que el paquete no se está acelerando, la aplicación de la segunda ley produce
$$\bold{\vec{S}} - \bold{\vec{w}} = m\bold{\vec{a}} = 0$$Entonces,
$$\bold{\vec{S}}S = \bold{\vec{w}}$$Por lo tanto, la lectura de la escala da la magnitud del peso del paquete. Sin embargo, la balanza no mide el peso del paquete; mide la fuerza $-\bold{\vec{S}}$ en su superficie. Si el sistema se está acelerando, $\bold{\vec{S}}$ y $- \bold{\vec{w}}$ no serían iguales, como se explicará en las Aplicaciones de las Leyes de Newton.
Ejemplo 5.10
Eligiendo el sistema correcto
Una profesora de física empuja un carrito de equipos de demostración a una sala de conferencias (Figura 5.20). Su masa es de $65.0 kg$, la masa del carro es de $12.0 kg$ y la masa del equipo es de $7.0 kg$. Calcula la aceleración producida cuando la profesora ejerce una fuerza hacia atrás de $150 N$ en el piso. Todas las fuerzas que se oponen al movimiento, como la fricción en las ruedas del carro y la resistencia del aire, suman $24.0 N$.
Estrategia
Como aceleran como una unidad, definimos el sistema como el profesor, el carro y el equipo. Este es el Sistema 1 en la Figura 5.20.
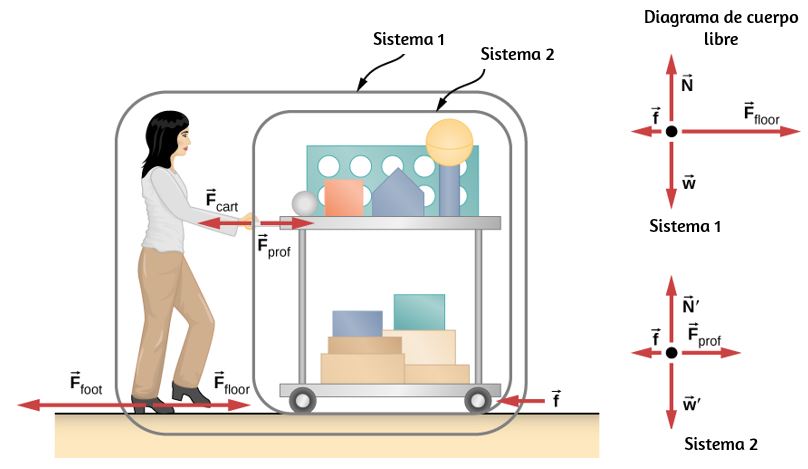
El profesor empuja hacia atrás con una fuerza $F_{pie}$ ($F_{foot}$ en la figura) de $150 N$. De acuerdo con la tercera ley de Newton, el suelo ejerce una fuerza de reacción hacia adelante $F_{piso}= 150 N (F_{floor})$ en el Sistema 1. Como todo movimiento es horizontal, podemos suponer que no hay fuerza neta en la dirección vertical . Por lo tanto, el problema es unidimensional a lo largo de la dirección horizontal.
Como se indicó, la fricción $f$ se opone al movimiento y, por lo tanto, está en la dirección opuesta a $F_{piso}$. No incluimos las fuerzas indicadas en la figura como $F_{prof}$ o $F_{cart}$ porque estas son fuerzas internas, y no incluimos $F_{pie}$ porque actúa en el piso, no en el sistema. No hay otras fuerzas significativas que actúen en el Sistema 1. Si la fuerza externa neta puede encontrarse a partir de toda esta información, podemos usar la segunda ley de Newton para encontrar la aceleración según lo solicitado. Ver el diagrama de cuerpo libre en la figura.
Solución
La segunda ley de Newton nos dice que,
$$a = \frac{\bold{\vec{F}}_{Neta}}{m}$$La fuerza externa neta en el Sistema 1 se deduce de la Figura 5.20 y de las discusiones anterior es,
$$\bold{\vec{F}}_{Neta} -f = 150 N - 24.0 N = 126 N.$$La masa del Sistema 1 es
$$m = (65.0 + 12.0 + 7.0) kg = 84 kg$$Estos valores de $\bold{\vec{F}}_{Neta}$ y $m$ producen una aceleración de: $$a = \frac{\bold{\vec{F}}_{Neta}}{m} = \frac{126 N}{85 kg} = 1.5 m/s^2$$
Explicación
Ninguna de las fuerzas entre componentes del Sistema 1, como entre las manos de la profesora y el carro, contribuyen a la fuerza externa neta porque son internas al Sistema 1. Otra forma de ver esto es que las fuerzas entre los componentes de un sistema se cancelan porque son iguales en magnitud y opuestos en dirección. Por ejemplo, la fuerza ejercida por la profesora sobre el carro da como resultado una fuerza igual y opuesta de vuelta a la profesora. En este caso, ambas fuerzas actúan en el mismo sistema y, por lo tanto, se cancelan. Por lo tanto, las fuerzas internas (entre los componentes de un sistema) se cancelan. Elegir el Sistema 1 fue crucial para resolver este problema.
Ejemplo 5.11
Fuerza en el carro: elegir un nuevo sistema
Calcula la fuerza que ejerce la profesora en el carrito de la Figura 5.20, utilizando datos del ejemplo anterior si es necesario.
Estrategia
Si definimos el sistema de interés como el carro más el equipo (Sistema 2 en la Figura 5.20), entonces la fuerza externa neta en el Sistema 2 es la fuerza que la profesora ejerce sobre el carro menos la fricción. La fuerza que ejerce sobre el carro, $F_{profe}$, es una fuerza externa que actúa sobre el Sistema 2. $F_{profe}$ era interno al Sistema 1, pero es externo al Sistema 2 y, por lo tanto, entra en la segunda ley de Newton para este sistema.
Solución
La segunda ley de Newton se puede usar para encontrar $F_{profe}$. Comenzamos
$$ a = \frac{\bold{\vec{F}}_{Neta}}{m}$$La magnitud de la fuerza externa neta en el Sistema 2 es
$$\bold{\vec{F}}_{Neta} = \bold{\vec{F}}_{profe} - f$$Despejamos $\bold{\vec{F}}_{profe}$,
$$\bold{\vec{F}}_{profe} = \bold{\vec{F}}_{Neta} + f$$Se da el valor de $f$, por lo que debemos calcular $\bold{\vec{F}}_{Neta}$. Eso se puede hacer porque se conocen tanto la aceleración como la masa del Sistema 2. Usando la segunda ley de Newton, vemos que:
$$\bold{\vec{F}}_{Neta} = ma$$donde la masa del Sistema 2 es $19.0 kg (m = 12.0kg + 7.0kg)$ y su aceleración fue de $1.5 m /s^2$ en el ejemplo anterior. Así,
$$\bold{\vec{F}}_{profe} = \bold{\vec{F}}_{Neta} + f = 29 N + 24.0 N = 53 N$$Explicación
Esta fuerza es significativamente menor que la fuerza de $150 N$ que la profesora ejerció hacia atrás en el suelo. No toda esa fuerza de $150 N $se transmite al carro; algo de ella acelera a la profesora.
La elección de un sistema es un paso analítico importante tanto para resolver problemas como para comprender a fondo la física de la situación (que no necesariamente son las mismas cosas)
 Comprueba tu aprendizaje 5.7
Comprueba tu aprendizaje 5.7
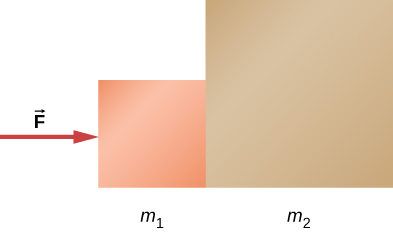
En el siguiente objeto interactivo, diseñado por Carlos Alberto Serrato Hernández , podrás manipular la masa de un objeto que es empujado por una persona. Se observan las fuerzas de acción y reacción que intervienen en este evento.
Las gráficas muestran las variaciones en la aceleración y la velocidad tanto del patinador como de la caja, así como el desplazamiento que experimentan.
Fuerzas comunes
Las fuerzas reciben muchos nombres, como empujar, tirar, punzar y pesar. Tradicionalmente, las fuerzas se han agrupado en varias categorías y nombres relacionados con su fuente, cómo se transmiten o sus efectos. Varias de estas categorías se discuten en esta sección, junto con algunas aplicaciones interesantes. Más ejemplos de fuerzas se discuten más adelante en este texto.
Un catálogo de fuerzas: normal, tensión y otros ejemplos de fuerzas
Un catálogo de fuerzas será útil como referencia ya que resolvemos varios problemas relacionados con la fuerza y el movimiento. Estas fuerzas incluyen fuerza normal, tensión, fricción y fuerza de resorte.
Fuerza normal
El peso (también llamado la fuerza de la gravedad) es una fuerza penetrante que actúa en todo momento y debe contrarrestarse para evitar la caída de un objeto. Debes sostener el peso de un objeto pesado empujándolo hacia arriba cuando lo mantienes estático, como se ilustra en la Figura 5.21 (a). Pero, ¿cómo los objetos inanimados como una mesa soportan el peso de una masa colocada sobre ellos, como se muestra en la Figura 5.21 (b)? Cuando la bolsa de comida para perros se coloca sobre la mesa, la mesa se hunde levemente debajo de la carga. Esto sería notable si la carga se coloca en una mesa de cartas, pero incluso una mesa de roble resistente se deforma cuando se aplica una fuerza sobre ella. A menos que un objeto se deforme más allá de su límite, ejercerá una fuerza de restauración muy similar a la de un resorte deformado (o un trampolín). Cuanto mayor es la deformación, mayor es la fuerza de restauración. Por lo tanto, cuando la carga se coloca sobre la mesa, la mesa se hunde hasta que la fuerza de restauración llega a ser tan grande como el peso de la carga.
En este punto, la fuerza externa neta en la carga es cero. Esa es la situación cuando la carga está estática sobre la mesa. La mesa se hunde rápidamente y el pandeo es leve, por lo que no lo notamos. Pero es similar a la caída de un trampolín cuando subes a él.
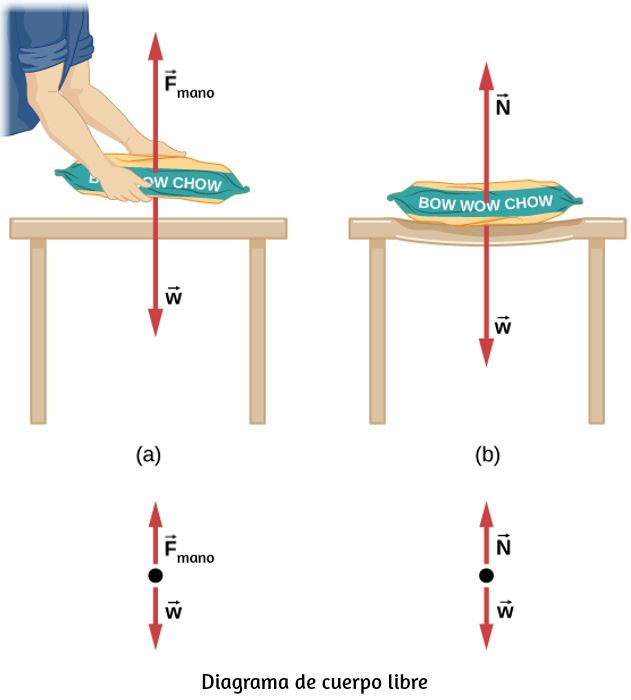
Debemos concluir que cualquier cosa que soporte una carga, ya sea animada o no, debe suministrar una fuerza ascendente igual al peso de la carga, como asumimos en algunos de los ejemplos anteriores. Si la fuerza que soporta el peso de un objeto, o una carga, es perpendicular a la superficie de contacto entre la carga y su soporte, esta fuerza se define como una fuerza normal y aquí viene dada por el símbolo $\bold{\vec{N}}$. (Esta no es la unidad newton para fuerza, o $N$). La palabra normal significa perpendicular a una superficie. Esto significa que la fuerza normal experimentada por un objeto que descansa sobre una superficie horizontal puede expresarse en forma vectorial de la siguiente manera:
En forma escalar,
La fuerza normal puede ser menor que el peso del objeto si el objeto está en una pendiente.
Ejemplo 5.12
Peso en un plano inclinado
Considera al esquiador en la pendiente en la Figura 5.22. Su masa, incluido el equipo, es de $60.0 kg$. (a) ¿Cuál es su aceleración si la fricción es insignificante? (b) ¿Cuál es su aceleración si la fricción es de $45.0 N$?
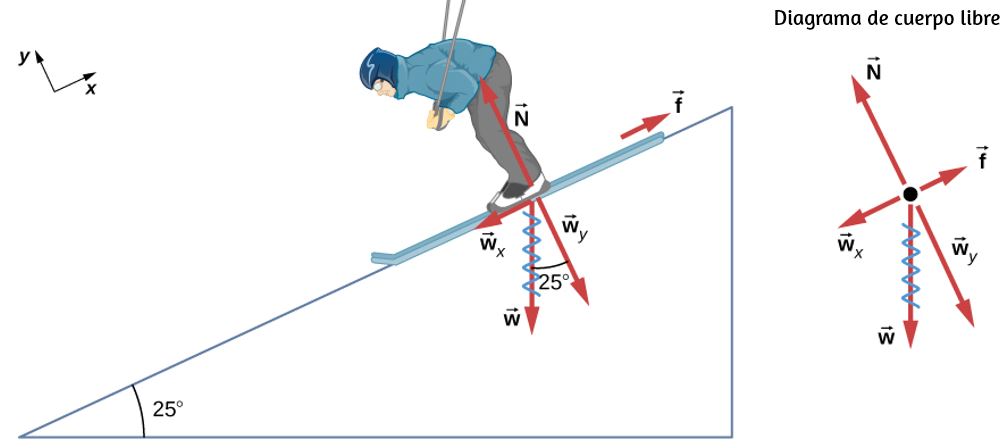
Estrategia
Este es un problema bidimensional, ya que no todas las fuerzas en el esquiador (el sistema de interés) son paralelas. El enfoque que hemos utilizado en la cinemática bidimensional también funciona bien aquí. Elije un sistema de coordenadas conveniente y proyecta los vectores en sus ejes, creando dos problemas unidimensionales para resolver. El sistema de coordenadas más conveniente para el movimiento en un plano inclinado es uno que tiene una coordenada paralela a la pendiente y otra perpendicular a la pendiente.
Los movimientos a lo largo de ejes mutuamente perpendiculares son independientes. Usamos $x$ e $y$ para las direcciones paralelas y perpendiculares, respectivamente. Esta elección de ejes simplifica este tipo de problema, porque no hay movimiento perpendicular a la pendiente y la aceleración es descendente. En cuanto a las fuerzas, la fricción se dibuja en oposición al movimiento (la fricción siempre se opone al movimiento hacia adelante) y siempre es paralela al plano inclinado, $w_x$ se dibuja paralelo al plano inclinado y cuesta abajo (causa el movimiento del esquiador cuesta abajo), y $w_y$ se dibuja como el componente de peso perpendicular a la pendiente o plano inclinado. Entonces, podemos considerar los problemas separados de fuerzas paralelas a la pendiente y fuerzas perpendiculares a la pendiente.
Solución
La magnitud del componente de peso paralelo a la pendiente es
$$w_x = wsen25\degree = mgsen25\degree$$y la magnitud del componente del peso perpendicular a la pendiente es
$$w_y = wcos25\degree = mgcos25\degree$$a. Desprecia la fricción. Como la aceleración es paralela a la pendiente, solo necesitamos considerar fuerzas paralelas a la pendiente. (Las fuerzas perpendiculares a la pendiente se suman a cero, ya que no hay aceleración en esa dirección.) Las fuerzas paralelas a la pendiente son el componente del peso del esquiador paralelo a la pendiente $w_x$ y la fricción $f$. Usando la segunda ley de Newton, con subíndices para denotar cantidades paralelas a la pendiente,
donde $\bold{\vec{F}}_{Neta x} = w_x = mgsen25\degree$, suponiendo que no haya fricción para esta parte. Por lo tanto,
$$\begin{split} a_x &= \frac{\bold{\vec{F}}_{Neta x}}{m} = \frac{mgsen25\degree}{m} \\ &= gsen25\degree = (9.80 m/s^2)(0.4226)\\ &= 4.14 m/s^2 \end{split}$$b. Incluye fricción. Tenemos un valor dado para la fricción, y sabemos que su dirección es paralela a la pendiente y se opone al movimiento entre las superficies en contacto. Entonces la fuerza externa neta es
$$\bold{\vec{F}}_{Neta x} = w_x − f$$>Sustituyendo esto en la segunda ley de Newton, $a_x = \frac{\bold{\vec{F}}_{Neta x}}{m}$, obtenemos
$$a_x = \frac{\bold{\vec{F}}_{Neta x}}{m} = \frac{w_x - f}{m} = \frac{mgsen25\degree - f}{m}$$Sustituyendo por los valores conocidos
$$a_x = \frac{(60.0 kg)(9.80 m/s^2)(0.4226)− 45.0 N}{60.0 kg} = 3.39 m/s^2$$que es la aceleración paralela al plano inclinado cuando hay 45.0 N de fricción opuesta.
Explicación
Como la fricción siempre se opone al movimiento entre superficies, la aceleración es menor cuando hay fricción que cuando no hay ninguna. Es un resultado general que si la fricción en un plano inclinado es despreciable, entonces la aceleración hacia abajo de la pendiente es $a = gsen\theta$, independientemente de la masa. Como se discutió anteriormente, todos los objetos caen con la misma aceleración en ausencia de resistencia al aire. Del mismo modo, todos los objetos, independientemente de la masa, se deslizan hacia abajo por una inclinación sin fricción con la misma aceleración (si el ángulo es el mismo).
Cuando un objeto descansa sobre un plano inclinado que forma un ángulo $\theta$ con la horizontal, la fuerza de gravedad que actúa sobre el objeto se divide en dos componentes: una fuerza que actúa perpendicular al plano, $w_y$, y una fuerza que actúa paralela al plano, $w_x$ (Figura 5.23). La fuerza normal $\bold{\vec{N}}$ es típicamente igual en magnitud y opuesta en dirección al componente perpendicular del peso $w_y$. La fuerza que actúa paralela al plano, $w_x$, hace que el objeto se acelere por la pendiente.
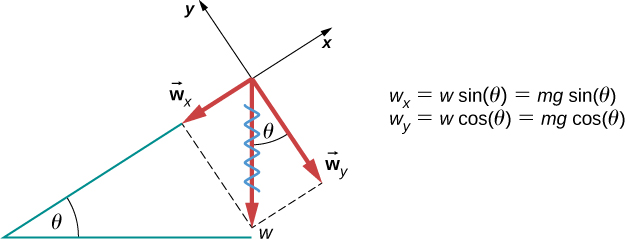
Ten cuidado al descomponer el peso del objeto en sus componentes. Si la inclinación está en un ángulo $\theta$ respecto a la horizontal, entonces las magnitudes de los componentes de peso son
$$w_x = wsen\theta = mgsen\theta$$y
$$w_y = wcos\theta = mgcos\theta$$Usamos la segunda ecuación para escribir la fuerza normal generada un objeto que descansa sobre un plano inclinado:
En lugar de memorizar estas ecuaciones, es útil poder determinarlas a partir de la razón. Para hacer ésto, dibujamos el ángulo recto formado por los tres vectores de peso. El ángulo $\theta$ de la inclinación es el mismo que el formado entre $w$ y $w_y$. Al conocer esta propiedad, podemos utilizar la trigonometría para determinar la magnitud de los componentes de peso:
$$cos\theta = \frac{w_y}{w}\;\text{ con }\;w_y = wcos\theta = mgcos\theta$$$$sen\theta = \frac{w_x}{w}\;\text{ con }\;w_x = wsen\theta = mgsen\theta$$
 Comprueba tu aprendizaje 5.8
Comprueba tu aprendizaje 5.8
Tensión
Una tensión es una fuerza a lo largo de un elemento; en particular, es una fuerza de tracción que actúa a lo largo de un conector flexible estirado, como una cuerda o cable. La palabra "tensión" proviene de una palabra latina que significa "estirar". No es coincidencia que los cordones flexibles que llevan las fuerzas musculares a otras partes del cuerpo se denominen tendones.
Cualquier conector flexible, como una cuerda, cadena, cable o alambre, solo puede ejercer un tirón paralelo a su longitud; por lo tanto, una fuerza portada por un conector flexible es una tensión con una dirección paralela al conector. La tensión es un tirón en un conector. Considera la frase: "No puedes empujar una cuerda". En cambio, la fuerza de tensión se extiende hacia afuera a lo largo de los dos extremos de una cuerda.
Considera a una persona sosteniendo una masa en una cuerda, como se muestra en la Figura 5.24. Si la masa de $5.00 kg$ en la figura es estática, entonces su aceleración es cero y la fuerza neta es cero.
Las únicas fuerzas externas que actúan sobre la masa son su peso y la tensión suministrada por la cuerda. Así,
$$F_{Neta} = T − w = 0$$donde $T$ y $w$ son las magnitudes de la tensión y el peso, respectivamente, y sus signos indican dirección, siendo positivo hacia arriba. Como probamos usando la segunda ley de Newton, la tensión es igual al peso de la masa soportada:
Por lo tanto, para una masa de $5.00 kg$ (despreciando la masa de la cuerda), vemos que
$$\begin{split} T &= mg\\ &= (5.00 kg)(9.80 m/s^2)\\ &= 49.0N \end{split}$$Si cortamos la cuerda e insertamos un resorte, el resorte se extendería a una longitud correspondiente a una fuerza de $49.0 N$, proporcionando una observación directa y una medida de la fuerza de tensión en la cuerda.
Los conectores flexibles a menudo se utilizan para transmitir fuerzas alrededor de las esquinas, como en un sistema de tracción del hospital, un tendón o un cable de freno de bicicleta. Si no hay fricción, la transmisión de tensión no se reduce; solo su dirección cambia, y siempre es paralela al conector flexible, como se muestra en la Figura 5.25.
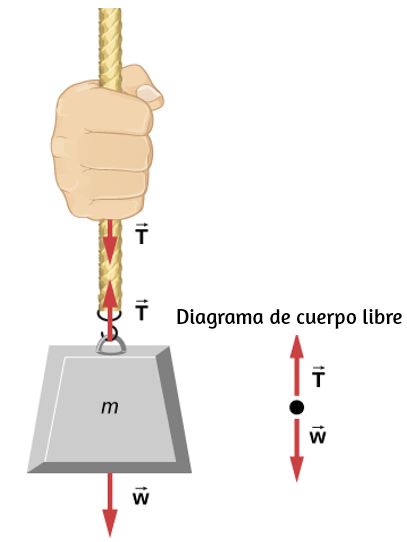 Cuando un conector perfectamente flexible (que no requiere fuerza para doblarlo) como esta cuerda transmite una fuerza $\bold{\vec{T}}$, esa fuerza debe ser paralela a la longitud de la cuerda, como se muestra. Según la tercera ley de Newton, la cuerda tira con la misma fuerza pero en direcciones opuestas en la mano y la masa apoyada (despreciando el peso de la cuerda). La cuerda es el medio que lleva las fuerzas iguales y opuestas entre los dos objetos. La tensión en cualquier parte de la cuerda entre la mano y la masa es igual. Una vez que has determinado la tensión en un lugar, has determinado la tensión en todos los lugares a lo largo de la cuerda.
Cuando un conector perfectamente flexible (que no requiere fuerza para doblarlo) como esta cuerda transmite una fuerza $\bold{\vec{T}}$, esa fuerza debe ser paralela a la longitud de la cuerda, como se muestra. Según la tercera ley de Newton, la cuerda tira con la misma fuerza pero en direcciones opuestas en la mano y la masa apoyada (despreciando el peso de la cuerda). La cuerda es el medio que lleva las fuerzas iguales y opuestas entre los dos objetos. La tensión en cualquier parte de la cuerda entre la mano y la masa es igual. Una vez que has determinado la tensión en un lugar, has determinado la tensión en todos los lugares a lo largo de la cuerda.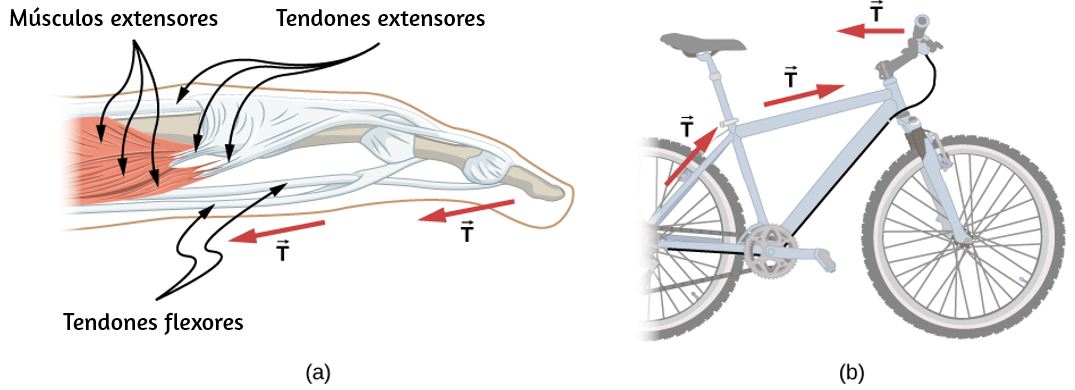
Ejemplo 5.13
¿Cuál es la tensión en una cuerda floja?
Calcula la tensión en el cable que soporta la cuerda floja de $70.0 kg$ que se muestra en la Figura 5.26.
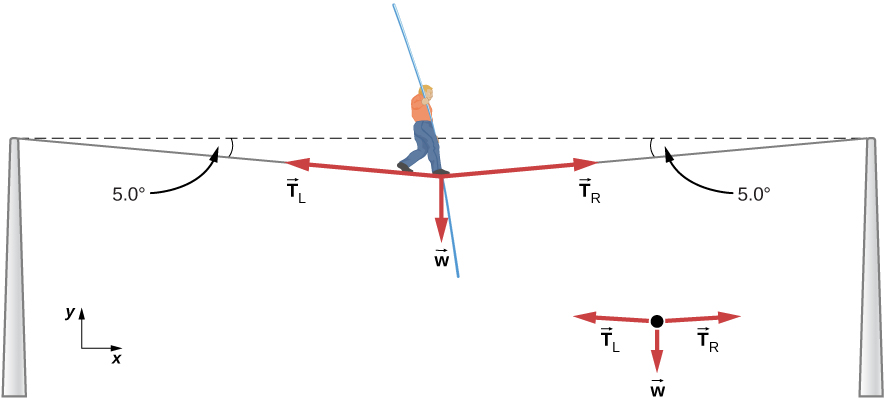
Estrategia
Como puedes ver en la Figura 5.26, el cable se dobla debajo del peso de la persona. Por lo tanto, la tensión en ambos lados de la persona tiene un componente ascendente que puede soportar su peso.
Como de costumbre, las fuerzas son vectores representados pictóricamente por flechas que tienen la misma dirección que las fuerzas y longitudes proporcionales a sus magnitudes. El sistema es el equilibrista, y las únicas fuerzas externas que actúan sobre él son su peso $\bold{\vec{w}}$ y las dos tensiones $\bold{\vec{T}}_L$ (tensión izquierda) y $\bold{\vec{T}}_R$ (tensión derecha).
Es razonable despreciar el peso del cable. La fuerza externa neta es cero, porque el sistema es estático. Podemos usar la trigonometría para encontrar las tensiones. Una conclusión es posible desde el principio: podemos ver en la Figura 5.26 (b) que las magnitudes de las tensiones $T_L$ y $T_R$ deben ser iguales. Sabemos esto porque no hay aceleración horizontal en la cuerda y las únicas fuerzas que actúan hacia la izquierda y la derecha son $T_L$ y $T_R$. Por lo tanto, la magnitud de esas componentes horizontales de las fuerzas debe ser igual para que se cancelen unas a otras.
Siempre que tengamos problemas de vectores bidimensionales en los que no haya dos vectores paralelos, el método más fácil de solución es elegir un sistema de coordenadas conveniente y proyectar los vectores en sus ejes. En este caso, el mejor sistema de coordenadas tiene un eje horizontal ($x$) y un eje vertical ($y$).
Solución
Primero, necesitamos hallar los vectores de tensión en sus componentes horizontales y verticales. Ayuda observar un nuevo diagrama de cuerpo libre que muestra todos los componentes horizontales y verticales de cada fuerza que actúa sobre el sistema (Figura 5.27).
Considera las componentes horizontales de las fuerzas (denotados con un subíndice x):
$$\bold{\vec{F}}_{Neta\; x} = T_{Rx} - T_{Lx}$$La fuerza horizontal externa es $F_{Neta\; x} = 0$, ya que la persona está estática. Así,
$$F_{Neta\; x} = 0 = T_{Rx} - T_{Lx} \implies T_{Rx} = T_{Lx}$$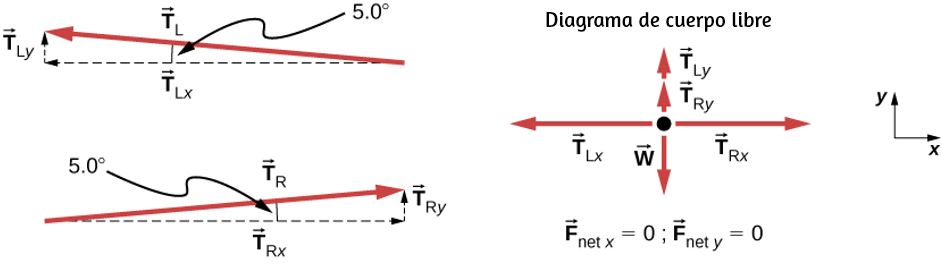
Ahora observa la Figura 5.27. Puedes usar la trigonometría para determinar la magnitud de $T_L$ y $T_R$:
$$cos5.0\degree = \frac{T_{Lx}}{T_L}\; \text{con}\; T_{Lx} = T_Lcos5.0\degree$$ $$cos5.0\degree = \frac{T_{Rx}}{T_L}\; \text{con}\; T_{Rx} = T_L cos5.0\degree$$Igualando $T_{Lx}$ y $T_{Rx}$
$$T_L cos5.0\degree = T_R cos5.0\degree \implies T_L = T_R = T$$como se predijo. Ahora, considerando los componentes verticales (señalados por un subíndice y), podemos hallar $T$. De nuevo, dado que la persona está estática, la segunda ley de Newton implica que $F_{Neta\; y} = 0$. Por lo tanto, como se ilustra en el diagrama de cuerpo libre,
$$F_{Neta\; y} = T_{Ly} + T_{Ry} − w = 0$$Podemos usar la trigonometría para determinar las relaciones entre $T_{Ly}, T_{Ry}$ y $T$. Como determinamos a partir del análisis en la dirección horizontal, $T_L = T_R = T$:
$$sen 5.0\degree = \frac{T_{Ly}}{T_L}\; \text{con }\;T_{Ly} = T_L sen 5.0\degree$$ $$sen 5.0\degree = \frac{T_{Ry}}{T_L}\; \text{con}\; T_{Ry} = T_L sen 5.0\degree$$Ahora podemos sustituir los valores de $T_{Ly}$ y $T_{Ry}$ por la ecuación de fuerza neta en la dirección vertical:
$$F_{Neta\; y} = T_{Ly} + T_{Ry} − w = 0$$ $F_{Neta\; y} = Tsen 5.0\degree + Tsen 5.0\degree° − w = 0$$ $$2Tsen 5.0\degree = w$$luego,
$$T = \frac{w}{2sen 5.0\degree} = \frac{mg}{2sen 5.0\degree$$Finalmente, obtenemos:
$$T = \frac{(70.0kg)(9.80m/s^2)}{2(0.0872)}= 3930 N$$Explicación
La tensión vertical en el cable actúa como una fuerza que soporta el peso del equilibrista. La tensión es casi seis veces mayor que el peso $686 N$ del equilibrista. Como el cable es casi horizontal, la componente vertical de su tensión es solo una fracción de la tensión en el cable.
Los grandes componentes horizontales están en direcciones opuestas y se cancelan, por lo que la mayor parte de la tensión en el cable no se usa para soportar el peso del equilibrista.
Si deseamos crear una gran tensión, todo lo que tenemos que hacer es ejercer una fuerza perpendicular a un conector flexible y tenso, como se ilustra en la figura 5.26.
Como vimos en el ejemplo 5.13, el peso de la cuerda floja actúa como una fuerza perpendicular a la cuerda. Vimos que la tensión en la cuerda está relacionada con el peso del equilibrista de la siguiente manera:
$$T = \frac{w}{2sen\theta}$$Podemos extender esta expresión para describir la tensión $T$ creada cuando se ejerce una fuerza perpendicular $(F\perp)$ en el medio de un conector flexible:
$$T = \frac{F\perp}{2sen\theta}$$El ángulo entre la horizontal y el cable está representado por $\theta$. En este caso, $T$ se vuelve grande a medida que $\theta$ se aproxima a cero. Incluso el peso relativamente pequeño de cualquier conector flexible hará que se pandee, ya que se produciría una tensión infinita si fuera horizontal (es decir, $\theta = 0$ y $sen \theta = 0$). Por ejemplo, la figura 5.28 muestra una situación en la que deseamos sacar un automóvil del barro cuando no hay una grúa disponible. Cada vez que el automóvil se mueve hacia adelante, la cadena se ajusta para mantenerlo lo más recto posible. La tensión en la cadena viene dada por $T = \frac{F\perp}{ 2sen\theta}$, y como $\theta$ es pequeño, $T $es grande.
Esta situación es análoga a la del equilibrista, excepto que las tensiones que se muestran aquí son las transmitidas al automóvil y al árbol en lugar de las que actúan en el punto donde se aplica $F\perp$.

 Comprueba tu aprendizaje 5.9
Comprueba tu aprendizaje 5.9
En la Aplicaciones de las Leyes de Newton, ampliamos la discusión sobre la tensión en un cable para incluir casos en los que los ángulos mostrados no son iguales. Situación que anticipamos con el interactivo presentado en las siguiente página.
Fricción
La fricción es una fuerza resistiva que se opone al movimiento o a su tendencia. Imagina un objeto en reposo en una superficie horizontal. La fuerza neta que actúa sobre el objeto debe ser cero, lo que lleva a la igualdad del peso y la fuerza normal, que actúan en direcciones opuestas.
Si la superficie está inclinada, la fuerza normal equilibra el componente del peso perpendicular a la superficie. Si el objeto no se desliza hacia abajo, el componente del peso paralelo al plano inclinado se equilibra con la fricción. La fricción se analiza con mayor detalle en el próximo capítulo.
El siguiente objeto interactivo, diseñado por Carlos Alberto Serrato Hernández, muestra un equilibrista recorriendo una cuerda en monociclo. En la parte superior se observan las magnitudes de las fuerzas que actúan sobre la cuerda en cada instante. En este caso se pueden observar ángulos diferentes para $T_{Lx}$ y $T_{Rx}$.
Fuerza de un resorte
Un resorte es un medio especial con una estructura atómica específica que tiene la capacidad de restaurar su forma, si se deforma. Para restaurar su forma, un resorte ejerce una fuerza de restauración que es proporcional a su deformación en la dirección opuesta en la que se estira o comprime. Esta es la declaración de una ley conocida como ley de Hooke, que tiene la forma matemática
$$\bold{\vec{F}} = −k\bold{\vec{x}}$$La constante de proporcionalidad $k$ es una medida de la rigidez del resorte. La línea de acción de esta fuerza es paralela al eje del resorte, y el sentido de la fuerza está en la dirección opuesta del vector de desplazamiento (Figura 5.29). El desplazamiento debe medirse desde la posición relajada; $x = 0$ cuando el muelle está quieto.
Fuerzas reales y marcos inerciales
Hay otra distinción entre fuerzas: algunas fuerzas son reales, mientras que otras no. Las fuerzas reales tienen algún origen físico, como un tirón gravitacional. Por el contrario, las fuerzas ficticias surgen simplemente porque un observador se encuentra en un marco de referencia acelerado o no original, como uno que gira (como un tiovivo) o que experimenta una aceleración lineal (como un coche disminuyendo la velocidad). Por ejemplo, si un satélite se dirige hacia el norte sobre el hemisferio norte de la Tierra, entonces a un observador en la Tierra, parecerá que experimenta una fuerza hacia el oeste que no tiene un origen físico. En cambio, la Tierra está girando hacia el este y se mueve hacia el este bajo el satélite. En el marco de la Tierra, esto parece una fuerza hacia el oeste en el satélite, o puede interpretarse como una violación de la primera ley de Newton (la ley de la inercia).
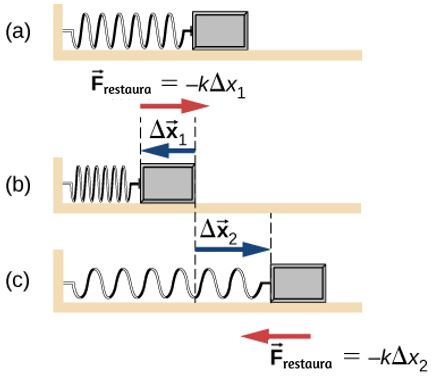
Podemos identificar una fuerza ficticia haciendo la pregunta, "¿Cuál es la fuerza de reacción?" Si no podemos nombrar la fuerza de reacción, entonces la fuerza que estamos considerando es ficticia. En el ejemplo del satélite, la fuerza de reacción debería ser una fuerza hacia el este en la Tierra. Recuerda que un marco de referencia inercial es aquel en el que todas las fuerzas son reales y, de manera equivalente, una en la que las leyes de Newton tienen las formas simples dadas en este capítulo.
La rotación de la Tierra es lo suficientemente lenta como para que la Tierra sea casi un marco inercial. Normalmente debes realizar experimentos precisos para observar las fuerzas ficticias y las ligeras desviaciones de las leyes de Newton, como el efecto que acabamos de describir.
A gran escala, como para la rotación de los sistemas meteorológicos y las corrientes oceánicas, los efectos se pueden observar fácilmente (Figura 5.30).

El factor crucial para determinar si un marco de referencia es inercial es si se acelera o gira en relación a un marco inercial conocido.
A menos que se indique lo contrario, todos los fenómenos discutidos en este texto están en marcos inerciales.
Las fuerzas discutidas en esta sección son fuerzas reales, pero no son las únicas fuerzas reales. La elevación y el empuje, por ejemplo, son fuerzas reales más especializadas. En la larga lista de fuerzas, ¿hay algunas más básicas que otras? ¿Hay algunas manifestaciones diferentes de la misma fuerza subyacente? La respuesta a ambas preguntas es sí, como verás en el tratamiento de la física moderna más adelante en el texto.
En el interactivo anterior, diseñado en https://phet.colorado.edu/, puedes experimentar con la Ley de Hooke. Estira y comprime los resortes para explorar las relaciones entre la fuerza y la constante del resorte. Investiga lo que ocurre cuando dos resortes están conectados en serie y en paralelo.
Dibujando diagramas de cuerpo libre
El primer paso para describir y analizar la mayoría de los fenómenos en física implica el dibujo cuidadoso de un diagrama de cuerpo libre. Los diagramas de cuerpo libre se han usado en ejemplos a lo largo de este capítulo. Recuerda que un diagrama de cuerpo libre solo debe incluir las fuerzas externas que actúan sobre el cuerpo de interés.
Una vez que hemos dibujado un diagrama preciso de cuerpo libre, podemos aplicar la primera ley de Newton si el cuerpo está en equilibrio (fuerzas equilibradas, es decir, $F_{Neta} = 0$) o la segunda ley de Newton si el cuerpo se está acelerando (fuerza desequilibrada; es, $F_{Neta}\ne 0$).
Estrategia de resolución de problemas: construcción de diagramas de cuerpo libre
Observa las siguientes reglas para construir un diagrama de cuerpo libre:
- Dibuja el objeto bajo consideración; no tiene que ser artístico. Al principio, es posible que desees dibujar un círculo alrededor del objeto de interés para asegurarte de centrarte en etiquetar las fuerzas que actúan sobre el objeto.
Si estás tratando el objeto como una partícula (sin tamaño ni forma ni rotación), representa el objeto como un punto. A menudo colocamos este punto en el origen de un sistema de coordenadas $xy$. - Incluye todas las fuerzas que actúan sobre el objeto, representando estas fuerzas como vectores. Considera los tipos de fuerzas descritas en el apartado anterior (fuerza normal, fricción, tensión y fuerza de resorte, así como el peso y la fuerza aplicada).
No incluyas la fuerza neta en el objeto. Con la excepción de la gravedad, todas las fuerzas que hemos discutido requieren contacto directo con el objeto. Sin embargo, las fuerzas que el objeto ejerce sobre su entorno no deben incluirse. Nunca incluimos ambas fuerzas de un par de acción y reacción.
- Convierte el diagrama de cuerpo libre en un diagrama más detallado que muestre los componentes x e y de una fuerza dada (esto a menudo es útil cuando se resuelve un problema usando la primera o la segunda ley de Newton). En este caso, coloca una línea ondulada a través del vector original para mostrar que ya no está en juego: se ha reemplazado por sus componentes $x$ e $y$.
- Si hay dos o más objetos, o cuerpos, en el problema, dibuja un diagrama separado de cuerpo libre para cada objeto.
Nota: Si hay aceleración, no la incluimos directamente en el diagrama de cuerpo libre; sin embargo, puede ayudar el indicar la aceleración fuera del diagrama de cuerpo libre. Puedes etiquetarlo en un color diferente para indicar que está separado del diagrama de cuerpo libre.
Vamos a aplicar la estrategia de resolución de problemas al dibujar un diagrama de cuerpo libre para un trineo. En la figura figura 5.31 (a), un trineo es tirado por la fuerza P en un ángulo de 30°. En la parte (b), mostramos un diagrama de cuerpo libre para esta situación, como se describe en los pasos 1 y 2 de la estrategia de resolución de problemas. En la parte (c), mostramos todas las fuerzas en términos de sus componentes $x$ e $y$, de acuerdo con el paso 3.
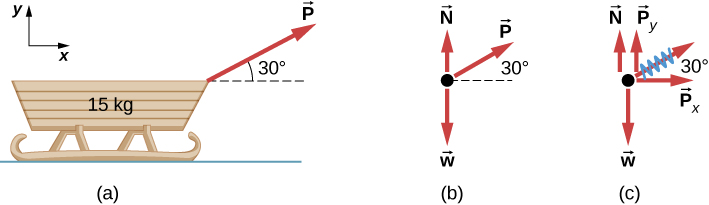
Ejemplo 5.14
Dos bloques en un plano inclinado
Construye el diagrama de cuerpo libre para el objeto $A$ y el objeto $B$ mostrados en la figura 5.32.
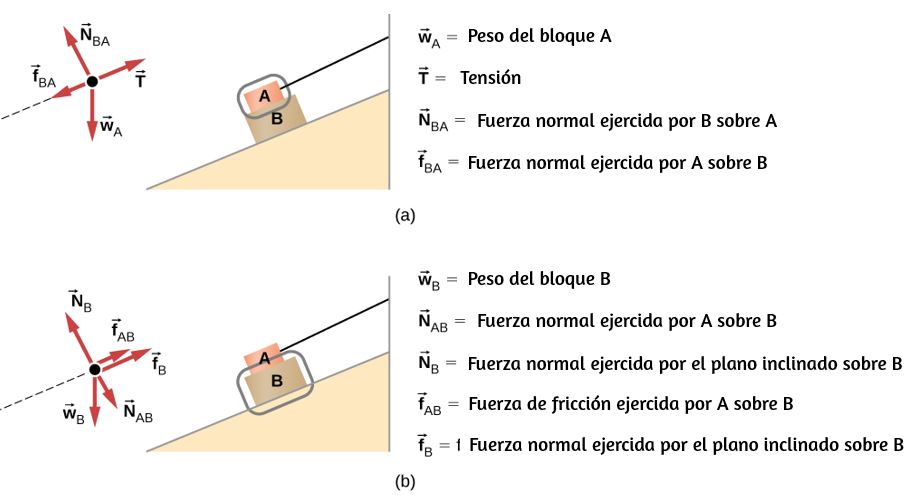
Estrategia
Seguimos los cuatro pasos enumerados en la estrategia de resolución de problemas.
Solución
Comenzamos creando un diagrama para el primer objeto de interés. En la figura 5.32 (a), el objeto A está aislado (en un círculo) y representado por un punto.
Ahora incluimos cualquier fuerza que actúe sobre el cuerpo. Aquí, no hay fuerza aplicada presente. El peso del objeto actúa como una fuerza que apunta verticalmente hacia abajo, y la presencia del cable indica una fuerza de tensión que apunta en dirección opuesta al objeto. El objeto A tiene una interfaz y, por lo tanto, experimenta una fuerza normal, alejada de la interfaz.
La fuente de esta fuerza es el objeto $B$, y esta fuerza normal está etiquetada. Como el objeto B tiene tendencia a deslizarse hacia abajo, el objeto $A$ tiene tendencia a deslizarse hacia arriba con respecto a la interfaz, por lo que la fricción $f_{BA}$ se dirige hacia abajo en paralelo al plano inclinado.
Como se señaló en el paso 4 de la estrategia de resolución de problemas, luego construimos el diagrama de cuerpo libre en la Figura 5.32 (b) usando el mismo enfoque. El objeto B experimenta dos fuerzas normales y dos fuerzas de fricción debido a la presencia de dos superficies de contacto. La interfaz con el plano inclinado ejerce fuerzas externas de $N_B$ y $f_B$, y la interfaz con el objeto $B$ ejerce la fuerza normal $N_{AB}$ y la fricción $f_{AB}$; $N_{AB}$ se aleja del objeto $B$, y $f_{AB}$ se opone a la tendencia del movimiento relativo del objeto $B$ con respecto al objeto $A$.
Explicación
El objeto bajo consideración en cada parte de este problema fue marcado con un círculo en gris.
Cuando aprendas por primera vez cómo dibujar diagramas de cuerpo libre, te resultará útil hacer un círculo alrededor del objeto antes de decidir qué fuerzas están actuando sobre ese objeto en particular. Esto enfoca tu atención, evitando que considere fuerzas que no están actuando sobre el cuerpo.
Ejemplo 5.15
Dos bloques en contacto
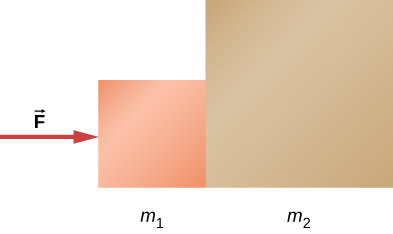 Se aplica una fuerza a dos bloques en contacto, como se muestra en la figura de la derecha.
Se aplica una fuerza a dos bloques en contacto, como se muestra en la figura de la derecha.
Estrategia
Dibuja un diagrama de cuerpo libre para cada bloque. Asegúrate de considerar la tercera ley de Newton en la interfaz donde se tocan los dos bloques.
Solución
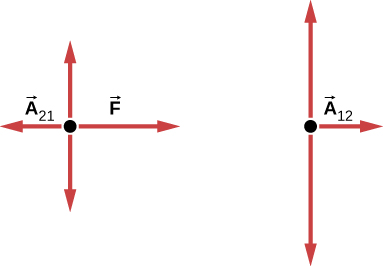
Ejemplo 5.16
Bloque en la mesa (bloques acoplados)
Un bloque descansa sobre la mesa, como se muestra. Una cuerda ligera está unida a ella y pasa sobre una polea. El otro extremo de la cuerda está unido a un segundo bloque. Se dice que los dos bloques están acoplados. El bloque $m_2$ ejerce una fuerza debido a su peso, lo que hace que el sistema (dos bloques y una cuerda) se acelere.
Estrategia
Suponemos que la cuerda no tiene masa para que no tengamos que considerarla como un objeto separado. Dibuja un diagrama de cuerpo libre para cada bloque.
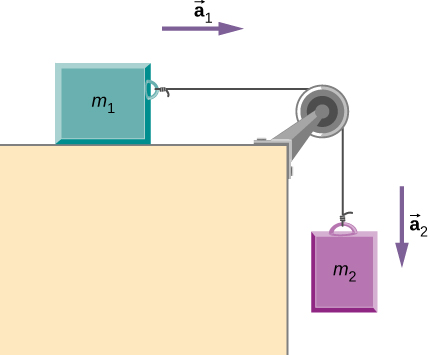
Solución
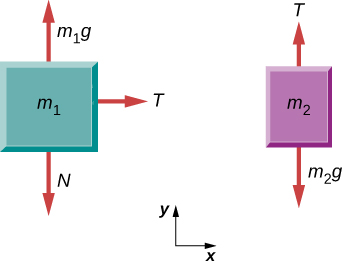
Explicación
Cada bloque se acelera (observa las etiquetas que se muestran para $\bold{\vec{a}}_1$ y $\bold{\vec{a}}_2$; sin embargo, suponiendo que la cuerda permanezca tensa, aceleran a la misma velocidad. Por lo tanto, tenemos $\bold{\vec{a}}_1 = \bold{\vec{v}}_2$. Si tuviéramos que seguir resolviendo el problema, podríamos simplemente llamarlos como aceleración $\bold{\vec{a}}$. Además, usamos dos diagramas de cuerpo libre porque usualmente encontramos la tensión $T$, lo que puede requerir que usemos un sistema de dos ecuaciones en este tipo de problema. La tensión es la misma tanto en $m_1$ como en $m_2$.
 Comprueba tu aprendizaje 5.10
Comprueba tu aprendizaje 5.10
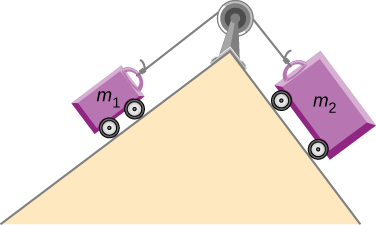
En este puzle, diseñado por Juan Guillermo Rivera B., descubre frases de Newton.
En el siguiente objeto interactivo, del repositorio de https://phet.colorado.edu/, se explica la tercera ley de Newton para las fuerzas gravitatorias, para ello, visualiza la fuerza gravitacional que dos objetos ejercen el uno sobre el otro. Ajusta las propiedades de los objetos para ver cómo el cambio de las propiedades afecta la atracción gravitacional.
Dinámica: Aplicaciones
de las leyes de Newton
La primera y segunda ley de Newton, en latín, en la edición original de su obra Principia Mathematica (https://es.wikipedia.org/)
Introducción

Las carreras de autos han crecido en popularidad en los últimos años. A medida que cada auto se mueve en una trayectoria curva alrededor del viraje, sus ruedas también giran rápidamente. Las ruedas completan muchas revoluciones, mientras que el automóvil forma solo una parte (un arco circular). ¿Cómo podemos describir las velocidades, aceleraciones y fuerzas involucradas? ¿Qué fuerza impide que un auto de carreras gire, golpeando la pared que bordea la pista? ¿Qué proporciona esta fuerza? ¿Por qué está la pista ladeada? Respondemos todas estas preguntas en este capítulo a medida que ampliamos nuestra consideración de las leyes de movimiento de Newton.
Solución de problemas con las leyes
de Newton
El éxito en la resolución de problemas es necesario para comprender y aplicar los principios físicos. Desarrollamos un patrón de análisis y
configuración de soluciones a problemas que involucran las Leyes del movimiento de Newton; en este capítulo, continuamos discutiendo estas estrategias y aplicando un proceso paso a paso.
Estrategias para resolver problemas
Seguimos aquí los conceptos básicos de resolución de problemas presentados anteriormente en este texto, pero enfatizamos estrategias específicas que son útiles para aplicar las leyes de movimiento de Newton. Una vez que identifiques los principios físicos involucrados en el problema y determines que incluyen las leyes de movimiento de Newton, puedes aplicar estos pasos para encontrar una solución. Estas técnicas también refuerzan conceptos que son útiles en muchas otras áreas de la física. Muchas estrategias de resolución de problemas se expresan directamente en los ejemplos trabajados, por lo que las siguientes técnicas deben reforzar las habilidades que ya has comenzado a desarrollar.
- Identifica los principios físicos involucrados al enumerar los datos y las cantidades que se calcularán.
- Dibuja la situación, usando flechas para representar todas las fuerzas.
- Determina el sistema de interés. El resultado es un diagrama de cuerpo libre que es esencial para resolver el problema.
- Aplica la segunda ley de Newton para resolver el problema. Si es necesario, aplica las ecuaciones cinemáticas apropiadas.
- Verifica la solución para ver si es razonable.
Apliquemos esta estrategia de resolución de problemas al desafío de levantar un piano de cola en un apartamento de un segundo piso. Una vez que hemos determinado que las leyes del movimiento de Newton están involucradas (si el problema involucra fuerzas), es particularmente importante hacer un esquema cuidadoso de la situación. Tal esquema se muestra en la figura 6.2 (a).
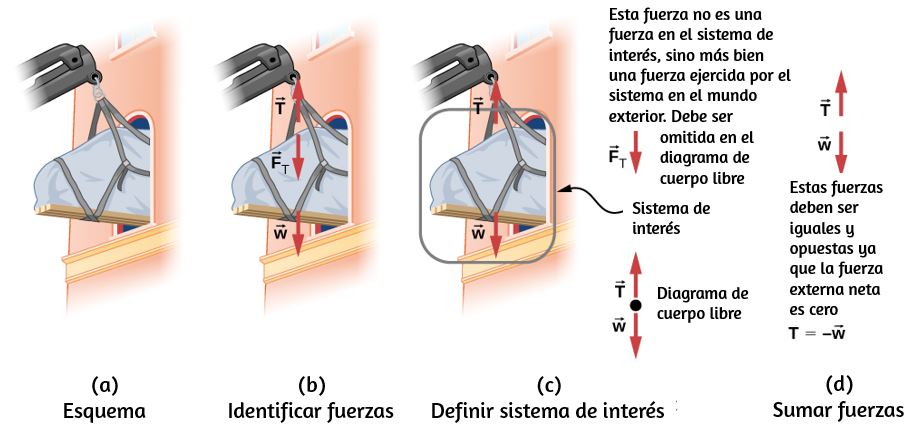
Luego, como en la figura 6.2 (b), podemos representar todas las fuerzas con flechas. Siempre que haya suficiente información, es mejor etiquetar estas flechas con cuidado y hacer que la longitud y dirección de cada una correspondan a la fuerza representada.
Al igual que en la mayoría de los problemas, debemos identificar lo que se debe determinar y lo que se sabe o se puede inferir del problema, es decir, hacer una lista de conocimientos e incógnitas. Es particularmente crucial identificar el sistema de interés, ya que la segunda ley de Newton implica solo fuerzas externas. Entonces podemos determinar qué fuerzas son externas y cuáles internas, un paso necesario para emplear la segunda ley de Newton. (Véase la figura 6.2 (c)). La tercera ley de Newton se puede usar para identificar si se ejercen fuerzas entre los componentes de un sistema (interno) o entre el sistema y algo externo (externo). Como se ilustra en Las leyes del movimiento de Newton, el sistema de interés depende de la pregunta que necesitamos responder. Solo las fuerzas se muestran en diagramas de cuerpo libre, no la aceleración o la velocidad. Hemos dibujado varios diagramas de cuerpo libre en ejemplos trabajados previos. La figura 6.2 (c) muestra un diagrama de cuerpo libre para el sistema de interés. Ten en cuenta que no se muestran fuerzas internas en un diagrama de cuerpo libre.
Una vez que se dibuja un diagrama de cuerpo libre, aplicamos la segunda ley de Newton. Esto se hace en la figura 6.2 (d) para una situación particular. En general, una vez que las fuerzas externas se identifican claramente en los diagramas de cuerpo libre, debe ser una tarea sencilla ponerlos en forma de ecuación y hallar los datos desconocidos, como se hizo en todos los ejemplos anteriores. Si el problema es unidimensional, es decir, si todas las fuerzas son paralelas, entonces las fuerzas se pueden manejar algebraicamente. Si el problema es bidimensional, debe dividirse en un par de problemas unidimensionales.
Hacemos esto proyectando los vectores de fuerza en un conjunto de ejes elegidos por conveniencia. Como se vio en ejemplos anteriores, la elección de los ejes puede simplificar el problema. Por ejemplo, cuando se trata de una inclinación, es más conveniente un conjunto de ejes con un eje paralelo a la inclinación y uno perpendicular a él. Casi siempre es conveniente hacer un eje paralelo a la dirección del movimiento, si este se conoce.
En general, simplemente escribe la segunda ley de Newton en componentes a lo largo de las diferentes direcciones. Entonces, tienes las siguientes ecuaciones:
$$F_x = ma_x, F_y = ma_y$$(Si, por ejemplo, el sistema está acelerando horizontalmente, entonces puedes establecer $a_y = 0$). Necesitamos esta información para determinar las fuerzas desconocidas que actúan en un sistema.
Como siempre, debemos verificar la solución. En algunos casos, es fácil determinar si la solución es razonable. Por ejemplo, es razonable encontrar que la fricción hace que un objeto se deslice por una pendiente más lentamente que cuando no existe fricción. En la práctica, la intuición se desarrolla gradualmente a través de la resolución de problemas; con la experiencia, cada vez es más fácil juzgar si una respuesta es razonable. Otra forma de verificar una solución es verificar las unidades. Si resolvemos la fuerza y terminamos con unidades de milímetros por segundo, cometemos un error.
Hay muchas aplicaciones interesantes de las leyes del movimiento de Newton, algunas más de las cuales se presentan en esta sección. Estos sirven también para ilustrar algunas sutilezas adicionales de la física y para ayudar a desarrollar habilidades para resolver problemas.
Vemos primero los problemas que involucran el equilibrio de partículas, que hacen uso de la primera ley de Newton, y luego consideramos la aceleración de partículas, que implica la segunda ley de Newton.
Equilibrio de partículas
Recuerda que una partícula en equilibrio es aquella para la cual las fuerzas externas están equilibradas.
El equilibrio estático involucra objetos en reposo, y el equilibrio dinámico involucra objetos en movimiento sin aceleración, pero es importante recordar que estas condiciones son relativas. Por ejemplo, un objeto puede estar en reposo cuando se ve desde nuestro marco de referencia, pero el mismo objeto parece estar en movimiento cuando lo ve alguien que se mueve a una velocidad constante. Ahora hacemos uso del conocimiento obtenido en las Leyes del movimiento de Newton, con respecto a los diferentes tipos de fuerzas y el uso de diagramas de cuerpo libre, para resolver problemas adicionales en el equilibrio de partículas.
Ejemplo 6.1
Diferentes tensiones en diferentes ángulos
Considera el semáforo (masa de $15,0 kg$) suspendido de dos cables como se muestra en la figura 6.3. Encuentra la tensión en cada cable, despreciando las masas de los cables.
Estrategia
El sistema de interés es el semáforo, y su diagrama de cuerpo libre se muestra en la figura 6.3 (c).
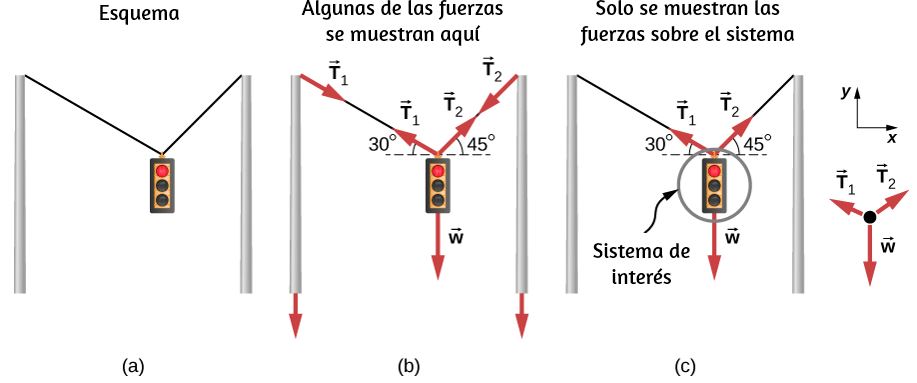
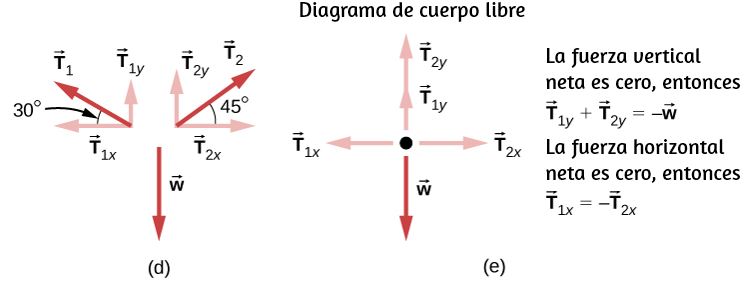
Las tres fuerzas involucradas no son paralelas, por lo que deben proyectarse en un sistema de coordenadas. El sistema de coordenadas más conveniente tiene un eje vertical y uno horizontal, y las proyecciones vectoriales se muestran en la figura 6.3 (d). Hay dos incógnitas en este problema ($T_1$ y $T_2$), por lo que se necesitan dos ecuaciones para encontrarlas.
Estas dos ecuaciones provienen de la aplicación de la segunda ley de Newton a lo largo de los ejes vertical y horizontal, señalando que la fuerza externa neta es cero a lo largo de cada eje porque la aceleración es cero.
Solución
Primero considere el eje horizontal o $x$:
$$F_{neta\; x} = T_{2x} - T_{1x} = 0$$Por lo tanto, como era de esperar,
$$T_{1x} - T_{2x}$$Esto nos da la siguiente relación:
$$T_1cos30\degree - T_2cos45\degree$$Así,
$$T_2 = 1.225T_1$$Ten en cuenta que $T_1$ y $T_2$ no son iguales en este caso porque los ángulos de cada lado no son iguales. Es razonable que $T_2$ termine siendo mayor que $T_1$ porque su aplicación es más vertical que $T_1$.
Ahora considera los componentes de fuerza a lo largo del eje vertical o $y$:
$$F_{neta\; y} = T_{1y} + T_{2y} - w = 0$$Esto implica que $T_{1y} + T_{2y} = w$.
Al sustituir estas expresiones por los componentes verticales obtenemos
$$T_1sen30\degree + T_2sen45\degree = w$$Hay dos incógnitas en esta ecuación, pero al sustituir la expresión por $T_2$ en términos de $T_1$ se reduce a una ecuación con una incognita:
$$T_1(0.500) + (1.225T_1)(0.707) = w = mg$$simplificando:
$$1.366T_1 = (15.0 kg)(9.80 m/s^2)$$La resolución de esta última ecuación da la magnitud de $T_1$
$$T_1 = 108 N$$Finalmente, encontramos la magnitud de $T_2$ usando la relación entre ellos, $T_2 = 1.225T_1$, así obtenemos
$$T_2 = 132 N$$
Explicación
Ambas tensiones serían más grandes si ambos cables fueran más horizontales, y serán iguales si y solo si los ángulos de cada lado son los mismos (como lo fueron en el ejemplo anterior del equilibrista).
Aceleración de partículas
Hemos dado una variedad de ejemplos de partículas en equilibrio. Ahora volvemos nuestra atención a los problemas de aceleración de partículas, que son el resultado de una fuerza neta no nula.
Consulta nuevamente los pasos dados al principio de esta sección y observa cómo se aplican a los siguientes ejemplos.
Ejemplo 6.2
Fuerza de arrastre en una barcaza
Dos remolcadores empujan una barcaza en diferentes ángulos (Figura 6.4). El primer remolcador ejerce una fuerza de $2.7 \times 10^5 N$ en la dirección $x$, y el segundo remolcador ejerce una fuerza de $3.6 \times 10^5 N$ en la dirección $y$. La masa de la barcaza es de $5.0 \times 10^6 kg$ y su aceleración es de $7.5 \times 10^{-2} m/s^2$ en la dirección que se muestra. ¿Cuál es la fuerza de arrastre del agua en la barcaza que resiste el movimiento? (Nota: La fuerza de arrastre es una fuerza de fricción ejercida por fluidos, como el aire o el agua. La fuerza de arrastre se opone al movimiento del objeto. Como la barcaza tiene fondo plano, podemos suponer que la fuerza de arrastre es opuesta al movimiento de la barcaza.)
Estrategia
Las direcciones y las magnitudes de aceleración y las fuerzas aplicadas se dan en la figura 6.4 (a). Definimos la fuerza total de los remolcadores en la barcaza como $\bold{\vec{F}}_{app}$, tal que
$$\bold{\vec{F}}_{app} = \bold{\vec{F}}_1 + \bold{\vec{F}}_2$$El arrastre del agua $\bold{\vec{F}}_D$ está en la dirección opuesta a la dirección del movimiento del barco; esta fuerza trabaja así contra $\bold{\vec{F}}_{app}$, como se muestra en el diagrama de cuerpo libre en la figura 6.4 (b). El sistema de interés aquí es la barcaza, ya que las fuerzas sobre ella se dan, así como su aceleración.
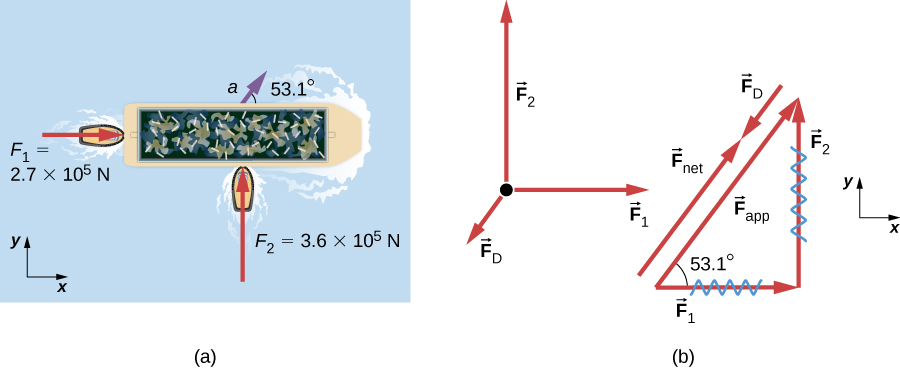
Debido a que las fuerzas aplicadas son perpendiculares, los ejes $x$ e $y$ están en la misma dirección que $\bold{\vec{F}}_1$ y $\bold{\vec{F}}_2$. El problema se convierte rápidamente en un problema unidimensional en la dirección de $\bold{\vec{F}}_{app}$, ya que la fricción es en la dirección opuesta a $\bold{\vec{F}}_{app}$. Nuestra estrategia es encontrar la magnitud y la dirección de la fuerza aplicada neta $\bold{\vec{F}}_{app}$ y luego aplicar la segunda ley de Newton para hallar la fuerza de arrastre $\bold{\vec{F}}_D$.
Solución
Como $F_x$ y $F_y$ son perpendiculares, podemos encontrar la magnitud y dirección de $\bold{\vec{F}}_{app}$ directamente. Primero, la magnitud de la resultante viene dada por el teorema de Pitágoras:
$$\begin{split} F_{app} &= \sqrt{F_1^2 + F_2^2} \\ &= \sqrt{(2.7 \times 10^5 N)^2 + (3.6 \times 10^5 N)^2} \\ &= 4.5 \times 10^5 N \end{split}$$El ángulo está dado por
$$\theta = tan^{-1}\bigg(\frac{F_2}{F_1}\bigg) = tan^{-1}\bigg(\frac{3.6 \times 10^5 N}{2.7 \times 10^5 N}\bigg) = 53.1\degree$$Según la primera ley de Newton, sabemos que esta es la misma dirección que la aceleración. También sabemos que $\bold{\vec{F}}_D$ está en la dirección opuesta a $\bold{\vec{F}}{_app}$, ya que actúa para ralentizar la aceleración. Por lo tanto, la fuerza externa neta está en la misma dirección que $\bold{\vec{F}}_{app}$, pero su magnitud es ligeramente menor. El problema ahora es unidimensional. Del diagrama de cuerpo libre, podemos ver que
$$F_{neta} = F_{app} - F_D$$Sin embargo, la segunda ley de Newton establece que
$$F_{neta} = ma$$Entonces, $F_{app} - F_D = ma$
Esto se puede resolver con la magnitud de la fuerza de arrastre del agua $F_D$ en términos de las cantidades conocidas:
$$F_D = F_{app} - ma$$Al sustituir los valores conocidos, obtenemos
$$\begin{split} F_D &= (4.5 \times 10^5 N) − (5.0 \times 10^6 kg)(7.5 \times 10^{-2} m/s^2)\\ &= 7.5 \times 10^4 N \end{split}$$La dirección de $\bold{\vec{F}}_D$ ya se ha determinado que está en la dirección opuesta a $\bold{\vec{F}}_{app}$, o en un ángulo de $53\degree$ al suroeste.
Explicación
Los números utilizados en este ejemplo son razonables para una barcaza moderadamente grande. Es ciertamente difícil obtener aceleraciones más grandes con remolcadores, y se desean velocidades pequeñas para evitar que la barcaza entre en los muelles. El arrastre es relativamente pequeño para un casco bien diseñado a baja velocidad, consistente con la respuesta a este ejemplo, donde $F_D$ es menor a $1/600$ del peso del barco.
En las Leyes del movimiento de Newton, hablamos de la fuerza normal, que es una fuerza de contacto que actúa de manera normal a la superficie de modo que un objeto no tiene una aceleración perpendicular a la superficie. La báscula de baño es un excelente ejemplo de una fuerza normal que actúa sobre un cuerpo. Proporciona una lectura cuantitativa de cuánto debe empujar hacia arriba para soportar el peso de un objeto. ¿Pero puedes predecir lo que verías en la esfera de una báscula de baño si te subes a ella durante un viaje en ascensor?.
¿Verás un valor mayor que tu peso cuando el ascensor arranque? ¿Qué pasa cuando el elevador se mueve hacia arriba a una velocidad constante? Adivina antes de leer el siguiente ejemplo.
Ejemplo 6.3
¿Qué lee la báscula de baño en un ascensor?
La figura 6.5 muestra un hombre de $75.0 kg$ (peso de alrededor de $165 lb$) parado en una báscula de baño en un elevador. Calcula la lectura de la báscula: (a) si el elevador acelera hacia arriba a una velocidad de $1.20 m/s^2$, y (b) si el elevador se mueve hacia arriba a una velocidad constante de $1 m/s$.
Estrategia
Si la báscula en reposo es precisa, su lectura es igual a $\bold{\vec{F}}_p$, que es la magnitud de la fuerza que la persona ejerce hacia abajo sobre ella. La figura 6.5 (a) muestra las numerosas fuerzas que actúan sobre el elevador, la báscula y la persona. Hace que este problema unidimensional parezca mucho más formidable que si se elige a la persona como el sistema de interés y se dibuja un diagrama de cuerpo libre, como en la figura 6.5 (b). El análisis del diagrama de cuerpo libre usando las leyes de Newton puede producir respuestas tanto a la figura 6.5 (a) como a la (b) de este ejemplo, así como a algunas otras preguntas que puedan surgir. Las únicas fuerzas que actúan sobre la persona son su peso $\bold{\vec{w}}$ y la fuerza hacia arriba de la báscula $\bold{\vec{F}}_S$. De acuerdo con la tercera ley de Newton, $\bold{\vec{F}}_p$ y $\bold{\vec{F}}_S$ son iguales en magnitud y opuestos en dirección, por lo que necesitamos encontrar $F_S$ para encontrar lo que lee la báscula. Podemos hacer esto, como siempre, aplicando la segunda ley de Newton, $\bold{\vec{F}}_{neta} = m\bold{\vec{a}}$.
Del diagrama de cuerpo libre, vemos que $\bold{\vec{F}}_{neta} = \bold{\vec{F}}_{S} - \bold{\vec{w}}$, entonces tenemos
$$F_S - w = ma$$La solución para $F_S$ nos da una ecuación con solo una incognita:
$$F_S = ma + w$$o, porque $w = mg$, simplemente
$$F_S = ma + mg$$No se hicieron suposiciones sobre la aceleración, por lo que esta solución debería ser válida para una variedad de aceleraciones además
de las de esta situación. (Nota: estamos considerando el caso cuando el elevador está acelerando hacia arriba. Si el elevador está acelerando hacia abajo, la segunda ley de Newton se convierte en $F_S - w = -ma$).
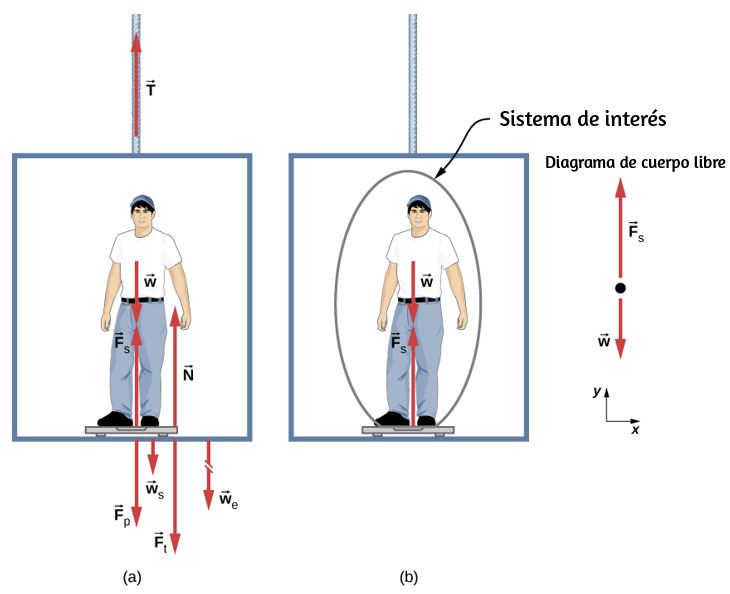
Solución
a. Tenemos $a = 1.20 m/s^2$, por lo que
$$F_S = (75.0kg)(9.80 m/s^2) + (75.0kg)(1.20 m/s^2)$$Obtenemos,
$$F_S = 825 N$$b. Ahora, ¿qué sucede cuando el elevador alcanza una velocidad constante hacia arriba? ¿La balanza aún leerá más que su peso? Para cualquier velocidad constante, la aceleración ascendente, descendente o estática es cero porque $a = \frac{\Delta v}{\Delta 1}$ y $\Delta v = 0$. Así,
$$F_S = ma + mg = 0 + mg$$o
$$F_S = (75.0 kg)(9.80 m/s^2)\\ F_S = 735 N$$Explicación
La lectura de la báscula en la figura 6.5 (a) es de aproximadamente $185 lb$. ¿Qué leyó la báscula si estuviera parado? Como su aceleración sería cero, la fuerza de la escala sería igual a su peso:
$$F_{neta} = ma = 0 = F_S - w\\ F_S = w = mg$$ $$F_S = (75.0 kg)(9.80 m/s^2) = 735 N$$Por lo tanto, la lectura de la báscula en el elevador es mayor que su peso de $735 N (165 lb)$. Esto significa que la balanza está empujando hacia arriba a la persona con una fuerza mayor que su peso, como debe hacerlo para acelerarlo hacia arriba. Claramente, cuanto mayor sea la aceleración del elevador, mayor será la lectura de la báscula, de acuerdo con lo que usted siente en ascensores de aceleración rápida frente a aceleración lenta. En la figura 6.5 (b), la lectura de la escala es $735 N$, que es igual al peso de la persona. Este es el caso siempre que el elevador tenga una velocidad constante, moviéndose hacia arriba, hacia abajo o estático.
 Comprueba tu aprendizaje 6.1
Comprueba tu aprendizaje 6.1
La solución del ejemplo anterior también se aplica a un ascensor que se acelera hacia abajo. Cuando un elevador acelera hacia abajo, $a$ es negativo, y la lectura de la escala es menor que el peso de la persona. Si se alcanza una velocidad descendente constante, la lectura de la escala vuelve a ser igual al peso de la persona. Si el elevador está en caída libre y acelera hacia abajo en $g$, entonces la lectura de la escala es cero y la persona parece no tener peso.
Ejemplo 6.4
Dos bloques unidos
La figura 6.6 muestra un bloque de masa $m_1$ en una superficie horizontal sin fricción. Se tira de una cuerda ligera que pasa sobre una polea sin masa y sin fricción.
El otro extremo de la cuerda está conectado a un bloque de masa $m_2$. Encuentra la aceleración de los bloques y la tensión en la cuerda en términos de $m_1, m_2$, y $g$.
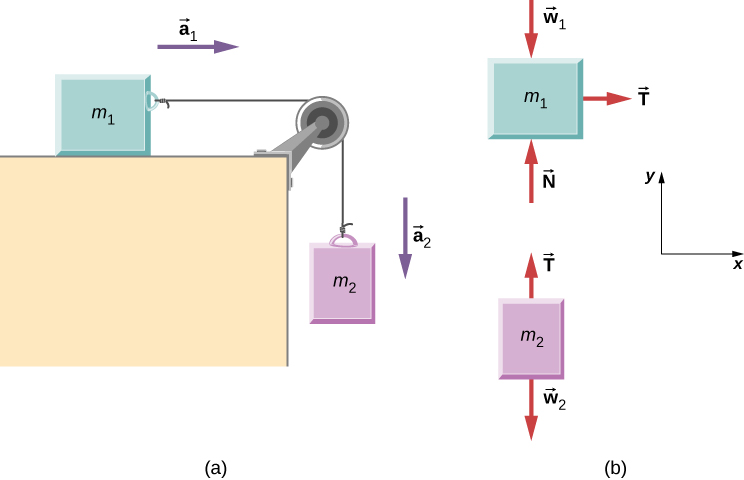
Estrategia
Dibujamos un diagrama de cuerpo libre para cada masa por separado, como se muestra en la figura 6.6.
Luego analizamos cada uno para encontrar las incógnitas requeridas. Las fuerzas en el bloque 1 son la fuerza gravitacional, la fuerza de contacto de la superficie y la tensión en la cuerda. El bloque 2 está sujeto a la fuerza gravitacional y a la tensión de la cuerda. La segunda ley de Newton se aplica a cada uno, entonces escribimos dos ecuaciones de vectores:
Para el bloque $1$: $\bold{\vec{T}} + \bold{\vec{w}}_1 + \bold{\vec{N}} = m_1\bold{\vec{a}}_1$
Para el bloque $2$: $\bold{\vec{T}} + \bold{\vec{w}}_2 = m_2\bold{\vec{a}}_2$
Observa que $\bold{\vec{T}}$ es el mismo para ambos bloques. Como la cuerda y la polea tienen una masa insignificante, y como no hay fricción en la polea, la tensión es la misma en toda la cuerda. Ahora podemos escribir ecuaciones en componentes para cada bloque. Todas las fuerzas son horizontales o verticales, por lo que podemos usar el mismo sistema de coordenadas horizontales / verticales para ambos objetos
Solución
Las ecuaciones componentes se derivan de las ecuaciones de vectores anteriores. Vemos que el bloque 1 tiene las fuerzas verticales equilibradas, por lo que las ignoramos y escribimos una ecuación que relaciona los componentes $x$. No hay fuerzas horizontales en el bloque $2$, por lo que solo se escribe la ecuación $y$. Obtenemos estos resultados:
| Bloque 1 $$\sum F_x = ma_x\\ T_x = m_1a_{1x}$$ |
Bloque 2 $$\sum F_y = ma_y\\ T_y - m_2g = m_2a_{2y}$$ |
Cuando el bloque $1$ se mueve hacia la derecha, el bloque $2$ recorre una distancia igual hacia abajo; por lo tanto, $a_{1x} = -a_{2y}$.
Escribiendo la aceleración común de los bloques como
$a = a_{1x} = -a_{2y}$, ahora tenemos
A partir de estas dos ecuaciones, podemos expresar $a$ y $T$ en términos de las masas $m_1, m_2$, y $g$:
$$a = \frac{m_2}{m_1 + m_2}g$$ $$T = \frac{m_1 m_2}{m_1 + m_2}g$$Explicación
Observa que la tensión en la cuerda es menor que el peso del bloque que cuelga del extremo. Un error común en problemas como este es establecer $T = m_2g$. Puedes ver en el diagrama de cuerpo libre del bloque $2$ que no puede ser correcto si el bloque se está acelerando.
 Comprueba tu aprendizaje 6.2
Comprueba tu aprendizaje 6.2
Ejemplo 6.5
Máquina Atwood
Un problema clásico en física, similar al que acabamos de resolver, es el de la máquina Atwood, que consiste en una cuerda que pasa sobre una polea, con dos objetos de diferente masa unidos.
Es particularmente útil para comprender la conexión entre la fuerza y el movimiento. En la figura 6.7, $m_1 = 2.00 kg$ y $m_2 = 4.00 kg$. Considera que la polea no tiene fricción. (a) Si se libera $m_2$, ¿cuál será su aceleración? (b) ¿Cuál es la tensión en la cuerda?
Estrategia
Dibujamos un diagrama de cuerpo libre para cada masa por separado, como se muestra en la figura. Luego analizamos cada diagrama para encontrar las incógnitas requeridas. Esto puede implicar la solución de ecuaciones simultáneas. También es importante tener en cuenta la similitud con el ejemplo anterior. A medida que el bloque $2$ acelera con la aceleración $a_2$ en la dirección descendente, el bloque $1$ acelera hacia arriba con la aceleración $a_1$. Por lo tanto, $a = a_1 = -a_2$.
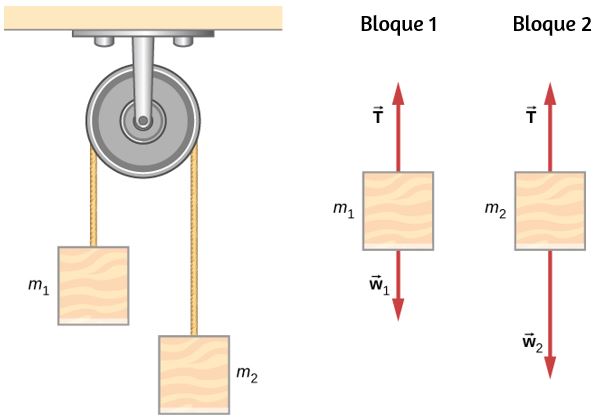
Solución
a. Tenemos.
$$\text{Para }m_1\;\;\sum F_y= T - m_1g = m_1a\\ \\ \text{Para }m_2\;\;\sum F_y = T - m_2g = -m_2a$$(El signo negativo al frente de $m_2a$ indica que $m_2$ acelera hacia abajo; ambos bloques se aceleran a la misma velocidad, pero en direcciones opuestas).
Resuelve las dos ecuaciones simultáneamente (restarlas) y el resultado es
$$(m_2 - m_1) g = (m_1 + m_2) a$$Resolviendo para $a$:
$$a = \frac{m_2 - m_1}{m_1 + m_2} = \frac{4 kg − 2 kg}{4 kg + 2 kg}(9.8 m/s^2) = 3.27 m/s^2$$b. Al observar el primer bloque, vemos que
$$T - m_1g = m_1a$$ $$T = m_1(g + a) = (2 kg)(9.8 m/s^2 + 3.27 m/s^2) = 26.1 N$$Explicación
El resultado de la aceleración dada en la solución se puede interpretar como la relación de la fuerza desequilibrada en el sistema, $(m_2 - m_1)g$, con respecto a la masa total del sistema, $m_1 + m_2$. También podemos usar la máquina Atwood para medir la fuerza del campo gravitacional local.
 Comprueba tu aprendizaje 6.3
Comprueba tu aprendizaje 6.3
Antes de continuar con este apartado, te invitamos a que practiques con dos objetos interactivos relacionados con poleas.
En el segundo objeto interactivo, tomado del repositorio de Walter Fendt, puedes elevar o bajar una carga mediante el ratón. Manteniendo el botón del ratón presionado, aparece un dinamómetro indicando la tensión en la cuerda. Se puede cambiar el peso de la carga y de las poleas colgantes en las casillas de valores correspondientes. Los datos de entrada, si son demasiado altos, se ajustan automáticamente al límite de la escala del dinamómetro ($10 N$).
Las leyes del movimiento de Newton y la cinemática
La física es más interesante y más poderosa cuando se aplica a situaciones generales que involucran más que un conjunto limitado de principios físicos.
Las leyes del movimiento de Newton también se pueden integrar con otros conceptos que se han discutido previamente en este texto para resolver problemas de movimiento. Por ejemplo, las fuerzas producen aceleraciones, un tema de cinemática y, por lo tanto, se justifica, en parte, la relevancia de capítulos anteriores.
Al abordar problemas que involucran varios tipos de fuerzas, aceleración, velocidad y / o posición, enumerar los datos y las cantidades a calcular te permitirá identificar los principios involucrados. Luego, puedes consultar los capítulos que tratan un tema en particular y resolver el problema utilizando las estrategias delineadas en el texto. El siguiente ejemplo ilustra cómo la estrategia de resolución de problemas presentada anteriormente en este capítulo, así como las estrategias presentadas en otros capítulos, se aplica a un problema conceptual integrado.
Ejemplo 6.6
¿Qué fuerza debe ejercer un jugador de fútbol para alcanzar la velocidad máxima?
Un jugador de fútbol comienza en reposo y acelera hacia adelante, alcanzando una velocidad de $8.00 m/s$ en $2.50 s$. (a) ¿Cuál es su aceleración promedio? (b) ¿Qué fuerza promedio ejerce la tierra hacia adelante sobre el corredor para que logre esta aceleración? La masa del jugador es de $70.0 kg$, y la resistencia del aire es insignificante.
Estrategia
Para encontrar las respuestas a este problema, usamos la estrategia de resolución de problemas dada anteriormente en este capítulo. Las soluciones para cada parte del ejemplo ilustran cómo aplicar pasos específicos de resolución de problemas.
En este caso, no necesitamos usar todos los pasos. Simplemente identificamos los principios físicos, y por lo tanto los datos conocidos y las incógnitas; aplicar la segunda ley de Newton; y verificar si la respuesta es razonable.
Solución
a. Se nos dan las velocidades inicial y final (cero y $8.00 m/s$ hacia adelante); por lo tanto, el cambio en la velocidad es $\Delta v = 8.00 m/s$. Nos dan el tiempo transcurrido, entonces $\Delta t = 2.50 s$. La incognita es la aceleración, que se puede encontrar a partir de su definición:
$$a = \frac{\Delta v}{\Delta t}$$Sustituyendo los valores conocidos
$$a = \frac{8.00 m/s}{2.50 s} = 3.20 m/s^2$$b. Aquí se nos pide que descubramos la fuerza promedio que ejerce el suelo sobre el corredor para producir esta aceleración (Recuerda que estamos tratando con la fuerza o fuerzas que actúan sobre el objeto de interés).
Esta es la fuerza de reacción a la ejercida por el jugador hacia atrás contra el suelo, por la tercera ley de Newton. Despreciando la resistencia del aire, esto sería igual en magnitud a la fuerza externa neta en el jugador, ya que esta fuerza causa su aceleración. Como ahora sabemos la aceleración del jugador y se nos da su masa, podemos usar la segunda ley de Newton para encontrar la fuerza ejercida. Es decir,
$$\bold{\vec{F}}_{Neta} = ma$$Sustituyendo los valores conocidos de $m$ y $a$, obtenemos
$$\bold{\vec{F}}_{Neta} = (70.0 kg)(3.20 m/s^2) = 224 N$$Este es un resultado razonable: la aceleración es alcanzable para un atleta en buenas condiciones. La fuerza es de aproximadamente $50$ libras, una fuerza promedio razonable.
Explicación
Este ejemplo ilustra cómo aplicar estrategias de resolución de problemas a situaciones que incluyen temas de diferentes capítulos. El primer paso es identificar los principios físicos, los datos conocidos y las incógnitas involucradas en el problema. El segundo paso es hallar la o las incognitas, en este caso usando la segunda ley de Newton. Finalmente, verificamos nuestra respuesta para asegurarnos de que sea razonable. Estas técnicas para problemas conceptuales integrados serán útiles en aplicaciones de la física fuera de un curso de física, como en tu profesión, en otras disciplinas científicas y en la vida cotidiana.
 Comprueba tu aprendizaje 6.4
Comprueba tu aprendizaje 6.4
Ejemplo 6.7
¿Qué fuerzas actúan en un helicóptero modelo?
Un helicóptero modelo de $1.50 kg$ tiene una velocidad de $5.0\^{\bold{j}} m/s$ en $t = 0$. Se acelera a una velocidad constante durante dos segundos ($2,00 s$) después de lo cual tiene una velocidad de $(6.00\^{\bold{i}} + 12.00\^{\bold{j}}) m/s$. ¿Cuál es la magnitud de la fuerza resultante que actúa sobre el helicóptero durante este intervalo de tiempo?
Estrategia
Podemos configurar fácilmente un sistema de coordenadas en el que el eje $x$ (dirección $\^{\bold{i}}$) es horizontal, $y$ el eje y (dirección $\^{\bold{j}}$) es vertical. Sabemos que $\Delta t = 2.00 s$ y $\Delta v = (6.00\^{\bold{i}} + 12.00\^{\bold{j}}) m/s - (5.00\^{\bold{j}} m/s)$. A partir de esta información, podemos calcular la aceleración según la definición ; entonces podemos aplicar la segunda ley de Newton.
Solución
Tenemos
$$\begin{split} a &= \frac{\Delta v}{\Delta t}= \frac{(6.00\^{\bold{i}} + 12.00\^{\bold{j}}) m/s - (5.00\^{\bold{j}} m/s)}{2.00 s}\\ &= 3.00\^{\bold{i}} + 3.50\^{\bold{j}} m/s^2\\ \end{split}$$ $$\sum \bold{\vec{F}} = m\bold{\vec{a}} = (1.50 kg)(3.00\^{\bold{i}} + 3.50\^{\bold{j}} m/s^2) = 4.50\^{\bold{i}} + 5.25\^{\bold{j}} N$$La magnitud de la fuerza se calcula fácilmente:
$$F = \sqrt{(4.50 N)^2 + (5.25 N)^2} = 6.91 N$$Explicación
El problema original se estableció en términos de los componentes rectangulares $\^{\bold{i}}$ y $\^{\bold{j}}$, por lo que utilizamos métodos vectoriales. Compara este ejemplo con el ejemplo anterior.
 Comprueba tu aprendizaje 6.5
Comprueba tu aprendizaje 6.5
Ejemplo 6.8
Tractor de equipaje
La figura 6.8 (a) muestra un tractor de equipaje que saca los carros de equipaje de un avión. El tractor tiene una masa de $650.0 kg$, mientras que el carro $A$ tiene una masa de $250.0 kg$ y el carro $B$ tiene una masa de $150.0 kg$. La fuerza impulsora que actúa durante un breve período de tiempo acelera el sistema desde el reposo y actúa durante $3.00 s$. (a) Si esta fuerza motriz está dada por $F = (820.0t) N$, encuentra la velocidad después de $3.00$ segundos. (b) ¿Cuál es la fuerza horizontal que actúa sobre el cable de conexión entre el tractor y el carro A en este momento?
Estrategia
Un diagrama de cuerpo libre muestra la fuerza motriz del tractor, que le da al sistema su aceleración. Solo tenemos que considerar el movimiento en la dirección horizontal.
Las fuerzas verticales se equilibran entre sí y no es necesario considerarlas. Para la parte b, hacemos uso de un diagrama de cuerpo libre del tractor solo para determinar la fuerza entre él y el carrito $A$. Esto expone la fuerza de enganche $\bold{\vec{T}}$, que es nuestro objetivo.
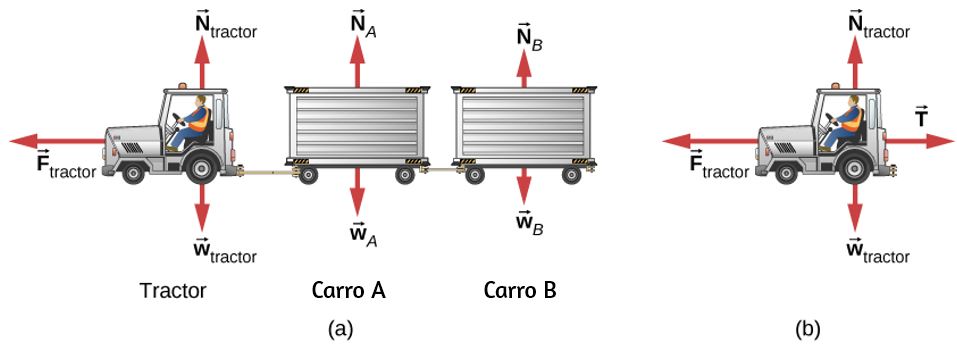
Solución
a. $\displaystyle\sum F_x = m_{sistema}a_x y \sum F_x = 820.0t$, entonces: $$820.0 t = (650.0 +250.0 + 150.0)a\\ a = 0.7809t$$Como la aceleración es una función del tiempo, podemos determinar la velocidad del tractor usando $a = \frac{dv}{dt}$ con la condición inicial que $v_0 = 0$ en $t = 0$. Integramos desde $t = 0$ hasta $t = 3$:
$$dv = adt, \int_0^3 dv = \int_0^3 adt =\int_0^3 0.7809dt = 0.3905t^2\Big]_0^3 = 3.51 m/s$$b. Consulta el diagrama de cuerpo libre en la figura 6.8(b).
$$\sum F_x = m_{tractor}a_x\\ 820.0t - T = m_{tractor}(0.7805)t\\ (820.0)(3.00) − T = (650.0)(0.7805)(3.00)\\ T = 938 N$$Explicación
Dado que la fuerza varía con el tiempo, debemos usar el cálculo para resolver este problema. Observa cómo la masa total del sistema fue importante para resolver la figura 6.8 (a), mientras que solo la masa del camión (dado que suministró la fuerza) era útil en la figura 6.8 (b).
Recuerda que $v = \frac{ds}{dt}$ y $a = \frac{dv}{dt}$. Si la aceleración es una función del tiempo, podemos usar las fórmulas de cálculo desarrolladas en el capítulo de cinemática, como se muestra en este ejemplo. Sin embargo, a veces la aceleración es una función del desplazamiento. En este caso, podemos derivar un resultado importante de estas relaciones de cálculo. Resolviendo para dt en cada uno, tenemos $dt = \frac{ds}{v}$ y $dt = \frac{dv}{a}$. Ahora, equiparando estas expresiones, tenemos $\frac{ds}{v} = \frac{dv}{a}$. Podemos reorganizar esto para obtener $ads = vdv$.
Ejemplo 6.9
Movimiento de un proyectil disparado verticalmente
Una granada de mortero de $10.0 kg$ se dispara verticalmente hacia arriba desde el suelo, con una velocidad inicial de $50.0 m/s$ (ver la figura 6.9).
Determina la altura máxima que recorrerá si la resistencia atmosférica se mide como $F_D = (0.0100v^2) N$, donde $v$ es la velocidad en cualquier instante.
Estrategia
La fuerza conocida en el caparazón del mortero puede estar relacionada con su aceleración, usando las ecuaciones de movimiento. La cinemática se puede usar para relacionar la aceleración de la caparazón de mortero con su posición.

Solución
Inicialmente, $y_0 = 0$ y $v_0 = 50.0 m/s$. En la altura máxima $y = h, v = 0$. El diagrama de cuerpo libre muestra que $F_D actúa hacia abajo, porque ralentiza el movimiento ascendente del caparazón de mortero. Por lo tanto, podemos escribir
$$F_y = ma_y\\ −F_y − w = ma_y\\ −0.0100v^2 − 98.0 = 10.0a\\ a = −0.00100v^2 − 9.80$$La aceleración depende de $v$ y, por lo tanto, es variable. Como $a = f(v)$, podemos relacionar $a$ y $v$ usando la reordenación descrita anteriormente,
$$ads = vdv$$Reemplazamos $ds$ por $dy$ porque estamos tratando con la dirección vertical,
$$ady = vdv, (-0.00100v^2 - 9.80)dy = vdv$$Ahora separamos las variables ($v's$ y $dv's$ en un lado; $dy$ en el otro):
$$\begin{split} \int_0^h dy &= \int_{50.0}^0\frac{vdv}{(−0.00100v^2 − 9.80)}\\ &= - \int_{50.0}^0\frac{vdv}{(0.00100v^2 + 9.80)}\\ &= (-5 \times 10^3)ln(0.00100v^2 + 9.80)\Big]_0^{50.0}\\ \end{split}$$Luego, $h = 114m$.
Explicación
Observa la necesidad de aplicar el cálculo ya que la fuerza no es constante, lo que también significa que la aceleración no es constante. Para empeorar las cosas, la fuerza depende de $v$ (no $t$), por lo que debemos usar el truco explicado antes del ejemplo. La respuesta para la altura indica una elevación más baja si hubo resistencia al aire. Trataremos los efectos de la resistencia del aire y otras fuerzas de arrastre con mayor detalle en el apartado de Fuerza de arrastre y Velocidad terminal.
 Comprueba tu aprendizaje 6.6
Comprueba tu aprendizaje 6.6
Fricción
Cuando un cuerpo está en movimiento, tiene resistencia porque el cuerpo interactúa con su entorno. Esta resistencia es una fuerza de fricción. La fricción se opone al movimiento relativo entre los sistemas en contacto, pero también nos permite movernos, un concepto que se vuelve obvio si tratas de caminar sobre el hielo. La fricción es una fuerza común pero compleja, y su comportamiento todavía no se comprende por completo. Aún así, es posible entender las circunstancias en las que se comporta.
Fricción estática y cinética
La definición básica de fricción es relativamente simple de declarar.
La fricción es una fuerza que se opone al movimiento relativo entre sistemas en contacto.
Hay varias formas de fricción. Una de las características más simples de la fricción deslizante es que es paralela a las superficies de contacto entre los sistemas y siempre está en una dirección que se opone al movimiento o al intento de movimiento de los sistemas entre sí. Si dos sistemas están en contacto y se mueven entre sí, entonces la fricción entre ellos se denomina fricción cinética. Por ejemplo, la fricción ralentiza un disco de hockey deslizándose sobre hielo. Cuando los objetos están estáticos, la fricción estática puede actuar entre ellos; la fricción estática suele ser mayor que la fricción cinética entre dos objetos.
Si dos sistemas están en contacto y estáticos entre sí, entonces la fricción entre ellos se llama fricción estática. Si dos sistemas están en contacto y se mueven entre sí, entonces la fricción entre ellos se denomina fricción cinética.
Imagina, por ejemplo, tratar de deslizar una caja pesada sobre un piso de concreto; puedes empujar con fuerza sobre la caja y no moverla en absoluto. Esto significa que la fricción estática responde a lo que haces: aumenta para ser igual y en la dirección opuesta a la de tu empuje. Si finalmente empujas con fuerza, la caja parece resbalar de repente y comienza a moverse.
Ahora la fricción estática da paso a la fricción cinética. Una vez en movimiento, es más fácil mantenerlo, lo que indica que la fuerza de fricción cinética es menor que la fuerza de fricción estática. Si agregas masa a la caja, por ejemplo colocando una caja encima, debes empujar aún más para que comience y mantenerla en movimiento. Además, si aceitas el concreto, te resultaría más fácil empujar la caja (como era de esperar).
La figura 6.10 es una representación gráfica de cómo se produce la fricción en la interfaz entre dos objetos. La inspección de cerca de estas superficies muestra que son ásperas. Por lo tanto, cuando empujas para que un objeto se mueva (en este caso, una caja), debes levantar el objeto hasta que pueda saltar junto con las aristas de la superficie que golpean, rompiéndolas.
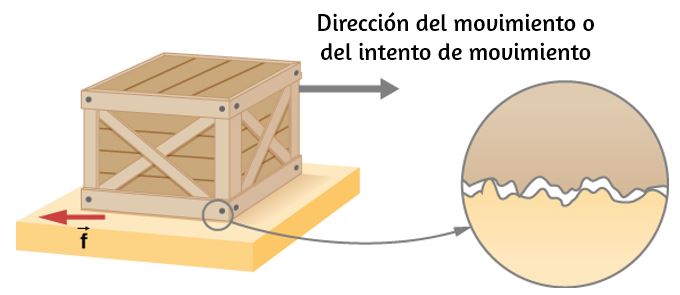
Una fuerza considerable puede ser resistida por la fricción sin movimiento aparente. Cuanto más se junten las superficies (por ejemplo, si se coloca otra caja encima), más fuerza se necesita para moverlas.
Parte de la fricción se debe a las fuerzas adhesivas entre las moléculas de superficie de los dos objetos, lo que explica la dependencia de la fricción de la naturaleza de las sustancias. Por ejemplo, los zapatos con suela de goma se deslizan menos que los que tienen suela de cuero. La adherencia varía con las sustancias en contacto y es un aspecto complicado de la física de la superficie. Una vez que un objeto se está moviendo, hay menos puntos de contacto (menos moléculas se adhieren), por lo que se requiere menos fuerza para mantener el objeto en movimiento. A velocidades pequeñas pero distintas de cero, la fricción es casi independiente de la velocidad.
La magnitud de la fuerza de fricción tiene dos formas: una para situaciones estáticas (fricción estática) y la otra para situaciones que implican movimiento (fricción cinética). Lo que sigue es un modelo empírico aproximado (determinado experimentalmente). Estas ecuaciones para la fricción estática y cinética no son ecuaciones vectoriales.
La magnitud de la fricción estática $f_s$ es $$f_s \le \mu_sN\tag{6.1}$$ donde $\mu_s$ es el coeficiente de fricción estática y $N$ es la magnitud de la fuerza normal.
El símbolo $\le$ significa menor o igual a, lo que implica que la fricción estática puede tener un valor máximo de $\mu_sN$. La fricción estática es una fuerza sensible que aumenta para ser igual y opuesta a cualquier fuerza que se ejerza, hasta su límite máximo. Una vez que la fuerza aplicada excede $f_s(max)$, el objeto se mueve. Así,
$$f_s(max) = \mu_sN$$La magnitud de la fricción cinética $f_k$ está dada por $$f_k =\mu_kN\tag{6.2}$$ donde $\mu_k$ es el coeficiente de fricción cinética.
Un sistema en el que $f_k = \mu_kN$ se describe como un sistema en el cual la fricción se comporta de manera simple. La transición de la fricción estática a la fricción cinética se ilustra en la figura 6.11.
Las ecuaciones 6.1 y 6.2 incluyen la dependencia de la fricción de los materiales y de la fuerza normal. La dirección de la fricción es siempre opuesta a la del movimiento, paralela a la superficie entre los objetos y perpendicular a la fuerza normal. Por ejemplo, si la caja que intentas empujar (con una fuerza paralela al piso) tiene una masa de $100 kg$, entonces la fuerza normal es igual a su peso,
$$w = mg = (100 kg)(9.80 m / s^2) = 980N,$$perpendicular al piso. Si el coeficiente de fricción estática es $0.45$, deberías ejercer una fuerza paralela al piso mayor que
para mover la caja. Una vez que hay movimiento, la fricción es menor y el coeficiente de fricción cinética puede ser $0.30$, por lo que una fuerza de solo
$$f_k = \mu_kN = (0.30)(980N) = 290N$$lo mantiene en movimiento a una velocidad constante. Si el suelo está lubricado, ambos coeficientes son considerablemente menores de lo que serían sin lubricación. El coeficiente de fricción es una cantidad sin unidades con una magnitud generalmente entre $0$ y $1.0$. El valor real depende de las dos superficies que están en contacto.
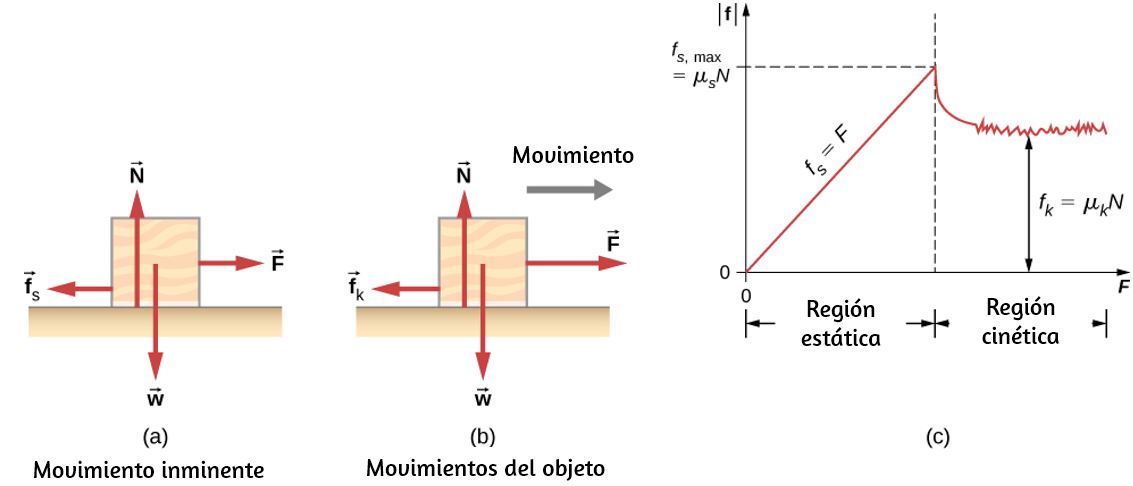
Como puedes ver en la Tabla 6.1, los coeficientes de fricción cinética son menores que sus contrapartes estáticas. Los valores aproximados de μ se indican con solo uno o dos dígitos para indicar la descripción aproximada de la fricción dada por las dos ecuaciones anteriores.
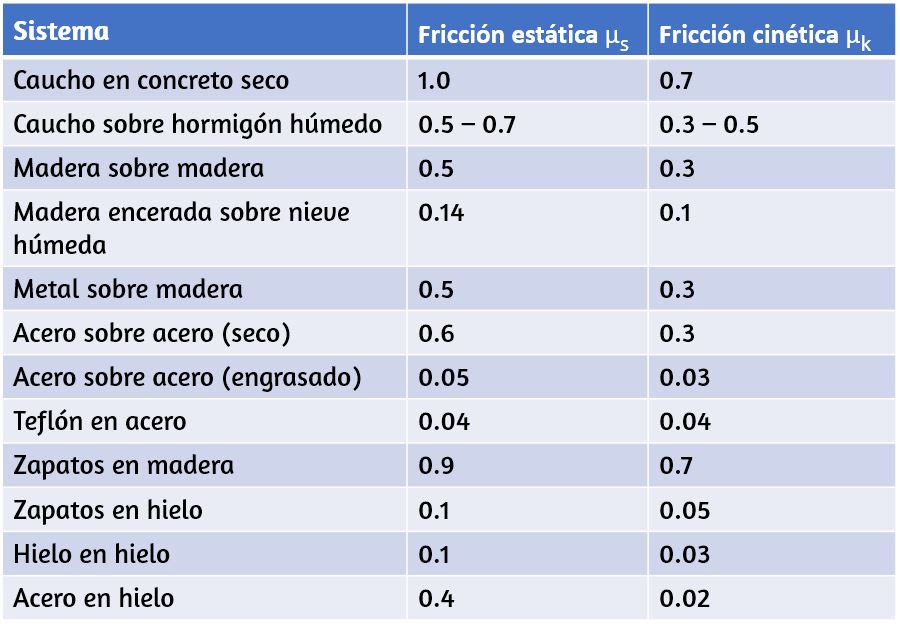
Muchas personas han experimentado el deslizamiento al caminar sobre hielo. Sin embargo, muchas partes del cuerpo, especialmente las articulaciones, tienen coeficientes de fricción mucho más pequeños, a menudo tres o cuatro veces menos que el hielo.
Una articulación está formada por los extremos de dos huesos, que están conectados por tejidos gruesos. La articulación de la rodilla está formada por el hueso de la parte inferior de la pierna (la tibia) y el fémur.
La cadera es una articulación esférica (al final del fémur) y un alvéolo (parte de la pelvis). Los extremos de los huesos de la articulación están cubiertos por cartílago, que proporciona una superficie lisa y casi vidriosa. Las articulaciones también producen un fluido (líquido sinovial) que reduce la fricción y el desgaste. Una articulación dañada o artrítica puede reemplazarse por una articulación artificial (Figura 6.12). Estos reemplazos pueden estar hechos de metales (acero inoxidable o titanio) o plástico (polietileno), también con coeficientes de fricción muy pequeños.
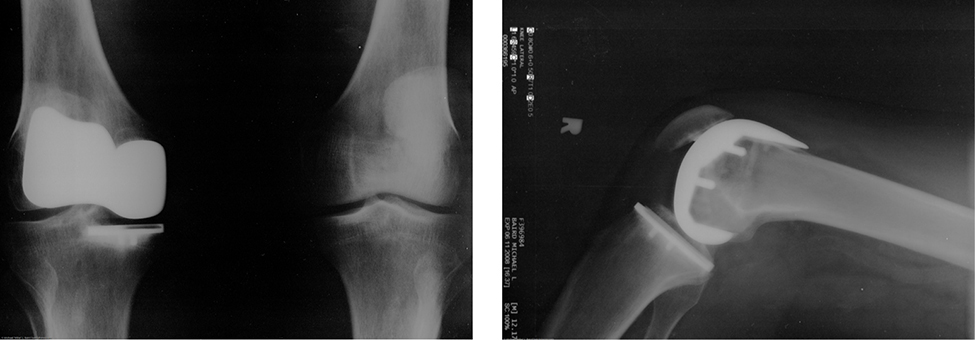
Los lubricantes naturales incluyen la saliva producida en la boca para ayudar en el proceso de deglución, y la mucosidad resbaladiza que se encuentra entre los órganos del cuerpo, lo que les permite moverse libremente unos a otros durante los latidos del corazón, durante la respiración y cuando una persona se mueve.
Los hospitales y clínicas generalmente usan lubricantes artificiales, como geles, para reducir la fricción.
Las ecuaciones dadas para la fricción estática y cinética son leyes empíricas que describen el comportamiento de las fuerzas de fricción. Si bien estas fórmulas son muy útiles para fines prácticos, no tienen el estado de enunciados matemáticos que representan principios generales (por ejemplo, la segunda ley de Newton). De hecho, hay casos para los que estas ecuaciones ni siquiera son buenas aproximaciones. Por ejemplo, ninguna de las fórmulas es precisa para superficies lubricadas o para dos superficies que se colocan una sobre otra a altas velocidades. A menos que se especifique, no nos preocuparemos por estas excepciones.
Ejemplo 6.10
Fricción estática y cinética
Una caja de $20.0 kg$ está en reposo en un piso como se muestra en la Figura 6.13. El coeficiente de fricción estática entre la caja y el piso es 0.700 y el coeficiente de fricción cinética es 0.600. Una fuerza horizontal $\bold{\vec{P}}$ se aplica a la caja. Encuentra la fuerza de fricción si (a) $P = 20.0 N$, (b) $P = 30.0 N$, (c) $P = 120.0 N$, y (d) $P = 180.0 N$.
Estrategia
El diagrama de cuerpo libre de la caja se muestra en la figura 6.13 (b). Aplicamos la segunda ley de Newton en las direcciones horizontal y vertical, incluida la fuerza de fricción en oposición a la dirección del movimiento de la caja.
Solución
Usando la segunda ley de Newton, obtenemos:
$$F_x = ma_x\;\;\;\;\;F_y = ma_y$$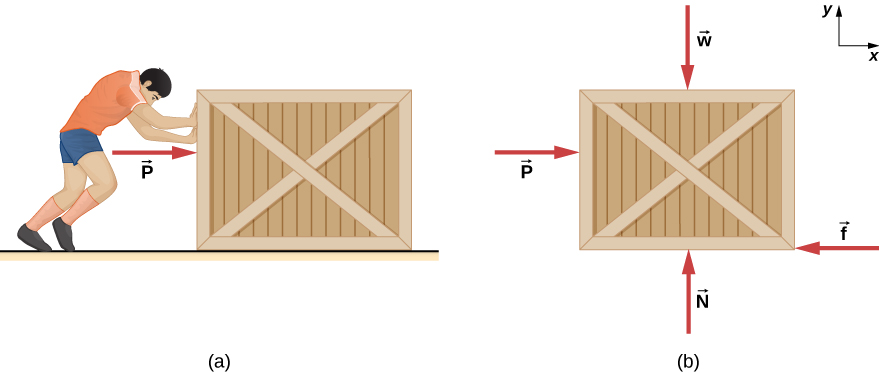
Aquí estamos usando el símbolo f para representar la fuerza de fricción ya que aún no hemos determinado si la caja está sujeta a la fricción estática o la fricción cinética. Hacemos esto cuando no estamos seguros de qué tipo de fricción está actuando. Ahora el peso de la caja es
$$w = (20.0 kg)(9.80 m/s^2) = 196 N$$que también es igual a $N$. La fuerza máxima de fricción estática es por lo tanto $(0.700)(196 N) = 137 N$. Siempre que $P$ sea menor que $137 N$, la fuerza de fricción estática mantiene la caja estacionaria y $f_s = P$. Por lo tanto, (a) $f_s = 20.0 N$, (b) $f_s = 30.0 N$, y (c) $f_s = 120.0 N$.
(d) Si $P = 180.0 N$, la fuerza aplicada es mayor que la fuerza máxima de fricción estática $(137 N)$, por lo que la caja ya no puede
permanecer en reposo. Una vez que la caja está en movimiento, actúa la fricción cinética. Entonces
$$f_k = \mu_kN = (0.600)(196 N) = 118N$$y la aceleración es
$$a_x = \frac{P - f_k}{m} =\frac{180.0 N − 118 N}{20.0 kg} = 3.10 m/s^2$$Explicación
Este ejemplo ilustra cómo consideramos la fricción en un problema de dinámica. Observa que la fricción estática tiene un valor que coincide con la fuerza aplicada, hasta que alcanzamos el valor máximo de fricción estática. Además, no puede ocurrir movimiento hasta que la fuerza aplicada sea igual a la fuerza de fricción estática, pero la fuerza de la fricción cinética se volverá más pequeña.
 Comprueba tu aprendizaje 6.7
Comprueba tu aprendizaje 6.7
Fricción y el plano inclinado
Una situación donde la fricción juega un papel obvio es la de un objeto en una pendiente. Puede ser una caja que se empuja por una rampa hasta un muelle de carga o un skater que desciende por una montaña, pero la física básica es la misma.
Usualmente generalizamos la superficie inclinada y la llamamos un plano inclinado. Veamos un ejemplo de análisis de movimiento en un plano inclinado con fricción.
Ejemplo 6.11
Esquiador cuesta abajo
Un esquiador con una masa de 62 kg se desliza por una pendiente nevada a una velocidad constante. Encuentra el coeficiente de fricción cinética para el esquiador si se sabe que la fricción es $45.0 N$.

Estrategia
La magnitud de la fricción cinética se da como $45.0 N$. La fricción cinética está relacionada con la fuerza normal $N$ por $f_k = \mu_kN$; por lo tanto, podemos encontrar el coeficiente de fricción cinética si podemos encontrar la fuerza normal en el esquiador.
La fuerza normal es siempre perpendicular a la superficie, y como no hay movimiento perpendicular a la superficie, la fuerza normal debe ser igual al componente del peso del esquiador perpendicular a la pendiente. (Véase la figura 6.14, que repite una figura del capítulo sobre las leyes del movimiento de Newton).
Tenemos
$$N = w_y = wcos25\degree = mgcos25\degree$$Sustituyendo en la expresión de fricción cinética, obtenemos
$$f_k =\mu_kmgcos25\degree$$que ahora puede ser resuelto por el coeficiente de fricción cinética $\mu_k$.
Solución
La solución para $\mu_k$ da
$$\mu_k = \frac{f_k}{N} = \frac{f_k}{wcos25\degree} = \frac{f_k}{mgcos25\degree}$$Sustituyendo los valores conocidos en el lado derecho de la ecuación,
$$\mu_k = \frac{45.0 N}{(62 kg)(9.80 m/s^2)(0.906)} = 0.082$$Explicación
Este resultado es un poco más pequeño que el coeficiente enumerado en la Tabla 6.1 para madera encerada en nieve, pero aún es razonable ya que los valores de los coeficientes de fricción pueden variar mucho. En situaciones como esta, donde un objeto de masa $m$ se desliza por una pendiente que forma un ángulo $\theta$ con la horizontal, la fricción viene dada por $f_k = \mu_kmgcos\theta$. Todos los objetos se deslizan por una pendiente con aceleración constante bajo estas circunstancias.
Hemos discutido que cuando un objeto descansa sobre una superficie horizontal, la fuerza normal que lo soporta es igual en magnitud a su peso. Además, la fricción simple siempre es proporcional a la fuerza normal. Cuando un objeto no está sobre una superficie horizontal, como ocurre con el plano inclinado, debemos encontrar la fuerza que actúa sobre el objeto que se dirige perpendicularmente a la superficie; que es un componente del peso.
Ahora derivamos una relación útil para calcular el coeficiente de fricción en un plano inclinado. Ten en cuenta que el resultado se aplica solo a situaciones en las que el objeto se desliza a velocidad constante por la rampa.
Un objeto se desliza por un plano inclinado a una velocidad constante si la fuerza neta en el objeto es cero. Podemos usar este hecho para medir el coeficiente de fricción cinética entre dos objetos. Como se muestra en el ejemplo 6.10, la fricción cinética en una pendiente es $f_k = \mu_kmgcos\theta$. La componente del peso en la pendiente es igual a $mgsen\theta$ (ver el diagrama de cuerpo libre en la figura 6.14). Estas fuerzas actúan en direcciones opuestas, por lo que cuando tienen la misma magnitud, la aceleración es cero. Escribiendo esto,
$$\mu_kmgcos\theta = mgsen\theta$$Resolviendo para $\mu_k$, encontramos que
$$\mu_k = \frac{mgsen\theta}{mgcos\theta} = tan\theta$$Pon una moneda en un libro e inclínalo hasta que la moneda se deslice a una velocidad constante por el libro.
Es posible que deba tocar ligeramente el libro para que la moneda se mueva. Mide el ángulo de inclinación relativo a la horizontal y encuentre $\mu_k$. Ten en cuenta que la moneda no comienza a deslizarse en absoluto hasta que se alcanza un ángulo mayor que θ, ya que el coeficiente de fricción estática es mayor que el coeficiente de fricción cinética. Piensa en cómo esto puede afectar el valor de $\mu_k$.
Explicaciones de fricción a escala atómica
Los aspectos más simples de la fricción tratados hasta ahora son sus características macroscópicas (a gran escala). Se han dado grandes pasos en la explicación de la fricción a escala atómica durante las últimas décadas. Los investigadores están descubriendo que la naturaleza atómica de la fricción parece tener varias características fundamentales. Estas características no solo explican algunos de los aspectos más simples de la fricción, también tienen el potencial para el desarrollo de entornos libres de fricción que podrían ahorrar cientos de miles de millones de dólares en energía que actualmente se está convirtiendo (innecesariamente) en calor.
La figura 6.15 ilustra una característica macroscópica de la fricción que se explica por la investigación microscópica (a pequeña escala). Hemos notado que la fricción es proporcional a la fuerza normal, pero no a la cantidad de área en contacto, una noción algo contra intuitiva.
Cuando dos superficies ásperas están en contacto, el área de contacto real es una pequeña fracción del área total porque solo tocan los puntos altos de sus aristas o rugosidades. Cuando se ejerce una fuerza normal mayor, el área de contacto real aumenta, y encontramos que la fricción es proporcional a esta área.
Sin embargo, la vista a escala atómica promete explicar mucho más que las características más simples de la fricción. El mecanismo de cómo se genera el calor ahora se está determinando. En otras palabras, ¿por qué las superficies se calientan más cuando se frotan?
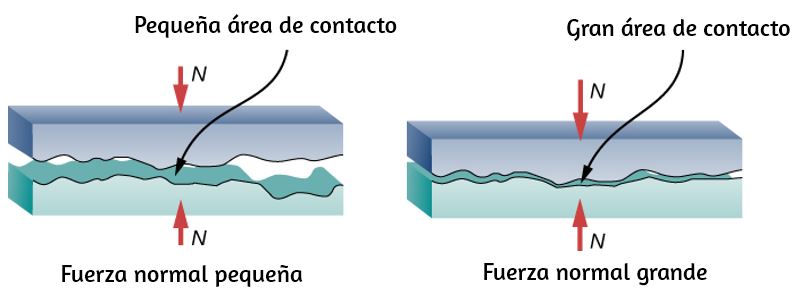
Esencialmente, los átomos están vinculados entre sí para formar redes.
Cuando las superficies se frotan, los átomos de la superficie se adhieren y hacen que las redes atómicas vibren, creando esencialmente ondas de sonido que penetran en el material. Las ondas de sonido disminuyen con la distancia, y su energía se convierte en calor. Las reacciones químicas que están relacionadas con el desgaste por fricción también pueden ocurrir entre átomos y moléculas en las superficies.
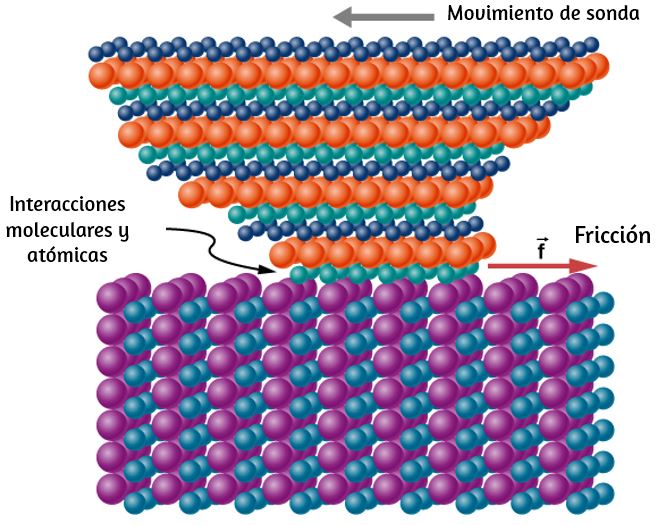
En el siguiente objeto interactivo, observa cómo la fricción causa que un material se caliente y se funda ¿Qué pasa a nivel atómico cuando se frotan dos objetos entre sí? Describe un modelo de fricción a nivel molecular, la materia en términos de movimiento molecular. La descripción debe incluir: esquemas de apoyo a la descripción, cómo la temperatura afecta la imagen, cuáles son las diferencias y similitudes entre el movimiento de partículas de los sólidos, líquidos y gases; cómo el tamaño y la velocidad de las moléculas de gas se relacionan con los objetos cotidianos.
Ejemplo 6.12
Bloques deslizantes
Los dos bloques de la figura 6.17 están unidos entre sí por una cuerda sin masa que está envuelta alrededor de una polea sin fricción. Cuando el bloque inferior de $4.00 kg$ es empujado hacia la izquierda por la fuerza constante $\bold{\vec{P}}$, el bloque superior de $2.00 kg$ se desliza hacia la derecha. Encuentra la magnitud de la fuerza necesaria para mover los bloques a velocidad constante. Supó que el coeficiente de fricción cinética entre todas las superficies es $0.400$.
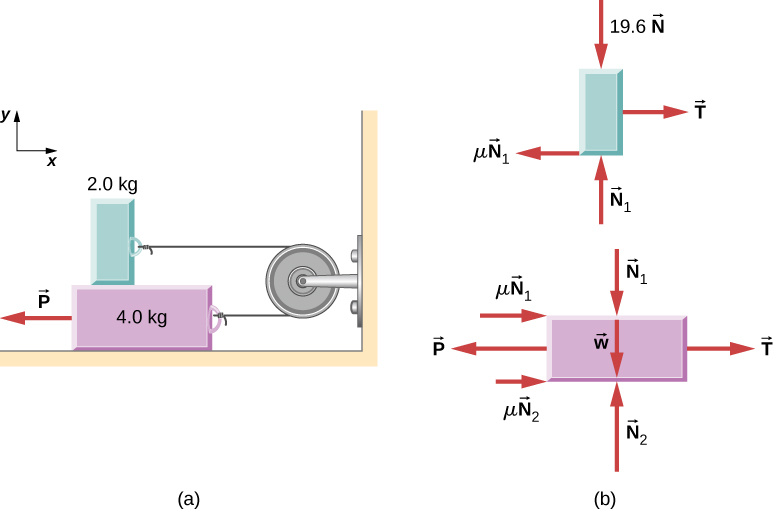
Estrategia
Analizamos los movimientos de los dos bloques por separado. El bloque superior está sujeto a una fuerza de contacto ejercida por el bloque inferior. Los componentes de esta fuerza son la fuerza normal $N_1$ . Otras fuerzas en el bloque superior son la tensión $T_i$ en la cuerda y el peso del propio bloque superior, $19.6 N$. El bloque inferior está sometido a fuerzas de contacto debido al bloque superior y al piso. La primera fuerza de contacto tiene componentes $-N_1$ y $0.400N_1$ , que son simplemente fuerzas de reacción a las fuerzas de contacto que ejerce el bloque inferior en el bloque superior. Las componentes de la fuerza de contacto del piso son $N_2$ y $0.400N_2$. Otras fuerzas en este bloque son $-P$, la tensión $T_i$ y el peso $-39.2 N$.
Solución
Como el bloque superior se mueve horizontalmente hacia la derecha a velocidad constante, su aceleración es cero tanto en la dirección horizontal como en la vertical. De la segunda ley de Newton,
$$\sum F_x = m_1a_x\;\;\;\;\; \sum F_y = m_1a_y$$ $$T - 0.400N_1 = 0\;\;\;\;\;N_1 -19.6 N = 0$$Resolviendo para las dos incógnitas, obtenemos $N_1 = 19.6N$ y $T = 0.40N_1 = 7.84 N$. El bloque inferior tampoco se está acelerando, por lo que la aplicación de la segunda ley de Newton a este bloque da
$$\sum F_x = m_2a_x \;\;\;\;\; \sum F_y = m_2a_y$$ $$T - P + 0.400N_1 + 0.400N_2 = 0 \;\;\;\;\;N_2 -39.2 N - N_1 = 0$$Los valores de $N_1$ y $T$ se encontraron con el primer conjunto de ecuaciones. Sustituyendo en el segundo conjunto de ecuaciones, podemos determinar $N_2$ y $P$, así:
$$N_2 = 58.8N$\;\;\;\text{y}\;\;\; P = 39.2 N$$Explicación
Comprender en qué dirección dibujar la fuerza de fricción suele ser problemático. Observa que cada fuerza de fricción etiquetada en la figura 6.17 actúa en la dirección opuesta al movimiento de su bloque correspondiente.
Ejemplo 6.13
Una caja en un camión acelerado
Una caja de $50.0 kg$ descansa sobre la plataforma de un camión como se muestra en la figura 6.18. Los coeficientes de fricción entre las superficies son $\mu_k = 0.30$ y $\mu_s = 0.400$. Encuentra la fuerza de fricción en la caja cuando la carretilla está acelerando hacia adelante en relación con el suelo a (a) $2.00 m/s^2$, y (b) a $5.00 m/s^2$.
Estrategia
Las fuerzas en la caja son su peso y las fuerzas normales y de fricción debidas al contacto con la plataforma del camión. Comenzamos por asumir que la caja no se está deslizando. En este caso, la fuerza de fricción estática $f_2$ actúa sobre la caja. Además, las aceleraciones de la caja y el camión son iguales.
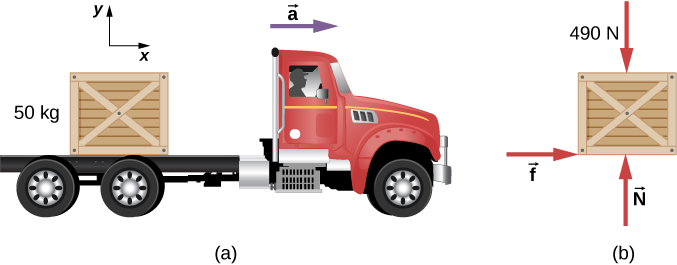
Solución
De la aplicación de la segunda ley de Newton a la caja, usando el marco de referencia unido al suelo, resulta
$$\sum F_x = ma_x \;\;\,\;\;\sum F_y = ma_y$$ $$f_s = (50.0 kg)(2.00 m/s^2) \;\;\,N − 4.90 \times 10^2 N = (50.0kg)(0)$$ $$f_s = 1.00 \times 10^2 N \;\;\;\;\; N = 4.90 \times 10^2 N$$Ahora podemos verificar la validez de nuestra suposición de no deslizamiento. El valor máximo de la fuerza de fricción estática es
$$\mu_sN = (0.400)(4.90 \times 10^2 N) = 196 N$$Como esto excede el máximo de $196 N$, la caja debe deslizarse. La fuerza de fricción es por lo tanto cinética y es
$$f_k = \mu_kN = (0.300)(4.90 \times 10^2 N) = 147 N$$La aceleración horizontal de la caja en relación con el suelo ahora se encuentra a partir de
$$\sum F_x = m_x$$ $$147 N = (50.0 kg)a_x$$ $$a_x = 2.94 m/s^2$$Explicación
En relación con el suelo, el camión está acelerando hacia adelante a $5,0 m/s^2$ y la caja está acelerando hacia adelante a $2.94 m/s^2$. Por lo tanto, la caja se desliza hacia atrás en relación con la plataforma del camión con una aceleración de $2.94 m/s^2 - 5.00 m/s^2 = -2.06 m/s^2$.
Ejemplo 6.14
Esquiando
Anteriormente, analizamos la situación de un esquiador cuesta abajo moviéndose a velocidad constante para determinar el coeficiente de fricción cinética.
Ahora hagamos un análisis similar para determinar la aceleración. El esquiador de la figura 6.19 se desliza por una pendiente inclinada a $\theta = 13\degree$ con la horizontal. El coeficiente de fricción cinética entre el tablero y la nieve es$\mu_k = 0.20$. ¿Cuál es la aceleración del esquiador?
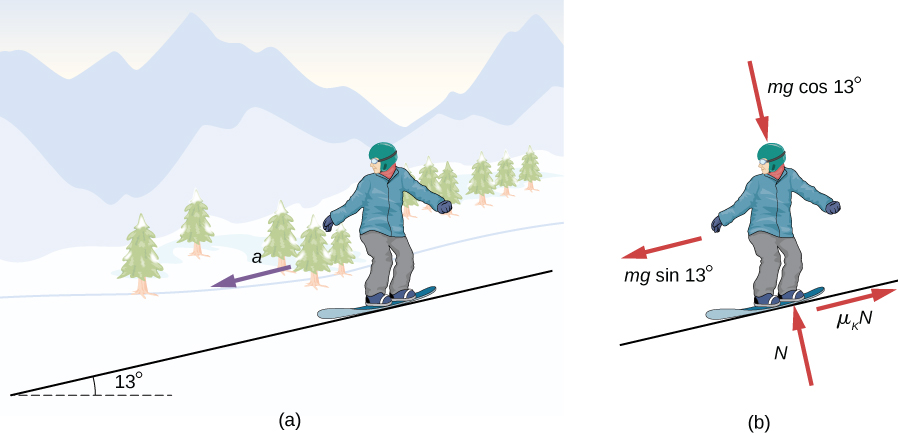
Estrategia
Las fuerzas que actúan sobre el esquiador son su peso y la fuerza de contacto de la pendiente, que tiene una componente normal a la inclinación y una componente a lo largo de la inclinación (fuerza de fricción cinética). Debido a que se mueve a lo largo de la pendiente, el marco de referencia más conveniente para analizar su movimiento es uno con el eje $x$ a lo largo del plano inclinado y el eje $y$ perpendicular a la inclinación.
En este marco, tanto las fuerzas normales como las de fricción se encuentran a lo largo de ejes coordenados, las componentes del peso son $mgsen\theta$ a lo largo de la pendiente y $mgcos\theta$ en ángulo recto con la pendiente, y la única aceleración es a lo largo del eje $x$ $(a_y = 0)$.
Solución
Ahora podemos aplicar la segunda ley de Newton al esquiador:
A partir de la segunda ecuación, $N = mgcos\theta$. Al sustituir esto en la primera ecuación, encontramos
$$a_x = g(sen\theta − \mu_kcos\theta) = g(sen13\degree - 0.20cos13\degree) = 0.29 m/s^2$$Explicación
Fíjate en esta ecuación que si $\theta$ es lo suficientemente pequeño o $\mu_k$ es lo suficientemente grande, $a_x$ es negativo, es decir, el esquiador se ralentiza.
 Comprueba tu aprendizaje 6.8
Comprueba tu aprendizaje 6.8
Fuerza centrípeta
En el capítulo de movimiento en dos y tres dimensiones, vimos los conceptos básicos del movimiento circular. Un objeto que se mueve circularmente, como uno de los autos de carreras que se muestran al inicio de este capítulo, debe estar acelerando porque está cambiando la dirección de su velocidad. Probamos que esta aceleración dirigida centralmente, llamada aceleración centrípeta, está dada por la fórmula
donde $v$ es la velocidad del objeto, dirigida a lo largo de una línea tangente a la curva en cualquier instante. Si conocemos la velocidad angular $\omega$, entonces podemos usar
$$a_c = r\omega^2$$La velocidad angular da la velocidad a la que el objeto está girando a través de la curva, en unidades de $rad/s$. Esta aceleración actúa a lo largo del radio de la trayectoria curva y, por lo tanto, también se denomina aceleración radial. Una aceleración debe ser producida por una fuerza. Cualquier fuerza o combinación de fuerzas puede causar una aceleración centrípeta o radial. Algunos ejemplos son la tensión en la cuerda que sujeta una bola, la fuerza de la gravedad terrestre en la Luna, la fricción entre patines y el suelo de la pista, la fuerza de un camino inclinado sobre un automóvil y fuerzas en el tubo de una centrífuga giratoria . Cualquier fuerza neta que causa un movimiento circular uniforme se llama fuerza centrípeta.
La dirección de una fuerza centrípeta es hacia el centro de curvatura, lo mismo que la dirección de la aceleración centrípeta. De acuerdo con la segunda ley del movimiento de Newton, la fuerza neta es la aceleración de la masa por tiempo: $F_{neta} = ma$. Para un movimiento circular uniforme, la aceleración es la aceleración centrípeta: $a = a_c$. Por lo tanto, la magnitud de la fuerza centrípeta $Fc es
$$F_c = ma_c$$Sustituyendo las expresiones de aceleración centrípeta
$\Big(a_c = \frac{v^2}{r}; \;\;a_c = r\omega^2\Big)$, obtenemos dos expresiones para la fuerza centrípeta $F_c$ en términos de masa, velocidad, velocidad angular y radio de curvatura:
Puedes usar cualquier expresión de fuerza centrípeta que sea más conveniente. La fuerza centrípeta $\bold{\vec{F}}_c$ es siempre perpendicular a la trayectoria y apunta al centro de curvatura, porque $\bold{\vec{a}}_c$ es perpendicular a la velocidad y apunta al centro de curvatura. Ten en cuenta que si resuelve la primera expresión para $r$, obtenemos
$$r = \frac{mv^2}{F_c}$$Esto implica que para una masa y velocidad dada, una gran fuerza centrípeta causa un pequeño radio de curvatura, es decir, una curva cerrada, como en la figura 6.20.
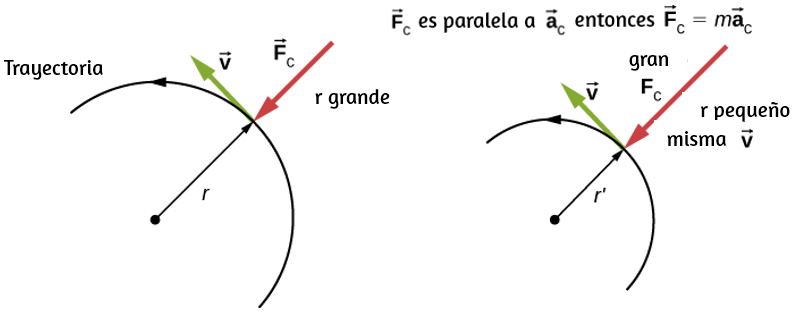
Ejemplo 6.15
¿Qué coeficiente de fricción necesitan los automóviles en una curva plana?
(a) Calcula la fuerza centrípeta ejercida sobre un automóvil de $900.0 kg$ que rueda sobre una curva de radio de $500.0 m$ a $25.00 m/s$. (b) Suponiendo una curva no peraltada, encuentra el coeficiente de fricción estático mínimo entre los neumáticos y la carretera, siendo la fricción estática la razón que impide que el automóvil se deslice (Figura 6.21).
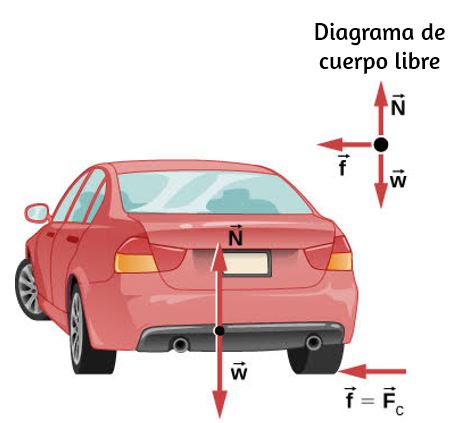
Estrategia
Sabemos que $F_c = m\frac{v^2}{r}$. Así,
$$F_c = \frac{(900.0 kg)(25.00 m/s)^2}{r} = \frac{mv^2}{(500.0 m)} = 1125 N$$La Figura 6.21 muestra las fuerzas que actúan sobre el automóvil en una curva no bancarizada (nivel plano). La fricción está a la izquierda, lo que impide que el automóvil se deslice, y debido a que es la única fuerza horizontal que actúa sobre el automóvil, la fricción es la fuerza centrípeta en este caso. Sabemos que la fricción estática máxima (a la cual los neumáticos ruedan, pero no resbalan) es $\mu_sN$, donde $\mu_s$ es el coeficiente de fricción estático y $N$ es la fuerza normal. La fuerza normal es igual al peso del auto en terreno llano, entonces $N = mg$. Por lo tanto, la fuerza centrípeta en esta situación es
$$F_c \equiv f = \mu_sN = \mu_smg$$Ahora tenemos una relación entre la fuerza centrípeta y el coeficiente de fricción. Usando la ecuación
$$F_c = m\frac{v^2}{r} \implies m\frac{v^2}{r} = \mu_smg$$Resolvemos esto para $\mu_s$, observando que la masa se cancela, y obtenemos
$$\mu_s = \frac{v^2}{rg}$$Sustituyendo:
(Debido a que los coeficientes de fricción son aproximados, la respuesta se da a solo dos dígitos).
Explicación
El coeficiente de fricción que se encuentra en la Figura 6.21 (b) es mucho más pequeño que el que se encuentra típicamente entre los neumáticos y las carreteras. El automóvil todavía rueda en la curva si el coeficiente es mayor que $0.13$, porque la fricción estática es una fuerza sensible, capaz de asumir un valor menor que, pero no más que $\mu_sN$. Un coeficiente más alto también permitiría que el automóvil ruede sobre la curva a una velocidad más alta, pero si el coeficiente de fricción es menor, la velocidad de seguridad sería inferior a $25 m/s$. Ten en cuenta que la masa se cancela, lo que implica que, en este ejemplo, no importa qué tan cargado esté el automóvil para realizar el giro. La masa se cancela porque la fricción se supone proporcional a la fuerza normal, que a su vez es proporcional a la masa. Si la superficie de la carretera se acumulara, la fuerza normal sería menor, como veremos a continuación.
 Comprueba tu aprendizaje 6.9
Comprueba tu aprendizaje 6.9
Curvas con peraltes
Consideremos ahora las curvas peraltadas, donde la pendiente del camino ayuda a rodar la curva (Figura 6.22). Cuanto mayor es el ángulo $\theta$, más rápido puedes tomar la curva. Las pistas de carreras para bicicletas y automóviles, por ejemplo, a menudo tienen curvas muy inclinadas. En una "curva peraltada idealmente", el ángulo $\theta$ es tal que puedes rodar por la curva a una cierta velocidad sin la ayuda de la fricción entre los neumáticos y la carretera. Obtendremos una expresión para $\theta$ en una curva idealmente peraltada y consideraremos un ejemplo relacionado con ella.
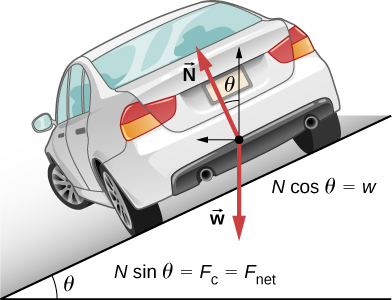
Para una banca ideal, la fuerza externa neta es igual a la fuerza centrípeta horizontal en ausencia de fricción. Los componentes de la fuerza normal N en las direcciones horizontal y vertical deben ser iguales a la fuerza centrípeta y al peso del automóvil, respectivamente. En los casos en que las fuerzas no son paralelas, es más conveniente considerar componentes a lo largo de ejes perpendiculares, en este caso, las direcciones vertical y horizontal.
La Figura 6.22 muestra un diagrama de cuerpo libre para un automóvil en una curva con banca sin fricción. Si el ángulo $\theta$ es ideal para la velocidad y el radio, entonces la fuerza externa neta es igual a la fuerza centrípeta necesaria. Las únicas dos fuerzas externas que actúan sobre el automóvil son su peso $\bold{\vec{w}}$ y la fuerza normal de la carretera $\bold{\vec{N}}$ (una superficie sin fricción solo puede ejercer una fuerza perpendicular a la superficie, es decir, una fuerza normal). Estas dos fuerzas deben sumarse para dar una fuerza externa neta que es horizontal hacia el centro de curvatura y tiene una magnitud $mv^2/r$. Debido a que esta es la fuerza crítica y es horizontal, utilizamos un sistema de coordenadas con ejes verticales y horizontales. Solo la fuerza normal tiene un componente horizontal, por lo que debe ser igual a la fuerza centrípeta, es decir,
$$Nsen\theta = \frac{mv^2}{r}$$Debido a que el automóvil no abandona la superficie de la carretera, la fuerza vertical neta debe ser cero, lo que significa que las componentes verticales de las dos fuerzas externas deben ser iguales en magnitud y opuestas en la dirección. En la Figura 6.22, vemos que la componente vertical de la fuerza normal es $Ncos\theta$, y la única otra fuerza vertical es el peso del automóvil. Estos deben ser iguales en magnitud; así,
$$N cos\theta = mg$$Ahora podemos combinar estas dos ecuaciones para eliminar $N$ y obtener una expresión para $\theta$, como se deseaba. Resolviendo la segunda ecuación para $N = mg/(cos\theta)$ y sustituyéndola en la ecuación anterior:
Calulando la inversa de la tangente, obtenemos
Esta expresión puede entenderse considerando cómo $\theta$ depende de $v$ y $r$. Se obtiene un ángulo $\theta$ grande para una $v$ grande y una $r$ pequeña. Es decir, las carreteras deben tener una inclinación abrupta para altas velocidades y curvas pronunciadas. La fricción ayuda, porque le permite tomar la curva a mayor o menor velocidad que si la curva no tuviera fricción. Ten en cuenta que $\theta$ no depende de la masa del vehículo.
Ejemplo 6.16
¿Cuál es la velocidad ideal para tomar una curva cerrada firmemente inclinada?
Las curvas en algunas pistas de prueba y carreras, como el Daytona International Speedway en Florida, están muy peraltadas. Esta banca, con la ayuda de la fricción de los neumáticos y las configuraciones de automóviles muy estables, permite que las curvas se tomen a una velocidad muy alta.
Para ilustrar, calcula la velocidad a la que una curva de $100.0 m$ de radio peraltada a $31.0\degree$ debe conducirse si la carretera no tiene fricción.
Estrategia
Primero notamos que todos los términos en la expresión para el ángulo ideal de una curva peraltada a excepción de la velocidad son conocidos; por lo tanto, solo tenemos que reorganizarlo para que la velocidad aparezca en el lado izquierdo y luego sustituir cantidades conocidas.
Solución
Empezando con
$$tan\theta = \frac{v^2}{rg}$$Obtenemos
$$v = \sqrt{rgtan\theta}$$Teniendo en cuenta que $tan 31.0\degree = 0.609$, obtenemos
$$v = \sqrt{(100.0 m)(9.80 m/s^2)(0.609)} = 24.4 m/s$$Explicación
Esto es solo alrededor de $165 km/h$, consistente con una curva muy inclinada y bastante pronunciada.
La fricción de los neumáticos permite que un vehículo tome la curva a velocidades significativamente más altas.
Los aviones también se turnan con los peraltes. La fuerza de elevación, debido a la fuerza del aire en el ala, actúa en ángulo recto con el ala. Cuando el avión se peraltea, el piloto está obteniendo una sustentación mayor de la necesaria para un vuelo nivelado. El componente vertical del ascenso equilibra el peso del avión y la componente horizontal acelera el avión. El ángulo del peralte que se muestra en la Figura 6.23 viene dado por $\theta$. Analizamos las fuerzas de la misma manera en que tratamos el caso del automóvil que rodea una curva apilada.
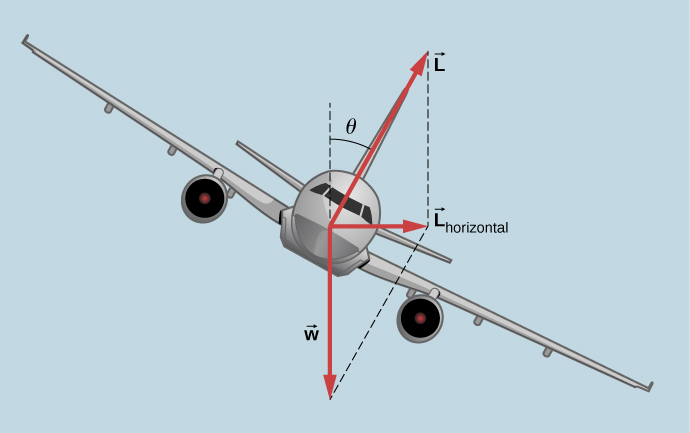
Modelo de Tiovivo (Fuerza Centrípeta)
La velocidad de un cuerpo, en módulo, dirección y sentido, permanece constante de acuerdo con la primera ley de Newton (ley de la inercia) si no actúa ninguna fuerza sobre el o la resultante de todas las fuerzas que actúan es cero. Las circunstancias de un movimiento circular son diferentes: En este caso debe haber una fuerza, llamada fuerza centrípeta, dirigida hacia el eje de rotación. Este modelo sencillo de un tiovivo muestra esta fuerza.
Si selecciona la segunda de las cuatro opciones que se encuentran en la parte superior derecha del modelo interactivo, se dibujarán los vectores de las fuerzas que se ejercen sobre cada una de las ocho masas de los péndulos: la fuerza del peso se dibuja en negro, la fuerza ejercida por la cuerda de azul. La suma de estos vectores nos da la fuerza resultante (roja) que es la fuerza centrípeta que apunta hacia adentro y que se mencionó antes.
Además de la simulación del tiovivo (con las flechas que representan las fuerzas o sin ellas) el programa ofrece un boceto bidimensional de los vectores fuerzas y valores importantes del movimiento circular.
Si deseas observar con detenimiento las flechas de las fuerzas, puedes detener el giro utilizando el botón "Pausa / Reanudar" o hacerlo diez veces más lento con la opción "Movimiento lento". Los campos de texto permiten variar los parámetros entre ciertos límites (¡no olvides presionar la tecla "Intro"!).
Nota: La simulación supone un movimiento circular con velocidad angular constante; los procesos mientras las masas se aceleran o enlentecen no se tienen en cuenta. También se desprecian los efectos de la resistencia del aire.
El modelo interactivo fue tomado del repositorio de Walter Fendt
Fuerzas inerciales y marcos no originales (acelerados): la fuerza de Coriolis
¿Qué tienen en común el despegue en un avión a reacción, doblar una esquina en un automóvil, montar en un carrusel y el movimiento circular de un ciclón tropical? Cada uno exhibe fuerzas inerciales, fuerzas que simplemente parecen surgir del movimiento, porque el marco de referencia del observador se está acelerando o rotando. Al despegar en un avión, la mayoría de la gente estaría de acuerdo en que se siente como si lo estuvieran empujando hacia atrás en el asiento mientras el avión acelera en la pista. Sin embargo, un físico diría que tiendes a permanecer inmóvil mientras el asiento te empuja. Una experiencia aún más común ocurre cuando haces una curva cerrada en tu automóvil, por ejemplo, hacia la derecha (Figura 6.24).
Te sientes como si hubieras sido arrojado (es decir, forzado) hacia la izquierda en relación con el automóvil. Una vez más, un físico diría que vas en línea recta (recuerda la primera ley de Newton) pero el automóvil se mueve hacia la derecha, no es que estés experimentando una fuerza desde la izquierda.
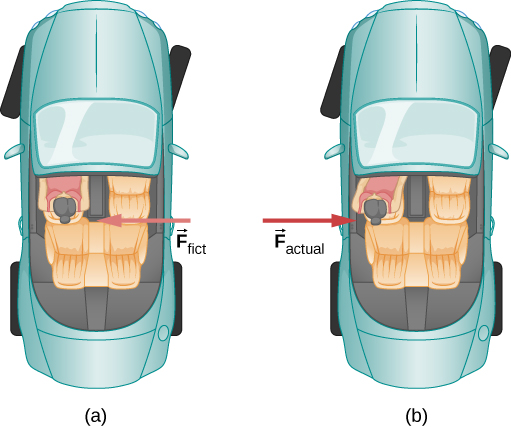
Podemos reconciliar estos puntos de vista examinando los marcos de referencia utilizados. Concentrémonos en las personas en un automóvil. Los pasajeros usan instintivamente el automóvil como marco de referencia, mientras que un físico puede usar la Tierra.
El físico podría hacer esta elección porque la Tierra es casi un marco de referencia inercial, en el que todas las fuerzas tienen un origen físico identificable. En tal marco de referencia, las leyes del movimiento de Newton toman la forma dada. El automóvil es un marco de referencia no original porque se acelera hacia un lado. La fuerza hacia la izquierda detectada por los pasajeros del automóvil es una fuerza inercial que no tiene un origen físico (se debe puramente a la inercia del pasajero, no a una causa física como la tensión, la fricción o la gravitación). El auto, al igual que el conductor, en realidad está acelerando hacia la derecha. Se dice que esta es una fuerza inercial porque no tiene un origen físico, como la gravedad.
Un físico elegirá el marco de referencia más conveniente para la situación que se analiza. No hay problema para un físico en incluir fuerzas de inercia y la segunda ley de Newton, como de costumbre, si es más conveniente, por ejemplo, en un tiovivo o en un planeta en rotación. Se utilizan marcos de referencia no originales (acelerados) cuando es útil hacerlo. Se deben considerar diferentes marcos de referencia al analizar el movimiento de un astronauta en una nave espacial que viaja a velocidades cercanas a la velocidad de la luz, como apreciaráS en el estudio de la teoría especial de la relatividad.
Démonos un paseo mental en un tiovivo, específicamente, un carrusel de patio de recreo que gira rápidamente (Figura 6.25). Tomas el tiovivo como tu marco de referencia porque rotan juntos. Al girar en ese marco de referencia no original, sientes una fuerza inercial que tiende a tirarte; esto a menudo se conoce como una fuerza centrífuga (que no debe confundirse con la fuerza centrípeta). La fuerza centrífuga es un término comúnmente usado, pero en realidad no existe. Debes aguantar bien para contrarrestar tu inercia (a la que las personas suelen llamar fuerza centrífuga). En el marco de referencia de la Tierra, no hay fuerza que intente desanimarte; enfatizamos que la fuerza centrífuga es una ficción.
Debes esperar para darte vuelta en círculo porque, de lo contrario, irías en línea recta, justo fuera del carrusel, de acuerdo con la primera ley de Newton. Pero la fuerza que ejerces actúa hacia el centro del círculo.
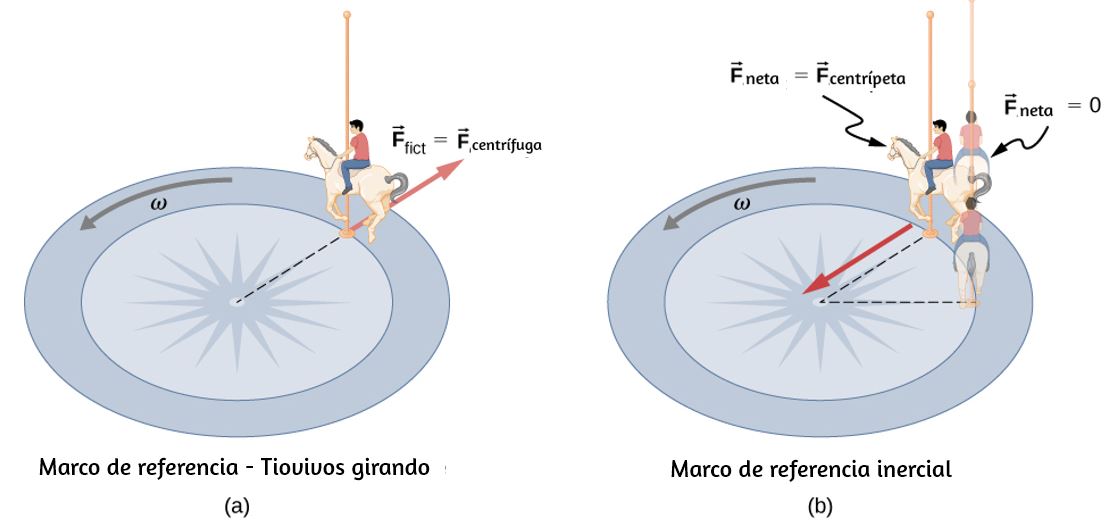
Este efecto de inercia, que te aleja del centro de rotación, si no hay fuerza centrípeta para causar un movimiento circular, se aprovecha en centrifugadoras (Figura 6.26). Una centrífuga hace girar una muestra muy rápidamente. Visto desde el marco de referencia giratorio, la fuerza inercial arroja las partículas hacia afuera, acelerando su sedimentación. Cuanto mayor es la velocidad angular, mayor es la fuerza centrífuga. Pero lo que realmente sucede es que la inercia de las partículas las lleva a lo largo de una línea tangente al círculo, mientras que el tubo de ensayo se ve forzado en una trayectoria circular por una fuerza centrípeta.
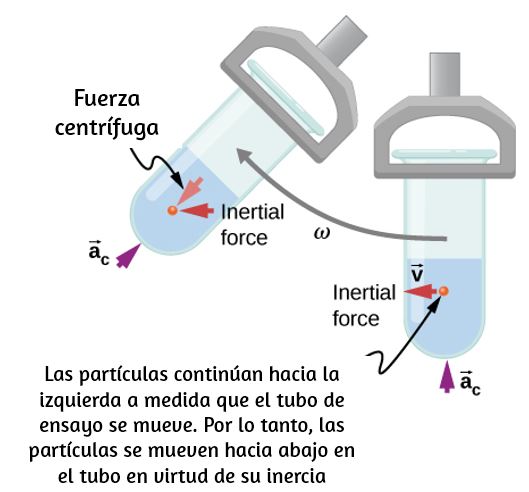
Consideremos ahora qué pasa si algo se mueve en un marco de referencia rotativo. Por ejemplo, ¿qué pasa si deslizas una pelota directamente lejos del centro del tiovivo, como se muestra en la Figura 6.27? La bola sigue un camino recto con respecto a la Tierra (asumiendo una fricción insignificante) y un camino curvado hacia la derecha en la superficie del carrusel. Una persona de pie junto al tiovivo ve la pelota moviéndose en línea recta y el tiovivo girando debajo de ella. En el marco de referencia del tiovivo, explicamos la curva aparente hacia la derecha utilizando una fuerza inercial, llamada fuerza de Coriolis, que hace que la bola se curve hacia la derecha.
La fuerza de Coriolis puede ser utilizada por cualquiera en ese marco de referencia para explicar por qué los objetos siguen trayectorias curvas y nos permite aplicar las leyes de Newton en marcos de referencia no originales.
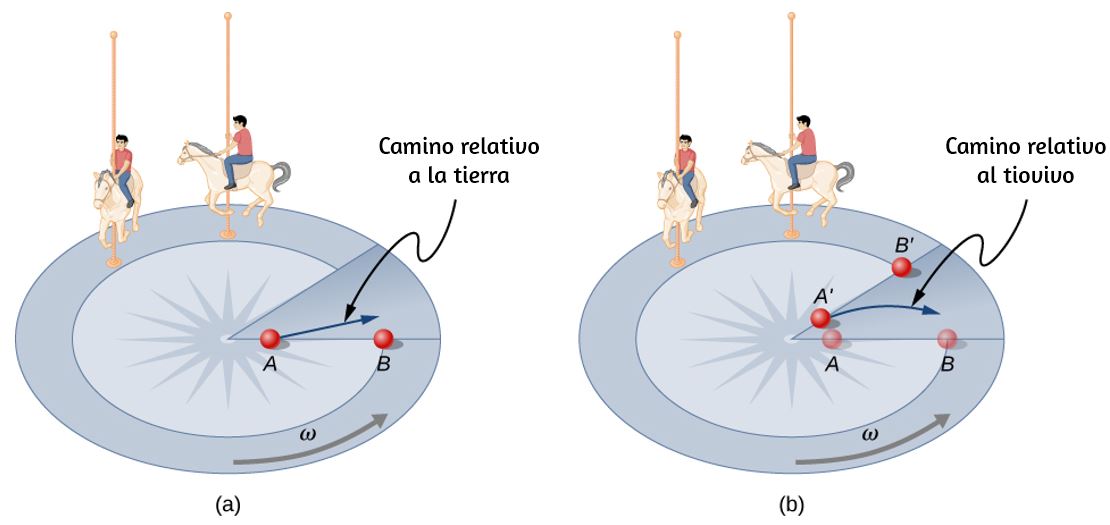
Hasta ahora, hemos considerado que la Tierra es un marco de referencia inercial con poca o ninguna preocupación acerca de los efectos debido a su rotación. Sin embargo, tales efectos existen, por ejemplo, en la rotación de los sistemas climáticos. La mayoría de las consecuencias de la rotación de la Tierra pueden ser entendidas cualitativamente por analogía con el tiovivo. Vista desde arriba del Polo Norte, la Tierra gira en sentido antihorario, como lo hace el tiovivo en la Figura 6.27. Como en el tiovivo, cualquier movimiento en el hemisferio norte de la Tierra experimenta una fuerza de Coriolis a la derecha. Todo lo contrario ocurre en el Hemisferio Sur; allí, la fuerza está a la izquierda.
Debido a que la velocidad angular de la Tierra es pequeña, la fuerza de Coriolis suele ser insignificante, pero para los movimientos a gran escala, como los patrones del viento, tiene efectos sustanciales.
La fuerza de Coriolis causa que los huracanes en el hemisferio norte giren en el sentido contrario a las agujas del reloj, mientras que los ciclones tropicales en el hemisferio sur rotan en el sentido de las agujas del reloj. (Los términos huracán, tifón y tormenta tropical son nombres regionales específicos para ciclones, que son sistemas de tormentas caracterizados por centros de baja presión, fuertes vientos y fuertes lluvias). La Figura 6.28 ayuda a mostrar cómo se producen estas rotaciones. El aire fluye hacia cualquier región de baja presión, y los ciclones tropicales contienen presiones particularmente bajas. Por lo tanto, los vientos fluyen hacia el centro de un ciclón tropical o un sistema meteorológico de baja presión en la superficie. En el hemisferio norte, estos vientos hacia adentro se desvían hacia la derecha, como se muestra en la figura, produciendo una circulación en sentido antihorario en la superficie para zonas de baja presión de cualquier tipo. La baja presión en la superficie se asocia con el aumento de aire, que también produce enfriamiento y formación de nubes, haciendo que los patrones de baja presión sean bastante visibles desde el espacio. Por el contrario, la circulación del viento alrededor de las zonas de alta presión es en el sentido de las agujas del reloj en el Hemisferio Sur, pero es menos visible porque la alta presión está asociada con el aire que se hunde, produciendo cielos despejados.
La rotación de los ciclones tropicales y la trayectoria de una pelota en un carrusel también pueden explicarse por la inercia y la rotación del sistema que se encuentra debajo. Cuando se utilizan marcos no originales, se deben inventar fuerzas de inercia, como la fuerza de Coriolis, para explicar la trayectoria curva. No hay una fuente física identificable para estas fuerzas de inercia.
En un marco inercial, la inercia explica el camino, y no se encuentra ninguna fuerza sin una fuente identificable. Cualquier punto de vista nos permite describir la naturaleza, pero uno de ellos es un marco inercial, pues todas las fuerzas tienen orígenes y explicaciones.
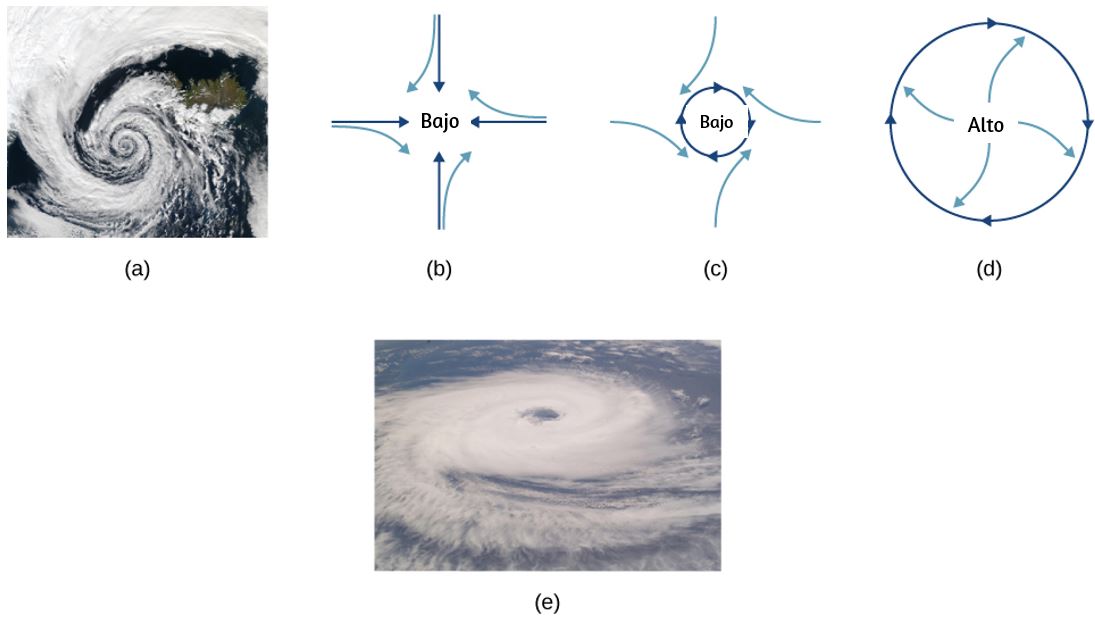
Fuerza de arrastre y velocidad terminal
Otra fuerza interesante en la vida cotidiana es la fuerza de arrastre sobre un objeto cuando se mueve en un fluido (ya sea un gas o un líquido). Sientes la fuerza de arrastre cuando mueves tu mano a través del agua. También puedes sentirla si mueves tu mano durante un viento fuerte. Cuanto más rápido muevas tu mano, más difícil será moverla. Siente una fuerza de arrastre menor cuando inclinas la mano para que solo el lado pase por el aire; ha disminuido el área de la mano que mira en la dirección del movimiento.
Fuerzas de arrastre
Al igual que la fricción, la fuerza de arrastre siempre se opone al movimiento de un objeto. A diferencia de la fricción simple, la fuerza de arrastre es proporcional a alguna función de la velocidad del objeto en ese fluido. Esta funcionalidad es complicada y depende de la forma del objeto, su tamaño, su velocidad y el fluido en el que se encuentra. Para la mayoría de objetos grandes como ciclistas, autos y pelotas de béisbol que no se mueven demasiado despacio, la magnitud de la fuerza de arrastre $F_D$ es proporcional al cuadrado de la velocidad del objeto. Podemos escribir esta relación matemáticamente como $F_D\prop v^2$. Al tomar en cuenta otros factores, esta relación se vuelve
donde $C$ es el coeficiente de arrastre, $A$ es el área del objeto que está frente al fluido, y $\rho$ es la densidad del fluido (Recuerda que la densidad es masa por unidad de volumen).
Esta ecuación también se puede escribir de forma más general como $F_D = bv^2$, donde $b$ es una constante equivalente a $0.5C_{\rho}A$. Hemos establecido el exponente $n$ para estas ecuaciones como $2$ porque cuando un objeto se mueve a alta velocidad a través del aire, la magnitud de la fuerza de arrastre es proporcional al cuadrado de la velocidad. Como veremos en Mecánica de Fluidos, para partículas pequeñas que se mueven a bajas velocidades en un fluido, el exponente $n$ es igual a $1$.
La fuerza de arrastre $F_D$ es proporcional al cuadrado de la velocidad del objeto. Matemáticamente, $$F_D = \frac12 C_{\rho}Av^2$$ donde $C$ es el coeficiente de arrastre, $A$ es el área del objeto que está frente al fluido, y $\rho$ρ es la densidad del fluido.
Tanto los atletas como los diseñadores de automóviles buscan reducir la fuerza de arrastre para disminuir sus tiempos de carrera (Figura 6.29). La forma aerodinámica de un automóvil puede reducir la fuerza de arrastre y así aumentar el consumo de combustible de un automóvil.
El valor del coeficiente de arrastre $C$ se determina empíricamente, generalmente con el uso de un túnel de viento (Figura 6.30).


El coeficiente de arrastre puede depender de la velocidad, pero suponemos que es una constante aquí. La Tabla 6.2 enumera algunos coeficientes de arrastre típicos para una variedad de objetos. Ten en cuenta que el coeficiente de arrastre es una cantidad adimensional. A velocidades de autopista, más del $50%$ de la potencia de un automóvil se usa para superar la resistencia al aire. La velocidad de crucero más eficiente en consumo de combustible es de aproximadamente $70-80 km/h$ (alrededor de $45-50 mi/h$). Por esta razón, durante la crisis del petróleo de los años setenta en los Estados Unidos, las velocidades máximas en las carreteras se establecieron a aproximadamente $90 km/h$ ($55 mi/h$).
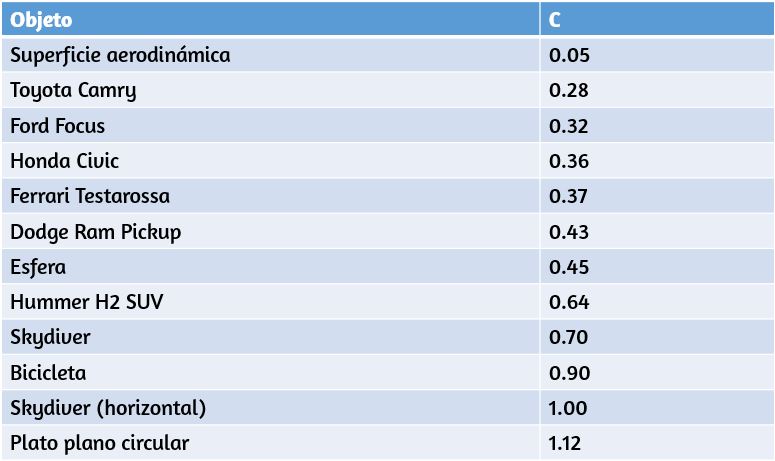
Se están llevando a cabo importantes investigaciones en el mundo deportivo para minimizar el arrastre. Los hoyuelos en las pelotas de golf están siendo rediseñados, al igual que la ropa que usan los atletas.
Los corredores de bicicletas y algunos nadadores y corredores usan monos llenos. La australiana Cathy Freeman vistió un traje de cuerpo completo en los Juegos Olímpicos de Sydney 2000 y ganó una medalla de oro en la carrera de $400 m$. Muchos nadadores en los Juegos Olímpicos de Beijing 2008 llevaban trajes de cuerpo (Speedo); podría haber hecho una diferencia al romper muchos récords mundiales (Figura 6.31). La mayoría de los nadadores de élite (y ciclistas) se afeitan el pelo. Tales innovaciones pueden tener el efecto de cortar milisegundos en una carrera, a veces haciendo la diferencia entre una medalla de oro y una de plata. Una consecuencia es que las pautas cuidadosas y precisas se deben desarrollar continuamente para mantener la integridad del deporte.

Velocidad terminal
Algunas situaciones interesantes relacionadas con la segunda ley de Newton ocurren cuando se consideran los efectos de las fuerzas de arrastre sobre un objeto en movimiento. Por ejemplo, considera un paracaidista que cae al aire bajo la influencia de la gravedad. Las dos fuerzas que actúan sobre él son la fuerza de la gravedad y la fuerza de arrastre (ignorando la pequeña fuerza de flotación). La fuerza hacia abajo de la gravedad permanece constante independientemente de la velocidad a la que la persona se está moviendo. Sin embargo, a medida que la velocidad de la persona aumenta, la magnitud de la fuerza de arrastre aumenta hasta que la magnitud de la fuerza de arrastre sea igual a la fuerza de la gravedad, produciendo así una fuerza neta de cero. Una fuerza neta cero significa que no hay aceleración, como lo muestra la segunda ley de Newton. En este punto, la velocidad de la persona permanece constante y decimos que la persona ha alcanzado su velocidad terminal ($v_T$). Como $F_D$ es proporcional a la velocidad al cuadrado, un paracaidista más pesado debe ir más rápido para que $F_D$ iguale su peso. Veamos cómo funciona esto de manera más cuantitativa.
En la velocidad terminal,
$$F_{neta} = mg − F_D = ma =0$$Despejando,
$$mg = F_D$$Usando la ecuación para la fuerza de arrastre, tenemos
$$mg = \frac12C_{\rho}Av_T^2$$Despejando la velocidad, obtenemos
$$v_T = \sqrt{\frac{2mg}{\rho CA}}$$Supón que la densidad del aire es $\rho = 1.21 kg/m^3$. El paracaidista de $75$ kg que desciende primero tiene un área de sección transversal de aproximadamente $A = 0.18m^2$ y un coeficiente de arrastre de aproximadamente $C = 0.70$. Encontramos que,
$$v_T = \sqrt{\frac{2(75kg)(9.80m/s^2)} {(1.21 kg/m^3)(0.70)(0.18m^2)}} = 9.8 m/s = 350 km/h$$Esto significa que un paracaidista con una masa de $75 kg$ logra una velocidad máxima de aproximadamente $350 km/h$ mientras viaja en una posición de picada (cabeza primero), minimizando el área y su resistencia. En una posición de águila extendida, esa velocidad terminal puede disminuir a aproximadamente a $200 km/h$ a medida que aumenta el área. Esta velocidad terminal se vuelve mucho más pequeña después de que se abre el paracaídas.
Ejemplo 6.17
Velocidad terminal de un paracaidista
Encuentra la velocidad terminal de un paracaidista de $85 kg$ que cae en posición de águila extendida.
Estrategia
En velocidad terminal, $F_{neta} = 0$.
Por lo tanto, la fuerza de arrastre en el paracaidista debe ser igual a la fuerza de la gravedad (el peso de la persona).
Usando la ecuación de fuerza de arrastre, encontramos $mg = \frac12C_{\rho}Av^2$
Solución
La velocidad terminal $v_T$ se puede escribir como
$$v_T = \sqrt{{2mg}{\rho CA}} = \sqrt{\frac{2(85kg)(9.80 m/s^2)}{(1.21 kg/m^3)(1.0)(0.70m^2)}} = 44m/s$$Explicación
Este resultado es consistente con el valor de $v_T$ mencionado anteriormente. El paracaidista de $75 kg$ que iba primero en picada tenía una velocidad terminal de $v_T = 98 m/s$. Pesaba menos, pero tenía un área frontal más pequeña y, por lo tanto, una menor resistencia al aire.
 Comprueba tu aprendizaje 6.10
Comprueba tu aprendizaje 6.10
El tamaño del objeto que cae por el aire presenta otra aplicación interesante de resistencia aerodinámica. Si se cae de una rama de un árbol de $5 m$ de altura, es probable que se lastime, posiblemente fracturando un hueso.
Sin embargo, una pequeña ardilla hace esto todo el tiempo, sin lastimarse. No alcanzas una velocidad terminal en una distancia tan corta, pero la ardilla sí.
La siguiente cita interesante sobre el tamaño de los animales y la velocidad terminal proviene de un ensayo de 1928 realizado por un biólogo británico, J. B. S. Haldane, titulado "Sobre el tamaño correcto".
Para el ratón y cualquier animal más pequeño, ésta [la gravedad] prácticamente no representa ningún peligro. Podemos arrojar a un ratón a un pozo de mil metros y al llegar al fondo, sufre una pequeña conmoción pero se aleja caminando. Una rata probablemente se mataría, aunque puede caer sin peligro desde un undécimo piso; un hombre se mataría, un caballo salpicaría. Y esto es porque la resistencia al movimiento que presenta el aire es proporcional a la superficie del objeto en movimiento. Dividamos entre diez el largo, ancho y alto de un animal; su peso se reduce a un milésimo, pero su superficie a un centésimo. Por lo tanto, la resistencia a caer en el caso del pequeño animal es relativamente diez veces mayor".
La dependencia cuadrática anterior de la resistencia aerodinámica a la velocidad no se cumple si el objeto es muy pequeño, va muy lento o está en un medio más denso que el aire. Luego, encontramos que la fuerza de arrastre es proporcional solo a la velocidad. Esta relación está dada por la ley de Stokes.
Para un objeto esférico que cae en un medio, la fuerza de arrastre es $$F_s = 6\pi r\eta v\tag{6.6}$$
Buenos ejemplos de la ley de Stokes son proporcionados por microorganismos, polen y partículas de polvo. Debido a que cada uno de estos objetos son tan pequeños, encontramos que muchos viajan sin ayuda solo a una velocidad constante (terminal). Las velocidades terminales para bacterias (tamaño alrededor de $1\mu m$) pueden ser de aproximadamente $2 \mu m/s$. Para moverse a mayor velocidad, muchas bacterias nadan usando flagelos (organelos con forma de pequeñas colas) que funcionan como pequeños motores incrustados en la célula.
Los sedimentos en un lago pueden moverse a una mayor velocidad terminal (alrededor de $5 \mu m/s$), por lo que pueden pasar varios días hasta que lleguen al fondo del lago después de haber sido depositados en la superficie.
Si comparamos los animales que viven en la tierra con los que están en el agua, puedes ver cómo la resistencia ha influido en la evolución. Los peces, los delfines y hasta las ballenas tienen una forma aerodinámica para reducir las fuerzas de arrastre. Las aves se racionalizan y las especies migratorias que vuelan grandes distancias a menudo tienen características particulares, como cuellos largos. Las bandadas de pájaros vuelan en forma de punta de lanza a medida que la bandada forma un patrón aerodinámico (Figura 6.32).
En los seres humanos, un ejemplo importante de racionalización es la forma de los espermatozoides, que deben ser eficientes en el uso de la energía.

El cálculo de las fuerzas friccionales dependientes de la velocidad
Cuando un cuerpo se desliza sobre una superficie, la fuerza de fricción es aproximadamente constante y está dada por $\mu_kN$. Desafortunadamente, la fuerza de fricción en un cuerpo que se mueve a través de un líquido o un gas no se comporta de manera tan simple.
Esta fuerza de arrastre generalmente es una función complicada de la velocidad del cuerpo. Sin embargo, para un cuerpo que se mueve en línea recta a velocidades moderadas a través de un líquido como el agua, la fuerza de fricción a menudo se puede aproximar mediante
$$f_R = -bv$$donde $b$ es una constante cuyo valor depende de las dimensiones y la forma del cuerpo y las propiedades del líquido, y $v$ es la velocidad del cuerpo. Dos situaciones para las cuales la fuerza de fricción se puede representar con esta ecuación son una lancha a motor que se mueve a través del agua y un pequeño objeto que cae lentamente a través de un líquido.
Consideremos un objeto caer a través de un líquido. El diagrama de cuerpo libre de este objeto con la dirección positiva hacia abajo se muestra en la Figura 6.33. La segunda ley de Newton en la dirección vertical da la ecuación diferencial
$$mg − bv = m\frac{dv}{dt}$$donde hemos escrito la aceleración como $dv/dt$. A medida que $v$ aumenta, la fuerza de fricción $-bv$ aumenta hasta que coincide con $mg$. En este punto, no hay aceleración y la velocidad permanece constante a la velocidad terminal $v_T$. De la ecuación anterior,
$$mg - bv_T = 0$$ $$v_T = \frac{mg}{b}$$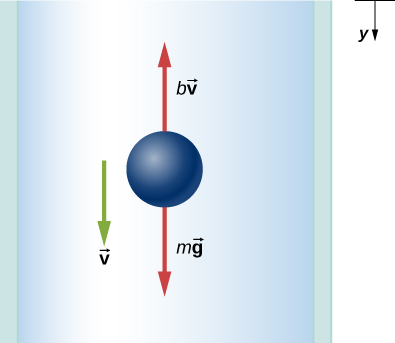
Podemos encontrar la velocidad del objeto integrando la ecuación diferencial para $v.$ Primero, reorganizamos los términos en esta ecuación para obtener
$$\frac{dv}{g − (b/m)v} = dt$$Suponiendo que $v = 0$ en $t = 0$, la integración de esta ecuación sería:
$$\int_0^v \frac{dv'}{g − (b/m)v'} = \int_0^v \frac{t}{dt'}$$Resolviendo la integral
$$-\frac{m}{b}ln\Big(g -\frac{b}{m}v'\Big)\Big]_0^t = t'\Big]_0^t$$donde $v'$ y $t'$ son variables ficticias de integración. Con los límites dados, encontramos
$$-\frac{m}{b}\Big[ln\Big(g - \frac{b}{m}v'\Big) - ln g\Big] = t$$Como $lnA - lnB = ln(A/B$), y $ln(A/B) = x $implica que $e^x = A/B$, entonces:
$$\frac{g − (bv/m)}{g} = e^{-bt/m}$$Luego,
$$v = \frac{mg}{b}\Big(1 - e^{-bt/m}\Big)$$Observa que como $t \to \infin, v \to mg/b = v_T$, que es la velocidad terminal.
La posición en cualquier momento se puede encontrar integrando la ecuación para $v$. Con $v = dy/dt$,
$$dy = \frac{mg}{b}\Big(1 - e^{-bt/m}\Big)dt$$Suponiendo que $y = 0$ cuando $t = 0$,
$$\int_0^y dy' = \frac{mg}{b}\int_0^t \Big(1 - e^{-bt'/m}\Big)dt'$$Al integrar, obtenemos:
$$y = \frac{mg}{b}t + \frac{m^2g}{b^2}\big(e^{-bt/m} - 1\big)$$Ejemplo 6.18
Efecto de la fuerza resistiva en una lancha
Una lancha a motor se mueve a través de un lago a una velocidad $v_0$ cuando su motor se congela repentinamente y se detiene. El barco entonces disminuye la velocidad bajo la fuerza de fricción $f_R = -bv$. (a) ¿Cuál es la velocidad y la posición del barco como funciones del tiempo? (b) Si el barco disminuye la velocidad de $4.0$ a $1.0 m/s$ en $10 s$, ¿qué distancia recorre antes de detenerse?
Solución
a. Con el motor parado, la única fuerza horizontal en el bote es $f_R = -bv$, por lo que según la segunda ley de Newton,
$$m\frac{dv}{dt} = -bv$$la expresión anterior la podemos escribir como:
$$\frac{dv}{v} = -\frac{b}{m}dt$$integrando esta ecuación entre el tiempo cero cuando la velocidad es $v_0$ y el tiempo $t$ cuando la velocidad es $v$, tenemos
$$\int_0^v \frac{dv'}{v'} = -\frac{b}{m}\int_0^t dt'$$Al resolver las integrales, obtenemos:
$$ln\frac{v}{v_0} = -\frac{b}{m}t$$Como $lnA = x$, entonces $e^x = A$. Podemos escribir esto como
$$v = v_0e^{-bt/m}$$Ahora, desde la definición de velocidad
$$\frac{dx}{dt} = v_0e^{-bt/m}$$entonces tenemos
$$dx = v_0e^{-bt/m}dt$$Con la posición inicial cero, tenemos
$$\int_0^x dx' = v_0\int_0^t e^{-bt'/m}dt'$$y
$$x = -\frac{mv_0}{b}e^{-bt'/m}\Big]_0^t = \frac{mv_0}{b}\big(1 - e^{-bt/m}\big)$$A medida que aumenta el tiempo, $e^{-bt/m} \to 0$, y la posición de la lancha se aproxima a un valor límite
$$x_{max} = \frac{mv_0}{b}$$Aunque esto nos dice que el barco tarda una cantidad de tiempo infinita para alcanzar $x_{max}$, la lancha se detiene efectivamente después de un tiempo razonable. Por ejemplo, en $t = 10 m/b$, tenemos
$$v = v_0e^{−10} \approx 4.5\times 10^{−5}v_0$$considerando que también tenemos
$$x = x_{max}\big(1 - e^{−10}\big) \approx 0.99995x_{max}$$Por lo tanto, la velocidad y posición del bote han alcanzado esencialmente sus valores finales.
b. Con $v_0 = 4.0 m/s$ y $v = 1.0 m/s$, tenemos $1.0m / s = (4.0 m/s) e^{-(b/m)(10s)}$, entonces
$$ln 0.25 = −ln 4.0 = −\frac{b}{m}(10s)$$y
$$\frac{b}{m} = \frac{1}{10}ln 4.0 s^{-1} = 0.14 s^{-1}$$Ahora, la posición límite de la lancha es
$$x_{max} = \frac{mv_0}{b} = \frac{4.0 m/s}{0.14 s^{-1}} = 29m$$Explicación
En los dos ejemplos anteriores, encontramos valores "limitantes". La velocidad terminal es la misma que la velocidad límite, que es la velocidad del objeto que cae después de que ha transcurrido un tiempo (relativamente) largo.
De manera similar, la distancia límite del barco es la distancia que recorrerá el barco después de que haya transcurrido un largo período de tiempo. Debido a las propiedades de decaimiento exponencial, el tiempo requerido para alcanzar cualquiera de estos valores no es demasiado largo (¡ciertamente no es una cantidad infinita de tiempo!) Pero se encuentran rápidamente llevando el límite al infinito.
 Comprueba tu aprendizaje 6.11
Comprueba tu aprendizaje 6.11
Video
Observa el siguiente vídeo
Para terminar este apartado, te invitamos a que observes el siguiente objeto interactivo, diseñado por Juan Guillermo Rivera Berrío, publicado en su libro Métodos Numéricos. Se trata del problema clásico del descenso de un paracaidista y el cálculo de la velocidad límite o terminal.
Trabajo y energía
cinética
En 1702, viviendo en Londres y sirviendo como Maestro de la Casa de la Moneda, Newton posó para Godfrey Kneller, el retratista más famoso y probablemente el más caro de Londres. Para este retrato usó un banyan rojo y una peluca suelta (Smithsonian Record ID: edanmdm:nmah_1452104).
Introducción

En este capítulo, discutimos algunos conceptos físicos básicos involucrados en cada movimiento físico en el universo, iremos más allá de los conceptos de fuerza y cambio en movimiento, que discutimos en cinemática y dinámica. Estos conceptos son trabajo, energía cinética y potencia. Explicamos cómo estas cantidades se relacionan entre sí, lo que nos llevará a una relación fundamental llamada el teorema del trabajo y energía.
En el próximo capítulo, generalizamos esta idea al principio más amplio de la conservación de la energía.
La aplicación de las leyes de Newton generalmente requiere resolver ecuaciones diferenciales que relacionan las fuerzas que actúan sobre un objeto con las aceleraciones que producen.
A menudo, una solución analítica es intratable o imposible, y requiere soluciones numéricas largas o simulaciones para obtener resultados aproximados.
En tales situaciones, las relaciones más generales, como el teorema del trabajo y energía (o la conservación de la energía), aún pueden proporcionar respuestas útiles a muchas preguntas y requieren una cantidad más modesta de cálculo matemático. En particular, verás cómo el teorema energía-trabajo es útil para relacionar las velocidades de una partícula, en diferentes puntos a lo largo de su trayectoria, con las fuerzas que actúan sobre ella, incluso cuando la trayectoria es demasiado complicada de manejar. Por lo tanto, algunos aspectos del movimiento se pueden abordar con menos ecuaciones y sin descomposiciones de vectores.
Trabajo
En física, se trabaja en un objeto cuando la energía se transfiere al objeto. En otras palabras, el trabajo se realiza cuando una fuerza actúa sobre algo que sufre un desplazamiento de una posición a otra. Las fuerzas pueden variar en función de la posición, y los desplazamientos pueden ser a lo largo de varios caminos entre dos puntos. Primero definimos el incremento del trabajo $dW$ hecho por una fuerza $\bold{\vec{F}}$ que actúa a través de un desplazamiento infinitesimal $d\bold{\vec{r}}$ como el producto escalar de estos dos vectores:
Luego, podemos sumar las contribuciones para desplazamientos infinitesimales, a lo largo de una ruta entre dos posiciones, para obtener el trabajo total.
El trabajo realizado por una fuerza es la integral de la fuerza con respecto al desplazamiento a lo largo de la ruta o trayectoria del desplazamiento:
$$W_{AB} = \int_{\text{ruta AB}} \bold{\vec{F}}\cdot d\bold{\vec{r}}\tag{7.2}$$
Los vectores implicados en la definición del trabajo realizado por una fuerza que actúa sobre una partícula se ilustran en la Figura 7.2.
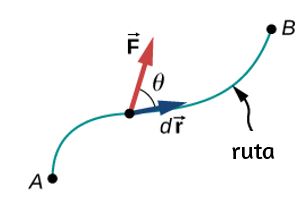
Elegimos expresar el producto punto en términos de la magnitud de los vectores y el coseno del ángulo entre ellos, porque el significado del producto escalar para el trabajo se puede expresar en palabras más directamente en términos de magnitudes y ángulos.
Igualmente podríamos haber expresado el producto punto en términos de los diversos componentes introducidos en los Vectores. En dos dimensiones, estos fueron los componentes $x$ e $y$ en coordenadas cartesianas, o los componentes $r$ y $\phi$ en coordenadas polares; en tres dimensiones, solo eran los componentes $x-, y-$ y $z-$. Cuál opción es más conveniente depende de la situación. En palabras, puedes expresar la ecuación 7.1 para el trabajo realizado por una fuerza que actúa sobre un desplazamiento como producto de un componente que actúa en paralelo al otro componente. A partir de las propiedades de los vectores, no importa si se toma el componente de la fuerza paralelo al desplazamiento o el componente del desplazamiento paralelo a la fuerza; se obtiene el mismo resultado de cualquier manera.
Recuerda que la magnitud de una fuerza por el coseno del ángulo que hace la fuerza con una dirección dada es la componente de la fuerza en la dirección dada. Los componentes de un vector pueden ser positivos, negativos o cero, dependiendo de si el ángulo entre el vector y la dirección del componente está entre $0\degree$ y $90\degree$ o $90\degree$ y $180\degree$, o es igual a $90\degree$. Como resultado, el trabajo realizado por una fuerza puede ser positivo, negativo o cero, dependiendo de si la fuerza está en la dirección del desplazamiento, opuesta al desplazamiento, o perpendicular al desplazamiento. El trabajo máximo se realiza con una fuerza dada cuando está en la dirección del desplazamiento $(cos\theta = \pm 1)$, y el trabajo cero se realiza cuando la fuerza es perpendicular al desplazamiento $(cos\theta = 0)$.
Las unidades de trabajo son unidades de fuerza multiplicadas por unidades de longitud, que en el sistema SI son newtons multiplicados por metros, $N\cdot m$. Esta combinación se llama joule, por razones históricas que mencionaremos más adelante, y se abrevia como $J$.
En el sistema inglés, aún utilizado en los Estados Unidos, la unidad de fuerza es la libra ($lb$) y la unidad de distancia es el pie ($ft$), por lo que la unidad de trabajo es el pie-libra ($ft\cdot lb$).
Trabajo realizado por fuerzas constantes y fuerzas de contacto
El trabajo más simple de evaluar es el realizado por una fuerza que es constante en magnitud y dirección. En este caso, podemos restar importancia a la fuerza; la integral resultante es solo el desplazamiento total, que solo depende de los puntos finales $A$ y $B$, pero no de la ruta entre ellos:
$$W_{AB} = \bold{\vec{F}} \int_A^B d\bold{\vec{r}} = \bold{\vec{F}}\cdot (\bold{\vec{r}}_B -\bold{\vec{r}}_A) = |\bold{\vec{F}}||\bold{\vec{r}}_B - \bold{\vec{r}}_A|cos\theta$$También podemos ver esto escribiendo la Ecuación 7.2 en coordenadas cartesianas y usando el hecho de que las componentes de la fuerza son constantes:
$$\begin{split} W_{AB} &= \int_{\text{ruta AB}} \bold{\vec{F}} d\bold{\vec{r}} = \int_{\text{ruta AB}} (F_x dx + F_y dy + F_z dz)\\ &= F_x\int_A^B dx + F_y\int_A^B dy + F_z\int_A^B dz\\ &= F_x(x_B − x_A) + F_y(y_B − y_A) + F_z(z_B − z_A)\\ &= \bold{\vec{F}}\cdot (\bold{\vec{r}}_B − \bold{\vec{r}}_A) \end{split}$$La Figura 7.3 (a) muestra a una persona ejerciendo una fuerza constante $\bold{\vec{F}}$ a lo largo del mango de una cortadora de césped, que forma un ángulo $\theta$ con la horizontal. El desplazamiento horizontal del cortacésped, sobre el que actúa la fuerza, es $\bold{\vec{d}}$.
El trabajo realizado en la cortadora de césped es $W = \bold{\vec{F}}\cdot \bold{\vec{d}} = Fdcos\theta$, que la figura también ilustra como la componente horizontal de la fuerza multiplicada por la magnitud del desplazamiento.
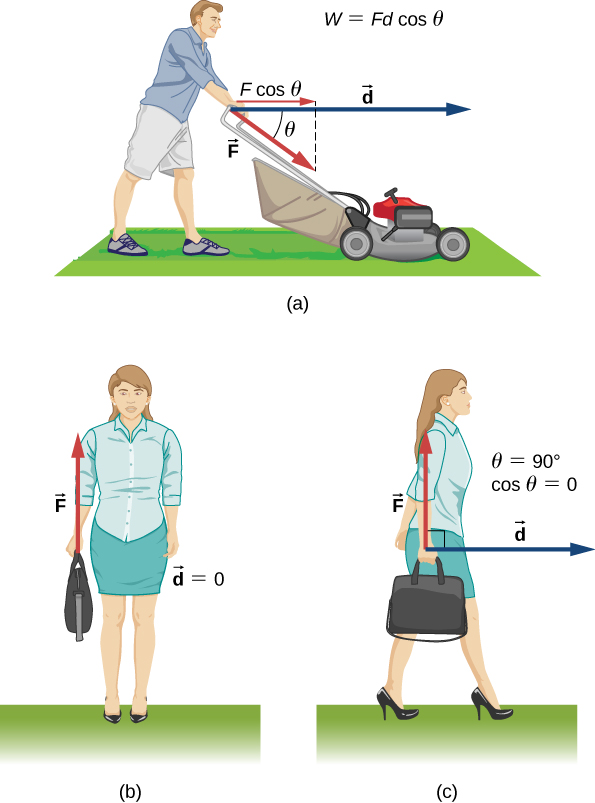
La Figura 7.3 (b) muestra a una persona sosteniendo un maletín. La persona debe ejercer una fuerza ascendente, igual en magnitud al peso del maletín, pero esta fuerza no funciona, porque el desplazamiento sobre el que actúa es cero. Entonces, ¿por qué finalmente te sientes cansado solo con sostener el maletín, si no estás trabajando en eso? La respuesta es que las fibras musculares de tu brazo se contraen y trabajan dentro de tu brazo, a pesar de que la fuerza que tus músculos ejercen externamente en el maletín no funciona (Parte de la fuerza que ejerces también puede ser tensión en los huesos y ligamentos de tu brazo, pero otros músculos en tu cuerpo estarían trabajando para mantener la posición de tu brazo).
En la Figura 7.3 (c), donde la persona en (b) camina horizontalmente con velocidad constante, el trabajo realizado por la persona en el maletín sigue siendo cero, pero ahora porque el ángulo entre la fuerza ejercida y el desplazamiento es $90\degree$ ($\bold{\vec{F}}$ es perpendicular a $\bold{\vec{d}}$) y $cos90\degree = 0$.
Ejemplo 7.1
Calculando el trabajo para empujar una cortadora de césped
¿Cuánto trabajo realiza la persona en la podadora de césped en la figura Figura 7.3 (a) si ejerce una fuerza constante de $75.0 N$ en un ángulo de $35\degree$ por debajo de la horizontal y empuja la podadora a $25.0 m$ sobre una superficie nivelada?
Estrategia
Podemos resolver este problema sustituyendo los valores dados en la definición de trabajo realizado en un objeto por una fuerza constante, expresada en la ecuación $W = Fdcos\theta$. La fuerza, el ángulo y el desplazamiento se dan, por lo que solo el trabajo $W$ es desconocido.
Solución
La ecuación para el trabajo es
$$W = Fdcos\theta$$Sustituyendo:
$$W = (75.0 N)(25.0 m)cos(35.0\degree) = 1.54\times 10^3 J$$Explicación
Pese a que uno y medio de kilojulio puede parecer mucho trabajo, veremos en Energía potencial y Conservación de energía que solo se trata de trabajar tanto como se puede quemar un sexto de un gramo de grasa.
Cuando cortas el pasto, otras fuerzas actúan sobre el cortacésped además de la fuerza que ejerces, es decir, la fuerza de contacto del suelo y la fuerza gravitatoria de la Tierra. Consideremos el trabajo realizado por estas fuerzas en general. Para un objeto que se mueve sobre una superficie, el desplazamiento $d\bold{\vec{r}}$ es tangente a la superficie. La parte de la fuerza de contacto en el objeto que es perpendicular a la superficie es la fuerza normal $\bold{\vec{N}}$. Como el coseno del ángulo entre la normal y la tangente a una superficie es cero, tenemos
$$dW_N = \bold{\vec{N}}\cdot d\bold{\vec{r}} = \bold{\vec{0}}$$La fuerza normal nunca funciona en estas circunstancias (Ten en cuenta que si el desplazamiento $\bold{\vec{r}}$ tuviera una componente relativa perpendicular a la superficie, el objeto abandonaría la superficie o la rompería, y ya no existiría ninguna fuerza de contacto normal.
Sin embargo, si el objeto es más que una partícula, y tiene una estructura interna, la fuerza de contacto normal puede trabajar en ella, por ejemplo, al desplazarla o deformarla (esto se mencionará en el próximo capítulo).
La parte de la fuerza de contacto en el objeto que es paralela a la superficie es la fricción, $\bold{\vec{f}}$. Para que este objeto se deslice por la superficie, la fricción cinética $\bold{\vec{f}}_k$ es opuesta a $d\bold{\vec{r}}$, con respecto a la superficie, por lo que el trabajo realizado por la fricción cinética es negativo. Si la magnitud de $\bold{\vec{f}}_k$ es constante (como lo sería si todas las otras fuerzas en el objeto fueran constantes), entonces el trabajo hecho por fricción es
donde $|lAB|$ es la longitud del camino en la superficie (ten en cuenta que, especialmente si el trabajo realizado por una fuerza es negativo, las personas pueden referirse al trabajo realizado contra esta fuerza, donde $dW_{\text{en contra}} = -dW_{\text{a favor}}$. El trabajo realizado contra una fuerza también puede verse como el trabajo requerido para superar esta fuerza, como en "¿Cuánto trabajo se requiere para superar ...?"). La fuerza de fricción estática, sin embargo, puede hacer un trabajo positivo o negativo. Cuando caminas, la fuerza de fricción estática ejercida por el suelo sobre tu pie trasero te acelera por una parte de cada paso. Si estás disminuyendo la velocidad, la fuerza del suelo sobre tu pie delantero te desacelera. Si conduces tu automóvil al límite de velocidad en un tramo recto y nivelado de la carretera, el trabajo negativo realizado por la fricción cinética de la resistencia del aire se equilibra con el trabajo positivo realizado por la fricción estática de la carretera en las ruedas.
Puedes sacar la alfombra de debajo de un objeto de tal forma que se deslice hacia atrás con respecto a la alfombra, pero hacia adelante con respecto al piso.
En este caso, la fricción cinética ejercida por la alfombra sobre el objeto podría estar en la misma dirección que el desplazamiento del objeto, en relación con el piso, y hacer un trabajo positivo. La conclusión es que debes analizar cada caso particular para determinar el trabajo realizado por las fuerzas, ya sea positivo, negativo o cero.
Ejemplo 7.2
Moviendo un sofá
Decides mover tu sofá a una nueva posición en el piso de tu sala de estar. La fuerza normal en el sofá es $1 kN$ y el coeficiente de fricción es $0.6$. (a) Primero empuja el sofá 3 m paralelos a una pared y luego $1 m $perpendicular a la pared ($A$ a $B$ en la Figura 7.4). ¿Cuánto trabajo se realiza por la fuerza de fricción? (b) No te gusta la nueva posición, por lo que mueves el sofá directamente a su posición original ($B$ a $A$ en la Figura 7.4). ¿Cuál fue el trabajo total realizado contra la fricción al mover el sofá de su posición original y viceversa?
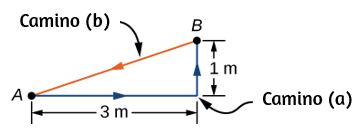
Estrategia
La magnitud de la fuerza de fricción cinética en el sofá es constante, igual al coeficiente de fricción multiplicado por la fuerza normal, $f_k = \mu_kN$.
Por lo tanto, el trabajo que hace es $W_{fr} = -f_k d$, donde $d$ es la longitud de la ruta atravesada. Los segmentos de las rutas son los lados de un triángulo rectángulo, por lo que las longitudes de ruta se calculan fácilmente. En la parte (b), puedes usar el hecho de que el trabajo realizado contra una fuerza es el resultado negativo del trabajo realizado por la fuerza.
Solución
a. El trabajo hecho por fricción es
$$W = −(0.6)(1 kN)(3 m + 1 m) = −2.4kJ$$b. La longitud del camino a lo largo de la hipotenusa es de $\sqrt{10} m$, por lo que el trabajo total realizado contra la fricción es
$$W = (0.6)(1 kN)(3 m + 1 m + \sqrt{10} m) = 4.3kJ$$Explicación
El camino total sobre el cual se evaluó el trabajo de fricción comenzó y terminó en el mismo punto (era un camino cerrado), de modo que el desplazamiento total del sillón era cero. Sin embargo, el trabajo total no fue cero. La razón es que fuerzas como la fricción se clasifican como fuerzas no conservativas o fuerzas disipativas, como veremos en el próximo capítulo.
 Comprueba tu aprendizaje 7.1
Comprueba tu aprendizaje 7.1
La otra fuerza en el cortacésped mencionada anteriormente era la fuerza gravitacional de la Tierra o el peso de la podadora. Cerca de la superficie de la Tierra, la fuerza gravitacional sobre un objeto de masa m tiene una magnitud constante, mg, y dirección constante, verticalmente hacia abajo. Por lo tanto, el trabajo hecho por la gravedad sobre un objeto es el producto punto de su peso y su desplazamiento. En muchos casos, es conveniente expresar el producto escalar para el trabajo gravitatorio en términos de los componentes $x, y$ y $z$. Un sistema de coordenadas típico tiene el eje $x$ horizontal y el eje y vertical. Entonces la fuerza gravitatoria es $-mg\^{\bold{j}}$, por lo que el trabajo hecho por la gravedad, en cualquier camino de $A$ a $B$, es
El trabajo realizado por una fuerza de gravedad constante sobre un objeto depende únicamente del peso del objeto y la diferencia de altura a través de la cual se desplaza el objeto. La gravedad funciona negativamente en un objeto que se mueve hacia arriba $(y_B \gt y_A)$, o, en otras palabras, debes hacer un trabajo positivo contra la gravedad para levantar un objeto hacia arriba. Alternativamente, la gravedad hace un trabajo positivo en un objeto que se mueve hacia abajo $(y_B \gt y_A)$, o haces un trabajo negativo contra la gravedad para "levantar" un objeto hacia abajo, controlando su descenso para que no caiga al suelo. ("Levante" se usa en lugar de "soltar").
Ejemplo 7.3
Estanterías de un libro
Levanta un libro de la biblioteca sobredimensionado, que pesa $20 N$, $1 m$ verticalmente desde un estante, y lo llevas $3 m$ horizontalmente a una mesa (Figura 7.5). ¿Cuánto trabajo hace la gravedad en el libro? (b) Cuando hayas terminado, mueve el libro en línea recta a su lugar original en el estante. ¿Cuál fue el trabajo total realizado contra la gravedad, alejando el libro de su posición original en el estante y viceversa?
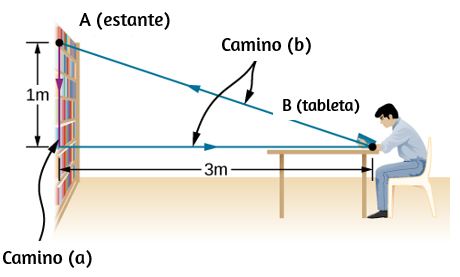
Estrategia
Acabamos de ver que el trabajo realizado por una fuerza de gravedad constante depende únicamente del peso del objeto movido y la diferencia de altura para el camino tomado, $W_{AB} = -mg (y_B - y_A)$. Podemos evaluar la diferencia de altura para responder (a) y (b).
Solución
a. Como el libro comienza en el estante y se baja $y_B - y_A = -1 m$, tenemos
$$W = - (20 N)(- 1 m) = 20J$$b. Hay una diferencia de altura cero para cualquier ruta que comience y termine en el mismo lugar en el estante, entonces $W = 0$.
Explicación
La gravedad hace un trabajo positivo ($20 J$) cuando el libro baja del estante. La fuerza gravitacional entre dos objetos es una fuerza atractiva, que hace un trabajo positivo cuando los objetos se acercan. La gravedad no funciona ($0 J$) cuando el libro se mueve horizontalmente del estante a la mesa y el trabajo negativo ($-20 J$) cuando el libro se mueve de la mesa al estante. El trabajo total realizado por gravedad es cero $[20J + 0J + (- 20J) = 0]$. A diferencia de la fricción u otras fuerzas de disipación, descritas en el ejemplo 7.2, el trabajo total realizado contra la gravedad, sobre cualquier trayectoria cerrada, es cero. El trabajo positivo se realiza contra la gravedad en las partes ascendentes de un camino cerrado, pero se realiza una cantidad igual de trabajo negativo contra la gravedad en las partes descendentes. En otras palabras, el trabajo realizado contra la gravedad, levantar un objeto hacia arriba, se "devuelve" cuando el objeto vuelve a bajar. Fuerzas como la gravedad (aquellas que hacen cero el trabajo sobre cualquier camino cerrado) se clasifican como fuerzas conservadoras y juegan un papel importante en la física.
 Comprueba tu aprendizaje 7.2
Comprueba tu aprendizaje 7.2
El trabajo realizado por las fuerzas que varían
En general, las fuerzas pueden variar en magnitud y dirección en puntos en el espacio, y las trayectorias entre dos puntos pueden ser curvas. El trabajo infinitesimal realizado por una fuerza variable se puede expresar en términos de los componentes de la fuerza y el desplazamiento a lo largo de la trayectoria,
$$dW = F_xdx + F_ydy + F_zdz$$Aquí, los componentes de la fuerza son funciones de posición a lo largo de la trayectoria, y los desplazamientos dependen de las ecuaciones de la trayectoria (aunque elegimos ilustrar dW en coordenadas cartesianas, otras coordenadas se adaptan mejor a algunas situaciones). La ecuación 7.2 define el trabajo total como una integral de línea, o el límite de una suma de cantidades infinitesimales de trabajo. El concepto físico de trabajo es sencillo: calcula el trabajo para desplazamientos pequeños y los suma. Algunas veces las matemáticas pueden parecer complicadas, pero el siguiente ejemplo demuestra cuán limpiamente pueden operar.
Ejemplo 7.4
Trabajo realizado por una fuerza variable sobre un camino curvo
Un objeto se mueve a lo largo de una trayectoria parabólica $y = (0.5 m^{-1}x^2$ desde el origen $A = (0,0)$ hasta el punto $B = (2 m, 2 m )$ bajo la acción de una fuerza $\bold{\vec{F}} = (5 N/m)y\^{\bold{i}} + (10 N/m)x\^{\bold{j}}$ (Figura 7.6) . Calcula el trabajo realizado.
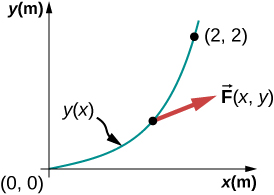
Estrategia
Los componentes de la fuerza tienen funciones de $x$ e $y$. Podemos usar la ecuación de la trayectoria para expresar $y$ y $dy$ en términos de $x$ y $dx$; a saber,
$$y = (0.5 m^{-1}>)x^2\;\;\, y \;\;\;dy = 2(0.5 m^{-1})xdx$$Entonces, la integral para el trabajo es solo una integral definida de una función de $x$.
Solución
El elemento de trabajo infinitesimal es
$$dW = F_xdx + F_ydy = (5 N/m)ydx + (10 N/m)xdy$$La integral de $x^2$ es $x^3/3$, entonces:
$$\begin{split} W &= \int_0^{2m}(12.5 N/m^2)x^2dx = (12.5 N/m^2)\frac{x^3}{3}\Big]_0^{2m}\\ &= (12.5 N/m^2)\Big(\frac83\Big) = 33.3 J \end{split}$$Explicación
Esta integral no fue difícil de calcular. Puedes seguir los mismos pasos, como en este ejemplo, para calcular integrales de línea que representan el trabajo para fuerzas y trayectorias más complicadas. En este ejemplo, todo fue dado en términos de componentes $x$ e $y$, que son los más fáciles de usar al evaluar el trabajo en este caso. En otras situaciones, las magnitudes y los ángulos pueden ser más fáciles.
 Comprueba tu aprendizaje 7.3
Comprueba tu aprendizaje 7.3
Una fuerza variable muy importante y ampliamente aplicable es la fuerza ejercida por un resorte perfectamente elástico, que cumple la ley de Hooke $\bold{\vec{F}} = -k\Delta \bold{\vec{x}}$, donde $k$ es la constante de resorte, y $\Delta\bold{\vec{x}} = \bold{\vec{x}} - \bold{\vec{x}}_{eq}$ es el desplazamiento desde la posición no estirada (equilibrio) del resorte (Leyes de movimiento de Newton).
Ten en cuenta que la posición no estirada es solo la misma que la posición de equilibrio si no están actuando otras fuerzas (o, si lo están, se cancelan entre sí). Las fuerzas entre las moléculas, o en cualquier sistema que experimenta pequeños desplazamientos desde un equilibrio estable, se comportan aproximadamente como una fuerza de resorte.
Para calcular el trabajo realizado por una fuerza de resorte, podemos elegir el eje $x$ a lo largo del resorte, en la dirección de aumento de longitud, como en la Figura 7.7, con el origen en la posición de equilibrio $x_{eq} = 0$ (entonces $x$ positivo corresponde a un estiramiento y $x$ negativo a compresión). Con esta elección de coordenadas, la fuerza del resorte tiene solo un componente $x, F_x = -kx$, y el trabajo realizado cuando x cambia de $x_A$ a $x_B$ es
Observa que $W_{AB}$ depende solo de los puntos inicial y final, $A$ y $B$, y es independiente de la ruta real entre ellos, siempre que comience en $A$ y termine en $B$. Es decir, la ruta real podría implicar ir y venir antes de terminar.
Otra cosa interesante de notar sobre la Ecuación 7.5 es que, para este caso unidimensional, puedes ver fácilmente la correspondencia entre el trabajo realizado por una fuerza y el área bajo la curva de la fuerza versus su desplazamiento. Recuerda que, en general, una integral unidimensional es el límite de la suma de infinitesimales, $f(x)dx$, que representa el área de franjas, como se muestra en la Figura 7.8.
En la ecuación 7.5, como $F = -kx$ es una línea recta con pendiente $-k$, cuando se representa con respecto a $x$, el "área" debajo de la línea es solo una combinación algebraica de "áreas" triangulares, donde "áreas" encima del eje $x$ son positivos y los de abajo son negativos, como se muestra en la Figura 7.9. La magnitud de una de estas "áreas" es solo la mitad de la base del triángulo, a lo largo del eje x, multiplicado por la altura del triángulo, a lo largo del eje de la fuerza. (Hay comillas alrededor de "área" porque este producto de altura base tiene las unidades de trabajo, en lugar de metros cuadrados).
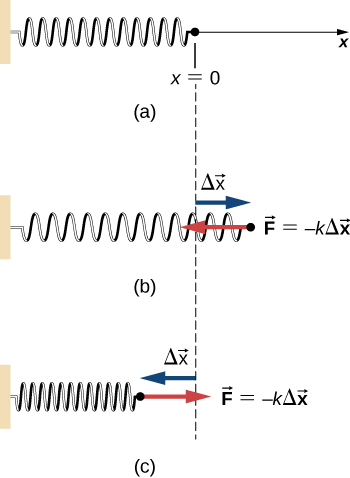
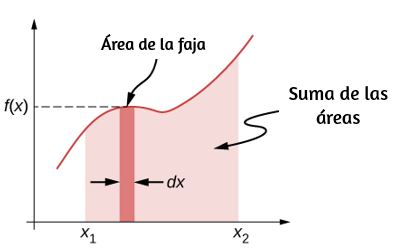
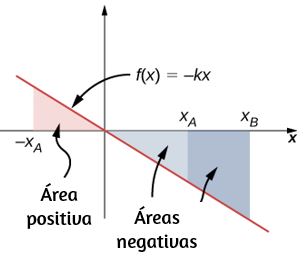
Ejemplo 7.5
Trabajo realizado por la fuerza del resorte
Un resorte perfectamente elástico requiere 0.54 J de trabajo para estirar 6 cm desde su posición de equilibrio, como en la Figura 7.7 (b). (a) ¿Cuál es su constante de resorte $k$? (b) ¿Cuánto trabajo se requiere para estirarlo $6 cm$ adicionales?
Estrategia
Trabajo "requerido" significa trabajo realizado contra la fuerza del resorte, que es el resultado negativo del trabajo en la Ecuación 7.5, que es
$$W = \frac12 k(x_B^2 - x_A^2)$$Para la parte (a), $x_A = 0$ y $x_B = 6cm$; para la parte (b), $x_A = 6 cm$ y $x_B = 12 cm$. En la parte (a), se da el trabajo y se puede resolver por la constante del resorte; en la parte (b), puedes usar el valor de $k$, de la parte (a), para calcular el trabajo.
Solución
a. $W = 0.54 J = \frac12 k[(6 cm)^2 - 0]$, luego $k = 3 N/cm$.
b. $W = \frac12 (3 N/cm)[(12 cm)^2 - (6 cm)^2] = 1,62 J$
Explicación
Como el trabajo realizado por una fuerza de resorte es independiente de la ruta, solo se necesita calcular la diferencia en la cantidad $\frac12 kx^2$ en los puntos finales.
Ten en cuenta que el trabajo requerido para estirar el resorte de $0$ a $12 cm$ es cuatro veces el requerido para estirarlo de $0$ a $6 cm$, porque ese trabajo depende del cuadrado de la cantidad de estiramiento desde el equilibrio, $\frac12 kx^2$. En esta circunstancia, el trabajo para estirar el resorte de $0$ a $12 cm$ también es igual al trabajo para un camino compuesto de $0$ a $6 cm$ seguido de un tramo adicional de $6 cm\;\;a \;\;12 cm$. Por lo tanto, $4W(0 cm\;\; a \;\;6 cm) = W(0 cm \;\;a \;\;6 cm) + W (6 cm \;\;a \;\;12 cm)$, o $W(6 cm \;\;a \;\;12 cm) = 3W(0 cm \;\;a\;\; 6cm)$ como lo encontramos antes.
 Comprueba tu aprendizaje 7.4
Comprueba tu aprendizaje 7.4
Para terminar este apartado, practica con el objeto interactivo de la página siguiente, diseñado por Oscar Escamilla González. El interactivo permite que el alumno compare diferentes modelos e identifique sus características.
Energía cinética
Es plausible suponer que cuanto mayor sea la velocidad de un cuerpo, mayor será el efecto que podría tener en otros cuerpos. Esto no depende de la dirección de la velocidad, solo de su magnitud. A finales del siglo XVII, se introdujo una cantidad en la mecánica para explicar las colisiones entre dos cuerpos perfectamente elásticos, en los que un cuerpo choca de frente con un cuerpo idéntico en reposo.
El primer cuerpo se detiene y el segundo cuerpo se mueve con la velocidad inicial del primer cuerpo. (Si alguna vez jugaste al billar o al croquet, o si has visto un modelo de Newton's Cradle, has observado este tipo de colisión). La idea detrás de esta cantidad estaba relacionada con las fuerzas que actuaban sobre un cuerpo y se refería a "la energía de movimiento". Más tarde, durante el siglo dieciocho, el nombre de energía cinética se le dio a la energía del movimiento.
Con esta historia en mente, ahora podemos establecer la definición clásica de energía cinética. Ten en cuenta que cuando decimos "clásico", nos referimos a no-relativista, es decir, a velocidades mucho menores que la velocidad de la luz. A velocidades comparables a la velocidad de la luz, la teoría especial de la relatividad requiere una
expresión diferente para la energía cinética de una partícula, como se analiza en Relatividad.
Dado que los objetos (o sistemas) de interés varían en complejidad, primero definimos la energía cinética de una partícula con masa $m$.
La energía cinética de una partícula es la mitad del producto de la masa $m$ de la partícula y el cuadrado de su velocidad $v$: $$K = \frac12 mv^2\tag{7.6}$$
Luego, ampliamos esta definición a cualquier sistema de partículas sumando las energías cinéticas de todas las partículas constituyentes:
Observa que así como podemos expresar la segunda ley de Newton en términos de la tasa de cambio de momento o masa multiplicada por el cambio de velocidad, entonces la energía cinética de una partícula se puede expresar en términos de su masa y momento ($\bold{\vec{p}} = m\bold{\vec{v}}$), en lugar de su masa y velocidad. Luego, $v = p/m$, vemos que
$$K = \frac12 m\Big(\frac{p}{m}\Big)^2 = \frac{p^2}{2m}$$también expresa la energía cinética de una sola partícula. A veces, esta expresión es más conveniente de usar que la ecuación 7.6.
Las unidades de energía cinética son masa multiplicada por el cuadrado de velocidad, o $kg\cdot m^2/s^2$. Pero las unidades de fuerza son tiempos de aceleración masivos, $kg\cdot m/s^2$, entonces las unidades de energía cinética son también las unidades de fuerza por distancia, que son las unidades de trabajo, o joules. Verás en la siguiente sección que el trabajo y la energía cinética tienen las mismas unidades, porque son formas diferentes de la misma propiedad física más general.
Ejemplo 7.6
Energía Cinética de un Objeto
(a) ¿Cuál es la energía cinética de un atleta de 80 kg, que corre a $10 m/s$?
(b) Se cree que el cráter Chicxulub en Yucatán, uno de los mayores cráteres de impacto existentes en la Tierra, fue creado por un asteroide que viajaba a $22 km/s$ y liberando $4.2 \times 10^{23} J$ de energía cinética en el momento del impacto. ¿Cuál era su masa? (c) En los reactores nucleares, los neutrones térmicos, que viajan a aproximadamente $2.2 km/s$, juegan un papel importante. ¿Cuál es la energía cinética de tal partícula?
Estrategia
Para responder estas preguntas, puedes usar la definición de energía cinética en la Ecuación 7.6. También debes buscar la masa de un neutrón.
Solución
No olvides convertir $km$ en $m$ para hacer estos cálculos, aunque, para ahorrar espacio, omitimos mostrar estas conversiones.
a. $K = \frac12 (80 kg)(10 m/s)^2 = 4.0 kJ$.
b. $m = 2K/v^2 = 2(4.2\times 10^{23} J)/(22 km/s)^2 = 1.7\times 10^{15} kg$
c. $K = \frac12 (1.68×10^{-27} kg)(2.2 km/s)^2 = 4.1\times 10^{-21} J$
Explicación
En este ejemplo, utilizamos la forma en que la masa y la velocidad están relacionadas con la energía cinética, y encontramos una gama muy amplia de valores para las energías cinéticas. Diferentes unidades se usan comúnmente para valores muy grandes y muy pequeños.
La energía del impacto del asteroide en la parte (b) se puede comparar con el del explosivo de TNT y las explosiones nucleares, $1 megaton = 4,18 \times 10^{15} J$. La energía cinética del asteroide Chicxulub era de unos cien millones de megatones. En el otro extremo, la energía de la partícula subatómica se expresa en electrón-voltios, $1eV = 1.6 \times 10^{-19} J$. El neutrón térmico en la parte (c) tiene una energía cinética de aproximadamente una cuadragésima parte de un electrón-voltio.
Como la velocidad es una cantidad relativa, puedes ver que el valor de la energía cinética debe depender de su marco de referencia. En general, puedes elegir un marco de referencia que sea adecuado para el propósito de su análisis y que simplifique sus cálculos. Uno de esos marcos de referencia es aquel en el que se realizan las observaciones del sistema (probablemente un marco externo).
Otra opción es un marco que se adjunta o se mueve con el sistema (probablemente un marco interno). Las ecuaciones para movimiento relativo, discutidas anteriormente, proporcionan un enlace para calcular la energía cinética de un objeto con respecto a diferentes marcos de referencia.
Ejemplo 7.7
Energía cinética relativa a diferentes marcos de referencia
Una persona de $75.0 kg$ camina por el pasillo central de un vagón de metro a una velocidad de $1.50 m/s$ con respecto al vagón, mientras que el tren se mueve a $15.0 m/s$ con respecto a las vías. (a) ¿Cuál es la energía cinética de la persona en relación con el vagón? (b) ¿Cuál es la energía cinética de la persona en relación con las pistas? (c) ¿Cuál es la energía cinética de la persona en relación con un marco que se mueve con la persona?
Estrategia
Como se dan velocidades, podemos usar $\frac12 mv^2$ para calcular la energía cinética de la persona. Sin embargo, en la parte (a), la velocidad de la persona es relativa al vagón del metro (tal como se da); en la parte (b), es relativo a las vías; y en la parte (c), es cero. Si denotamos el marco del vagón por $C$, el marco de las pistas por $T$, y la persona por $P$, las velocidades relativas en la parte (b) están relacionadas por $\bold{\vec{v}}_{PT}= \bold{\vec{v}}_{PC} + \bold{\vec{v}}_{CT}$. Podemos suponer que el pasillo central y las vías se encuentran en la misma línea, pero no se especifica la dirección en la que la persona camina en relación con el vagón, por lo que daremos una respuesta para cada posibilidad, $v_{PT} = v_{CT} \pm v_{PC}$, como se muestra en la Figura 7.10.

Solución
a. $K = \frac12 (75.0 kg)(1.50 m/s)^2 = 84.4 J$.
b. $v_{PT} = (15.0 \pm 1.50)m/s$. Por lo tanto, los dos valores posibles para la energía cinética en relación con el vagón son:
y
$$K = \frac12 (75.0 kg)(16.5 m/s)^2 = 10.2 kJ$$c. En un marco donde $v_P = 0$, también $K = 0$.
Explicación
Puedes ver que la energía cinética de un objeto puede tener valores muy diferentes, según el marco de referencia. Sin embargo, la energía cinética de un objeto nunca puede ser negativa, ya que es el producto de la masa y el cuadrado de la velocidad, que son siempre positivos o cero.
 Comprueba tu aprendizaje 7.6
Comprueba tu aprendizaje 7.6
La energía cinética de una partícula es una cantidad única, pero la energía cinética de un sistema de partículas a veces se puede dividir en varios tipos, dependiendo del sistema y su movimiento.
Por ejemplo, si todas las partículas en un sistema tienen la misma velocidad, el sistema está experimentando movimiento de traslación y tiene energía cinética de traslación. Si un objeto está girando, podría tener energía cinética de rotación, o si está vibrando, podría tener energía cinética de vibración. La energía cinética de un sistema, en relación con un marco de referencia interno, puede llamarse energía cinética interna. La energía cinética asociada con el movimiento molecular aleatorio se puede llamar energía térmica. Independientemente del nombre, cada tipo de energía cinética es la misma cantidad física, que representa la energía asociada con el movimiento.
Ejemplo 7.8
Nombres especiales para la energía cinética
(a) Un jugador lanza un pase en mitad de la cancha con una pelota de básquetbol de $624 g$, que cubre $15 m$ en $2 s$. ¿Cuál es la energía cinética de traslación horizontal del balón durante el vuelo? (b) Una molécula de aire, dentro del balón en la parte (a), tiene una masa de $29 u$, y una velocidad promedio de $500 m/s$, en relación con el balón.
Hay alrededor de $3 \times 10^{23}$ moléculas dentro de él, moviéndose en direcciones aleatorias, cuando la pelota está correctamente inflada. ¿Cuál es la energía cinética de traslación promedio del movimiento aleatorio de todas las moléculas en el interior, en relación con el balón? (c) ¿Qué tan rápido tendría que viajar la pelota de baloncesto en relación con la cancha, como en la parte (a), para tener una energía cinética igual a la cantidad en la parte (b)?
Estrategia
En la parte (a), primero encuentra la velocidad horizontal del balón y luego usa la definición de energía cinética en términos de masa y velocidad, $K = \frac12 mv^2$.
Luego, en la parte (b), convierte las unidades unificadas en kilogramos y luego usa $K = \frac12 mv^2$ para obtener la energía cinética de traslación promedio de una molécula, en relación con el balón. Luego, multiplica por el número de moléculas para obtener el resultado total. Finalmente, en la parte (c), podemos sustituir la cantidad de energía cinética en la parte (b), y la masa del balón en la parte (a), en la definición $K = \frac12 mv^2$, y hallar $v$.
Solución
a. La velocidad horizontal es $(15 m)/(2 s)$, por lo que la energía cinética horizontal del baloncesto es
$$\frac12 (0.624 kg)(7.5 m/s)^2 = 17.6 J$$b. La energía cinética de traslación promedio de una molécula es
$$\frac12 (29u)(1.66 \times 10^{-27} kg/u)(500 m/s)^2 = 6.02 \times 10^{-21} J$$y la energía cinética total de todas las moléculas es
$$(3 \times 10^{23})(6.02 \times 10^{-21} J) = 1.80 kJ$$c. $v = \sqrt{2(1.8 kJ)/(0.624 kg)} = 76.0 m/s$
Explicación
En la parte (a), este tipo de energía cinética se puede llamar la energía cinética horizontal de un objeto (la pelota de baloncesto), en relación con su entorno (la cancha). Si la pelota de baloncesto estuviera girando, todas las partes de ella no solo tendrían la velocidad promedio, sino que también tendría energía cinética de rotación. La parte (b) nos recuerda que este tipo de energía cinética se puede llamar energía cinética interna o térmica. Ten en cuenta que esta energía es aproximadamente cien veces la energía de la parte (a). Cómo hacer uso de la energía térmica será el tema de la termodinámica. En la parte (c), dado que la energía en la parte (b) es aproximadamente $100$ veces mayor que en la parte (a), la velocidad debe ser aproximadamente $10$ veces mayor, lo que es ($76$ comparado con $7.5 m/s$).
Teorema del trabajo-energía
Hemos discutido cómo encontrar el trabajo realizado en una partícula por las fuerzas que actúan sobre ella, pero ¿cómo se manifiesta ese trabajo en el movimiento de la partícula? De acuerdo con la segunda ley del movimiento de Newton, la suma de todas las fuerzas que actúan sobre una partícula, o la fuerza neta, determina la tasa de cambio en el momento de la partícula, o su movimiento. Por lo tanto, debemos considerar el trabajo realizado por todas las fuerzas que actúan sobre una partícula, o la red de trabajo, para ver qué efecto tiene sobre el movimiento de la partícula.
Comencemos mirando el trabajo neto realizado en una partícula mientras se mueve sobre un desplazamiento infinitesimal, que es el producto punto de la fuerza neta y el desplazamiento: $dW_{neto} = \bold{\vec{F}}_{neta}\cdot d\bold{\vec{r}}$. La segunda ley de Newton nos dice que $\bold{\vec{F}}_{neta} = m(d\bold{\vec{v}}/dt)$, entonces $dW_{neta} = m(d\bold{\vec{v}}/dt)\cdot d\bold{\vec{r}}$. Para las funciones matemáticas que describen el movimiento de una partícula física, podemos reordenar los diferenciales dt, etc., como cantidades algebraicas en esta expresión, es decir,
$$dW_{neto} = m\Big(\frac{d\bold{\vec{v}}}{dt}\Big)\cdot \bold{\vec{r}} = md\bold{\vec{v}}\cdot\Big(\frac{d\bold{\vec{r}}}{dt}\Big) = m\bold{\vec{v}}\cdot d\bold{\vec{v}}$$donde sustituimos la velocidad por la derivada con respecto al tiempo del desplazamiento y usamos la propiedad conmutativa del producto punto [Ecuación 2.30]. Dado que las derivadas e integrales de los escalares probablemente te resulten más familiares en este punto, expresamos el producto punto en términos de coordenadas cartesianas antes de integrar entre dos puntos A y B en la trayectoria de la partícula. Esto nos da el trabajo neto hecho en la partícula:
En el paso intermedio, usamos el hecho de que el cuadrado de la velocidad es la suma de los cuadrados de sus componentes cartesianos, y en el último paso usamos la definición de la energía cinética de la partícula. Este importante resultado se llama el teorema del trabajo-energía (Figura 7.11).
El trabajo neto hecho en una partícula es igual al cambio en la energía cinética de la partícula: $$W_{neto} = K_B - K_A\tag{7.9}$$

De acuerdo con este teorema, cuando un objeto se ralentiza, su energía cinética final es menor que su energía cinética inicial, el cambio en su energía cinética es negativo, y también lo es el trabajo neto realizado en él. Si un objeto se acelera, el trabajo neto realizado en él es positivo.
Al calcular el trabajo, debes incluir todas las fuerzas que actúan sobre un objeto. Si omites las fuerzas que actúan sobre un objeto, o si incluyes cualquier fuerza que no actúe sobre él, obtendrás un resultado incorrecto.
La importancia del teorema del trabajo-energía, y las generalizaciones adicionales a las que conduce, es que hace que algunos tipos de cálculos sean mucho más simples de lo que lo serían al tratar de resolver la segunda ley de Newton.
Por ejemplo, en la Leyes del movimiento de Newton, encontramos la velocidad de un objeto que se desliza por un plano sin fricción al resolver la segunda ley de Newton para la aceleración y el uso de ecuaciones cinemáticas para la aceleración constante, obteniendo
$$v_f^2 = v_i^2 + 2g(s_f − s_i)sen\theta$$donde $s$ es el desplazamiento por el plano.
También podemos obtener este resultado del teorema del trabajo-energía. Dado que solo dos fuerzas están actuando sobre el objeto -la gravedad y la fuerza normal- y, la fuerza normal no hace ningún trabajo, el trabajo en red es solo el trabajo realizado por la gravedad. Esto solo depende del peso del objeto y la diferencia de altura, por lo que
$$W_{neto} = W_{grav} = −mg(y_f − y_i)$$donde $y$ es positivo hacia arriba. El teorema del trabajo-energía dice que esto equivale al cambio en la energía cinética:
$$-mg(y_f − y_i) = \frac12 m(v_f^2 - v_i^2)$$Utilizando un triángulo rectángulo, podemos ver que $(y_f − y_i) = (s_f − s_i) sen\theta$, por lo que el resultado para la velocidad final es el mismo.
¿Qué se gana al usar el teorema del trabajo-energía? La respuesta es que para una superficie plana sin fricción, no mucho.
Sin embargo, la segunda ley de Newton es fácil de resolver solo para este caso particular, mientras que el teorema del trabajo-energía da la velocidad final para cualquier superficie sin fricción. Para una superficie curva arbitraria, la fuerza normal no es constante, y la segunda ley de Newton puede ser difícil o imposible de resolver analíticamente. Constante o no, para el movimiento a lo largo de una superficie, la fuerza normal nunca funciona, porque es perpendicular al desplazamiento. Un cálculo que usa el teorema trabajo-energía evita esta dificultad y se aplica a situaciones más generales.
- Dibuja un diagrama de cuerpo libre para cada fuerza en el objeto.
- Determina si cada fuerza funciona o no sobre el desplazamiento en el diagrama. Asegúrate de mantener los signos positivos o negativos en el trabajo realizado.
- Suma la cantidad total de trabajo realizado por cada fuerza.
- Establece este trabajo total igual al cambio en la energía cinética y halla cualquier parámetro desconocido.
- Comprueba tus respuestas. Si el objeto viaja a velocidad constante o aceleración cero, el trabajo total realizado debe ser cero y coincidir con el cambio en la energía cinética. Si el trabajo total es positivo, el objeto debe haber acelerado o aumentado la energía cinética. Si el trabajo total es negativo, el objeto debe haber disminuido o disminuido la energía cinética.
Ejemplo 7.9
Rizar el rizo
La pista sin fricción para un coche de juguete incluye un loop-the-loop de radio $R$. ¿Qué altura, medida desde el fondo del circuito, debe colocarse el automóvil para comenzar desde el reposo en la sección de la vía y recorrer todo el rizo?
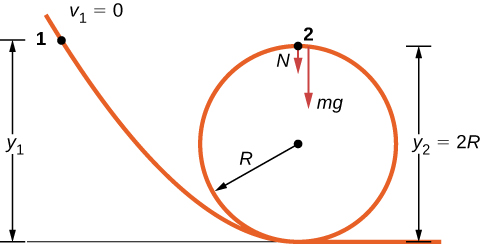
Estrategia
El diagrama de cuerpo libre en la posición final del objeto se dibuja en la Figura 7.12. El trabajo gravitatorio es el único trabajo realizado sobre el desplazamiento que no es cero. Como el peso apunta en la misma dirección que el desplazamiento vertical neto, el trabajo total realizado por la fuerza gravitacional es positivo. Del teorema del trabajo-energía, la altura de inicio determina la velocidad del automóvil en la parte superior del circuito,
$$mg(y_2 − y_1) = \frac12 mv_2^2$$donde la notación se muestra en la figura adjunta. En la parte superior del ciclo, la fuerza y la gravedad normales están bajas y la aceleración es centrípeta, por lo que
$$a_{top} = \frac{F}{m} = \frac{N + mg}{m} = \frac{v_2^2}{R}$$La condición para mantener el contacto con la pista es que debe haber alguna fuerza normal, por leve que sea; es decir, $N \gt 0$. Sustituyendo $v_2^2$ y $N4, podemos encontrar la condición para $y_1$.
Solución
Implementa los pasos en la estrategia para llegar al resultado deseado:
$$N = \frac{-mg - mv_2^2}{R} = \frac{-mg + 2mg(y_1 - 2R)}{R}\gt 0\;\;\; o \;\;\;y_1 \gt \frac{5R}{2}$$Explicación
En la superficie del circuito, el componente normal de la gravedad y la fuerza de contacto normal deben proporcionar la aceleración centrípeta del automóvil que circula por el circuito. El componente tangencial de la gravedad ralentiza o acelera el automóvil. Un niño descubriría qué tan alto arrancar el automóvil por prueba y error, pero ahora que conoce el teorema del trabajo-energía, puede predecir la altura mínima (así como otros resultados más útiles) de los principios físicos. Al usar el teorema del trabajo-energía, no tuviste que resolver una ecuación diferencial para determinar la altura.
 Comprueba tu aprendizaje 7.7
Comprueba tu aprendizaje 7.7
En situaciones donde se conoce el movimiento de un objeto, pero no se conocen los valores de una o más de las fuerzas que actúan sobre él, se puede usar el teorema de trabajo-energía para obtener información sobre las fuerzas. El trabajo depende de la fuerza y la distancia sobre la que actúa, por lo que la información se proporciona a través de su producto.
Ejemplo 7.10
Determinando una fuerza de parada
Una bala de un cartucho de calibre 0.22LR tiene una masa de $40$ granos ($2.60 g$) y una velocidad de salida de $1100 ft/s$ ($335 m/s$).
Puede penetrar ocho tableros de pino de 1 pulgada, cada uno con un espesor de $0,75$ pulgadas. ¿Cuál es la fuerza de frenado o de parada promedio ejercida por la madera, como se muestra en la Figura 7.13?
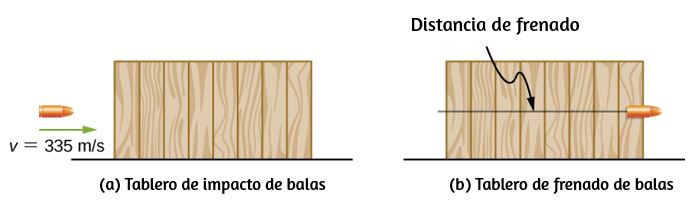
Estrategia
Podemos suponer que bajo las condiciones generales indicadas, la bala pierde toda su energía cinética penetrando las tablas, por lo que el teorema del trabajo-energía dice que su energía cinética inicial es igual a la fuerza de parada promedio por la distancia que penetró. El cambio en la energía cinética de la bala y el trabajo neto hecho deteniéndolo son ambos negativos, así que cuando escribes el teorema de trabajo-energía, con el trabajo neto igual a la fuerza promedio por la distancia de parada, eso es lo que obtienes. El espesor total de ocho tablas de pino de 1 pulgada que penetra la bala es de $8 \times \frac34$ pulgadas = $6$ pulgadas = $15,2 cm$.
Solución
Aplicando el teorema del trabajo-energía, obtenemos
$$W_{neta} = -F_{prom}\Delta s_{parada} = -K_{inicial}$$así que
$$F_{prom} = \frac{1/2mv^2}{\Delta s_{parada}} = \frac{0.5(0.0026 kg)(335 m/s)^2}{0.152 m} = 960N$$Explicación
Podríamos haber usado la segunda ley y la cinemática de Newton en este ejemplo, pero el teorema del trabajo-energía también proporciona una respuesta a situaciones menos simples. La penetración de una bala, disparada verticalmente hacia arriba en un bloque de madera, se analiza en una sección del artículo de Asif Shakur ["Bullet-Block Science Video Puzzle". The Physics Teacher (enero de 2015) 53 (1): 15-16 ]. Si la bala se dispara en el centro muerto en el bloque, pierde toda su energía cinética y penetra un poco más lejos que si se dispara fuera del centro. La razón es que si la bala impacta descentrada, tiene un poco de energía cinética después de que deja de penetrar, porque el bloque gira. El teorema del trabajo-energía implica que un cambio menor en la energía cinética da como resultado una penetración más pequeña. Comprenderás más de la física en este interesante artículo después de que termines de leer el apartado sobre Momentum Angular.
Potencia
El concepto de trabajo implica fuerza y desplazamiento; el teorema del trabajo-energía relaciona el trabajo neto hecho en un cuerpo con la diferencia en su energía cinética, calculada entre dos puntos en su trayectoria. Ninguna de estas cantidades o relaciones implica tiempo explícitamente, sin embargo, sabemos que el tiempo disponible para realizar una determinada cantidad de trabajo con frecuencia es tan importante para nosotros como la cantidad misma.
En la figura de apertura de este capítulo, varios velocistas pudieron haber alcanzado la misma velocidad en el final, y por lo tanto hicieron la misma cantidad de trabajo, pero el ganador de la carrera lo hizo en la menor cantidad de tiempo.
Expresamos la relación entre el trabajo realizado y el intervalo de tiempo involucrado en hacerlo, al introducir el concepto de potencia. Como el trabajo puede variar como una función del tiempo, primero definimos la potencia promedio como el trabajo realizado durante un intervalo de tiempo, dividido por el intervalo,
Entonces, podemos definir la potencia instantánea (a menudo denominada simplemente potencia).
La potencia se define como la tasa de trabajo, o el límite de la potencia promedio para intervalos de tiempo que se aproximan a cero, $$P = \frac{dW}{dt}\tag{7.11}$$
Si la potencia es constante durante un intervalo de tiempo, la potencia promedio para ese intervalo es igual a la potencia instantánea, y el trabajo realizado por el agente que suministra la potencia es $W = P\Delta t$:
El teorema del trabajo-energía relaciona cómo el trabajo puede transformarse en energía cinética. Como también hay otras formas de energía, como veremos en el próximo capítulo, también podemos definir la potencia como la tasa de transferencia de energía. El trabajo y la energía se miden en unidades de julios, por lo que la potencia se mide en unidades de julios por segundo, a la que se le ha dado el nombre en el SI de watts, abreviado como $W$: $1 J/s = 1 W$. Otra unidad común para expresar la capacidad de potencia de los dispositivos cotidianos es la potencia: $1 hp$ (caballo de fuerza) = $746 W$.
Ejemplo 7.11
Potencia de levantamiento
Un aprendiz del ejército de $80 kg$ hace $10$ ejercicios de levantamiento en barra en $10 s$ (Figura 7.14). ¿Cuánta energía promedio suministran los músculos del aprendiz moviendo su cuerpo? (Sugerencia: haz estimaciones razonables para cualquier cantidad necesaria).
Estrategia
El trabajo realizado contra la gravedad, subir o bajar una distancia $\Delta_y$, es $mg\Delta_y$. (Si te levantas y bajas a velocidad constante, la fuerza que ejerces cancela la gravedad durante todo el ciclo de levantamiento). Por lo tanto, el trabajo realizado por los músculos del aprendiz (moviendo, pero no acelerando, su cuerpo) para una repetición completa (arriba y abajo) es $2mg\Delta_y$.
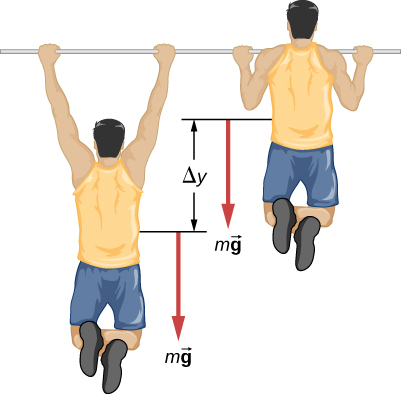
Supongamos que $\Delta_y = 2ft \approx 60cm$. Además, supón que los brazos comprenden el $10\%$ de la masa corporal y no están incluidos en la masa en movimiento. Con estas suposiciones, podemos calcular el trabajo realizado para $10$ levantamientos y dividir entre $10 s$ para obtener la potencia promedio.
Solución
$$P_{prom} = \frac{10\times 2(0.9\times 80kg)(9.8m/s^2)(0.6m)}{10 s} = 850 W$$Explicación
Esto es típico para el gasto de energía en ejercicios extenuantes; en unidades diarias es algo más que un caballo de fuerza ($1hp = 746W$).
 Comprueba tu aprendizaje 7.8
Comprueba tu aprendizaje 7.8
La potencia involucrada en mover un cuerpo también se puede expresar en términos de las fuerzas que actúan sobre él. Si una fuerza $\bold{\vec{F}}$ actúa sobre un cuerpo desplazado $d\bold{\vec{r}}$ en un tiempo $dt$, la potencia gastada por la fuerza es
$$P = \frac{dW}{dt} = \frac{\bold{\vec{F}}\cdot d\bold{\vec{r}}}{dt} = \bold{\vec{F}}\cdot \Big(\frac{d\bold{\vec{r}}}{dt}\Big) = \bold{\vec{F}}\cdot \bold{\vec{v}}$$donde $\bold{\vec{v}}$ es la velocidad del cuerpo. El hecho de que los límites implicados por las derivadas existen, para el movimiento de un cuerpo real, justifica la reorganización de los infinitesimales.
Ejemplo 7.12
Potencia automotriz cuesta arriba
¿Cuánta potencia debe gastar un motor de automóvil para mover un auto de $1200 kg$ en una pendiente del $15\%$ a $90 km/h$ (Figura 7.15)? Supón que el 25% de esta potencia se disipa superando la resistencia del aire y la fricción.
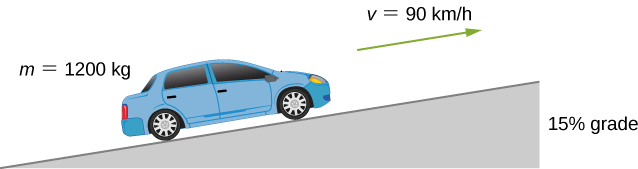
Estrategia
A velocidad constante, no hay cambio en la energía cinética, por lo que el trabajo neto realizado para mover el automóvil es cero. Por lo tanto, la potencia suministrada por el motor para mover el automóvil es igual a la potencia gastada contra la gravedad y la resistencia del aire. Por supuesto, el $75\%$ de la potencia se suministra contra la gravedad, que es igual a $m\bold{\vec{g}}\cdot \bold{\vec{v}} = mgvsen\theta$, donde $\theta$ es el ángulo de la inclinación. Una pendiente del $15\%$ significa $tan\theta = 0.15$. Este razonamiento nos permite hallar la potencia requerida.
Solución
Llevando a cabo los pasos sugeridos, encontramos
$$0.75P = mgvsen(tan^{−1}0.15),$$ $$P = \frac{(1200 \times 9.8N)(90m/3.6s)sen(8.53\degree)}{0.75} = 58kW$$alrededor de $78 hp$ (debes saber los pasos utilizados para convertir unidades).
Explicación
Esta es una cantidad razonable de energía para el motor de un automóvil pequeño o mediano ($1 hp = 0.746 kW$). Ten en cuenta que esta es solo la potencia gastada para mover el automóvil. Gran parte de la potencia del motor se destina a otro lado, por ejemplo, al calor residual. Es por eso que los autos necesitan radiadores. Cualquier potencia restante podría usarse para la aceleración o para operar los accesorios del automóvil.

Energía potencial y
conservación de la energía
Video publicado en TikTok, en el canal @spacialist_
Introducción

En la escultura de bolas de George Rhoads, el principio de la conservación de la energía rige los cambios en la energía cinética de la bola y los relaciona con los cambios y las transferencias de otros tipos de energía asociados con las interacciones de la bola. En este capítulo, presentamos el importante concepto de energía potencial. Esto nos permitirá formular la ley de conservación de energía mecánica y aplicarla a sistemas simples, facilitando la resolución de problemas.
En la sección final sobre fuentes de energía, consideraremos las transferencias de energía y la ley general de conservación de la energía. A lo largo de este libro, la ley de la conservación de la energía se aplicará cada vez con más detalle, a medida que te encuentres con sistemas más complejos y variados, y con otras formas de energía.
Hemos visto que el trabajo realizado sobre un objeto por la constante de la fuerza gravitacional, cerca de la superficie de la Tierra, sobre cualquier desplazamiento es una función relacionada con la diferencia de las posiciones de los puntos finales del desplazamiento. Esta propiedad nos permite definir un tipo diferente de energía para el sistema, que se llama energía potencial. Consideramos varias propiedades y tipos de energía potencial en las siguientes subsecciones.
Energía potencial de un sistema
En el capítulo anterior, vimos que el trabajo realizado sobre un objeto por la constante de la fuerza gravitacional, cerca de la superficie de la Tierra, sobre cualquier desplazamiento es una función solamente de la diferencia en las posiciones de los puntos finales del desplazamiento. Esta propiedad nos permite definir un tipo diferente de energía para el sistema, que se llama energía potencial. Consideramos varias propiedades y tipos de energía potencial en las siguientes subsecciones.
Conceptos básicos de energía potencial
En el capítulo sobre movimiento en dos y tres dimensiones, analizamos el movimiento de un proyectil, como patear un balón de fútbol en la Figura 8.2. Para este ejemplo, ignoremos la fricción y la resistencia del aire. A medida que la pelota se eleva, el trabajo realizado por la fuerza de gravedad en la pelota es negativo, porque el desplazamiento de la pelota es positivo verticalmente y la fuerza debida a la gravedad es negativa en sentido vertical.
También notamos que la pelota disminuyó su velocidad hasta que alcanzó su punto más alto en el movimiento, disminuyendo así la energía cinética.
Esta pérdida de energía cinética se traduce en una ganancia en energía potencial gravitacional del sistema pelota-Tierra.
A medida que la pelota cae hacia la Tierra, el trabajo realizado en la pelota ahora es positivo, porque tanto el desplazamiento como la fuerza gravitatoria apuntan verticalmente hacia abajo. La pelota también se acelera, lo que indica un aumento en la energía cinética. Por lo tanto, la energía se convierte de energía potencial gravitacional en energía cinética.
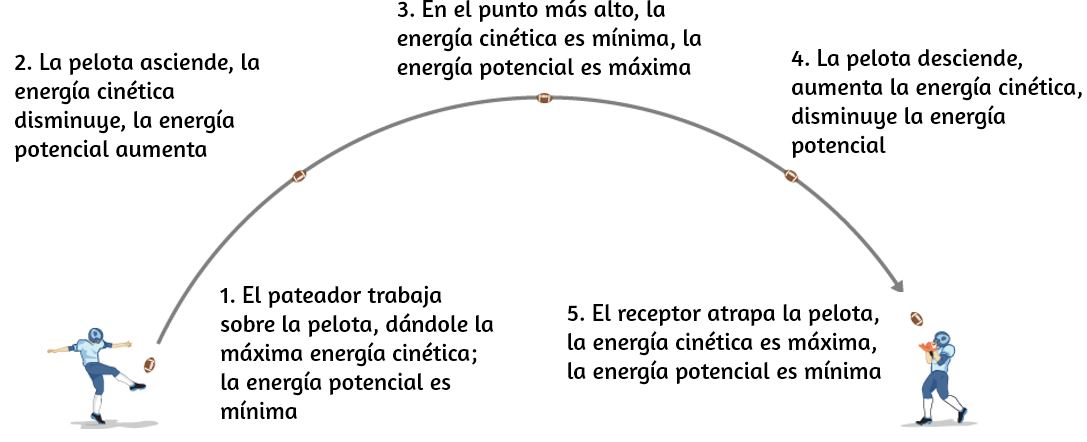
Con base en este escenario, podemos definir la diferencia de energía potencial del punto $A$ al punto $B$ como el resultado negativo del trabajo realizado:
Esta fórmula establece explícitamente una diferencia de energía potencial, no solo una energía potencial absoluta.
Por lo tanto, necesitamos definir la energía potencial en una posición dada de tal manera que establezca valores estándar de energía potencial por sí mismos, en lugar de diferencias de energía potenciales. Hacemos esto reescribiendo la función de energía potencial en términos de una constante arbitraria,
La elección de la energía potencial en una ubicación inicial de $\bold{\vec{r}}_0$ se realiza por conveniencia en el problema dado. Lo más importante, cualquiera que sea la elección que se haga, debe establecerse y mantenerse constante durante todo el problema. Hay algunas elecciones bien aceptadas de energía potencial inicial. Por ejemplo, la altura más baja en un problema generalmente se define como energía potencial cero, o si un objeto está en el espacio, el punto más alejado del sistema a menudo se define como energía potencial cero. Entonces, la energía potencial, con respecto a cero en $\bold{\vec{r}}_0$, es simplemente $U(\bold{\vec{r}})$.
Mientras no haya fricción o resistencia del aire, el cambio en la energía cinética de la pelota equivale al cambio en la energía potencial gravitatoria de la pelota. Esto se puede generalizar a cualquier energía potencial:
Veamos un objeto interactivo, diseñado por José Luis Abreu León y Carlos Alberto Jaimes Vergara.
En este interactivo puedes observar las relaciones de la energía cinética con la velocidad y la energía potencial con la altura y, además, desarrollar una idea intuitiva sobre los conceptos de energía cinética y energía potencial y su conservación a través de la simulación de las transformaciones de energía en una montaña rusa.
Veamos, ahora, un ejemplo específico, eligiendo cero para energía potencial gravitacional en puntos convenientes.
Ejemplo 8.1
Propiedades Básicas de la Energía Potencial
Una partícula se mueve a lo largo del eje $x$ bajo la acción de una fuerza dada por $F = -ax^2$, donde $a = 3 N/m^2$.
(a) ¿Cuál es la diferencia en su energía potencial cuando se mueve de $x_A = 1 m$ a $x_B = 2 m$? (b) ¿Cuál es la energía potencial de la partícula en $x = 1 m$ con respecto a una dada de $0.5 J$ de energía potencial en $x = 0$?
Estrategia
(a) La diferencia en la energía potencial es el negativo del trabajo realizado, como se define en la ecuación 8.1. El trabajo se define en el capítulo anterior como el producto punto de la fuerza por la distancia. Dado que la partícula se mueve hacia adelante en la dirección x, el producto escalar se simplifica a una multiplicación ($\^{\bold{i}}\cdot \^{\bold{i}} = 1$). Para encontrar el trabajo total realizado, necesitamos integrar la función entre los límites dados. Después de la integración, podemos establecer el trabajo o la energía potencial. (b) La función de energía potencial, con respecto a cero en $x = 0$, es la integral indefinida encontrada en la parte (a), con la constante de integración determinada a partir de la ecuación 8.3. Luego, sustituimos el valor $x$ en la función de energía potencial para calcular la energía potencial en $x = 1m$.
Solución
a. El trabajo realizado por la fuerza dada a medida que la partícula se mueve desde la coordenada $x$ a $x + dx$ en una dimensión es
$$dW = \bold{\vec{F}}\cdot d\bold{\vec{r}} = Fdx = -ax^2dx$$Sustituyendo la expresión anterior en la Ecuación 8.1, obtenemos
$$\Delta U = -W = \int_{x_1}^{x_2} ax^2dx = \frac13 (3 N/m^2)x^2\Big] _{2m}^{1m} = 7 J$$b. La integral indefinida para la función de energía potencial en la parte (a) es
$$U(x) = \frac13 ax^3 + \text{ constante}$$y queremos que la constante sea determinada por
$$U(0) = 0.5 J$$Por lo tanto, la energía potencial con respecto a cero en $x = 0$ es solo
$$U(x) = \frac13 ax^3 + 0.5 J$$Por lo tanto, la energía potencial en $x = 1 m$ es
$$U(1 m) = \frac13 (3 N/m^2)(1 m)^3 + 0.5 J = 1.5 J$$Explicación
En este ejemplo unidimensional, cualquier función que podamos integrar, independientemente de la ruta, es conservadora. Observa cómo aplicamos la definición de diferencia de energía potencial para determinar la función de energía potencial con respecto a cero en un punto elegido.
También nota que la energía potencial, como se determina en la parte (b), en $x = 1m$ es $U(1m) = 1 J$ y en $x = 2m$ es $U(2m) = 8J$; su diferencia es el resultado en la parte (a).
 Comprueba tu aprendizaje 8.1
Comprueba tu aprendizaje 8.1
Sistemas de varias partículas
En general, un sistema de interés podría consistir en varias partículas. La diferencia en la energía potencial del sistema es el resultado negativo del trabajo realizado por las fuerzas gravitatorias o elásticas, que, como veremos en la siguiente sección, son fuerzas conservadoras. La diferencia de energía potencial depende solo de las posiciones inicial y final de las partículas, y de algunos parámetros que caracterizan la interacción (como la masa para la gravedad o la constante del resorte para la fuerza según la ley de Hooke).
Es importante recordar que la energía potencial es una propiedad de las interacciones entre objetos en un sistema elegido, y no solo una propiedad de cada objeto.
Esto es especialmente cierto para las fuerzas eléctricas, aunque en los ejemplos de energía potencial que consideramos a continuación, las partes del sistema son tan grandes (como la Tierra, en comparación con un objeto en su superficie) o tan pequeñas (como un manantial sin masa), los cambios que sufren esas partes son insignificantes si se incluyen en el sistema.
Tipos de energía potencial
Para cada tipo de interacción presente en un sistema, puedes etiquetar un tipo correspondiente de energía potencial.
La energía potencial total del sistema es la suma de las energías potenciales de todos los tipos (esto se desprende de la propiedad aditiva del producto punto en la expresión del trabajo realizado). Veamos algunos ejemplos específicos de tipos de energía potencial. Primero, consideramos cada una de estas fuerzas cuando actúan por separado, y luego cuando ambas actúan juntas.
Energía potencial gravitacional cerca de la superficie de la Tierra
El sistema de interés consiste en nuestro planeta, la Tierra y una o más partículas cerca de su superficie (o cuerpos lo suficientemente pequeños para ser considerados como partículas, en comparación con la Tierra). La fuerza gravitacional en cada partícula (o cuerpo) es solo su peso mg cerca de la superficie de la Tierra, actuando verticalmente hacia abajo. De acuerdo con la tercera ley de Newton, cada partícula ejerce una fuerza en la Tierra de igual magnitud pero en la dirección opuesta. La segunda ley de Newton nos dice que la magnitud de la aceleración producida por cada una de estas fuerzas en la Tierra es mg dividida por la masa de la Tierra.
Como la relación de la masa de cualquier objeto ordinario con la masa de la Tierra es extremadamente pequeña, el movimiento de la Tierra puede ser completamente despreciado. Por lo tanto, consideramos que este sistema es un grupo de sistemas de partículas individuales, sujetos a la fuerza gravitacional uniforme de la Tierra.
El trabajo realizado en un cuerpo por la fuerza gravitacional uniforme de la Tierra, cerca de su superficie, depende de la masa del cuerpo, la aceleración debida a la gravedad y la diferencia de altura recorrida por el cuerpo, como lo indica la Ecuación 7.4. Por definición, este trabajo es el negativo de la diferencia en la energía potencial gravitacional, por lo que la diferencia es
De esto se puede ver que la función de la energía potencial gravitacional, cerca de la superficie de la Tierra, es
Puedes elegir el valor de la constante, como se describe en la discusión de la Ecuación 8.2; sin embargo, para resolver la mayoría de los problemas, la constante más conveniente para elegir es cero para cuando $y = 0$, que es la posición vertical más baja en el problema.
Ejemplo 8.2
Energía potencial gravitacional de un excursionista
La cima del Great Blue Hill en Milton, MA, está $147 m$ por encima de su base y tiene una elevación sobre el nivel del mar de $195 m$ (Figura 8.3) (Su nombre nativo americano, Massachusett, fue adoptado por los colonos por nombrar la colonia de la bahía y el estado cerca de su ubicación). Un excursionista de $75 kg$ asciende desde la base hasta la cumbre.
¿Cuál es la energía potencial gravitacional del sistema excursionista-Tierra con respecto a la energía potencial gravitatoria cero en la altura de la base, cuando el excursionista está (a) en la base de la colina, (b) en la cumbre y (c) en el nivel del mar?

Estrategia
Primero, necesitamos elegir un origen para el eje $y$ y luego determinar el valor de la constante que hace que la energía potencial sea cero a la altura de la base. Entonces, podemos determinar las energías potenciales a partir de la ecuación 8.5, en función de la relación entre la altura de energía potencial cero y la altura a la que se encuentra el caminante.
Solución
Vamos a elegir el origen para el eje y en la altura de la base, donde también queremos que el cero de energía potencial esté. Esta elección hace que la constante sea igual a cero y
$$U(base) = U(0) = 0$$En la cima $y = 147m$, entonces
$$U(cumbre) = U(147 m) = mgh = (75 × 9.8 N)(147 m) = 108 kJ$$A nivel del mar, $y = (147-195) m = -48m$, entonces
$$U(nivel del mar) = (75 \times 9.8 N)(- 48 m) = - 35.3k J$$Explicación
Además de ilustrar el uso de la Ecuación 8.4 y la Ecuación 8.5, los valores de energía potencial gravitacional que encontramos son razonables. La energía potencial gravitacional es más alta en la cima que en la base, y más baja en el nivel del mar que en la base. La gravedad también te funciona en tu camino hacia arriba. Haz un trabajo negativo y no tanto (en magnitud), como lo hacen tus músculos. Pero ciertamente funciona. Del mismo modo, tus músculos trabajan en tu camino hacia abajo, como trabajo negativo. Los valores numéricos de las energías potenciales dependen de la elección del cero de la energía potencial, pero las diferencias físicamente significativas de la energía potencial no lo hacen (Ten en cuenta que dado que la Ecuación 8.2 es una diferencia, los valores numéricos no dependen del origen de las coordenadas).
 Comprueba tu aprendizaje 8.2
Comprueba tu aprendizaje 8.2
Energía potencial elástica
En el capítulo anterior, vimos que el trabajo realizado por un resorte perfectamente elástico, en una dimensión, depende solo de la constante de resorte y de los cuadrados de los desplazamientos desde la posición no estirada, como se muestra en la Ecuación 7.5. Este trabajo involucra solo las propiedades de la interacción de la ley de Hooke y no las propiedades de resortes reales y cualquier objeto que se les atribuya.
Por lo tanto, podemos definir la diferencia de energía potencial elástica para una fuerza de resorte como el negativo del trabajo realizado por la fuerza de resorte en esta ecuación, antes de considerar los sistemas que incorporan este tipo de fuerza. Así,
donde el objeto viaja del punto $A$ al punto $B$. La función de energía potencial correspondiente a esta diferencia es
Si la fuerza del resorte es la única fuerza que actúa, es más simple tomar el cero de la energía potencial en $x = 0$, cuando el resorte está en su longitud no estirada. Entonces, la constante es la ecuación 8.7 es cero (otras opciones pueden ser más convenientes si otras fuerzas están actuando).
Ejemplo 8.3
Energía potencial de un resorte
Un sistema contiene un resorte perfectamente elástico, con una longitud no estirada de $20 cm$ y una constante de resorte de $4 N/cm$. (a) ¿Cuánta energía potencial elástica aporta el resorte cuando su longitud es de $23 cm$? (b) ¿Cuánta energía potencial adicional contribuye si su longitud aumenta a $26 cm$?
Estrategia
Cuando el resorte está en su longitud no estirada, no contribuye en nada a la energía potencial del sistema, por lo que podemos usar la Ecuación 8.7 con la constante igual a cero. El valor de $x$ es la longitud menos la longitud no estirada. Cuando se expande el resorte, el desplazamiento del resorte o la diferencia entre su longitud relajada y su longitud estirada deben usarse para el valor de $x$ al calcular la energía potencial del resorte.
Solución
a. El desplazamiento del resorte es $x = 23cm - 20cm = 3cm$, por lo que la energía potencial aportada es $U = \frac12 kx^2 = \frac12 (4 N/cm)(3cm)^2 = 0.18J$.
b. Cuando el desplazamiento del resorte es $x = 26cm - 20cm = 6cm$, la energía potencial es $U = \frac12 kx^2 = \frac12 (4 N/cm)(6cm)^2 = 0.72 J$, que es un aumento de $0.54 J$ sobre la cantidad en la parte (a).
Explicación
El cálculo de la energía potencial elástica y las diferencias de energía potencial de la ecuación 8.7 implica la solución de las energías potenciales en función de las longitudes dadas del resorte.
Como $U$ depende de $x^2$, la energía potencial para una compresión ($x$ negativo) es la misma que para una extensión de igual magnitud.
 Comprueba tu aprendizaje 8.3
Comprueba tu aprendizaje 8.3
Energía potencial gravitacional y elástica
Un sistema simple que incorpora ambos tipos de energía potencial gravitacional y elástica es un sistema vertical de masa unidimensional. Consiste en una partícula (o bloque) masiva, colgada de un extremo de un resorte sin masa perfectamente elástico, el otro extremo del cual está fijo, como se ilustra en la figura 8.4.
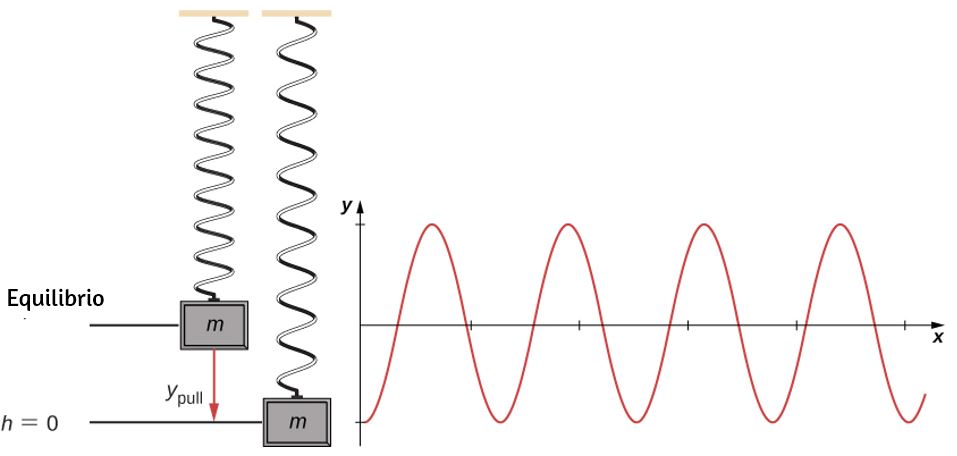
Primero, consideremos la energía potencial del sistema. Suponiendo que el resorte no tenga masa, el sistema del bloque-Tierra gana y pierde energía potencial. Necesitamos definir la constante en la función de energía potencial de la Ecuación 8.5. A menudo, el suelo es una elección adecuada para cuando la energía potencial gravitacional es cero; sin embargo, en este caso, el punto más bajo o cuando $h = 0$ es una ubicación conveniente para la energía potencial gravitacional cero.
Ten en cuenta que esta elección es arbitraria, y el problema se puede resolver correctamente incluso si se elige otra opción. También debemos definir la energía potencial elástica del sistema y la constante correspondiente, como se detalla en la ecuación 8.7. La ubicación de equilibrio es la más adecuada matemáticamente para elegir donde la energía potencial del resorte es cero.
Por lo tanto, de acuerdo con esta convención, cada energía potencial y energía cinética se puede escribir para tres puntos críticos del sistema: (1) el punto más bajo, (2) la posición de equilibrio del resorte, y (3) el punto más alto logrado. Observamos que la energía total del sistema se conserva, por lo que cualquier energía total en este gráfico podría combinarse para resolver una cantidad desconocida. Los resultados se muestran en la Tabla 8.1.
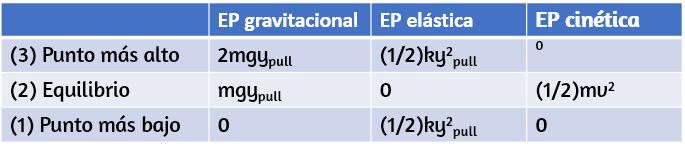

En la siguiente simulación , diseñada por Michael Gallis y modificada por Anne J Cox (Modelo de energía bungee), se muestra una prueba de salto bungee ficticio desde una torre.
En la simulación se muestra un maniquí de prueba saltando desde una torre, se registra la energía cinética, la energía potencial gravitacional y la energía potencial elástica del bungee.
¡Haz clic en el botón de la esquina superior derecha, para ampliar la escena!
Ejemplo 8.4
Energía potencial de un sistema vertical de masa-resorte
Un bloque que pesa $12 N$ se cuelga de un resorte con una constante de resorte de $6.0 N/m$, como se muestra en la Figura 8.4. El bloque se baja unos $5,0 cm$ adicionales de su posición de equilibrio y se libera. (a) ¿Cuál es la diferencia solo en la energía potencial del resorte, desde una posición de equilibrio inicial a su posición estirada? (b) ¿Cuál es la diferencia solo en la energía potencial gravitacional desde su posición de equilibrio inicial hasta su posición estirada? (c) ¿Cuál es la energía cinética del bloque a medida que pasa a través de la posición de equilibrio desde su posición estirada?
Estrategia
En las partes (a) y (b), queremos encontrar una diferencia en la energía potencial, por lo que podemos usar la Ecuación 8.6 y la Ecuación 8.4, respectivamente. Cada una de estas expresiones toma en consideración el cambio en la energía en relación con otra posición, enfatizando aún más que la energía potencial se calcula con una referencia o un segundo punto. Al elegir las convenciones del punto más bajo en el diagrama donde la energía potencial gravitacional es cero y la posición de equilibrio del resorte donde la energía potencial elástica es cero, estas diferencias en las energías ahora se pueden calcular. En la parte (c), echamos un vistazo a las diferencias entre las dos energías potenciales. La diferencia entre los dos resultados en energía cinética, ya que no hay fricción o arrastre en este sistema que puede tomar energía del sistema.
Solución
Dado que la energía potencial gravitacional es cero en el punto más bajo, el cambio en la energía potencial gravitacional es
La posición de equilibrio del resorte se define como energía potencial cero. Por lo tanto, el cambio en la energía potencial elástica es
$$\Delta U_{elástica} = 0 - \frac12 ky_{pull}^2 = - \Big(\frac12\Big)(6.0Nm) (5.0cm)^2 = -0.75 J$$El bloque comenzó a tirar hacia abajo con una energía potencial relativa de $0.75J$. La energía potencial gravitatoria requerida para elevarse a $5.0cm$ es $0.60J$. La energía que permanece en esta posición de equilibrio debe ser energía cinética. Podemos resolver esta ganancia en energía cinética de la Ecuación 8.2,
$$\Delta K = - (\Delta U_{elástica} + \Delta U_{grav}) = - (- 0.75 J + 0.60 J) = 0.15 J$$Explicación
Aunque las energías potenciales son relativas a una ubicación cero elegida, las soluciones a este problema serían las mismas si los puntos de energía cero se eligieran en diferentes ubicaciones.
 Comprueba tu aprendizaje 8.4
Comprueba tu aprendizaje 8.4
¡Observa esta simulación para que aprendas sobre la conservación de la energía con un patinador! Construye pistas, rampas y saltos para el patinador y observa la energía cinética, la energía potencial y la fricción mientras se mueve. ¡También puedes llevar al patinador a diferentes planetas o incluso al espacio!
En la Tabla 8.2 se muestra una una variedad de energías para darte una idea sobre los valores de energía típicos asociados con ciertos eventos. Algunos de éstos se calculan usando energía cinética, mientras que otros se calculan usando cantidades encontradas en una forma de energía potencial que puede no haber sido discutida hasta este punto.
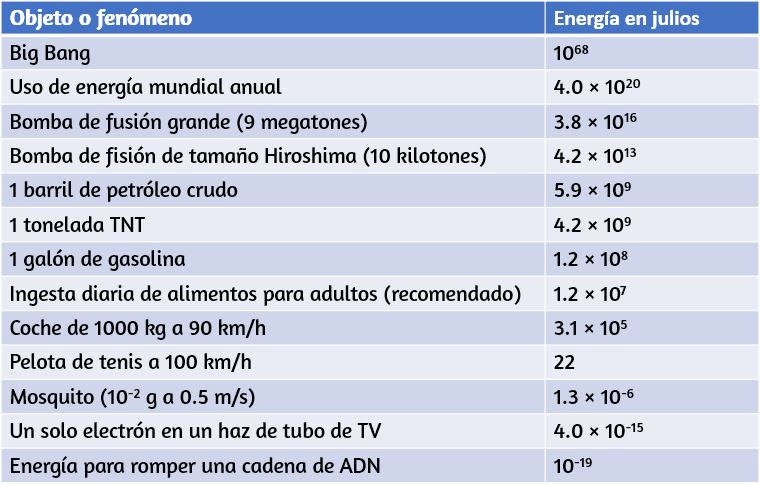
Fuerzas conservadoras y no conservadoras
En lo que hemos visto, cualquier transición entre energía cinética y potencial conserva la energía total del sistema. Esto era independiente de la ruta o trayectoria, lo que significa que podemos comenzar y detenernos en cualquier punto del problema, y la energía total del sistema -potencial, cinética, etc.- en estos puntos es igual el uno al otro. Esto es característico de una fuerza conservadora. Tratamos con las fuerzas conservadoras en la sección anterior, como la fuerza de la gravedad y la fuerza de un resorte. Al comparar el movimiento del balón de fútbol en la Figura 8.2, la energía total del sistema nunca cambia, a pesar de que la energía potencial gravitacional del fútbol aumenta, a medida que la pelota sube respecto al suelo y vuelve a la energía potencial gravitacional inicial cuando el receptor atrapa la pelota.
Las fuerzas no conservativas son fuerzas disipativas como la fricción o la resistencia del aire. Estas fuerzas alejan la energía del sistema a medida que avanza el sistema, energía que no puede recuperar. Estas fuerzas dependen de la trayectoria; por lo tanto, importa dónde comienza y dónde se detiene el objeto.
El trabajo realizado por una fuerza conservadora es independiente de la trayectoria; en otras palabras, el trabajo realizado por una fuerza conservadora es el mismo para cualquier camino que conecte dos puntos: $$\begin{split} W_{AB, ruta1} &= \int_{AB, ruta1}\bold{\vec{F}}_{cons}\cdot d\bold{\vec{r}}\\ &= W_{AB, ruta2} = \int_{AB, ruta2} \bold{\vec{F}}_{cons}\cdot d\bold{\vec{r}}\tag{8.8} \end{split}$$
En la ecuación 8.9, utilizamos la notación de un círculo en el medio del signo integral para una integral de línea sobre un camino cerrado, una notación encontrada en la mayoría de los textos de física e ingeniería.
La ecuación 8.8 y la ecuación 8.9 son equivalentes porque cualquier camino cerrado es la suma de dos caminos: el primero va de $A$ a $B$, y el segundo va de $B$ a $A$. El trabajo hecho por un camino de $B$ a $A$ es el negativo del trabajo hecho por el mismo camino de $A$ a $B$, donde $A$ y $B$ son dos puntos en el camino cerrado:
$$\begin{split} 0 &= \int \bold{\vec{F}}_{cons}\cdot d\bold{\vec{r}}\\ &= \int_{AB, ruta1}\bold{\vec{F}}_{cons}\cdot d\bold{\vec{r}} + \int_{BA, ruta2}\\ &= \int_{AB, ruta1}\bold{\vec{F}}_{cons}\cdot d\bold{\vec{r}} - \int_{AB, ruta2} \end{split}$$Puedes preguntar cómo hacemos para probar si una fuerza es conservadora o no, ya que las definiciones implican todas y cada una de las rutas desde $A$ hasta $B$, o cualquier ruta cerrada, pero para hacer la integral para el trabajo, debes elegir una camino particular. Una respuesta es que el trabajo realizado es independiente del camino si el trabajo infinitesimal $\bold{\vec{F}}\cdot ;d\bold{\vec{r}}$ es un diferencial exacto, la forma en que el trabajo neto infinitesimal era igual al diferencial exacto de la energía cinética, $dW_{neta} = m\bold{\vec{v}}\cdot d\bold{\vec{v}} = d\frac12 mv^2$, cuando derivamos el teorema de trabajo-energía. Hay condiciones matemáticas que puedes usar para probar si el trabajo infinitesimal realizado por una fuerza es un diferencial exacto, y la fuerza es conservadora. Estas condiciones solo implican diferenciación y, por lo tanto, son relativamente fáciles de aplicar. En dos dimensiones, la condición para que $\bold{\vec{F}}\cdot d\bold{\vec{r}} = F_xdx + F_ydy$ sea una diferencia exacta es
Puedes recordar que el trabajo realizado por la fuerza en el ejemplo 7.4 depende de la ruta. Para esa fuerza, $$F_x = (5 N/m)y\;\;\text{y } F_y = (10 N/m)x$$
Por lo tanto,
$$\Big(\frac{dF_x}{dy}\Big) = 5 N/m \ne \Big(\frac{dF_y}{dx}\Big) = 10 N/m$$lo que indica que es una fuerza no conservadora. ¿Puedes ver lo que podrías cambiar para convertirla en una fuerza conservadora?
Ejemplo 8.5
Conservadora o no?

¿Cuál de las siguientes fuerzas bidimensionales son conservadoras y cuáles no? Supongamos que $a$ y $b$ son constantes con unidades apropiadas:
(a) $axy^3\^{\bold{i}} + ayx^3\^{\bold{j}}$,
(b) $a[(y^2/x)\^{\bold{i}} + 2yln(x/b)\^{\bold{j}}$,
(c) $\frac{ax\^{\bold{i}} + ay\^{\bold{j}}}{x^2 + y^2}$
Estrategia
Aplica la condición indicada en la Ecuación 8.10, es decir, usando las derivadas de los componentes de cada fuerza indicada.
Si la derivada de la componente y de la fuerza con respecto a $x$ es igual a la derivada de la componente x de la fuerza con respecto a $y$, la fuerza es una fuerza conservadora, lo que significa la ruta tomada para la energía potencial o el trabajo los cálculos siempre arrojan los mismos resultados.
Solución
a. $\frac{dF_x}{dy} = \frac{d(axy^3)}{dy} = 3axy^2$ y $\frac{dF_y}{dx} = \frac{d(ayx^3}{dx} = 3ayx^2$, entonces esta fuerza no es conservadora.
b. $\frac{dF_x}{dy} = \frac{2ay}{dy} = \frac{dF_x}{x}$ y $\frac{dF_y}{dx} = \frac{d(2ayln(x/b))}{dx} = \frac{2ay}{x}$, es una fuerza conservativa.
c. $\frac{dF_x}{dy} = \frac{d(ax/(x^2 + y^2)}{dy} = -\frac{ax(2y)}{(x^2 + y^2)^2} = \frac{dF_y}{dx}$, también conservativa.
Explicación
Las condiciones en la Ecuación 8.10 son derivadas de funciones de una sola variable; en tres dimensiones, existen condiciones similares que implican más derivadas.
 Comprueba tu aprendizaje 8.5
Comprueba tu aprendizaje 8.5
Antes de abandonar esta sección, observamos que las fuerzas no conservativas no tienen energía potencial asociada a ellas porque la energía se pierde en el sistema y no pueden convertirse en trabajo útil más adelante. Entonces siempre hay una fuerza conservadora asociada con cada energía potencial. Hemos visto que la energía potencial se define en relación con el trabajo realizado por las fuerzas conservadoras. Esa relación, Ecuación 8.1, involucraba una integral para el trabajo; comenzando con la fuerza y el desplazamiento, se integró para obtener el trabajo y el cambio en la energía potencial. Sin embargo, la integración es la operación inversa de la diferenciación; igualmente podría haber comenzado con la energía potencial y tomar su derivada, con respecto al desplazamiento, para obtener la fuerza. El incremento infinitesimal de energía potencial es el producto punto de la fuerza y el desplazamiento infinitesimal,
$$dU = −\bold{\vec{F}}\cdot d\bold{\vec{l}} = −F_ldl$$Aquí, elegimos representar el desplazamiento en una dirección arbitraria por $d\bold{\vec{l}}$, para no restringirnos a ninguna dirección de coordenadas particular. También expresamos el producto punto en términos de la magnitud del desplazamiento infinitesimal y el componente de la fuerza en su dirección. Ambas cantidades son escalares, por lo que puede dividir por dl para obtener
Esta ecuación proporciona la relación entre la fuerza y la energía potencial asociada con ella. En otras palabras, el componente de una fuerza conservadora, en una dirección particular, es igual al negativo de la derivada de la energía potencial correspondiente, con respecto a un desplazamiento en esa dirección.
Para un movimiento unidimensional, digamos a lo largo del eje $x$, la ecuación 8.11 da la fuerza vectorial completa, $\displaystyle\bold{\vec{F}} = F_x\^{\bold{i}} = -\frac{\partial U}{\partial x\^{\bold{i}}}$.
En dos dimensiones,
$$\bold{\vec{F}} = F_x\^{\bold{i}} + F_y\^{\bold{j}} = -\frac{\partial U}{\partial x}\^{\bold{i}} - \frac{\partial U}{\partial y}\^{\bold{j}}$$A partir de esta ecuación, puedes ver por qué la Ecuación 8.11 es la condición para que el trabajo sea un diferencial exacto, en términos de las derivadas de los componentes de la fuerza. En general, se usa una notación de derivada parcial. Si una función tiene muchas variables, la derivada se toma solo de la variable que especifica la derivada parcial.
Las otras variables se mantienen constantes. En tres dimensiones, agregas otro término para el componente $z$, y el resultado es que la fuerza es el negativo del gradiente de la energía potencial. Sin embargo, no vamos a ver ejemplos tridimensionales por el momento.
Ejemplo 8.6
Fuerza debido a una energía potencial bicuadrática
La energía potencial para una partícula sometida a movimiento unidimensional a lo largo del eje $x$ es
$$U(x) = \frac14 cx^4$$donde $c = 8 N/m^3$. Su energía total en $x = 0$ es $2 J$, y no está sujeta a ninguna fuerza no conservativa. Encuentra (a) las posiciones donde su energía cinética es cero y (b) las fuerzas en esas posiciones.
Estrategia
(a) Podemos encontrar las posiciones donde $K = 0$, por lo que la energía potencial es igual a la energía total del sistema dado. (b) Usando la Ecuación 8.11, podemos encontrar la fuerza evaluada en las posiciones encontradas desde la parte anterior, ya que la energía mecánica se conserva.
Solución
La energía total del sistema de $2 J$ es igual a la energía elástica bicuadrática que se da en el problema,
$$2 J = \frac14 (8 N/m^3)x_f^4$$La solución para $x_f$ da como resultado $x_f = \pm 1m$.
(b) De la ecuación 8.11,
$$F_x = -dU/dx = -cx^3$$Por lo tanto, al evaluar la fuerza a $\pm 1 m$, obtenemos
$$\bold{\vec{F}} = -(8 N/m^3)(\pm 1m) 3\^{\bold{i}} = \pm 8N\^{\bold{i}}$$En ambas posiciones, la magnitud de las fuerzas es $8 N$ y las direcciones son hacia el origen, ya que esta es la energía potencial para una fuerza de restauración.
Explicación
Encontrar la fuerza de la energía potencial es matemáticamente más fácil que encontrar la energía potencial de la fuerza, porque diferenciar una función es generalmente más fácil que integrarla.
 Comprueba tu aprendizaje 8.6
Comprueba tu aprendizaje 8.6
Conservacion de la energia
En esta sección, elaboramos y ampliamos el resultado que derivamos en Energía potencial de un sistema, donde re-escribimos el teorema de trabajo-energía en términos del cambio en las energías cinéticas y potenciales de una partícula. Esto nos llevará a una discusión sobre el importante principio de la conservación de la energía mecánica.
A medida que continúes examinando otros temas en física, en capítulos posteriores de este libro, verás cómo esta ley de conservación se generaliza para abarcar otros tipos de energía y transferencias de energía. La última sección de este capítulo proporciona una vista previa.
Los términos 'cantidad conservada' y 'ley de conservación' tienen significados científicos específicos en física, que son diferentes de los significados cotidianos asociados con el uso de estas palabras (el mismo comentario también es cierto sobre los usos científicos y cotidianos de la palabra "trabajo"). En el uso diario, puedes conservar agua al no usarla, o al usar menos, o al volver a usarla. El agua está compuesta de moléculas formadas por dos átomos de hidrógeno y uno de oxígeno. Junta estos átomos para formar una molécula y creas agua; disocia los átomos en tal molécula y destruyes el agua. Sin embargo, en el uso científico, una cantidad conservada para un sistema permanece constante, cambia en una cantidad definida que se transfiere a otros sistemas y/o se convierte en otras formas de esa cantidad. Una cantidad conservada, en el sentido científico, puede transformarse, pero no crearse o destruirse estrictamente. Por lo tanto, no existe una ley física de conservación del agua.
Sistemas con una sola partícula u objeto
Primero consideramos un sistema con una sola partícula u objeto. Volviendo a nuestro desarrollo de la Ecuación 8.2, recordemos que primero separamos todas las fuerzas que actúan sobre una partícula en tipos conservadores y no conservadores, y escribimos el trabajo hecho por cada tipo de fuerza como un término separado en el teorema del trabajo-energía. Luego reemplazamos el trabajo realizado por las fuerzas conservadoras por el cambio en la energía potencial de la partícula, combinándola con el cambio en la energía cinética de la partícula para obtener la Ecuación 8.2.
Ahora, escribimos esta ecuación sin el paso intermedio y definimos la suma de las energías cinéticas y potenciales, $K + U = E$ como la energía mecánica de la partícula.
La energía mecánica $E$ de una partícula permanece constante a menos que fuerzas externas al sistema o fuerzas no conservativas trabajen en ella, en cuyo caso, el cambio en la energía mecánica es igual al trabajo realizado por las fuerzas no conservativas: $$W_{nc, AB} = \delta (K + U)_{AB} = \Delta E_{AB}\tag{8.12}$$
Esta declaración expresa el concepto de conservación de energía para una partícula clásica siempre que no haya un trabajo no conservador. Recuerde que una partícula clásica es solo una masa puntual, no relativista y obedece a las leyes del movimiento de Newton. En la Relatividad, veremos que la conservación de la energía todavía se aplica a una partícula no clásica, pero para que eso suceda, debemos hacer un ligero ajuste a la definición de energía.
A veces es conveniente separar el caso donde el trabajo realizado por fuerzas no conservativas es cero, ya sea porque no se asume que tales fuerzas estén presentes o, como la fuerza normal, no funcionan cuando el movimiento es paralelo a la superficie. Entonces
En este caso, la conservación de la energía mecánica se puede expresar de la siguiente manera: la energía mecánica de una partícula no cambia si no funcionan las fuerzas no conservativas que pueden actuar sobre ella.
Comprender el concepto de conservación de la energía es lo importante, no la ecuación particular que utilizas para expresarlo.
1. Identifica el cuerpo o los cuerpos que se estudiarán (el sistema). A menudo, en las aplicaciones del principio de conservación de la energía mecánica, estudiamos más de un cuerpo al mismo tiempo.
2. Identifica todas las fuerzas que actúan sobre el cuerpo o los cuerpos.
3. Determina si cada fuerza que funciona es conservadora. Si una fuerza no conservativa (por ejemplo, la fricción) está haciendo un trabajo, entonces la energía mecánica no se conserva. El sistema debe entonces analizarse con trabajo no conservador, Ecuación 8.13.
4. Para cada fuerza que funciona, elije un punto de referencia y determina la función de energía potencial para la fuerza. Los puntos de referencia para las diversas energías potenciales no tienen que estar en la misma ubicación.
5. Aplica el principio de la conservación de la energía mecánica estableciendo la suma de las energías cinéticas y las energías potenciales iguales en cada punto de interés.
Ejemplo 8.7
Péndulo simple
Una partícula de masa $m$ se cuelga del techo mediante una cuerda sin masa de $1,0 m $de longitud, como se muestra en la Figura 8.7. La partícula se libera del reposo, cuando el ángulo entre la cuerda y la dirección vertical hacia abajo es de $30\degree$. ¿Cuál es su velocidad cuando alcanza el punto más bajo de su arco?
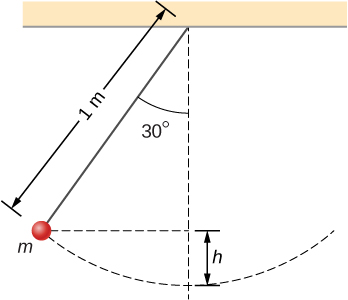
Estrategia
Usando nuestra estrategia de resolución de problemas, el primer paso es definir que estamos interesados en el sistema de partículas de la Tierra. En segundo lugar, solo la fuerza gravitacional está actuando sobre la partícula, que es conservadora (paso 3).
Despreciamos la resistencia del aire en el problema y no se realiza ningún trabajo mediante la tensión de la cuerda, que es perpendicular al arco del movimiento. Por lo tanto, la energía mecánica del sistema se conserva, como se representa mediante la ecuación 8.13, $0 = \Delta(K + U)$. Debido a que la partícula comienza desde el reposo, el aumento en la energía cinética es justo la energía cinética en el punto más bajo. Este aumento en la energía cinética es igual a la disminución en la energía potencial gravitacional, que podemos calcular a partir de la geometría. En el paso 4, elegimos un punto de referencia para que la energía potencial gravitacional cero esté en el punto vertical más bajo que alcanza la partícula, que es la oscilación media. Por último, en el paso 5, establecemos la suma de las energías en el punto más alto (inicial) del balanceo hasta el punto más bajo (final) del balanceo para finalmente hallar la velocidad final.
Solución
Estamos despreciando las fuerzas no conservativas, por lo que escribimos la fórmula de conservación de energía relacionando la partícula en el punto más alto (inicial) y el punto más bajo en el columpio (final) como
$$K_i + U_i = K_f + U_f$$Como la partícula se libera del reposo, la energía cinética inicial es cero. En el punto más bajo, definimos que la energía potencial gravitacional es cero. Por lo tanto, nuestra fórmula de conservación de la energía se reduce a
$$0 + mgh = \frac12 mv^2$$ $$v =\sqrt{2gh}$$La altura vertical de la partícula no se da directamente en el problema. Esto se puede resolver usando la trigonometría y dos datos: la longitud del péndulo y el ángulo a través del cual la partícula se levanta verticalmente. Mirando el diagrama, la línea punteada vertical es la longitud de la cuerda del péndulo. La altura vertical está etiquetada como h. La otra longitud parcial de la cuerda vertical se puede calcular con trigonometría. Esa pieza se resuelve por
$$cos\theta = x/L, x = Lcos\theta$$Por lo tanto, mirando las dos partes de la cuerda, podemos hallar la altura $h$,
$$x + h = L\\ Lcos\theta + h = L\\ h = L − Lcos\theta = L(1 − cos\theta )$$Sustituimos esta altura en la expresión anterior, permitiendo calcular la velocidad.
$$\begin{split} v &= \sqrt{2gL(1 − cos\theta)}\\ &= \sqrt{2(9.8 m/s^2)(1 m)(1 - cos30\degree)}\\ &= 1.62 m/s \end{split}$$Explicación
Encontramos la velocidad directamente desde la conservación de energía mecánica, sin tener que resolver la ecuación diferencial para el movimiento de un péndulo. Podemos abordar este problema en términos de gráficos de barras de la energía total. Inicialmente, la partícula tiene toda la energía potencial, estando en el punto más alto y sin energía cinética.
Cuando la partícula cruza el punto más bajo en la parte inferior del columpio, la energía se mueve desde la columna de energía potencial a la columna de energía cinética.
Por lo tanto, podemos imaginar una progresión de esta transferencia a medida que la partícula se mueve entre su punto más alto, al punto más bajo del columpio y de regreso al punto más alto (Figura 8.8). A medida que la partícula se desplaza desde el punto más bajo en el columpio hasta el punto más alto en el extremo derecho del diagrama, las barras de energía van en el orden inverso de (c) a (b) a (a).
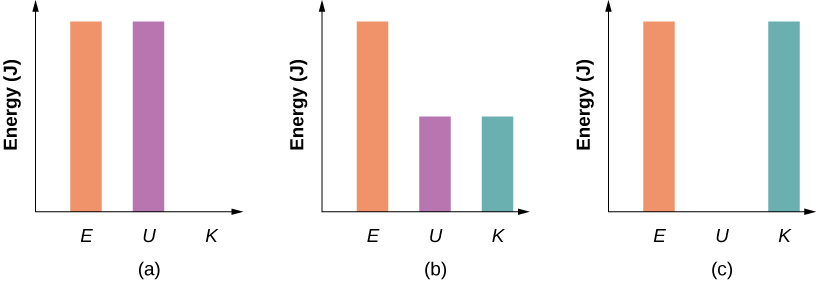
En el siguiente objeto interactivo, diseñado por Anne J Cox (Modelo de energía del péndulo), puedes observar los gráficos de barras que muestran la energía cinética ($EC$) de la marioneta, la energía potencial ($EP$) y la energía mecánica total ($E$). Puedes cambiar la posición inicial de la marioneta (dentro de lo razonable).
Pausa la simulación. Registra la altura, la velocidad y las energías cinética y potencial y encuentra la masa de la marioneta.
 Comprueba tu aprendizaje 8.7
Comprueba tu aprendizaje 8.7
Ejemplo 8.8
Resistencia al aire en un objeto que cae
Un helicóptero flota a una altitud de $1 km$ cuando un panel de su parte inferior se desprende y cae al suelo (Figura 8.9).
La masa del panel es de $15 kg$ y toca el suelo con una velocidad de $45 m/s$. ¿Cuánta energía mecánica se disipó por la resistencia del aire durante el descenso del panel?
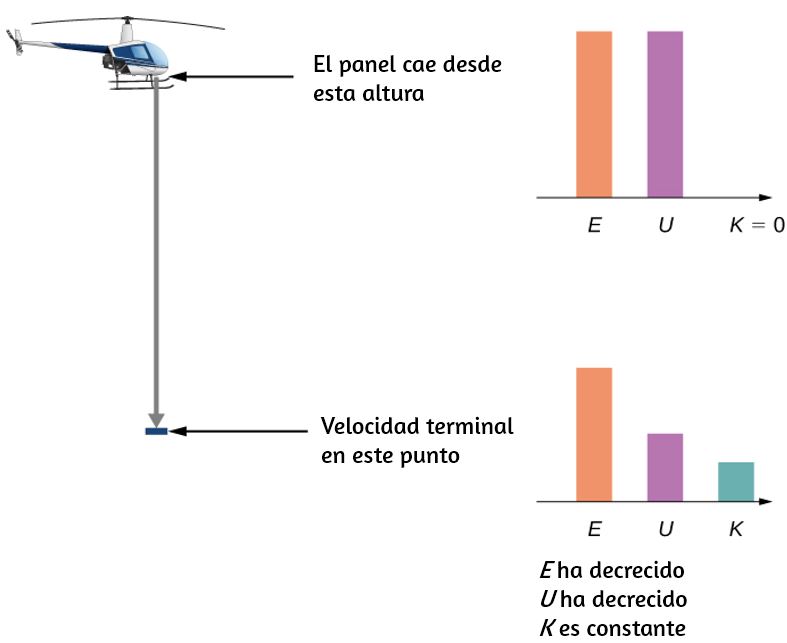
Estrategia
Paso 1: Aquí solo se está investigando un cuerpo.
Paso 2: la fuerza gravitatoria está actuando en el panel, así como la resistencia del aire, que se establece en el problema.
Paso 3: la fuerza gravitatoria es conservadora; sin embargo, la fuerza no conservativa de la resistencia del aire hace un trabajo negativo en el panel descendente, por lo que podemos usar la conservación de energía mecánica, en la forma expresada por la Ecuación 8.12, para encontrar la energía disipada. Esta energía es la magnitud del trabajo:
$$\Delta E_{dis} = |W_{nc, if}| = |\delta (K + U)_{if}|$$Paso 4: la energía cinética inicial, en $y_i = 1 km$, es cero. Establecemos la energía potencial gravitacional en cero a nivel del suelo por conveniencia.
Paso 5: El trabajo no conservador se establece igual a las energías para resolver el trabajo disipado por la resistencia del aire.
Solución
La energía mecánica disipada por la resistencia del aire es la suma algebraica de la ganancia en la energía cinética y la pérdida de energía potencial. Por lo tanto, el cálculo de esta energía es
$$\Delta E_{dis} = |K_f - K_i + U_f - U_i|$$ $$\begin{split} \Delta E_{dis} &= \Big|\frac12 (15 kg)(45 m/s)^2 - 0 + 0 - (15 kg)(9.8 m/s^2)(1000 m)\Big|\\ &= 130 kJ \end{split}$$Explicación
La mayor parte de la energía mecánica inicial del panel ($U_i$), $147 kJ$, se perdió por la resistencia del aire. Ten en cuenta que pudimos calcular la energía disipada sin saber cuál era la fuerza de la resistencia del aire, solo que era disipativa.
 Comprueba tu aprendizaje 8.8
Comprueba tu aprendizaje 8.8
En estos ejemplos, pudimos usar la conservación de la energía para calcular la velocidad de una partícula solo en puntos particulares de su movimiento. Pero el método de analizar el movimiento de partículas, comenzando desde la conservación de energía, es más poderoso que eso. Los tratamientos más avanzados de la teoría de la mecánica te permiten calcular la dependencia del tiempo en el movimiento de una partícula, para una energía potencial dada.
De hecho, a menudo ocurre que la forma de sus energías cinética y potencial proporciona un modelo mejor para el movimiento de partículas, en lugar de una ecuación para la fuerza que actúa sobre él (esto es especialmente cierto para la descripción mecánica cuántica de partículas como electrones o átomos).
Podemos ilustrar algunas de las características más simples de este enfoque basado en la energía considerando una partícula en movimiento unidimensional, con energía potencial $U(x)$ y ninguna interacción no conservativa presente. La ecuación 8.12 y la definición de velocidad requieren
$$K = \frac12 mv^2 = E − U(x)$$Separa las variables $x$ y $t$ e integra, desde un tiempo inicial $t = 0$ a un tiempo arbitrario, para obtener
$$t = \int_0^t dt = \int_{x_0}^x \frac{dt}{\sqrt{2(E − U(x))/m}}$$puedes desarrollar la integral en la Ecuación 8.14, luego resuelves para $x$ como una función de $t$.
Ejemplo 8.9
Aceleración constante
Usa la energía potencial $U(x) = - E(x/x_0)$, para $E \gt 0$, en la Ecuación 8.14 para encontrar la posición $x$ de una partícula en función del tiempo $t$.
Estrategia
Como sabemos cómo cambia la energía potencial en función de $x$, podemos sustituir a $U(x)$ en la ecuación 8.14, integrar y luego resolver para $x$. Esto da como resultado una expresión de $x$ como una función del tiempo con constantes de energía $E$, masa $m$ y la posición inicial $x_0$.
Solución
Siguiendo los primeros dos pasos sugeridos en la estrategia anterior,
Resolviendo para la posición, obtenemos $x(t) = x_0 - \frac12 (E/mx_0)t^2$.
Explicación
La posición en función del tiempo, para este potencial, representa un movimiento unidimensional con aceleración constante, $a = (E/mx_0)$, comenzando en reposo desde la posición $x_0$. Esto no es tan sorprendente, ya que esta es una energía potencial para una fuerza constante, $F = -dU/dx = E/x_0$, y $a = F \;m$.
 Comprueba tu aprendizaje 8.9
Comprueba tu aprendizaje 8.9
Veremos otro ejemplo más apropiado físicamente del uso de la ecuación 8.13 después de haber explorado algunas implicaciones adicionales que pueden extraerse de la forma funcional de la energía potencial de una partícula.
Sistemas con varias partículas u objetos
Los sistemas generalmente consisten en más de una partícula u objetos. Sin embargo, la conservación de la energía mecánica, en una de las formas de la Ecuación 8.12 o la Ecuación 8.13, es una ley fundamental de la física y se aplica a cualquier sistema. Solo debes incluir las energías cinéticas y potenciales de todas las partículas y el trabajo realizado por todas las fuerzas no conservadoras que actúan sobre ellas.
Hasta que aprendas más acerca de la dinámica de los sistemas compuestos de muchas partículas, en momento lineal y colisiones, rotación de eje fijo y momento angular, es mejor posponer la discusión sobre la aplicación de la conservación de energía hasta ese momento.
Diagramas de energía potencial y estabilidad
A menudo, puedes obtener una gran cantidad de información útil sobre el comportamiento dinámico de un sistema mecánico, simplemente interpretando un gráfico de su energía potencial en función de la posición, llamado diagrama de energía potencial. Esto se logra más fácilmente para un sistema unidimensional, cuya energía potencial se puede trazar en un gráfico de dos dimensiones, por ejemplo, $U(x)$ versus $x$, en una hoja de papel o un programa de computadora. Para sistemas cuyo movimiento está en más de una dimensión, el movimiento debe estudiarse en un espacio tridimensional. Simplificaremos nuestro procedimiento solo para movimiento unidimensional.
Primero, veamos un objeto, que cae verticalmente, cerca de la superficie de la Tierra, en ausencia de resistencia al aire.
La energía mecánica del objeto se conserva, $E = K + U$, y la energía potencial, con respecto a cero en el nivel del suelo, es $U(y) = mgy$, que es una línea recta a través del origen con pendiente mg. En el gráfico que se muestra en la Figura 8.10, el eje $x$ es la altura sobre el suelo y el eje $y$ es la energía del objeto.
La línea en la energía $E$ representa la energía mecánica constante del objeto, mientras que las energías cinéticas y potenciales, $K_A$ y $U_A$, se indican a una altura particular $y_A$. Puedes ver cómo la energía total se divide entre la energía cinética y potencial a medida que cambia la altura del objeto.
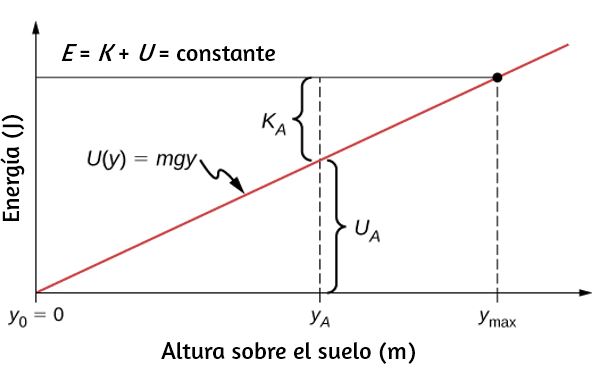
Como la energía cinética nunca puede ser negativa, existe una energía potencial máxima y una altura máxima, que un objeto con la energía total dada no puede exceder:
Si usamos el punto de referencia de energía potencial gravitacional de cero en $y_0$, podemos reescribir la energía potencial gravitacional $U$ como $mgy$. Resolviendo para y obtenemos
$$y \le E/mg = y_{max}$$Notamos en esta expresión que la cantidad de energía total dividida por el peso ($mg$) se encuentra a la altura máxima de la partícula, o $y_{max}$. A la altura máxima, la energía cinética y la velocidad son cero, por lo que si el objeto estuviera inicialmente viajando hacia arriba, su velocidad pasaría a cero allí, y $y_{max}$ sería un punto de inflexión en el movimiento. A nivel del suelo, $y_0 = 0$, la energía potencial es cero, y la energía cinética y la velocidad son máximas:
$$U_0 = 0 = E - K_0\\ E = K_0 = \frac12 m_0^2\\ v_0 = \pm\sqrt{2E/m}$$La velocidad máxima $\pm v_0$ da la velocidad inicial necesaria para alcanzar $y_{max}$, la altura máxima, y $-v_0$ representan la velocidad final, después de caer desde $y_{max}$. Puedes leer toda esta información, y más, del diagrama de energía potencial que hemos mostrado.
Considera un sistema resorte-masa en una superficie horizontal, en reposo y sin fricción, de modo que la gravedad y la fuerza de contacto normal no funcionen y puedan ignorarse (Figura 8.11).
Esto es como un sistema unidimensional, cuya energía mecánica E es una constante y cuya energía potencial, con respecto a la energía cero, en el desplazamiento cero, desde la longitud no estirada del resorte $x = 0$, es $$U(x) = \frac12 kx^2$$
Puedes leer el mismo tipo de información del diagrama de energía potencial en este caso, como en el caso del cuerpo en caída libre vertical,
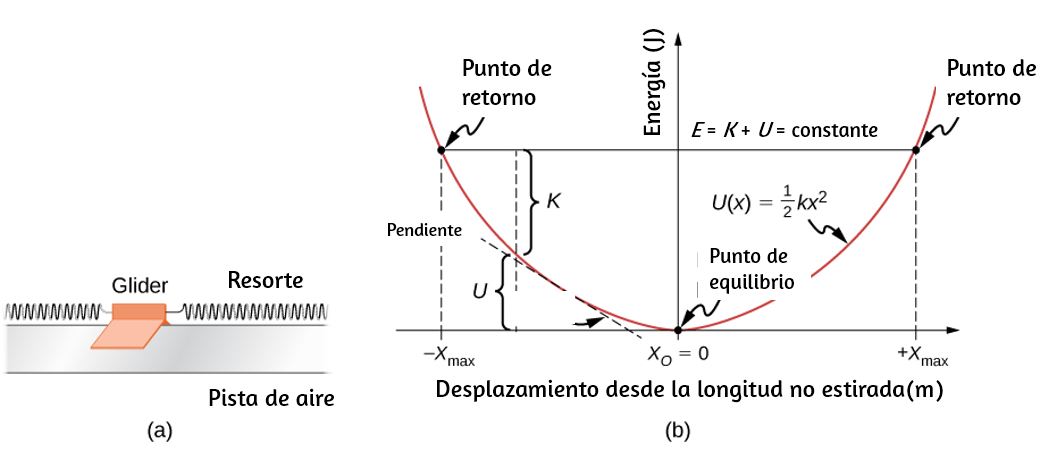
pero dado que la energía potencial del resorte describe una fuerza variable, puedes aprender más de este gráfico. En cuanto al objeto en caída libre vertical, puedes deducir el rango de movimiento permitido físicamente y los valores máximos de distancia y velocidad, desde los límites de la energía cinética, $0 \le K \le E$.
Por lo tanto, $K = 0$ y $U = E$ en un punto de inflexión, de los cuales hay dos para la energía potencial del resorte elástico,
$$x_{max} = \pm \sqrt{2E/k}$$El movimiento del parapente se limita a la región entre los puntos de inflexión, $-x_{max} \le x \le x_{max}$. Esto es cierto para cualquier valor (positivo) de $E$ porque la energía potencial no tiene límites con respecto a $x$.
Por esta razón, además de la forma de la curva de energía potencial, $U(x)$ recibe el nombre de fuente potencial infinita. En la parte inferior de la fuente potencial, $x = 0, U = 0$ y la energía cinética es un máximo, $K = E$, entonce $v_{max} = \pm \sqrt{2E/m}$.
Sin embargo, desde la pendiente de esta curva de energía potencial, también puedes deducir información sobre la fuerza sobre el parapente y su aceleración. Vimos anteriormente que el negativo de la pendiente de la energía potencial es la fuerza del resorte, que en este caso también es la fuerza neta, y por lo tanto es proporcional a la aceleración. Cuando $x = 0$, la pendiente, la fuerza y la aceleración son todas cero, por lo que este es un punto de equilibrio. El negativo de la pendiente, en cualquier lado del punto de equilibrio, da una fuerza que apunta hacia atrás al punto de equilibrio, $F = \pm kx$, por lo que el equilibrio se denomina estable y la fuerza se llama fuerza de restauración. Esto implica que $U(x)$ tiene un mínimo relativo allí. Si la fuerza en cualquier lado de un punto de equilibrio tiene una dirección opuesta a esa dirección de cambio de posición, el equilibrio se denomina inestable, y esto implica que $U(x)$ tiene un máximo relativo allí.
Ejemplo 8.10
Diagrama de energía potencial cuártica y cuadrática
La energía potencial para una partícula sometida a movimiento unidimensional a lo largo del eje $x$ es $U(x) = 2(x^4 - x^2)$, donde $U$ está en joules y $x$ está en metros. La partícula no está sujeta a ninguna fuerza no conservativa y su energía mecánica es constante en $E = -0.25J$. (a) ¿El movimiento de la partícula está limitado a cualquier región en el eje x, y si es así, cuáles son? (b) ¿Hay algún punto de equilibrio? De ser así, ¿dónde están y son estables o inestables?
Estrategia
Primero, necesitamos graficar la energía potencial como una función de $x$. La función es cero en el origen, se vuelve negativa a medida que x aumenta en las direcciones positiva o negativa ($x^2$ es mayor que $x^4$ para $x \lt 1$), y luego se vuelve positiva en $|x|$ suficientemente grande. La gráfica debe verse como un doble pozo potencial, con los ceros determinados al resolver la ecuación $U(x) = 0$, y los extremos determinados examinando la primera y segunda derivadas de $U(x)$, como se muestra en la Figura 8.12
Puedes encontrar los valores de (a) las regiones permitidas a lo largo del eje $x$, para el valor dado de la energía mecánica, a partir de la condición de que la energía cinética no puede ser negativa, y (b) los puntos de equilibrio y su estabilidad de las propiedades de la fuerza (estable para un mínimo relativo e inestable para un máximo relativo de energía potencial).
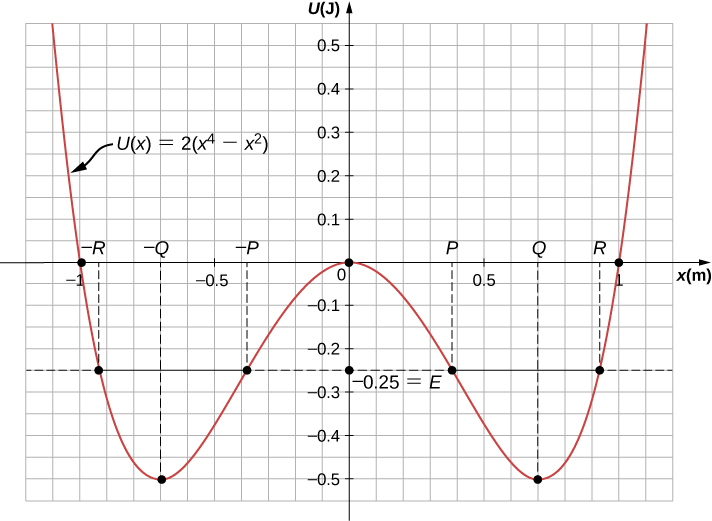
Puedes simplemente observar el gráfico para obtener respuestas cualitativas a las preguntas de este ejemplo. Eso, después de todo, es el valor de los diagramas de energía potenciales. Puedes ver que hay dos regiones permitidas para el movimiento ($E \gt U$) y tres puntos de equilibrio (pendiente $dU/dx = 0$), de los cuales el central es inestable ($d^2U/dx^2 \lt 0$), y los otros dos son estable ($d^2U/dx^2 \gt 0$).
Solución
a. Para encontrar las regiones permitidas para $x$, usamos la condición
Si completamos el cuadrado en $x^2$, esta condición se simplifica a $2\Big(x^2 -\frac12\Big)^2\le \frac14$, que podemos resolver para obtener
$$\frac12 - \sqrt{\frac18} \le x^2 \le \frac12 + \sqrt{\frac18}1/8$$Esto representa dos regiones permitidas, $x_p \le x \le x_R$ y $-x_R \le x \le -x_p$, donde $x_p = 0.38$ y $x_R = 0.92$ (en metros).
b. Para encontrar los puntos de equilibrio, resolvemos la ecuación
$$dU/dx = 8x^3 - 4x = 0$$y encontramos $x = 0$ y $x = \pm x_Q$, donde $x_Q = \frac{1}{\sqrt{2}} = 0.707$ (metros). La segunda derivada
$$d^2U/dx^2 = 24x^2 - 4$$es negativa en $x = 0$, por lo que esa posición es un máximo relativo y el equilibrio allí es inestable. La segunda derivada es positiva en $x = \pm x_Q$, por lo que estas posiciones son mínimas relativas y representan equilibrios estables.
Explicación
La partícula en este ejemplo puede oscilar en la región permitida sobre cualquiera de los dos puntos de equilibrio estables que encontramos, pero no tiene suficiente energía para escapar de cualquier potencial en el que se encuentre inicialmente.
La conservación de la energía mecánica y las relaciones entre la energía cinética y la velocidad, y la energía y fuerza potenciales, te permiten deducir mucha información sobre el comportamiento cualitativo del movimiento de una partícula, así como también cierta información cuantitativa, a partir de un gráfico de su energía potencial.
 Comprueba tu aprendizaje 8.10
Comprueba tu aprendizaje 8.10
Ejemplo 8.11
Oscilaciones sinusoidales
Encuentra $x(t)$ para una partícula que se mueve con una energía mecánica constante $E \gt 0$ y una energía potencial $U(x) = \frac12 kx^2$, cuando la partícula comienza desde el reposo en el tiempo $t = 0$.
Estrategia
Seguimos los mismos pasos que en el ejemplo 8.9. Sustituye la energía potencial U por la ecuación 8.14 y resta las constantes, como $m$ o $k$. Integra la función y resuelve la expresión resultante para la posición, que ahora es una función del tiempo.
$$\begin{split} t &= \int_{x_0}^x \frac{dx}{\sqrt{(k/m)[(2E/k) - x^2]}}\\ &= \sqrt{\frac{m}{k}}\bigg[sen^{-1}\Big(\frac{x}{\sqrt{2E/k}}\Big) - sen^{-1} \Big(\frac{x_0}{\sqrt{2E/k}}\Big)\bigg] \end{split}$$A partir de las condiciones iniciales en $t = 0$, la energía cinética inicial es cero y la energía potencial inicial es $\frac12 kx_0^2 = E$, desde donde se puede ver que $x_0/\sqrt{(2E / k)} = \pm 1$ y $sen^{-1}(\pm 1) = \pm 90\degree$. Ahora puedes resolver x:
$$\begin{split} x(t) &= \sqrt{2E/k} sen \Big[\big(\sqrt{k/m}\big)t \pm 90\degree \Big]\\ &= \pm \sqrt{2E/k} cos\Big [\big(\sqrt{k/m}\big)t\Big] \end{split}$$Explicación
Unos pocos párrafos antes, nos referimos a este sistema de masa-resorte como un ejemplo de un oscilador armónico. Aquí, anticipamos que un oscilador armónico ejecuta oscilaciones sinusoidales con un desplazamiento máximo de $\sqrt{(2E/k)}$ (llamado amplitud) y una tasa de oscilación de $(1/2\pi)\sqrt{k/m}$ (llamada la frecuencia).
 Comprueba tu aprendizaje 8.11
Comprueba tu aprendizaje 8.11
Fuentes de energía
En este capítulo, hemos estudiado la energía. Aprendimos que la energía puede tomar diferentes formas y puede transferirse de una forma a otra. Encontrarás que la energía se discute en muchos contextos cotidianos, así como científicos, porque está involucrada en todos los procesos físicos.
También será evidente que muchas situaciones se entienden mejor, o se conceptualizan más fácilmente, al considerar la energía. Hasta el momento, ningún resultado experimental ha contradicho la conservación de la energía. De hecho, cada vez que las medidas parecen estar en conflicto con la conservación de energía, se han descubierto o reconocido nuevas formas de energía de acuerdo con este principio.
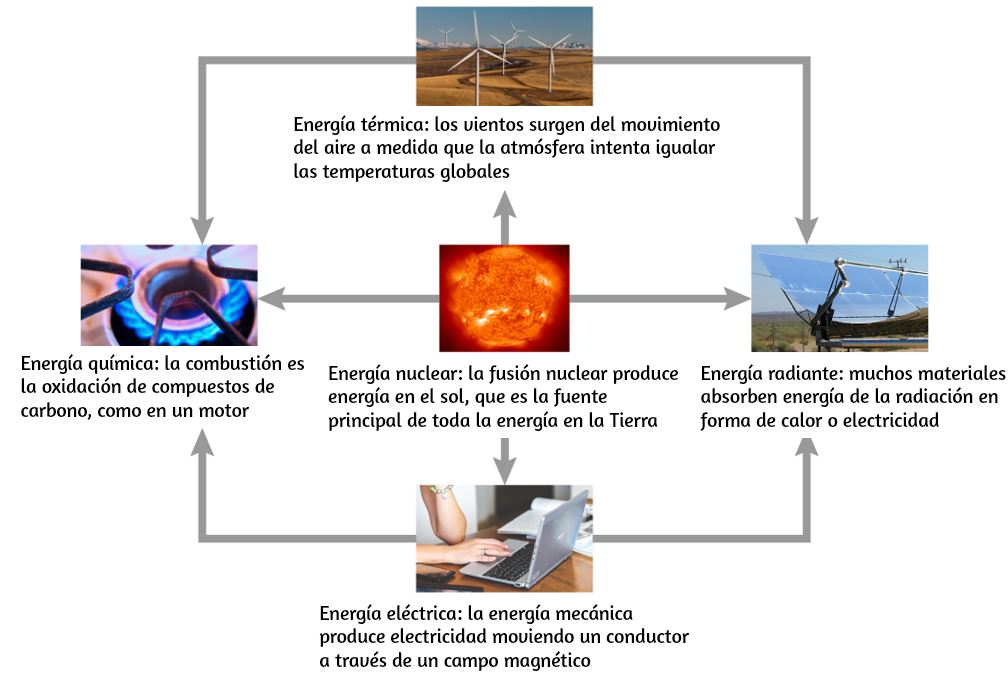
¿Cuáles son algunas otras formas de energía? Muchas de éstas serán cubiertas en capítulos posteriores (también observa la Figura 8.13), pero detallemos algunas aquí:
- Los átomos y moléculas dentro de todos los objetos están en movimiento aleatorio. La energía cinética interna de estos movimientos aleatorios se llama energía térmica, porque está relacionada con la temperatura del objeto. Ten en cuenta que la energía térmica también puede ser transferida de un lugar a otro, no transformada o convertida, por los procesos familiares de conducción, convección y radiación. En este caso, la energía se conoce como energía térmica.
- La energía eléctrica es una forma común que se convierte en muchas otras formas y funciona en una amplia gama de situaciones prácticas.
- Los combustibles, como la gasolina y los alimentos, tienen energía química, que es energía potencial que surge de su estructura molecular. La energía química se puede convertir en energía térmica por reacciones como la oxidación. Las reacciones químicas también pueden producir energía eléctrica, como en las baterías. La energía eléctrica puede, a su vez, producir energía térmica y luz, como en un calentador eléctrico o una bombilla de luz.
- La luz es solo un tipo de radiación electromagnética o energía radiante, que también incluye radio, infrarrojo, ultravioleta, rayos X y rayos gamma. Todos los cuerpos con energía térmica pueden irradiar energía en ondas electromagnéticas.
- La energía nuclear proviene de reacciones y procesos que convierten cantidades medibles de masa en energía. La energía nuclear se transforma en energía radiante en el Sol, en energía térmica en las calderas de las centrales nucleares y luego en energía eléctrica en los generadores de las centrales eléctricas. Estas y todas las otras formas de energía pueden transformarse entre sí y, hasta cierto punto, pueden convertirse en trabajo mecánico.
La transformación de la energía de una forma a otra ocurre todo el tiempo. La energía química en los alimentos se convierte en energía térmica a través del metabolismo; la energía de la luz se convierte en energía química a través de la fotosíntesis. Otro ejemplo de conversión de energía ocurre en una célula solar.
La luz solar que incide en una célula solar produce electricidad, que puede usarse para hacer funcionar motores eléctricos o calentar agua. En un ejemplo que abarca muchos pasos, la energía química contenida en el carbón se convierte en energía térmica, ya que se quema en un horno, para transformar el agua en vapor, en una caldera.
Parte de la energía térmica del vapor se convierte luego en energía mecánica a medida que se expande y hace girar una turbina, que está conectada a un generador para producir energía eléctrica. En estos ejemplos, no toda la energía inicial se convierte en las formas mencionadas, porque parte de la energía siempre se transfiere al entorno.
La energía es un elemento importante en todos los niveles de la sociedad. Vivimos en un mundo muy interdependiente, y el acceso a recursos energéticos adecuados y confiables es crucial para el crecimiento económico y para mantener la calidad de nuestras vidas. Los principales recursos energéticos utilizados en el mundo se muestran en la Figura 8.14.
La figura distingue entre dos tipos principales de fuentes de energía: renovables y no renovables, y además divide cada tipo en unos pocos tipos más específicos. Las fuentes renovables son fuentes de energía que se reponen a través de procesos continuos que se producen de manera natural, en una escala de tiempo que es mucho más corta que la vida anticipada de la civilización que usa la fuente. Las fuentes no renovables se agotan una vez que parte de la energía que contienen se extrae y se convierte en otros tipos de energía.
Los procesos naturales mediante los cuales se forman las fuentes no renovables generalmente se llevan a cabo a lo largo de escalas de tiempo geológicas.
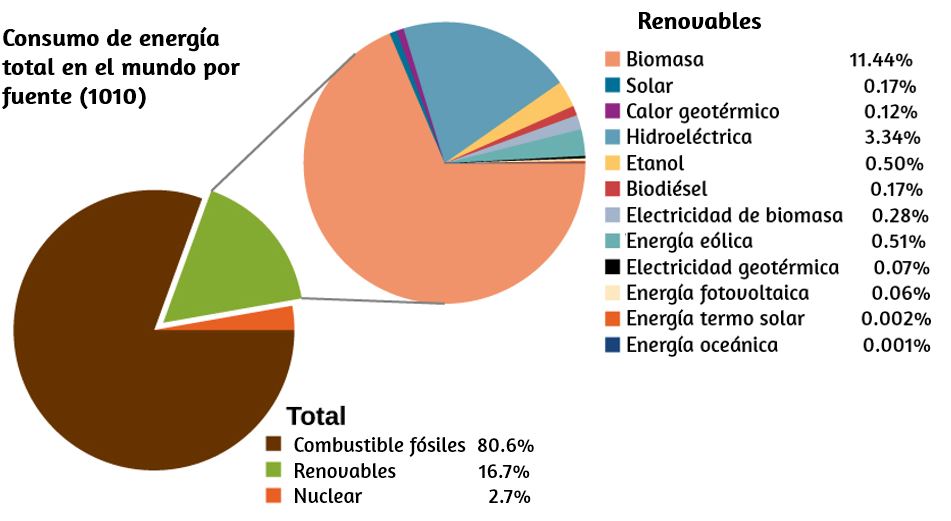
Nuestras fuentes de energía no renovables más importantes son los combustibles fósiles, como el carbón, el petróleo y el gas natural. Estos representan alrededor del 81% del consumo de energía del mundo, como se muestra en la figura. La quema de combustibles fósiles crea reacciones químicas que transforman la energía potencial, en las estructuras moleculares de los reactivos, en energía térmica y productos. Esta energía térmica puede usarse para calentar edificios o para operar maquinaria impulsada por vapor. La combustión interna y los motores a reacción convierten parte de la energía de los gases en rápida expansión, liberados de la gasolina en llamas, en trabajo mecánico.
La generación de energía eléctrica se deriva principalmente de la transferencia de energía en la expansión de vapor, a través de turbinas, al trabajo mecánico, que rota las bobinas de alambre en los campos magnéticos para generar electricidad. La energía nuclear es la otra fuente no renovable que se muestra en la Figura 8.14 y suministra aproximadamente el $3\%$ del consumo mundial. Las reacciones nucleares liberan energía al transformar la energía potencial, en la estructura de los núcleos, en energía térmica, análoga a la liberación de energía en las reacciones químicas. La energía térmica obtenida a partir de las reacciones nucleares puede transferirse y convertirse en otras formas de la misma manera que se utiliza la energía de los combustibles fósiles.
Cuatro de las fuentes de energía renovables enumeradas en la Figura 8.14: las que utilizan material de las plantas como combustible (calor de biomasa, etanol, biodiesel y electricidad de biomasa) implican los mismos tipos de transformaciones y conversiones de energía que se han discutido para los combustibles fósiles y nucleares. Los otros tipos principales de fuentes de energía renovables son la energía hidráulica, eólica, geotérmica y solar.
Un desafortunado subproducto de depender de la energía producida por la combustión de combustibles fósiles es la liberación de dióxido de carbono en la atmósfera y su contribución al calentamiento global. La energía nuclear también plantea problemas medioambientales, incluida la seguridad y la eliminación de los residuos nucleares. Además de estas importantes consecuencias, las reservas de fuentes de energía no renovables son limitadas y, dado el rápido crecimiento de la tasa de consumo mundial de energía, pueden no durar más de unos cientos de años. Se está realizando un esfuerzo considerable para desarrollar y expandir el uso de fuentes de energía renovables, involucrando a un porcentaje significativo de los físicos e ingenieros del mundo.
La energía hidroeléctrica se produce al convertir la energía potencial gravitacional del agua que cae o fluye en energía cinética y luego en el trabajo para hacer funcionar generadores eléctricos o maquinaria. La conversión de la energía mecánica en las olas y mareas de la superficie del océano está en desarrollo. La energía eólica también convierte la energía cinética en trabajo, que puede usarse directamente para generar electricidad, operar molinos y propulsar veleros.
El interior de la Tierra tiene una gran cantidad de energía térmica, parte de la cual queda de su formación original (energía potencial gravitatoria convertida en energía térmica) y parte de la cual se libera de minerales radioactivos (una forma de energía nuclear natural).
Tomará mucho tiempo para que esta energía geotérmica escape al espacio, por lo que la gente generalmente la considera como una fuente renovable, cuando en realidad es inagotable en escalas de tiempo humanas.
La fuente de energía solar es la energía transportada por las ondas electromagnéticas radiadas por el Sol. La mayor parte de esta energía es transportada por la luz visible y la radiación infrarroja (calor). Cuando los materiales adecuados absorben las ondas electromagnéticas, la energía radiante se convierte en energía térmica, que puede usarse para calentar agua o, cuando se concentra, para producir vapor y generar electricidad (Figura 8.15). Sin embargo, en otro proceso físico importante, conocido como efecto fotoeléctrico, la radiación energética que incide sobre ciertos materiales se convierte directamente en electricidad. Los materiales que hacen esto se llaman fotovoltaicos. Algunos sistemas de energía solar usan lentes o espejos para concentrar los rayos del sol, antes de convertir su energía mediante energía fotovoltaica.

A medida que terminamos este capítulo sobre la energía y el trabajo, es relevante hacer algunas distinciones entre dos términos a veces mal entendidos en el área del uso de la energía. Como mencionamos anteriormente, la "ley de la conservación de la energía" es un principio muy útil para analizar los procesos físicos. No se puede probar a partir de principios básicos, pero es un muy buen dispositivo de contabilidad, y nunca se han encontrado excepciones. Establece que la cantidad total de energía en un sistema aislado siempre permanece constante. Relacionado con este principio, pero notablemente diferente de él, está la filosofía importante de la conservación de la energía. Este concepto tiene que ver con buscar disminuir la cantidad de energía utilizada por un individuo o grupo mediante la reducción de actividades (por ejemplo, bajar termostatos, conducir menos kilómetros) y/o aumentar las eficiencias de conversión en el
desempeño de una tarea particular, como el desarrollo y el uso de calentadores de ambiente más eficientes, automóviles con mayor calificación de millas por galón, luces fluorescentes compactas de bajo consumo, etc.
Dado que la energía en un sistema aislado no se destruye, crea ni genera, puedes preguntarte por qué debemos preocuparnos por nuestros recursos energéticos, ya que la energía es una cantidad conservada. El problema es que el resultado final de la mayoría de las transformaciones de energía es el calor residual, es decir, el trabajo que se ha "degradado" en la transformación de energía.
Momento lineal y colisiones
Video publicado en TikTok, en el canal @physicsisfun_official
Introducción

Los conceptos de trabajo, energía y el teorema del trabajo-energía son valiosos por dos razones principales: Primero, son poderosas herramientas computacionales, lo que hace que sea mucho más fácil analizar sistemas físicos complejos de lo que es posible usando las leyes de Newton directamente (por ejemplo, sistemas con fuerzas no constantes); y segundo, la observación de que la energía total de un sistema cerrado se conserva significa que el sistema solo puede evolucionar de manera consistente con la conservación de energía.
En otras palabras, un sistema no puede evolucionar al azar; solo puede cambiar de manera que se conserve la energía.
En este capítulo, desarrollamos y definimos otra cantidad conservada, llamada momentum lineal, y otra relación (el teorema impulso-momento), que impondrá una restricción adicional sobre cómo evoluciona un sistema en el tiempo.
La conservación del impulso es útil para comprender las colisiones, como la que se muestra en la imagen de arriba. Es igual de poderoso, igual de importante y tan útil como la conservación de la energía y el teorema del trabajo-energía.
Momento lineal
Nuestro estudio de la energía cinética mostró que una comprensión completa del movimiento de un objeto debe incluir tanto su masa como su velocidad ($K = (1/2)mv^2$). Sin embargo, por poderoso que sea este concepto, no incluye información sobre la dirección del vector de velocidad del objeto en movimiento. Definiremos ahora una cantidad física que incluye dirección.
Al igual que la energía cinética, esta cantidad incluye tanto masa como velocidad; como la energía cinética, es una forma de caracterizar la "cantidad de movimiento" de un objeto. Se le da el nombre de momento lineal o momentum (de la palabra latina movimentum, que significa "movimiento"), y está representado por el símbolo p.
El momentum p de un objeto es el producto de su masa y su velocidad: $$\bold{\vec{p}} = m\bold{\vec{v}}\tag{9.1}$$
Como se muestra en la Figura 9.2, el momento lineal es una cantidad vectorial (ya que la velocidad lo es). Esta es una de las cosas que hace que el momentum sea útil y no una duplicación de energía cinética.

Tal vez sea más útil para determinar si el movimiento de un objeto es difícil de cambiar (Figura 9.3) o fácil de cambiar (Figura 9.4).

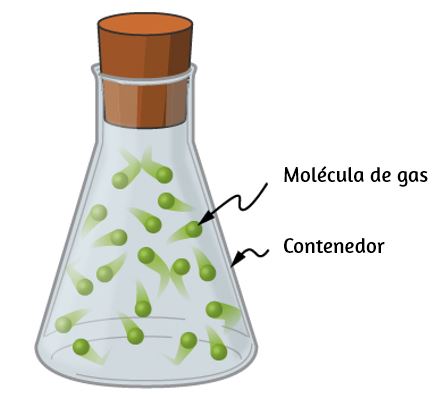
A diferencia de la energía cinética, el momentum depende igualmente de la masa y la velocidad de un objeto. Por ejemplo, como aprenderás cuando estudies termodinámica, la velocidad promedio de una molécula de aire a temperatura ambiente es de aproximadamente $500 m/s$, con una masa molecular promedio de $6 \times 10^{-25} kg$; su momentum es así
$$p_{molécula} = (6 \times 10^{-25} kg)(500 m/s) = 3 \times 10^{-22}kg\cdot m/s$$En comparación, un automóvil típico podría tener una velocidad de solo $15 m/s$, pero una masa de $1400 kg$, dándole un momentum deEn este capítulo usaremos como equivalentes, las expresiones momentum, momento lineal o simplemente la palabra momento.
$$p_{auto} = (1400 kg)(15 m/s) = 21,000 kg\cdot m/s$$¡Estos momentos son diferentes en $27$ órdenes de magnitud, o un factor de un billón de billones de billones!
Impulso y colisiones
Hemos definido el momento lineal como el producto de la masa y la velocidad. Por lo tanto, si la velocidad de un objeto debe cambiar (debido a la aplicación de una fuerza sobre el objeto), entonces necesariamente, su moementum cambia también. Esto indica una conexión entre el momento y la fuerza. El propósito de esta sección es explorar y describir esa conexión.
Supongamos que aplicas una fuerza sobre un objeto libre durante cierto tiempo. Claramente, cuanto mayor sea la fuerza, mayor será el cambio de momentum del objeto.
Alternativamente, cuanto más tiempo pases gastando esta fuerza, nuevamente, mayor será el cambio de momento, como se muestra en la Figura 9.5. La cantidad por la cual cambia el movimiento del objeto es, por lo tanto, proporcional a la magnitud de la fuerza, y también al intervalo de tiempo sobre el que se aplica la fuerza.
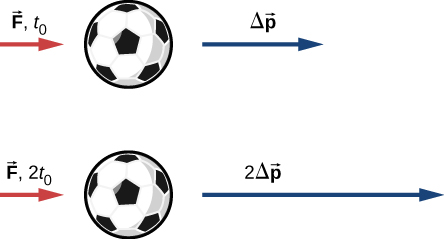
Matemáticamente, si una cantidad es proporcional a dos (o más) cosas, entonces es proporcional al producto de esas cosas. El producto de una fuerza y un intervalo de tiempo (sobre el que actúa esa fuerza) se llama impulso, y se le da el símbolo $\bold{\vec{J}}$.
Sea $\bold{\vec{F}}(t)$ la fuerza aplicada a un objeto durante un intervalo de tiempo diferencial $dt$ (Figura 9.6). El impulso resultante en el objeto se define como $$d\bold{\vec{J}} \equiv \bold{\vec{F}}(t)dt\tag{9.2}$$
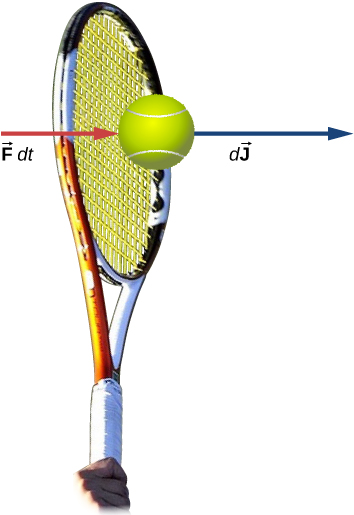
El impulso total en el intervalo $t_f - t_i$ es
Las ecuaciones 9.2 y 9.3 juntas dicen que cuando se aplica una fuerza para un intervalo de tiempo infinitesimal $dt$, causa un impulso infinitesimal $d\bold{\vec{J}}$, y el impulso total dado al objeto se define como la suma (integral) de todos estos impulsos infinitesimales.
Para calcular el impulso usando la Ecuación 9.3, necesitamos conocer la función de fuerza $F(t)$, que a menudo no lo hacemos. Sin embargo, un resultado del cálculo es útil aquí: recuerda que el valor promedio de una función en algún intervalo se calcula mediante
$$f(x)_{prom} = \frac{1}{\Delta x} \int_{x_i}^{x_f} f(x)dx$$donde $\Delta x = x_f - x_i$.
Aplicando esto a la función de fuerza dependiente del tiempo, obtenemosPor lo tanto, de la Ecuación 9.3,
La idea aquí es que puedes calcular el impulso sobre el objeto incluso si no conoces los detalles de la fuerza en función del tiempo; solo necesitas la fuerza promedio. De hecho, sin embargo, el proceso generalmente se invierte: tu determinas el impulso (por medición o cálculo) y luego calculas la fuerza promedio que causó ese impulso.
Para calcular el impulso, se obtiene un resultado útil al escribir la fuerza en la ecuación 9.3 como $\bold{\vec{F}}(t) = m\bold{\vec{a}}(t)$:
$$\bold{\vec{J}} = \int_{t_i}^{t_f} \bold{\vec{F}} (t)dt = m\int_{t_i}^{t_f} \bold{\vec{a}}(t)dt = m[\bold{\vec{v}}(t_f) − \bold{\vec{v}}(t_i)]$$Para una fuerza constante $\bold{\vec{F}}_{prom} = \bold{\vec{F}} = m\bold{\vec{a}}$, esto se simplifica a
$$\bold{\vec{J}} = m\bold{\vec{a}} \Delta t = m\bold{\vec{v}}_f − m\bold{\vec{v}}_i = m(\bold{\vec{v}}_f − \bold{\vec{v}}_i)$$Esto es
$$\bold{\vec{J}} = m\Delta \bold{\vec{v}}$$Ten en cuenta que la forma integral, Ecuación 9.3, también se aplica a las fuerzas constantes; en ese caso, dado que la fuerza es independiente del tiempo, sale de la integral, que luego puede evaluarse trivialmente.
Ejemplo 9.1
El cráter del Meteoro de Arizona
Aproximadamente hace $$50,000$ años, un meteorito de hierro y níquel grande (radio de $25 m$) colisionó con la Tierra a una velocidad estimada de $1,28 \times 10^4 m/s$ en lo que ahora es el desierto del norte de Arizona, en los Estados Unidos. El impacto produjo un cráter que aún es visible hoy en día (Figura 9.7); tiene aproximadamente $1200 m$ (tres cuartos de milla) de diámetro, $170 m$ de profundidad, y tiene un borde que se eleva $45 m$ por encima de la planicie desértica circundante. Los meteoritos de hierro y níquel suelen tener una densidad de $\rho = 7970 kg/m^3$.
Usa las consideraciones de impulso para estimar la fuerza promedio y la fuerza máxima que el meteorito aplicó a la Tierra durante el impacto.

Estrategia
Es conceptualmente más fácil revertir la pregunta y calcular la fuerza que la Tierra aplicó al meteoro para detenerlo. Por lo tanto, calcularemos la fuerza sobre el meteoro y luego usaremos la tercera ley de Newton para argumentar que la fuerza del meteoro en la Tierra fue igual en magnitud y opuesta en la dirección.
Usando los datos dados sobre el meteoro, y haciendo conjeturas razonables sobre la forma del meteoro y el tiempo de impacto, primero calculamos el impulso usando la Ecuación 9.6. Luego usamos la relación entre fuerza e impulso (Ecuación 9.5) para estimar la fuerza promedio durante el impacto.
A continuación, seleccionamos una función de fuerza razonable para el evento de impacto, calculamos el valor promedio de esa función (Ecuación 9.4) y establecemos que la expresión resultante es igual a la fuerza promedio calculada. Esto nos permite hallar la fuerza máxima.
Solución
Define hacia arriba como la dirección y positiva. Para simplificar, supón que el meteoro viaja verticalmente hacia abajo antes del impacto. En ese caso, su velocidad inicial es $\bold{\vec{v}}_i = -v_i \^{\bold{j}}$, y la fuerza que ejerce la Tierra sobre los puntos del meteoro hacia arriba,
$\bold{\vec{F}}(t) = + F(t) \^{\bold{j}}$. La situación en t = 0 se representa a continuación.
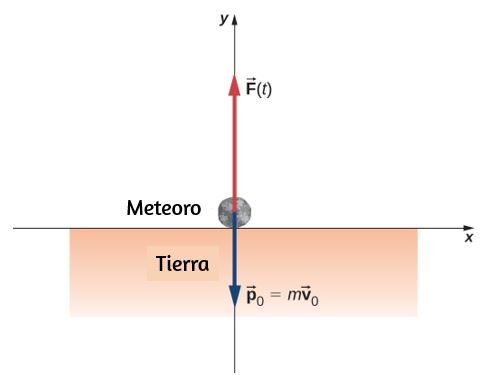
De la ecuación 9.6, $\bold{\vec{F}} = m \Delta \bold{\vec{v}}$, entonces tenemos
$$\bold{\vec{F}}_{prom} = \frac{m\Delta \bold{\vec{v}}}{\Delta t}$$La masa es igual al producto de la densidad del meteoro y su volumen:
$$m = \rho V$$Si asumimos que el meteorito era más o menos esférico, tenemos
$$V = \frac43 \pi R^3$$Así obtenemos
$$\bold{\vec{F}}_{prom} = \frac{\rho V\Delta \bold{\vec{v}}}{\Delta t} = \frac{\rho(4/3)\pi R^3(\bold{\vec{v}}_f - \bold{\vec{v}}_i)}{\Delta t}$$El problema dice que la velocidad en el impacto fue $-1.28 \times 10^4 m/s\^{\bold{j}}$ (la velocidad final es cero); también, suponemos que el impacto primario duró aproximadamente $t_{max} = 2s$. Sustituyendo estos valores obtenemos:
$$\begin{split} \bold{\vec{F}}_{prom} &= \frac{(7970 kg/m^3)[4/3\pi (25 m)^3][0 m/s − (−1.28\times 10^4 m/s \^{\bold{j}})]}{2s}\\ &= +(3.33 \times 10^{12} N)\^{\bold{j}} \end{split}$$Esta es la fuerza promedio aplicada durante la colisión.
Observa que este vector de fuerza apunta en la misma dirección que el cambio del vector de velocidad $\Delta \bold{\vec{v}}$.
A continuación, calculamos la fuerza máxima. El impulso está relacionado con la función de fuerza por
$$\bold{\vec{J}} = \int_{t_1}^{t_{max}} \bold{\vec{F}}(t)dt$$Necesitamos hacer una elección razonable para la fuerza en función del tiempo. Definimos $t = 0$ como el momento en que el meteorito toca el suelo por primera vez. Entonces suponemos que la fuerza es máxima en el impacto y rápidamente cae a cero. Una función que hace esto es
$$F(t) = F_{max} e^{-t^2/(2\tau^2)}$$(El parámetro $\tau$ representa la rapidez con que la fuerza disminuye a cero). La fuerza promedio es
$$\bold{\vec{F}}-{prom} = \frac{1}{\Delta t} \int_0^{t_{max}}F_{máx} e^{-t^2/(2\tau ^2)}dt$$donde $\Delta t = t_{máx} - 0 s$. Como ya tenemos un valor numérico para $F_{prom}$, podemos usar el resultado de la integral para obtener $F_{máx}$.
Elegir $\tau = \frac{1}{e} t_{max}$ (esta es una opción común, como verás en los capítulos posteriores), y adivinar que $t_{max} = 2s$, esta integral se evalúa como
$$F_{prom} = 0.458F_{max}$$Por lo tanto, la fuerza máxima tiene una magnitud de
$$0.458F_{max} = 3.33 \times 10^{12} N$$ $$F_{max} = 7.27 \times 10^{12} N$$La función de fuerza completa, incluida la dirección, es
$$\bold{\vec{F}}(t) = (7.27 \times 10^{12} N)e^{-t^2/(8 s^2)}\^{\bold{j}}$$Esta es la fuerza que la Tierra aplicó al meteoro; según la tercera ley de Newton, la fuerza que el meteorito aplica a la Tierra es
$$\bold{\vec{F}}(t) = -(7.27 \times 10^{12} N)e^{-t^2(8 s^2)}\^{\bold{j}}$$Explicación
El gráfico de esta función contiene información importante. Vamos a graficar (la magnitud de) tanto esta función como la fuerza promedio juntas (Figura 9.8).
Observa que el área debajo de cada gráfico se ha rellenado. Para el gráfico de la fuerza (constante) $F_{prom}$, el área es un rectángulo, correspondiente a $F_{prom}\Delta t = J$. En cuanto a la representación de $F(t)$, recuerda del cálculo que el área bajo la representación de una función es numéricamente igual a la integral de esa función, durante el intervalo especificado; entonces aquí, eso es $\displaystyle\int_0^{t_{max}} F(t)dt = J$$
Por lo tanto, las áreas son iguales, y ambas representan el impulso que el meteorito aplicó a la Tierra durante el impacto de dos segundos. La fuerza promedio en la Tierra suena como una gran fuerza, y lo es.
Sin embargo, la Tierra apenas lo notó. La aceleración que obtuvo la Tierra fue solo
$$\bold{\vec{a}} = \frac{-\bold{\vec{F}}_{prom}}{M_{tierra}} = \frac{−(3.33 \times 10^{12} N) \^{\bold{j}}}{5.97 \times 10^{24} kg} = −(5.6 \times 10^{−13} m/s^2)\^{\bold{j}}$$que es completamente inconmensurable. Dicho esto, el impacto creó ondas sísmicas que hoy en día podrían ser detectadas por modernos equipos de monitoreo.
Las preocupaciones en torno a las colisiones con asteroides mantienen en alerta a científicos de todo el mundo.
La Universidad de Purdue ha diseñado un programa (Earth Impact Effects) para estimar las consecuencias ambientales de un cometa o impacto de un asteroide en la Tierra. El programa requiere seis entradas: diámetro del intruso galáctico, densidad, velocidad de impacto antes de la entrada atmosférica, ángulo de impacto, la distancia desde el impacto al que se deben calcular los efectos ambientales y el tipo de objetivo (roca sedimentaria, roca cristalina o una capa de agua sobre la roca). Se ilustra la utilidad del programa examinando las consecuencias ambientales previstas en los Estados Unidos de hipotéticos escenarios de impacto ocurriendo en Los Angeles. El efecto más devastador es la radiación térmica.
Hacemos un alto en nuestra ruta de aprendizaje, con un clon de un juego clásico de la empresa Atari, "Asteroids"Asteroids es un popular videojuego de arcade basado en vectores lanzado en 1979 por Atari. El objetivo del juego es disparar y destruir asteroides evitando chocar contra los fragmentos de estos. Fue uno de los juegos más populares de la Época Dorada de los videojuegos arcade. Asteroids fue inspirado por el juego Spacewar! (Wikipedia).. Haz clic sobre el juego y luego usa las teclas de dirección y la barra espaciadora. Esta emulación fue diseñada por Michael Waterworth.
Ejemplo 9.2
Los beneficios del impulso
Un automóvil que viaja a $27 m/s$ colisiona con un edificio. La colisión con el edificio hace que el automóvil se detenga en aproximadamente $1$ segundo. El conductor, que pesa $860 N$, está protegido por una combinación de cinturón de seguridad de tensión variable y una bolsa de aire (Figura 9.9). (En efecto, el conductor colisiona con el cinturón de seguridad y el airbag y no con el edificio.) El airbag y el cinturón de seguridad disminuyen su velocidad, de modo que se detiene en aproximadamente $2,5 s.$).
a. ¿Qué fuerza promedio experimenta el conductor durante la colisión?
b. Sin el cinturón de seguridad y el airbag, el tiempo de colisión (con el volante) habría sido de aproximadamente $0,20 s$. ¿Qué fuerza experimentaría en este caso?

Estrategia
a. Se nos da el peso del conductor, sus velocidades iniciales y finales, y el momento de la colisión; se nos pide que calculemos una fuerza. El impulso parece la forma correcta de abordar esto; podemos combinar la Ecuación 9.5 y la Ecuación 9.6.
Solución
a. Define la dirección $x+$ como la dirección en la que el automóvil se está moviendo inicialmente. Sabemos que
$$\bold{\vec{j}} = \bold{\vec{F}}\Delta t\;\text{ y, además, }\;\bold{\vec{J}} = m\Delta \bold{\vec{v}}$$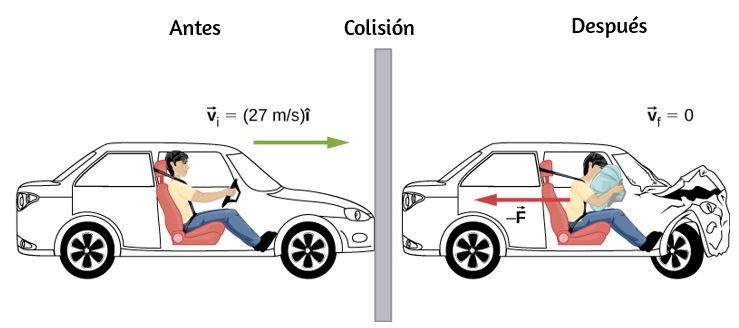
Igualando las dos expresiones anteriores, obtenemos:
$$\bold{\vec{F}}\Delta t = m\Delta \bold{\vec{v}}$$Necesitamos convertir este peso a la masa equivalente, expresada en unidades del SI:
$$\frac{860 N}{9.8 m/s^2} = 87.8 kg$$Recordando que $\Delta\bold{\vec{v}} = \bold{\vec{v}}_f - \bold{\vec{v}}_i$, y notando que la velocidad final es cero, hallamos la fuerza:
$$\bold{\vec{F}} = m\frac{0 - v_i\^{\bold{i}}}{\Delta t} = (87.8kg)\Big(\frac{−(27m/s)\^{\bold{i}}}{2.5 s}\Big) = −(948 N)\^{\bold{i}}$$El signo negativo implica que la fuerza lo ralentiza. Para la perspectiva, esto es aproximadamente 1,1 veces su propio peso.
b. Es el mismo cálculo, solo el intervalo en tiempo diferente:
$$\bold{\vec{F}} = (87.8kg)\Big(\frac{−(27m/s)\^{\bold{i}}}{0.20 s}\Big) = −(11,853 N)\^{\bold{i}}$$que es aproximadamente $14$ veces su propio peso. ¡Gran diferencia!
Explicación
Observa que el valor de un airbag es por la reducción de la fuerza en los ocupantes del vehículo. Por esta razón, se han requerido en todos los vehículos de pasajeros en los Estados Unidos desde 1991, y han sido un lugar común en toda Europa y Asia desde mediados de la década de 1990. El cambio de momento en un choque es el mismo, con o sin un airbag; la fuerza, sin embargo, es muy diferente.
Efecto del Impulso
Como un impulso es una fuerza que actúa durante cierto tiempo, hace que el movimiento de un objeto cambie. Retomando la ecuación 9.6:
$$\bold{\vec{J}} = m\Delta \bold{\vec{v}}$$Debido a que $m\bold{\vec{v}}$ es el impulso de un sistema, $m\Delta \bold{\vec{v}}$ es el cambio de momento $\Delta \bold{\vec{p}}$.
Esto nos da la siguiente relación, llamada el "teorema impulso-momento".
Un impulso aplicado a un sistema cambia el momento del sistema, y ese cambio de momento es exactamente igual al impulso que se aplicó: $$\bold{\vec{J}} = \Delta \bold{\vec{p}}\tag{9.7}$$
El teorema impulso-momento se representa gráficamente en la figura 9.10.
Hay dos conceptos cruciales en el teorema de impulso-momento:
- El impulso es una cantidad vectorial; un impulso de, digamos, $- (10 N\cdot s)\^{\bold{i}}$ es muy diferente de un impulso de $+ (10 N\cdot s)\^{\bold{i}}$, pues causan cambios de impulso completamente opuestos.
- Un impulso no causa momento, más bien, causa un cambio en el momento de un objeto. Por lo tanto, debes restar el momento final del momento inicial, y dado que el momento también es una cantidad vectorial, debes tener en cuenta cuidadosamente los signos de los vectores de momento.
Las preguntas más frecuentes formuladas en relación con el impulso son calcular la fuerza aplicada, o el cambio de velocidad que ocurre como resultado de la aplicación de un impulso.
El enfoque general es el mismo.
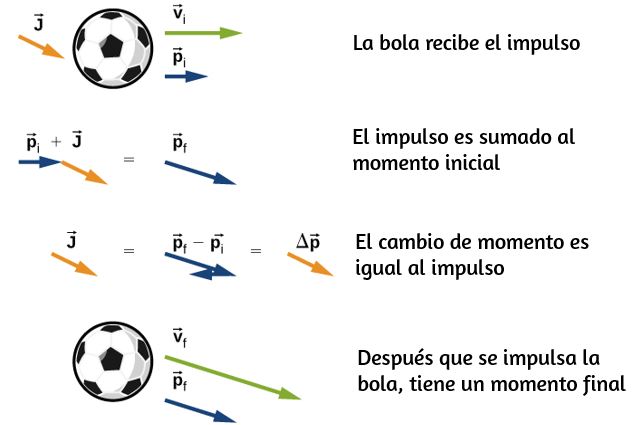
1. Expresa el impulso como una fuerza multiplicado por el intervalo de tiempo relevante.
2. Expresa el impulso como el cambio de momento, generalmente como $m\Delta v$.
3. Iguala esto y halla la cantidad deseada.
Ejemplo 9.3
Moviendo el Enterprise

"Señor Sulu, sáquenos, adelante un cuarto de impulso". Con este comando, el Capitán Kirk de la nave espacial Enterprise (Figura 9.11) hace que su nave comience desde el reposo hasta una velocidad final de $v_f = 1/4(3.0 \times 10^8 m/s)$. Suponiendo que esta maniobra se complete en $60 s$, ¿qué fuerza promedio aplicaron los motores de impulso a la nave?
Estrategia
Nos piden una fuerza, sabemos las velocidades inicial y final (y, por lo tanto, el cambio en la velocidad), y sabemos el intervalo de tiempo durante el cual sucedió todo esto.
En particular, sabemos la cantidad de tiempo que actuó la fuerza. Esto sugiere usar la relación o teorema impulso-momento. Para usarlo, sin embargo, necesitamos la masa de la Enterprise. Una búsqueda en Internet da una mejor estimación de la masa de la Enterprise (en la película de 2009) como $2 \times 10^9 kg$.
Solución
Debido a que este problema involucra solo una dirección (es decir, la dirección de la fuerza aplicada por los motores), solo necesitamos la forma escalar del teorema del impulso-momento Ecuación 9.7, que es
$$\Delta p = J,\;\text{ con }\; \Delta p = m\Delta v\;\text{ y }\;J = F\Delta t$$Igualando estas expresiones, obtenemos:
$$F\Delta t= m\Delta v$$La resolución de la magnitud de la fuerza y la inserción de los valores dados conduce a
$$F = \frac{m\Delta v}{\Delta t} = \frac{(2 \times 10^9 kg)(7.5 \times 10^7 m/s)}{60 s} = 2.5 \times 10^{15} N$$Explicación
Esta es una fuerza inmensamente inimaginable. Casi no hace falta decir que tal fuerza mataría a todos a bordo al instante, además de destruir todas las piezas del equipo. Afortunadamente, la empresa tiene "amortiguadores inerciales". Se deja como un ejercicio para que la imaginación del lector determine cómo funcionan.
 Comprueba tu aprendizaje 9.1
Comprueba tu aprendizaje 9.1
Ejemplo 9.4
El iPhone cayendo
Apple lanzó su iPhone 6 Plus en noviembre de 2014. Según muchos informes, originalmente se suponía que tenía una pantalla hecha de zafiro, pero eso fue cambiado en el último minuto por una pantalla de vidrio endurecido. Según se informa, esto se debió a que la pantalla de zafiro se rompió cuando se cayó el teléfono. ¿Qué fuerza experimentó el iPhone 6 Plus como resultado de su lanzamiento?
Estrategia
La fuerza que experimenta el teléfono se debe al impulso que le aplica el piso cuando el teléfono colisiona con el piso. Nuestra estrategia entonces es usar la relación impulso-momento. Calculamos el impulso, estimamos el tiempo de impacto y lo usamos para calcular la fuerza.
Necesitamos hacer un par de estimaciones razonables, así como buscar datos técnicos del teléfono. Primero, supongamos que el teléfono se cae con más frecuencia desde la altura del pecho en una persona de estatura promedio.
En segundo lugar, supongamos que se abandona desde el reposo, es decir, con una velocidad vertical inicial de cero. Finalmente, suponemos que el teléfono rebota muy poco: se supone que la altura de su rebote es insignificante.
Solución
Define hacia arriba la dirección y positiva. Una altura típica es aproximadamente $h = 1.5 m$ y, como se dijo, $\bold{\vec{v}}_ = (0 m/s)\^{\bold{i}}$. La fuerza promedio en el teléfono está relacionada con el impulso que el piso aplica sobre él durante la colisión:
$$\bold{\vec{F}}_{prom} = \frac{\bold{\vec{J}}}{\Delta t}$$El impulso $\bold{\vec{J}}$ es igual al cambio en el momento,
$$\bold{\vec{J}} = \Delta \bold{\vec{p}}$$Entonces:
$$\bold{\vec{v}}_{prom} = \frac{\Delta \bold{\vec{p}}}{\Delta t}$$El cambio de momento es
$$\Delta \bold{\vec{p}} = m\Delta \bold{\vec{v}}$$Necesitamos tener cuidado con las velocidades aquí, pues este es el cambio de velocidad debido a la colisión con el piso. Pero el teléfono también tiene una velocidad de caída inicial $\bold{\vec{v}}_i = (0 m/s)\^{\bold{j}}$, por lo que etiquetamos nuestras velocidades:
- $\bold{\vec{v}}_i$: la velocidad inicial con la que se cayó el teléfono (cero, en este ejemplo)
- $\bold{\vec{v}}_1$: la velocidad con la que el teléfono tuvo el instante justo antes de tocar el piso
- $\bold{\vec{v}}_2$: la velocidad final del teléfono como resultado de golpear el piso
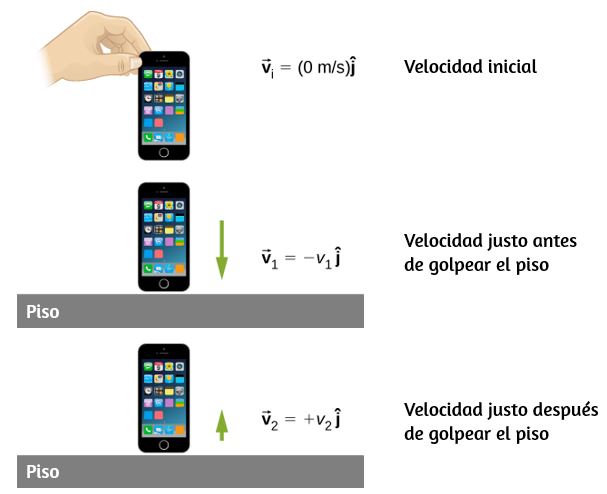
La Figura 9.12 muestra las velocidades en cada uno de estos puntos en la trayectoria del teléfono.
Con estas definiciones, el cambio de momento del teléfono durante la colisión con el piso es
$$m\Delta \bold{\vec{v}} = m(\bold{\vec{v}}_2 - \bold{\vec{v}}_1)$$Como suponemos que el teléfono no rebota en absoluto cuando toca el suelo (o al menos, la altura de rebote es insignificante), entonces $\bold{\vec{v}}_2$ es cero, por lo que
$$\begin{split} m\Delta \bold{\vec{v}} &= m[0 − (−v_1\^{\bold{j}})]\\ &= +mv_1\^{\bold{j}} \end{split}$$Podemos obtener la velocidad del teléfono justo antes de que toque el piso usando la cinemática o la ley de la conservación de la energía. Utilizaremos la conservación de la energía aquí, deberías volver a hacer esta parte del problema usando la cinemática y demostrar que obtienes la misma respuesta.
Primero, define el cero de la energía potencial que se ubicará en el piso. La conservación de la energía nos da:
$$E_i = E_1\\ K_i + U_i = K_1 + U_1\\ \frac12 mv_i^2 + mgh_{caída} = \frac12 mv_1^2 + mgh_{piso}$$Definiendo $h_{piso} = 0$ y usando $\bold{\vec{v}}_i = (0 m/s)\^{\bold{j}}$ obtenemos:
$$\frac12 mv_1^2 = mgh_{caída}$$Como $v_1$ es una magnitud vectorial, debe ser positiva. Por lo tanto, $m\Delta \bold{\vec{v}} = mv_1 = \sqrt{2gh_{caída}}$. Al insertar este resultado en la expresión de fuerza, obtenemos:
$$\bold{\vec{F}} = \frac{\Delta \bold{\vec{p}}}{\Delta t} = \frac{m\Delta \bold{\vec{v}}}{\Delta t} = \frac{+mv_1\^{\bold{j}}}{\Delta t} = \frac{m\sqrt{2gh}}{\Delta t}\^{\bold{j}}$$Finalmente, necesitamos estimar el tiempo de colisión. Una forma común de estimar el tiempo de colisión es calcular cuánto demoraría el objeto en recorrer su propia longitud. El teléfono se mueve a $5.4 m/s$ justo antes de tocar el piso, y tiene una longitud de $0.14 m$, dando un tiempo de colisión estimado de $0.026 s$. Al reemplazar los datos dados, obtenemos
$$\bold{\vec{F}} = \frac{(0.172 kg)\sqrt{2(9.8 m/s^2)(1.5 m)}}{0.026 s}\^{\bold{j}} = (36 N)\^{\bold{j}}$$Explicación
El iPhone pesa solo $(0.172 kg)(9.81 m/s^2) = 1.68N$, la fuerza que aplica el suelo es, por lo tanto, más de 20 veces su peso.
 Comprueba tu aprendizaje 9.2
Comprueba tu aprendizaje 9.2
Momento y fuerza
En el ejemplo 9.3, obtuvimos una relación importante:
En otras palabras, la fuerza promedio aplicada a un objeto es igual al cambio del momento que causa la fuerza, dividido por el intervalo de tiempo durante el cual ocurre este cambio de momento. Esta relación es muy útil en situaciones donde el tiempo de colisión $\Delta t$ es pequeño, pero medible; los valores típicos serían $1/10$ de un segundo, o incluso una milésima de segundo. Los choques automovilísticos, el lanzamiento de una pelota de fútbol o las colisiones de partículas subatómicas cumplirían este criterio.
Para un momento continuamente cambiante, debido a una fuerza continuamente cambiante, esto se convierte en una poderosa herramienta conceptual. En el límite $\Delta t \to dt$, la ecuación 9.2 se convierte en:
Esto dice que la tasa de cambio del momento del sistema (lo que implica que el momento es una función del tiempo) es exactamente igual a la fuerza neta aplicada (también, en general, una función del tiempo). Esta es, de hecho, la segunda ley de Newton, escrita en términos de momento en lugar de aceleración.
Esta es la relación que el propio Newton presentó en su Principia Mathematica (aunque lo llamó "cantidad de movimiento" en lugar de "momento").
Si la masa del sistema permanece constante, la ecuación 9.3 se reduce a la forma más familiar de la segunda ley de Newton. Podemos ver esto sustituyendo la definición de momento:
$$\bold{\vec{F}} = \frac{d(m\bold{\vec{v}})}{dt} = m\frac{d}{dt} = m\bold{\vec{a}}$$La suposición de masa constante nos permitió sacar m de la derivada. Si la masa no es constante, no podemos usar esta forma de la segunda ley, sino que debemos comenzar desde la ecuación 9.3. Por lo tanto, una de las ventajas de expresar la fuerza en términos de cambio de momento es que permite cambiar la masa del sistema, así como la velocidad; este es un concepto que exploraremos cuando estudiemos el movimiento de los cohetes.
La fuerza externa neta en un sistema es igual a la tasa de cambio del momento de ese sistema causado por la fuerza: $$\bold{\vec{F}} = \frac{d\bold{\vec{p}}}{dt}$$
Aunque la ecuación 9.3 permite cambiar la masa, la relación entre momento y fuerza sigue siendo útil cuando la masa del sistema es constante, como en el siguiente ejemplo.
Ejemplo 9.5
Calculando una fuerza: Servicio de tenis de Venus Williams
Durante el Abierto de Francia de 2007, Venus Williams conectó el servicio más rápido registrado en un partido femenino de primer nivel, alcanzando una velocidad de $58 m/s$ ($209 km/h$). ¿Cuál es la fuerza promedio ejercida sobre la pelota de tenis de $0,057 kg$ por la raqueta de Venus Williams? Supón que la velocidad de la bola justo después del impacto es de $58 m/s$, como se muestra en la figura 9.13, que la componente horizontal inicial de la velocidad antes del impacto es despreciable y que la bola permaneció en contacto con la raqueta durante 5.0 ms.
Estrategia
Este problema involucra solo una dimensión porque la pelota comienza sin tener un componente de velocidad horizontal antes del impacto. La segunda ley de Newton declarada en términos de momento se escribe como
$$\bold{\vec{F}} = \frac{d\bold{\vec{p}}}{dt}$$Como se señaló anteriormente, cuando la masa es constante, el cambio en el momento está dado por
$$\Delta p = m\Delta v = m(v_f - v_i)$$donde hemos usado escalares porque este problema involucra solo una dimensión. En este ejemplo, se dan la velocidad justo después del impacto y el intervalo de tiempo;
por lo tanto, una vez que $\Delta p$ se calcula, podemos usar $F = \frac{\Delta p}{\Delta t}$ para encontrar la fuerza.

Solución
Para determinar el cambio en el momento, sustituye los valores para las velocidades inicial y final en la ecuación anterior:
$$\Delta p = m(v_f - v_i) = (0.057 kg)(58 m/s − 0 m/s) = 3.3 kg\cdot m/s$$Ahora la magnitud de la fuerza externa neta se puede determinar mediante el uso de
$$F = \frac{\delta p}{\Delta t} = \frac{3.3 kg\cdot m/s}{5.0 \times 10^{−3} s} = 6.6 \times 10^2 N$$donde hemos retenido solo dos cifras significativas en el paso final.
Explicación
Esta cantidad fue la fuerza promedio ejercida por la raqueta de Venus Williams sobre la pelota de tenis durante su breve impacto (nótese que la bola también experimentó la fuerza de gravedad de $0,57 N$, pero esa fuerza no se debió a la raqueta). Este problema también podría resolverse encontrando primero la aceleración y luego usando F = ma, pero se requeriría un paso adicional en comparación con la estrategia utilizada en este ejemplo.
Conservación del momento lineal
Recuerda la tercera ley de Newton: cuando dos objetos de masas $m_1$ y $m_2$ interactúan (lo que significa que se aplican fuerzas entre sí), la fuerza que el objeto $2$ aplica al objeto $1$ es igual en magnitud y opuesta en dirección a la fuerza a la que aplica el objeto $1$ al objeto $2$:
- $\bold{\vec{F}}_{21}$: la fuerza en $m_1$ desde $m_2$
- $\bold{\vec{F}}_{12}$: la fuerza en $m_2$ desde $m_1$
Luego, en símbolos, la tercera ley de Newton dice
$$\bold{\vec{F}}_{21} = -\bold{\vec{F}}_{12}\\ m_1\bold{\vec{a}}_1 = -m_2\bold{\vec{a}}_2$$Recuerda que estas dos fuerzas no se cancelan porque se aplican a diferentes objetos. $F_{21}$ hace que $m_1$ se acelere, y $F_{12}$ hace que $m_2$ también se acelere).
Aunque las magnitudes de las fuerzas sobre los objetos son las mismas, las aceleraciones no lo son, simplemente porque las masas (en general) son diferentes. Por lo tanto, los cambios en la velocidad de cada objeto son diferentes:
$$\frac{d\bold{\vec{v}}_1}{dt} \ne \frac{d\bold{\vec{v}}_2}{dt}$$Sin embargo, los productos de la masa y el cambio de velocidad son iguales (en magnitud):
Es una buena idea, en este punto, asegurarse de tener claro el significado físico de las derivadas en la Ecuación 9.3. Debido a la interacción, cada objeto termina obteniendo su velocidad cambiada, en una cantidad $dv$.
Además, la interacción se produce durante un intervalo de tiempo $dt$, lo que significa que el cambio de velocidades también se produce en dt. Este intervalo de tiempo es el mismo para cada objeto.
Supongamos, por el momento, que las masas de los objetos no cambian durante la interacción. En ese caso, podemos extraer las de las derivadas:
Por lo tanto,
Esto dice que la velocidad a la que cambia el momento es la misma para ambos objetos. Las masas son diferentes, y los cambios de velocidad son diferentes, pero la tasa de cambio del producto de $m$ y $\bold{\vec{v}}$ es la misma.
Físicamente, esto significa que durante la interacción de los dos objetos ($m_1$ y $m_2$), se cambia el momento de ambos objetos; pero esos cambios son idénticos en magnitud, aunque de signo opuesto.
Por ejemplo, el momento del objeto $1$ podría aumentar, lo que significa que el momento del objeto $2$ disminuye exactamente en la misma cantidad.
A la luz de esto, volvamos a escribir la Ecuación 9.12 en una forma más sugerente:
Esto dice que durante la interacción, aunque el momento del objeto $1$ cambia, y el momento del objeto $2$ también cambia, estos dos cambios se cancelan entre sí, de modo que el cambio total de momento de los dos objetos juntos es cero.
Como el momento total combinado de los dos objetos juntos nunca cambia, entonces podríamos escribir
de lo cual se deduce que
Como se muestra en la figura 9.14, el momento total del sistema antes y después de la colisión sigue siendo el mismo.
Al generalizar este resultado para $N$ objetos, obtenemos
La ecuación 9.17 es la definición del momento total (o neto) de un sistema de N objetos que interactúan, junto con la afirmación de que el momento total de un sistema de objetos es constante en el tiempo o, mejor aún, se conserva.
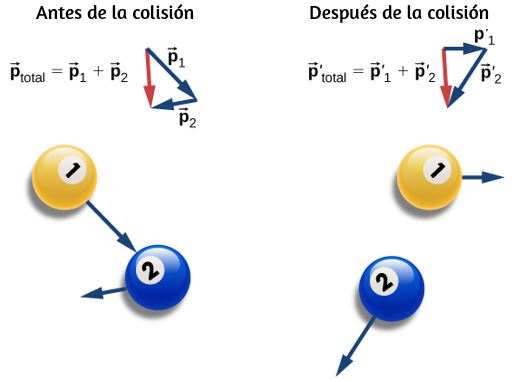
Si el valor de una cantidad física es constante en el tiempo, decimos que la cantidad se conserva.
Requisitos para la conservación Momentum
Hay una complicación, sin embargo. Un sistema debe cumplir dos requisitos para que se conserve su impulso:
- La masa del sistema debe permanecer constante durante la interacción.
A medida que los objetos interactúan (se aplican fuerzas entre sí), pueden transferir masa de uno a otro; pero cualquier ganancia de un objeto en masa se equilibra con la pérdida de esa masa de otro. La masa total del sistema de objetos, por lo tanto, se mantiene sin cambios a medida que pasa el tiempo: $$\Big[\frac{dm}{dt}\Big]_{sistema} = 0$$ - La fuerza externa neta en el sistema debe ser cero.
Cuando los objetos colisionan o explotan y se mueven, ejercen fuerzas el uno sobre el otro. Sin embargo, todas estas fuerzas son internas al sistema, y así cada una de estas fuerzas internas se equilibran con otra fuerza interna que es igual en magnitud y opuesta en signo. Como resultado, el cambio en el momento causado por cada fuerza interna es cancelado por otro cambio de momento que es igual en magnitud y opuesto en la dirección. Por lo tanto, las fuerzas internas no pueden cambiar el momento total de un sistema porque los cambios suman cero. Sin embargo, si hay alguna fuerza externa que actúa sobre todos los objetos (gravedad, por ejemplo, o fricción), entonces esta fuerza cambia el momento del sistema como un todo. Por lo tanto, para que se conserve el impulso del sistema, debemos tener
Se dice que un sistema de objetos que cumple estos dos requisitos es un sistema cerrado (también llamado sistema aislado). Por lo tanto, la forma más compacta de expresar esto se muestra a continuación.
El momento total de un sistema cerrado se conserva: $$\sum_{j=1}^N \bold{\vec{p}}_j = \text{constante}$$
Esta declaración se llama Ley de Conservación del Momento. Junto con la conservación de la energía, es uno de los fundamentos sobre los que se encuentra toda la física. Toda nuestra evidencia experimental respalda esta afirmación: desde los movimientos de los cúmulos galácticos hasta los quarks que forman el protón y el neutrón, y en todas las escalas intermedias. En un sistema cerrado, el momento total nunca cambia.
Ten en cuenta que absolutamente puede haber fuerzas externas que actúen en el sistema; pero para que el momento del sistema permanezca constante, estas fuerzas externas tienen que cancelarse, de modo que la fuerza externa neta sea cero. Las bolas de billar en una mesa tienen una fuerza de peso que actúa sobre ellas, pero las pesas están equilibradas (canceladas) por las fuerzas normales, por lo que no hay fuerza neta.
Practica en la siguiente escena interactiva, diseñada por Michele Mottini (cambia los tipos de movimiento en la opción test).
RPool
El significado de 'sistema'
Un sistema (mecánico) es la colección de objetos en cuyo movimiento (cinemática y dinámica) estás interesado. Si estás analizando el rebote de una pelota en el suelo, probablemente solo te interese el movimiento de la pelota, y no de la Tierra; por lo tanto, la pelota es tu sistema.
Si estás analizando un accidente automovilístico, los dos automóviles juntos componen tu sistema (Figura 9.15).
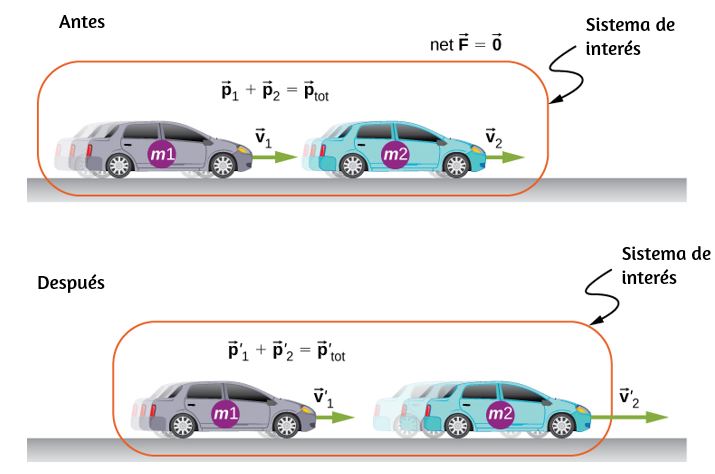
El uso de la conservación del momento requiere cuatro pasos básicos. El primer paso es crucial:
- Identifica un sistema cerrado (la masa total es constante, ninguna fuerza externa neta actúa en el sistema).
- Escribe una expresión que represente el momento total del sistema antes del "evento" (explosión o colisión).
- Escribe una expresión que represente el momento total del sistema después del "evento".
- Establece estas dos expresiones iguales entre sí, y resuelve esta ecuación para la cantidad deseada.
Ejemplo 9.6
Carros colisionantes
Dos carros en un laboratorio de física ruedan en una pista nivelada, con una fricción insignificante. Estos carros tienen pequeños imanes en sus extremos, de modo que cuando colisionan, se unen (Figura 9.16). El primer carro tiene una masa de $675$ gramos y está rodando a $0.75 m/s$ a la derecha; el segundo tiene una masa de $500$ gramos y está rodando a $1,33 m/s$, también a la derecha. Después de la colisión, ¿cuál es la velocidad de los dos carros unidos?

Estrategia
Tenemos una colisión. Nos dan masas y velocidades iniciales; se nos pide la velocidad final. Todo esto sugiere utilizar la conservación del momento como método de solución.
Sin embargo, solo podemos usarlo si tenemos un sistema cerrado. Entonces, debemos asegurarnos de que el sistema que elijamos no tenga una fuerza externa neta y que la colisión no cambie su masa.
Definir el sistema como los dos carros cumple con los requisitos para un sistema cerrado: la masa combinada de los dos carros ciertamente no cambia, y aunque los carros definitivamente ejercen fuerzas el uno sobre el otro, esas fuerzas son internas al sistema, entonces no cambia el momento del sistema como un todo. En la dirección vertical, los pesos de los carros son cancelados por las fuerzas normales en los carros de la pista.
Solución
La conservación del momento es
$$\bold{\vec{p}}_f = \bold{\vec{p}}_i$$Define la dirección de tus vectores de velocidad inicial como la dirección $+ x$. El momento inicial es entonces
$$\bold{\vec{p}}_i = m_1v_1\^{\bold{i}} + m_2v_2\^{\bold{i}}$$El momento final de los carros ahora vinculados es
$$\bold{\vec{p}}_f = (m_1 + m_2)v_f$$Igualando
$$(m_1 + m_2)v_f = m_1v_1\^{\bold{i}} + m_2v_2\^{\bold{i}}\\ \bold{\vec{v}}_f = \bigg(\frac{m_1v_1 + m_2v_2}{m_1 + m_2}\bigg)\^{\bold{i}}$$Sustituyendo los números dados:
$$\bold{\vec{v}}_f = \frac{(0.675 kg)(0.75 m/s)+(0.5 kg)(1.33 m/s)}{1.175 kg}\^{\bold{i}} = (0.997 m/s)\^{\bold{i}}$$Explicación
Los principios que se aplican aquí a dos carros de laboratorio se aplican de forma idéntica a todos los objetos de cualquier tipo o tamaño. Incluso para los fotones, los conceptos de momento y conservación del momento son aún crucialmente importantes incluso a esa escala (dado que no tienen masa, el momento de un fotón se define de manera muy diferente al momento de los objetos ordinarios. Aprenderás sobre esto cuando estudies la física cuántica).
 Comprueba tu aprendizaje 9.3
Comprueba tu aprendizaje 9.3
Ejemplo 9.7
Un rebote Superball
Se deja caer una superball de $0.25 kg$ de masa desde el reposo desde una altura de $h = 1.50 m$ sobre el suelo. Rebota sin pérdida de energía y vuelve a su altura inicial (Figura 9.17).
a. ¿Cuál es el cambio de momento del superball durante su rebote en el piso?
b. ¿Cuál fue el cambio de momento de la Tierra debido a que la pelota colisionó con el piso?
c. ¿Cuál fue el cambio de velocidad de la Tierra como resultado de esta colisión?
Este ejemplo muestra que debes tener cuidado al definir tu sistema.
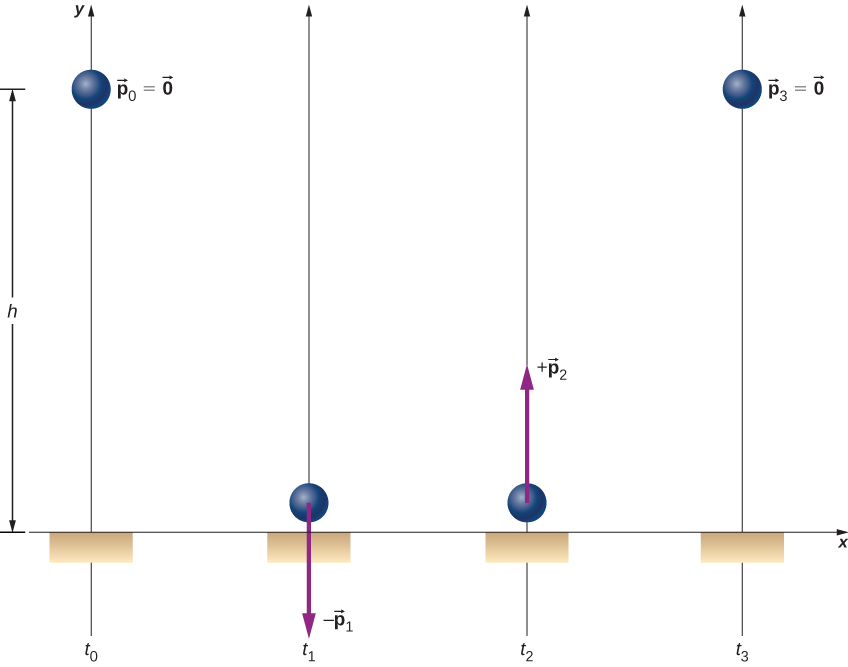
Estrategia
Como solo nos preguntan sobre el cambio de momento de la pelota, definimos que nuestro sistema es la pelota.
Pero esto claramente no es un sistema cerrado; la gravedad aplica una fuerza hacia abajo sobre la bola mientras está cayendo, y la fuerza normal del piso aplica una fuerza durante el rebote. Por lo tanto, no podemos usar la conservación del momento como una estrategia.
En cambio, simplemente determinamos el momento de la pelota justo antes de que colisione con el piso y justo después, y calculamos la diferencia. Tenemos la masa de la bola, por lo que necesitamos sus velocidades.
Solución
a. Como este es un problema unidimensional, usamos la forma escalar de las ecuaciones:
- $p_0$: la magnitud del momento de la pelota en el momento $t_0$, el momento en que fue lanzado; ya que se cayó del reposo, esto es cero.
- $p_1$: la magnitud del momento de la pelota en el tiempo $t_1$, el instante justo antes de que toque el piso.
- $p_2$: la magnitud del momento de la pelota en el tiempo $t_2$, justo después de que pierde el contacto con el piso después del rebote.
El cambio de momento de la pelota es
$$\Delta \bold{\vec{p}} = \bold{\vec{p}}_2 − \bold{\vec{p}}_1 = p_2\^{\bold{j}} − (−p_1\^{\bold{j}}) = (p_2 - p_1)\^{\bold{j}}$$La velocidad justo antes de que golpee el piso se puede determinar a partir de la conservación de la energía o la cinemática. Usamos cinemática aquí; deberías volver a resolverlo usando la conservación de la energía y confirmar que obtienes el mismo resultado.
Queremos la velocidad justo antes de que toque el suelo (en el momento $t_1$). Sabemos la velocidad inicial $v_0 = 0$ (en el tiempo $t_0$), la altura en que cae y su aceleración; no sabemos el tiempo de caída. Podríamos calcular eso, pero en cambio usamos
$$\bold{\vec{v}}_1 =−\^{\bold{j}}\sqrt{2gy} = −5.4 m/s\^{\bold{j}}$$Por lo tanto, la pelota tiene un momento de
$$\bold{\vec{p}}_1 = −(0.25 kg)(−5.4 m/s\^{\bold{j}}) = −(1.4 kg\cdot m/s)\^{\bold{j}}$$No tenemos una manera fácil de calcular el momento después del rebote. En cambio, razonamos desde la simetría de la situación.
Antes del rebote, la pelota comienza con velocidad cero y cae $1.50 m$ bajo la influencia de la gravedad, logrando cierta cantidad de momento justo antes de que toque el suelo. En el viaje de regreso (después del rebote), comienza con cierta cantidad de momento, sube los mismos 1,50 m que cayó y termina con velocidad cero. Por lo tanto, el movimiento después del rebote fue la imagen especular del movimiento antes del rebote. A partir de esta simetría, debe ser cierto que el momento de la bola después del rebote debe ser igual y opuesto a su momento antes del rebote (este es un argumento sutil pero crucial; asegúrate de entenderlo antes de continuar).
Por lo tanto
$$\bold{\vec{p}}_2 = -\bold{\vec{p}}_1 = +(1.4 kg\cdot m/s)\^{\bold{j}}$$Por lo tanto, el cambio de velocidad de la bola durante el rebote es
$$\begin{split} \Delta\bold{\vec{p}} &= \bold{\vec{p}}_2 - \bold{\vec{p}}_1\\ &= (1.4 kg\cdot m/s)\^{\bold{j}} − (−1.4kg\cdot m/s)\^{\bold{j}} = +(2.8kg\cdot m/s)\^{\bold{j}} \end{split}$$b. ¿Cuál fue el cambio de momento de la Tierra debido a que la pelota colisionó con el piso?
Tu respuesta instintiva bien pudo haber sido "cero"; la Tierra es demasiado grande para que esa pequeña bola la haya afectado "o posiblemente", más que cero, pero completamente insignificante.
Pero no, si redefinimos nuestro sistema para que sea Superball + Tierra, entonces este sistema está cerrado (despreciando los tirones gravitacionales del Sol, la Luna y los otros planetas del sistema solar), y por lo tanto, el cambio total de momento de este nuevo sistema debe ser cero. Por lo tanto, el cambio de momento de la Tierra es exactamente de la misma magnitud:
$$\Delta \bold{\vec{p}}_{tierra} = - 2.8kg\cdot m/s\^{\bold{j}}$$c. ¿Cuál fue el cambio de velocidad de la Tierra como resultado de esta colisión?
Aquí es donde tu sentimiento instintivo es probablemente correcto:
$$\begin{split} \Delta \bold{\vec{v}}_{tierra} &= \frac{\Delta\bold{\vec{p}}_{tierra}}{M_{tierra}}\\ &= \frac{2.8 kg\cdot m/s}{5.97 \times 10^{24} kg}\^{\bold{j}} = −(4.7 \times 10^{−25} m/s)\^{\bold{j}} \end{split}$$El cambio en la velocidad de la Tierra es completamente insignificante.
Explicación
Es importante darte cuenta que la respuesta a la parte (c) no es una velocidad; es un cambio de velocidad, que es algo muy diferente.
Sin embargo, para hacerte una idea de cuán pequeño es ese cambio de velocidad, supongamos que te estás moviendo con una velocidad de $4.7 \times 10^{-25} m/s$. A esta velocidad, te tomaría unos $7$ millones de años recorrer una distancia igual al diámetro de un átomo de hidrógeno.
 Comprueba tu aprendizaje 9.4
Comprueba tu aprendizaje 9.4
Ejemplo 9.8
Hockey sobre hielo 1
Dos discos de hockey de masa idéntica se encuentran en una pista horizontal de hockey sobre hielo. El disco rojo está inmóvil; el disco azul se mueve a $2.5 m/s$ hacia la izquierda (Figura 9.18) y choca con el disco rojo inmóvil. Los discos tienen una masa de $15 g$. Después de la colisión, el disco rojo se mueve a $2.5 m/s$, hacia la izquierda. ¿Cuál es la velocidad final del disco azul?
Estrategia
Nos dicen que tenemos dos objetos en colisión, nos dicen las masas y las velocidades iniciales, y una velocidad final; se nos pide las dos velocidades finales. La conservación del momento parece una buena estrategia. Define el sistema para que sea los dos discos; no hay fricción, entonces tenemos un sistema cerrado.
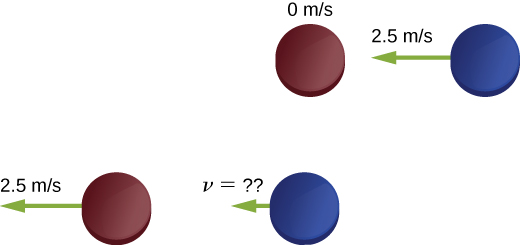
Antes de mirar la solución, ¿cuál crees que será la respuesta?
La velocidad final del disco azul será:
- cero
- $2,5 m/s$ a la izquierda
- $2,5 m/s$ a la derecha
- $1.25 m/s$ a la izquierda
- $1.25 m/s$ a la derecha
- algo más
Solución
Define la dirección $+ x$ a la derecha. La conservación del momento sería:
$$\bold{\vec{p}}_f = \bold{\vec{p}}_i$$Antes de la colisión, el momento del sistema es total y solo en el disco azul. Así,
$$mv_{Tf}\^{\bold{i}} + mv_{bf}\^{\bold{i}} = -mv_{b1}\^{\bold{i}}$$ $$v_{Tf}\^{\bold{i}} + v_{bf}\^{\bold{i}} = -v_{b1}\^{\bold{i}}$$(Recuerda que las masas de los discos son iguales.) Sustituyendo números:
$$−(2.5 m/s)\^{\bold{i}} + \bold{\vec{v}}_{bf} = −(2.5 m/s)\^{\bold{i}}$$ $$\bold{\vec{v}}_{bf} = \bold{\vec{0}}$$Explicación
Evidentemente, los dos discos simplemente intercambiaron momento. El disco azul transfirió todo su momento al disco rojo. De hecho, esto es lo que sucede en una colisión similar donde $m_1 = m_2$.
 Comprueba tu aprendizaje 9.5
Comprueba tu aprendizaje 9.5
Ejemplo 9.9
Aterrizaje del Philae
El 12 de noviembre de 2014, la Agencia Espacial Europea logró aterrizar una sonda llamada Philae en el Cometa 67P / Churyumov / Gerasimenko (Figura 9.19). Sin embargo, durante el aterrizaje, la sonda aterrizó tres veces, porque rebotó dos veces. Calculemos cuánto cambió la velocidad del cometa como resultado del primer rebote.

Definamos hacia arriba la dirección $+ y$, perpendicular a la superficie del cometa, y $y = 0$ en la superficie del cometa. Esto es lo que sabemos:
- La masa del Cometa 67P: $M_c = 1.0 \times 10 ^{13} kg$
- La aceleración debida a la gravedad del cometa: $\bold{\vec{a}} = - (5.0 \times 10^{-3} m/s^2\^{\bold{j}}$
- Masa del Philae: $M_p = 96 kg$
- Velocidad inicial de aterrizaje: $\bold{\vec{v}}_1 = - (1. m/s)\^{\bold{j}}$
- Velocidad inicial hacia arriba debido al primer rebote:
$\bold{\vec{v}}_2 = (0.3 8m/s)\^{\bold{j}}$ - Tiempo de impacto del aterrizaje: $\Delta t = 1.3 s$
Estrategia
Nos preguntan cuánto cambió la velocidad del cometa, pero no sabemos mucho sobre el cometa, más allá de su masa y la aceleración que causa su gravedad. Sin embargo, se nos dice que el módulo de aterrizaje del Philae colisiona con el cometa y rebota en él. Una colisión sugiere el momento como una estrategia para resolver este problema.
Si definimos un sistema que consta del Philae y el Cometa 67 / P, entonces no existe una fuerza externa neta en este sistema, y por lo tanto se conserva el momento de este sistema (despreciaremos la fuerza gravitatoria del sol). Por lo tanto, si calculamos el cambio de momento del módulo de aterrizaje, automáticamente tendremos el cambio de momento del cometa. Además, el cambio de velocidad del cometa está directamente relacionado con su cambio de momento como resultado de que el módulo de aterrizaje "colisiona" con él.
Solución
Deja que $\bold{\vec{p}}_1$ sea el momento del Philae en el momento justo antes de la toma de contacto, y $\bold{\vec{p}}_2$ sea su momento justo después del primer rebote. Entonces su momento justo antes del aterrizaje fue
$$\bold{\vec{p}}_1 = M_p\bold{\vec{v}}_1 = (96 kg)(−1.0 m/s\^{\bold{j}}) = −(96 kg\cdot m/s)\^{\bold{j}}$$y justo después fue
$$\bold{\vec{p}}_2 = M_p\bold{\vec{v}}_2 = (96 kg)(+0.38 m/s\^{\bold{j}}) = (36.5 kg\cdot m/s)\^{\bold{j}}$$Por lo tanto, el cambio de momento del módulo de aterrizaje durante el primer rebote es
$$\begin{split} \Delta \bold{\vec{p}} &= \bold{\vec{p}}_2 - \bold{\vec{p}}_1 = (36.5 kg\cdot m/s)\^{\bold{j}} − (−96.0 kg\cdot m/s\^{\bold{j}})\\ &= (133 kg\cdot m/s)\^{\bold{j}} \end{split}$$Observa cuán importante es incluir el signo negativo del momento inicial.
Ahora para el cometa. Como el momento del sistema debe conservarse, el momento del cometa cambió exactamente por el negativo de lo siguiente:
$$\Delta\bold{\vec{p}}_c = −\Delta \bold{\vec{p}} = −(133 kg\cdot m/s)\^{\bold{j}}$$Por lo tanto, su cambio de velocidad es
$$\Delta\bold{\vec{v}}_c = \frac{\Delta \bold{\vec{p}}_c}{M_c} = \frac{−(133 kg\cdot m/s)\^{\bold{j}}}{1.0 \times 10^{13} kg} = −(1.33 \times 10^{−11} m/s)\^{\bold{j}}$$Explicación
Este es un cambio muy pequeño en la velocidad, aproximadamente una milésima de una milmillonésima parte de un metro por segundo. Crucialmente, sin embargo, no es cero.
 Comprueba tu aprendizaje 9.6
Comprueba tu aprendizaje 9.6
Tipos de colisiones
Aunque el momento se conserva en todas las interacciones, no todas las interacciones (colisiones o explosiones) son las mismas. Las posibilidades incluyen:
- Un solo objeto puede explotar con múltiples objetos (uno a muchos).
- Múltiples objetos pueden colisionar y unirse, formando un solo objeto (muchos a uno).
- Múltiples objetos pueden colisionar y rebotar el uno del otro, permaneciendo como objetos múltiples (muchos a muchos). Si rebotan entre sí, pueden retroceder a la misma velocidad con la que se aproximaron antes de la colisión, o pueden moverse más lentamente.
Por lo tanto, es útil categorizar diferentes tipos de interacciones, según cómo se muevan los objetos que interactúan antes y después de la interacción.
Uno a muchos
La primera posibilidad es que un solo objeto se pueda dividir en dos o más piezas.
Estos pueden ser difíciles de analizar si el número de fragmentos después de la colisión es más de tres o cuatro; pero, no obstante, el momento total del sistema antes y después de la explosión es idéntico.
Ten en cuenta que si el objeto está inicialmente inmóvil, entonces el sistema (que es solo el objeto) no tiene momento ni energía cinética. Después de la explosión, el momento neto de todas las piezas del objeto debe sumar cero (ya que el momento de este sistema cerrado no puede cambiar). Sin embargo, el sistema tendrá una gran cantidad de energía cinética después de la explosión, aunque no tenía ninguno antes. Por lo tanto, vemos que, aunque el momento del sistema se conserva en una explosión, la energía cinética del sistema definitivamente no lo es, incrementa. En esta interacción, un objeto que se convierte en muchos, con un aumento de la energía cinética del sistema, se denomina explosión.
¿Dé dónde viene la energía? ¿La conservación de la energía aún se mantiene? Sí, alguna forma de energía potencial se convierte en energía cinética. En el caso de la pólvora que quema y empuja una bala, la energía potencial química se convierte en energía cinética de la bala y de la pistola. Para un arco y una flecha, es energía potencial elástica en la cuerda del arco.
Muchos a Uno
La segunda posibilidad es la inversa: que dos o más objetos colisionan entre sí y se unen, formando así (después de la colisión) un único objeto compuesto. La masa total de este objeto compuesto es la suma de las masas de los objetos originales, y el nuevo objeto individual se mueve con una velocidad dictada por la conservación del momento. Sin embargo, resulta que, aunque el momento total del sistema de objetos permanece constante, la energía cinética no lo hace, pero esta vez, la energía cinética disminuye.
Este tipo de colisión se llama inelástica. En el caso extremo, múltiples objetos colisionan, se adhieren y permanecen inmóviles después de la colisión. Como los objetos están completamente inmóviles después de la colisión, la energía cinética final también es cero, la pérdida de energía cinética es un máximo. Tal colisión se dice que es perfectamente inelástica.
Muchos a muchos
El caso extremo es si dos o más objetos se aproximan, colisionan y rebotan, alejándose el uno del otro a la misma velocidad relativa a la que se aproximan. En este caso, la energía cinética total del sistema se conserva. Tal interacción se llama elástica.
En cualquier interacción de un sistema cerrado de objetos, se conserva el momento total del sistema ($\bold{\vec{p}}_f = \bold{\vec{p}}_i$), pero la energía cinética puede no ser:
- Si $0 \lt K_f \lt K_i$, la colisión es inelástica.
- Si $K_f = 0$, la colisión es perfectamente inelástica.
- Si $K_f = K_i$, la colisión es elástica.
- Si $K_f \lt K:i$, la interacción es una explosión.
El objetivo de todo esto es que, al analizar una colisión o explosión, se pueda usar tanto el momento como la energía cinética.
En la siguiente simulación, diseñada por (Laurel Woods), puedes observar varias bolas de diferente masa y velocidad que colisionan conservando el momento total.
Un sistema cerrado siempre conserva el momento; también podría conservar energía cinética, pero muy a menudo no es así. Los problemas de energía-momento confinados a un avión (como los nuestros) generalmente tienen dos incógnitas. En general, este enfoque funciona bien:
- Definir un sistema cerrado.
- Escribe la expresión para la conservación del momento.
- Si se conserva la energía cinética, escribe la expresión para la conservación de la energía cinética; si no, escriba la expresión para el cambio de energía cinética.
- Ahora tiene dos ecuaciones y dos incógnitas, que puedes resolver por los métodos estándar.
Ejemplo 9.10
Formación de un Deuterón
Un protón (masa $1,67 \times 10^{-27} kg$) colisiona con un neutrón (con la misma masa que el protón) para formar una partícula llamada deuterón. ¿Cuál es la velocidad del deuterón si está formado por un protón que se mueve con una velocidad de $7.0 \times 10^6 m/s$ hacia la izquierda y un neutrón que se mueve con una velocidad de $4.0 \times 10^6 m/s$ hacia la derecha?

Estrategia
Define el sistema como las dos partículas. Esto es una colisión, así que primero debemos identificar de qué tipo.
Como se nos dice que las dos partículas forman una sola partícula después de la colisión, esto significa que la colisión es perfectamente inelástica. Por lo tanto, la energía cinética no se conserva, pero el momento sí. Por lo tanto, utilizamos la conservación de la energía para determinar la velocidad final del sistema.
Solución
Trata las dos partículas como si tuvieran masas idénticas $M$. Usa los subíndices $p, n$ y $d$ para protón, neutrón y deuterón, respectivamente. Este es un problema unidimensional, entonces tenemos
$$Mv_p - Mv_n = 2Mv_d$$Dividiendo por $M$
$$v_p - v_n = 2v_d\\ 7.0 \times 10^6 m/s − 4.0 \times 10^6 m/s = 2v_d\\ v_d = 1.5 \times 10^6 m/s$$La velocidad es entonces $\bold{\vec{r}}_d = (1.5 \times 10^6 m/s) \^{\bold{i}}$.
Explicación
Esto es esencialmente cómo funcionan los colisionadores de partículas como el Gran Colisionador de Hadrones: aceleran las partículas hasta velocidades muy altas (grandes momentos), pero en direcciones opuestas. Esto maximiza la creación de las llamadas "partículas hijas".
Ejemplo 9.11
Hockey sobre hielo 2
(Esta es una variación de un ejemplo anterior).
Dos discos de hockey sobre hielo de diferentes masas se encuentran en una pista horizontal de hockey. El disco rojo tiene una masa de $15$ gramos y está inmóvil; el disco azul tiene una masa de $12$ gramos y se mueve a 2.5 m/s hacia la izquierda. Choca con el disco rojo inmóvil (Figura 9.20). Si la colisión es perfectamente elástica, ¿cuáles son las velocidades finales de los dos discos?
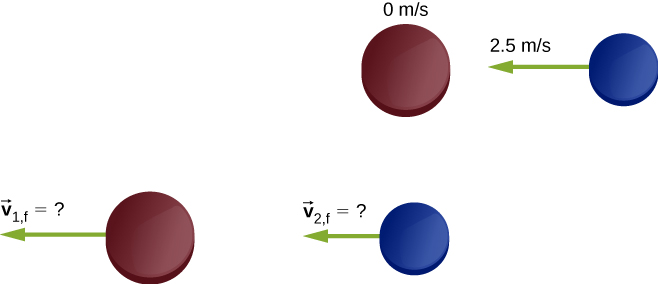
Estrategia
Se nos dice que tenemos dos objetos que colisionan, y nos dicen sus masas y velocidades iniciales, y una velocidad final; se nos pide las dos velocidades finales. La conservación del momento parece una buena estrategia; define el sistema como los dos discos.
No hay fricción, entonces tenemos un sistema cerrado. Tenemos dos incógnitas (las dos velocidades finales), pero solo una ecuación. El comentario acerca de que la colisión es perfectamente elástica es la clave; sugiere que la energía cinética también se conserva en esta colisión. Eso nos da nuestra segunda ecuación.
El momento inicial y la energía cinética inicial del sistema reside enteramente y solo en el segundo disco (el azul); la colisión transfiere algo de este momento y energía al primer disco.
Solución
Conservación del momento, en este caso,
$$p_i = p_f$$ $$m_2v_{2i} = m_1v_{1f} + m_2v_{2f}$$Conservación de energía cinética
$$K_i = K_f\\ \frac12 m_2v_{2i}^2 = \frac12 m_1v_{1f}^2 + \frac12 m_2v_{2f}^2$$Hay dos ecuaciones con dos incógnitas. El álgebra es tediosa pero no terriblemente difícil; Definitivamente deberías trabajarla. La solucion es
$$v_{1f} = \frac{(m_1 - m_2)v_{1i} + 2m_2v_{2i}}{m_1 + m_2}$$ $$v_{2f} = \frac{(m_2 - m_1)v_{1i} + 2m_1v_{1i}}{m_1 + m_2}$$Sustituyendo los datos obtenidos,
$$v_{1f} = 2.22 m/s\\ v_{2f} = -0.25 m/s$$Explicación
Ten en cuenta que después de la colisión, el disco azul se mueve hacia la derecha; su dirección de movimiento fue revertida. El disco rojo ahora se mueve hacia la izquierda.
 Comprueba tu aprendizaje 9.7
Comprueba tu aprendizaje 9.7
Ejemplo 9.12
Thor vs. Iron Man
La película de 2012 "The Avengers" tiene una escena en la que Iron Man y Thor luchan. Al comienzo de la pelea, Thor lanza su martillo a Iron Man, lo golpea y lo lanza ligeramente al aire y contra un árbol pequeño, que se rompe. Del video, Iron Man está parado cuando el martillo lo golpea. La distancia entre Thor e Iron Man es de aproximadamente $10 m$, y el martillo tarda aproximadamente $1 s$ en llegar a Iron Man luego de que Thor lo libera. El árbol está a unos $2 m$ detrás de Iron Man, que golpea en aproximadamente $0,75 s$.
También en el video, la trayectoria de Iron Man hacia el árbol está muy cerca de la horizontal. Suponiendo que la masa total de Iron Man es de $200 kg$:
a. Estima la masa del martillo de Thor
b. Calcula cuánta energía cinética se perdió en esta colisión
Estrategia
Después de la colisión, el martillo de Thor está en contacto con Iron Man durante todo el tiempo, por lo que esta es una colisión perfectamente inelástica. Por lo tanto, con la elección correcta de un sistema cerrado, esperamos que se conserve el momento, pero no la energía cinética. Usamos los datos dados para estimar el momento inicial, la energía cinética inicial y la energía cinética final. Debido a que este es un problema unidimensional, podemos ir directamente a la forma escalar de las ecuaciones.
a. Iniciamos con la conservación del momento. Para eso, necesitamos un sistema cerrado.
La elección aquí es el sistema (martillo + Iron Man), desde el momento de la colisión hasta el momento justo antes de que Iron Man y el martillo golpeen el árbol. Supongamos:
- $M_H$ = masa del martillo
- $M_I$ = masa de Iron Man
- $v_H$ = velocidad del martillo antes de golpear a Iron Man
- $v$ = velocidad combinada de Iron Man + el martillo después de la colisión
Nuevamente, la velocidad inicial de Iron Man fue cero. La conservación del momento nos dice:
$$M_Hv_H = (M_H + M_I)v$$Se nos pide que encontremos la masa del martillo, entonces tenemos
$$M_Hv_H = M_Hv + M_Iv\\ M_H(v_H - v)= M_Iv$$ $$M_H = \frac{M_Iv}{v_H - v}$$ $$M_H = \frac{(200 kg)(2 m/0.75 s)}{10 m/s − (2 m/0.75 s)} = 73 kg$$Teniendo en cuenta las incertidumbres en nuestras estimaciones, esto debe expresarse con solo una cifra significativa; por lo tanto, $M_H = 7 \times 10^1 kg$.
b. La energía cinética inicial del sistema, como el momento inicial, está en el martillo:
$$K_i = \frac12 M_Hv_H^2 = \frac12 (70 kg)(10 m/s)^2 = 3500 J<$$Después de la colisión:
$$K_f = \frac 12(M_H + M_I)v^2 = \frac12 (70 kg + 200 kg)(2.67 m/s)^2 = 960 J$$Por lo tanto, hubo una pérdida de $3500 J - 960 J = 2540 J$.
Explicación
De otras escenas en la película, Thor aparentemente puede controlar la velocidad del martillo con su mente.
Es posible, por lo tanto, que mentalmente haga que el martillo mantenga su velocidad inicial de $10 m/s$ mientras que Iron Man está siendo empujado hacia atrás en dirección al árbol. Si es así, esto representaría una fuerza externa en nuestro sistema, por lo que no se cerraría. Sin embargo, el control mental de Thor de su martillo está más allá del alcance de este libro.
Ejemplo 9.13
Analizando un accidente automovilístico
En un semáforo, un camión grande ($3000 kg$) colisiona con un automóvil pequeño inmóvil ($1200 kg$). El camión llega a una parada instantánea; el auto se desliza hacia adelante y se detiene después de $10$ metros.
El coeficiente de fricción medido entre los neumáticos del automóvil y la carretera fue de $0,62$. ¿Qué tan rápido se movió el camión en el momento del impacto?
Estrategia
Al principio, puede parecer que no tenemos suficiente información para resolver este problema. Aunque conocemos la velocidad inicial del automóvil, no conocemos la velocidad del camión (de hecho, eso es lo que se nos pide que encontremos), por lo que no conocemos el momento inicial del sistema.
Del mismo modo, sabemos la velocidad final del camión, pero no la velocidad del automóvil inmediatamente después del impacto. El hecho de que el automóvil eventualmente se deslizó a una velocidad de cero no ayuda con el momento final, ya que una fuerza de fricción externa causó eso. Tampoco podemos calcular un impulso, ya que no conocemos el tiempo de colisión, o la cantidad de tiempo que el automóvil se deslizó antes de detenerse. Una estrategia útil es imponer una restricción al análisis.
Supongamos que definimos un sistema que consiste solo en el camión y el automóvil. El momento de este sistema no se conserva debido a la fricción entre el automóvil y la carretera. Pero si pudiéramos encontrar la velocidad del automóvil al instante después del impacto, antes de que la fricción tuviera algún efecto medible en el automóvil, entonces podríamos considerar el momento del sistema para conservarlo, con esa restricción.
¿Podemos encontrar la velocidad final del auto? Sí. invoquemos el teorema del trabajo-energía.
Solución
Primero, define algunas variables. Supón:
- $M_c$ y $M_T$ como las masas del automóvil y camión, respectivamente
- $v_{Ti}$ y $v_{Tf}$ como las velocidades del camión antes y después de la colisión, respectivamente
- $v_{ci}$ y $v_{cf}$ como las velocidades del automóvil antes y después de la colisión, respectivamente
- $K_i$ y $K_f$ como las energías cinéticas del automóvil inmediatamente después de la colisión, y después de que el automóvil ha dejado de deslizarse (entonces $K_f = 0$).
- $d$ como la distancia que el automóvil se desliza después de la colisión antes de que finalmente se detenga.
Como realmente queremos la velocidad inicial del camión, y dado que el camión no forma parte del cálculo del teorema trabajo-energía, comencemos con la conservación del momento. Para el sistema de automóvil + camión, la conservación del momento dice
$$p_i = p_f\\ M_cv_{ci} + M_Tv_{Ti} = M_cv_{cf} + M_Tv_{Tf}$$Dado que la velocidad inicial del vehículo era cero, al igual que la velocidad final del camión, esto simplifica a
$$v_{Ti} = \frac{M_c}{M_T}v_{cf}$$Entonces ahora necesitamos la velocidad del auto inmediatamente después del impacto. Recuerda que
$$W = \Delta K$$donde,
$$\Delta K = K_f - K_i = 0 - \frac12 M_cv_{cf}^2$$También,
$$W = \bold{\vec{F}}\cdot \bold{\vec{d}} = Fdcos\theta$$El trabajo se realiza sobre la distancia que se desliza el automóvil, que hemos llamado d. Igualando:
La fricción es la fuerza del automóvil que hace el trabajo para detener el deslizamiento. Con un camino nivelado, la fuerza de fricción es
$$F = \mu_k M_cg.$$Como el ángulo entre las direcciones del vector de fuerza de fricción y el desplazamiento $d$ es $180°$, y $cos (180°) = - 1$, tenemos
$$−(\mu_k M_c g)d = -\frac12 M_cv_{cf}^2$$(Ten en cuenta que la masa del automóvil se divide, evidentemente, la masa del automóvil no importa).
Hallando la velocidad del automóvil inmediatamente después de la colisión
Sustituyendo los datos dados:
$$v_{cf} = \sqrt{2(0.62)(9.81 m/s^2)(10m)} = 11.0 m/s$$Ahora podemos calcular la velocidad inicial del camión:
$$v_{Ti} = \Big(\frac{1200 kg}{3000 kg}\Big)(11.0 m/s) = 4.4 m/s$$Explicación
Este es un ejemplo del tipo de análisis realizado por los investigadores de los principales accidentes automovilísticos.
Una gran cantidad de consecuencias legales y financieras dependen de un análisis y cálculo precisos del momento y la energía.
 Comprueba tu aprendizaje 9.8
Comprueba tu aprendizaje 9.8
Colisiones subatómicas y momentum
La conservación del momento es crucial para nuestra comprensión de las partículas atómicas y subatómicas, porque gran parte de lo que sabemos sobre estas partículas proviene de experimentos de colisión.
A principios del siglo XX, hubo un considerable interés y debate sobre la estructura del átomo. Se sabía que los átomos contienen dos tipos de partículas cargadas eléctricamente: electrones cargados negativamente y protones con carga positiva (Se sospechaba la existencia de una partícula eléctricamente neutra, pero no se confirmaría hasta 1932). La pregunta era, ¿cómo se organizaron estas partículas en el átomo? ¿Se distribuyeron uniformemente en todo el volumen del átomo (como propuso JJ Thomson), o dispuestos en las esquinas de los polígonos regulares (que era el modelo de Gilbert Lewis), o anillos de carga negativa que rodean el núcleo cargado positivamente, más bien como los anillos planetarios que rodean a Saturno (como lo sugirió Hantaro Nagaoka), o algo más?
El físico de Nueva Zelanda Ernest Rutherford (junto con el físico alemán Hans Geiger y el físico británico Ernest Marsden) realizaron el experimento crucial en 1909. Bombardearon una delgada lámina de oro con un rayo de alta energía (es decir, de alta velocidad) de partículas alfa (el núcleo de un átomo de helio).
Las partículas alfa colisionaron con los átomos de oro, y sus velocidades subsecuentes fueron detectadas y analizadas, utilizando la conservación del momento y la conservación de la energía.
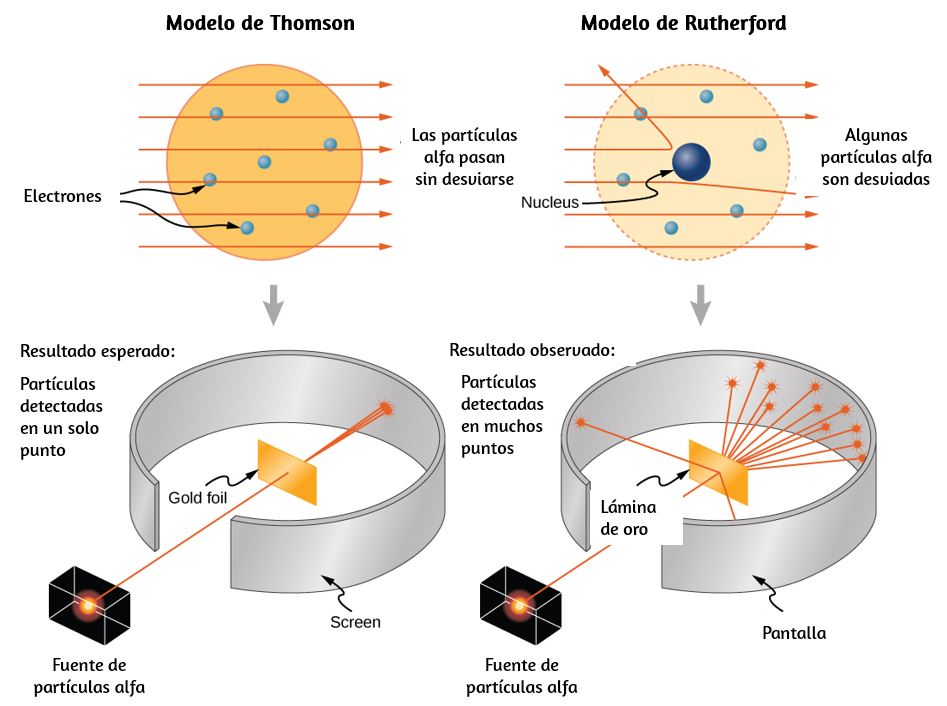
Si las cargas de los átomos de oro se distribuyen uniformemente (según Thomson), entonces las partículas alfa deberían colisionar con ellas y casi todas se desviarán en muchos ángulos, todas pequeñas; el modelo Nagaoka produciría un resultado similar.
Si los átomos se organizaran como polígonos regulares (Lewis), las partículas alfa se desviarían en un número relativamente pequeño de ángulos.
Lo que realmente sucedió es que casi ninguna de las partículas alfa se desvió. Aquellas que fueron desviadas en ángulos grandes, algunos cerca de $180\degree$, invirtieron la dirección por completo (Figura 9.21) . Ninguno de los modelos atómicos existentes podría explicar esto. Eventualmente, Rutherford desarrolló un modelo del átomo que estaba mucho más cerca de lo que ahora tenemos, una vez más, usando como punto de partida la conservación del momento y la energía.
En la siguiente escena interactiva, diseñada por Ionică Bizău, puedes observar los modelos de Thomson y de Rutherford. Desplaza la fuente de partículas, de tal forma que las partículas colisionen con el núcleo. La escena se presenta en dos idiomas, rumano y español.
Colisiones en múltiples dimensiones
Es mucho más común que las colisiones ocurran en dos dimensiones; es decir, el ángulo entre los vectores de velocidad iniciales no es cero ni $180°$. Veamos qué complicaciones surgen de esto.
La primera idea que necesitamos es que el momentum es un vector; como todos los vectores, se puede expresar como una suma de componentes perpendiculares (generalmente, aunque no siempre, un componente x y un componente y, y un componente z si es necesario). Por lo tanto, cuando escribimos la declaración de la conservación del momento para un problema, nuestros vectores de momento pueden ser, y usualmente serán, expresados en forma de componentes.
La segunda idea que necesitamos proviene del hecho de que el momento está relacionado con la fuerza:
$$\bold{\vec{F}} = \frac{d\bold{\vec{p}}}{dt}$$Expresando tanto la fuerza como el momento en forma de componentes,
$$F_x = \frac{dp_x}{dt}, \;\;F_y = \frac{dp_y}{dt}\;\;\, y \;\;\,F_z = \frac{dp_z}{dt}$$Recuerda, estas ecuaciones son simplemente la segunda ley de Newton, en forma de vector y en forma de componentes. Sabemos que la segunda ley de Newton es verdadera en cada dirección, independientemente de las demás.
la tercera ley de Newton) que la conservación del momento también es cierta en cada dirección de manera independiente.Estas dos ideas motivan la solución a problemas bidimensionales: escribimos la expresión para la conservación del momento dos veces: una en la dirección $x$ y otra en la dirección $y$.
Este procedimiento se muestra gráficamente en la figura 9.22.
Resolvemos cada una de estas dos ecuaciones de forma independiente para obtener los componentes x e y del vector de velocidad deseado:
$$v_{f,x} = \frac{m_1v_{1,i,x} + m_2v_{2,i,x}}{m}$$ $$v_{f,y} = \frac{m_1v_{1,i,y} + m_2v_{2,i,y}}{m}$$(Aquí, $m$ representa la masa total del sistema). Finalmente, combina estos componentes usando el teorema de Pitágoras,
$$v_f = |\bold{\vec{v}}_f| = \sqrt{v_{f,x}^2 + v_{f,y}^2}$$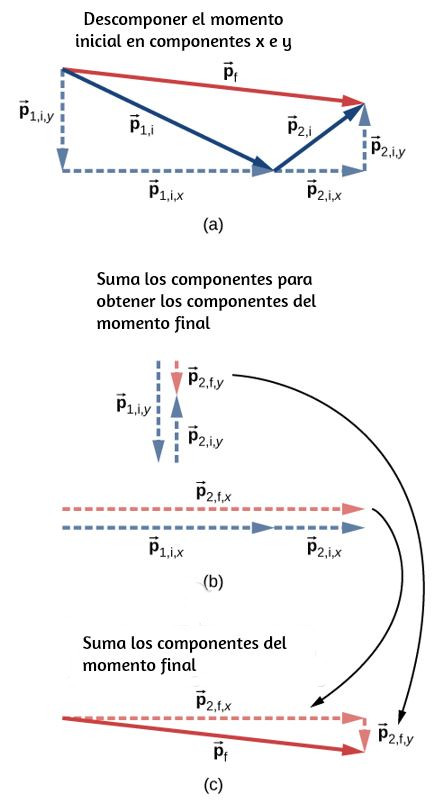
El método para resolver un problema bidimensional (o incluso tridimensional) de conservación del momento es generalmente el mismo que el método para resolver un problema unidimensional, excepto que debe conservar el momento en ambas (o las tres) dimensiones simultáneamente:
- Identifica un sistema cerrado.
- Escribe la ecuación que representa la conservación del momento en la dirección x y resuélvala para la cantidad deseada. Si estás calculando una cantidad vectorial (velocidad, generalmente), esto te dará el componente $x$ del vector.
- Escribe la ecuación que representa la conservación del momento en la dirección $y$, y resuelve. Esto te dará el componente $y$ de su cantidad vectorial.
- Suponiendo que estás calculando una cantidad vectorial, utiliza el teorema de Pitágoras para calcular su magnitud, utilizando los resultados de los pasos 3 y 4.
Ejemplo 9.14
Accidente de tránsito
Un pequeño automóvil de $1200 kg$ de masa que viaja hacia el este a $60 km/h$ colisiona en una intersección con un camión de $3.000 kg$ de masa, que viaja hacia el norte a $40 km/h$ (Figura 9.23).
Los dos vehículos están bloqueados. ¿Cuál es la velocidad de los restos de la catástrofe combinada?
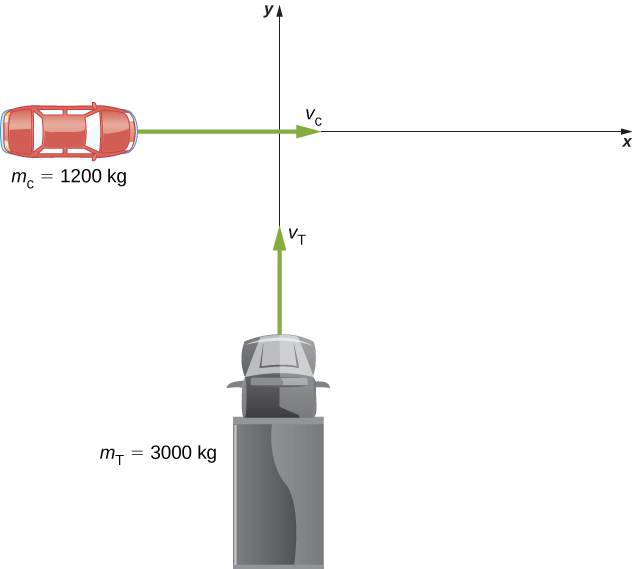
Estrategia
En primer lugar, necesitamos un sistema cerrado. El sistema natural para elegir es el (carro + camión), pero este sistema no está cerrado; la fricción de la carretera actúa en ambos vehículos.
Evitamos este problema restringiendo la pregunta a encontrar la velocidad en el instante justo después de la colisión, de modo que la fricción aún no haya tenido ningún efecto en el sistema. Con esa restricción, se conserva el impulso para este sistema.
Como hay dos direcciones involucradas, aplicamos la conservación del momento dos veces: una vez en la dirección $x$ y una vez en la dirección $y$.
Solución
Antes de la colisión, el momento total era
$$\bold{\vec{p}} = m_c\bold{\vec{v}}_c + m_Tv\bold{\vec{v}}_T$$Después de la colisión, los restos de la catástrofe tienen momento
$$\bold{\vec{p}} = (m_c + m_T)\bold{\vec{v}}_w$$Dado que el sistema está cerrado, el momento debe conservarse, por lo que tenemos
$$m_c\bold{\vec{v}}_c + m_T\bold{\vec{v}}_T = (m_c + m_T)\bold{\vec{v}}_w$$Tenemos que ser cuidadosos; los dos momentos iniciales no son paralelos. Debemos sumarlos vectorialmente (Figura 9.24).
Si definimos la dirección + x apuntando al este y la dirección + y para apuntando al norte, como en la figura, entonces,
$$\bold{\vec{p}}_c = p_c\^{\bold{i}} = m_cv_c\^{\bold{i}}\\ \bold{\vec{p}}_T = p_T\^{\bold{j}} = m_Tv_T\^{\bold{j}}$$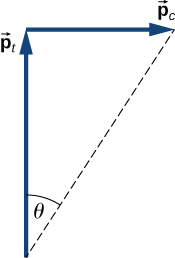
Por lo tanto, en la dirección $x$:
$$m_cv_c = (m_c + m_T)v_{w,x}$$ $$v_{w,x} = \Big(\frac{m_T}{m_c + m_T}\Big)v_T$$Aplicando el teorema de Pitágoras obtenemos
$$\begin{split} \big|\bold{\vec{v}}_w\big| &= \sqrt{\bigg[\Big(\frac{m_T}{m_c + m_T}\Big)v_c\bigg]^2 + \bigg[\Big(\frac{m_T}{m_c + m_T}\Big)v_T\bigg]^2}\\ &= \sqrt{\bigg[\Big(\frac{1200kg}{4200kg}\Big)(16.67m/s)\bigg]^2 + \bigg[\Big(\frac{3000kg}{4200kg}\Big)(11.1m/s)\bigg]^2}\\ &= \sqrt{(4.76m/s)^2 + (7.93m/s)^2}\\ &= 9.25m/s \approx 33.3 km/h \end{split}$$En cuanto a su dirección, usamos el ángulo que se muestra en la figura,
Este ángulo está al noreste, o $31\degree$ en el sentido contrario a las agujas del reloj desde la dirección $+ x$.
Explicación
Como cuestión práctica, los investigadores de accidentes generalmente trabajan en la "dirección opuesta"; miden la distancia de las marcas de deslizamiento en la carretera (lo que da la distancia de frenado) y utilizan el teorema del trabajo-energía junto con la conservación del momento para determinar las velocidades y las direcciones de los autos antes de la colisión. Vimos ese análisis en una sección anterior.
 Comprueba tu aprendizaje 9.9
Comprueba tu aprendizaje 9.9
Ejemplo 9.15
Explosión del tanque de buceo
Un tanque de buceo común es un cilindro de aluminio que pesa $31.7$ libras al vacío (Figura 9.25). Cuando está lleno de aire comprimido, la presión interna está entre $2500$ y $3000 psi$ (libras por pulgada cuadrada). Supongamos que ese tanque, que había estado inmóvil, de repente explota en tres pedazos.
La primera pieza, que pesa $10$ libras, se dispara horizontalmente a $235$ millas por hora; la segunda pieza ($7$ libras) se dispara a $172$ millas por hora, también en el plano horizontal, pero en un ángulo de $19\degree$ con respecto a la primera pieza. ¿Cuál es la masa y la velocidad inicial de la tercera pieza? (Haz todo el trabajo y expresa tu respuesta final en unidades del SI).
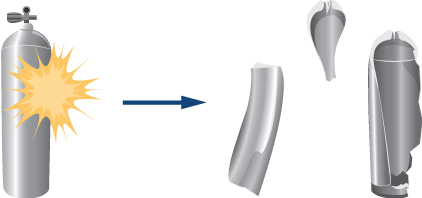
Estrategia
Para aplicar la conservación del momento, necesitamos un sistema cerrado. Si definimos el sistema como el tanque de buceo, este no es un sistema cerrado, ya que la gravedad es una fuerza externa. Sin embargo, el problema requiere la velocidad inicial de la tercera pieza, por lo que podemos despreciar el efecto de la gravedad y considerar el tanque como un sistema cerrado.
Ten en cuenta que, para este sistema, el vector de momento inicial es cero.
Elegimos un sistema de coordenadas donde todo el movimiento ocurre en el plano $xy$. Luego escribimos las ecuaciones para la conservación del momento en cada dirección, obteniendo así los componentes $x$ e $y$ del momento de la tercera pieza, de donde obtenemos su magnitud (a través del teorema de Pitágoras) y su dirección.
Finalmente, dividimos este momento por la masa de la tercera pieza que nos da la velocidad.
Solución
Primero, hagamos todas las conversiones a las unidades del SI:
$$31.7 lb \times (1kg/2.2 lb) \to 14.4 kg\\ 10 lb \to 4.5 kg\\ 235 (millas/horas) \times (1 hora/3600 s) \times (1609 m/millas)\\ = 105 m/s\\ 7 lb \to 3.2 kg\\ 172 millas/hora = 77 m/s\\ m_3 = 14.4 kg − (4.5 kg + 3.2 kg) = 6.7kg$$Ahora, aplica la conservación del momento en cada dirección.
Dirección $x$
$$p_{f,x} = p_{0,x}\\ p_{1,x} + p_{2,x} + p_{3,x} = 0\\ m_1v_{1,x} + m_2v_{2,x} + p_{3,x} = 0\\ p_{3,x} = -m_1v_{1,x} - m_2v_{2,x}$$Dirección $y$
$$p_{f,y} = p_{0,y}\\ p_{1,y} + p_{2,y} + p_{3,y} = 0\\ m_1v_{1,y} + m_2v_{2,y} + p_{3,y} = 0\\ p_{3,y} = -m_1v_{1,y} - m_2v_{2,y}$$Desde nuestro sistema de coordenadas elegido, escribimos los componentes $x$ así
$$\begin{split} p_{3,x} &= −m_1v_1 − m_2v_2cos\theta\\ &= −(14.5 kg)(105 m/s) − (4.5 kg)(77 m/s)cos(19\degree)\\ &= −1850 kg\cdot m/s \end{split}$$Para la dirección $y$, tenemos
$$\begin{split} p_{3,y} &= 0 − m_2v_2sen\theta\\ &= −(4.5 kg)(77 m/s)sen(19\degree)\\ &= −113 kg\cdot m/s \end{split}$$Esto te da la magnitud de $p_3$:
$$\begin{split} p_3 &= \sqrt{p_{3,x}^2 + p_{3,y}^2}\\ &= \sqrt{(−1850 kg\cdot m/s)^2 + (−113 kg\cdot m/s)^2}\\ &= 1854 kg\cdot m/s \end{split}$$La velocidad de la tercera pieza es por lo tanto
$$v_3 = \frac{p_3}{m_3} = \frac{1854 kg\cdot m/s}{6.7 kg} = 277 m/s$$La dirección de tu vector de velocidad es la misma que la dirección de tu vector de momento:
$$\phi = tan^{−1}\Big(\frac{p_{3,y}}{p_{3,x}}\Big) = tan^{−1}\Big(\frac{113 kg\cdot m/s}{1850 kg\cdot m/s}\Big) = 3.5\degree$$Como $\phi$ está debajo del eje $-x$, el ángulo real es $183.5\degree$ desde la dirección $+ x$.
Explicación
Las enormes velocidades aquí son típicas; un tanque explosivo de cualquier gas comprimido puede atravesar fácilmente la pared de una casa y causar lesiones importantes o la muerte. Afortunadamente, tales explosiones son extremadamente raras, sobre una base porcentual.
 Comprueba tu aprendizaje 9.10
Comprueba tu aprendizaje 9.10
Centro de masa
Hemos estado evitando un problema importante hasta ahora: cuando decimos que un objeto se mueve (más correctamente, acelera) de una manera que obedece a la segunda ley de Newton, hemos estado ignorando el hecho de que todos los objetos están realmente hechos de muchas partículas constituyentes. Un automóvil tiene un motor, volante, asientos, pasajeros; un balón de fútbol es cuero y caucho que rodea el aire; un ladrillo está hecho de átomos.
Hay muchos tipos diferentes de partículas, y generalmente no se distribuyen uniformemente en el objeto. ¿Cómo incluimos estos hechos en nuestros cálculos?
Entonces, también, un objeto extendido puede cambiar de forma a medida que se mueve, como un globo de agua o un gato cayendo (Figura 9.26). Esto implica que las partículas constituyentes están aplicando fuerzas internas entre sí, además de la fuerza externa que actúa sobre el objeto como un todo. Queremos ser capaces de manejar esto, también.
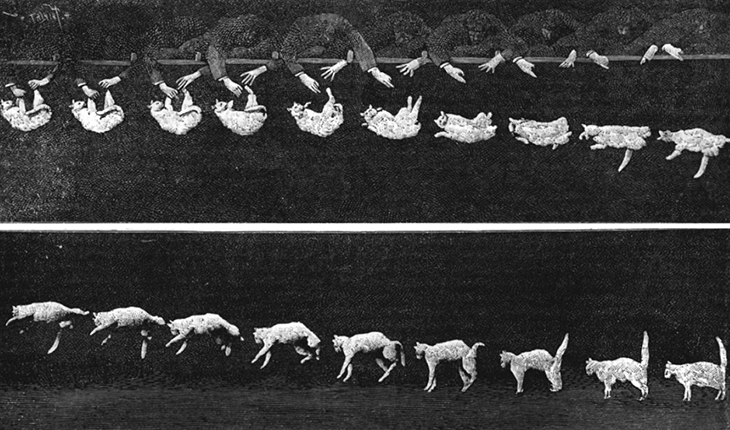
El problema que tenemos ante nosotros, entonces, es determinar qué parte de un objeto extendido obedece a la segunda ley de Newton cuando se aplica una fuerza externa y cómo el movimiento del objeto como un todo se ve afectado por las fuerzas internas y externas.
Ten cuidado: para tratar esta nueva situación correctamente, debemos ser rigurosos y completamente generales.
No haremos suposiciones sobre la naturaleza del objeto, o de sus partículas constituyentes, o las fuerzas internas o externas. Por lo tanto, los argumentos serán complejos.
Fuerzas Internas y Externas
Supongamos que tenemos un objeto extendido de masa $M$, formado por $N$ partículas que interactúan. Etiquetemos sus masas como $m_j$, donde $j = 1,2,3, \dots , N%. Ten en cuenta que
Si aplicamos una fuerza externa neta $\bold{\vec{F}}$ sobre el objeto, cada partícula experimenta alguna "parte" o alguna fracción de esa fuerza externa. Hagamos:
$\bold{\vec{f}}_j^{ext}$: la fracción de la fuerza externa que experimenta la j-ésima partícula.Ten en cuenta que estas fracciones de la fuerza total no son necesariamente iguales; de hecho, prácticamente nunca lo son (pueden serlo, pero generalmente no lo son). En general, por lo tanto,
$$\bold{\vec{f}}_1^{ext} \ne \bold{\vec{f}}_2^{ext} \ne \bold{\vec{f}}_N^{ext}$$Luego, asumimos que cada una de las partículas que componen nuestro objeto puede interactuar (aplicar fuerzas sobre) con otra partícula del objeto. No trataremos de adivinar qué tipo de fuerzas son; pero como estas fuerzas son el resultado de partículas del objeto
que actúa sobre otras partículas del mismo objeto, nos referimos a ellas como fuerzas internas $\bold{\vec{f}}_j^{int}$, así:
$\bold{\vec{f}}_j^{int}$: la fuerza interna neta que experimenta la j-ésima partícula de todas las otras partículas que componen el objeto.
Ahora, la fuerza neta, interna más externa, en la j-ésima partícula es la suma vectorial:
donde, de nuevo, esto es para todas las $N$ partículas; $j = 1,2,3, \dots , N$.
Como resultado de esta fuerza fraccionaria, el momento de cada partícula cambia:
La fuerza neta $\bold{\vec{F}}$ en el objeto es la suma vectorial de estas fuerzas:
Esta fuerza neta cambia el momento del objeto como un todo, y el cambio neto de momento del objeto debe ser la suma vectorial de todos los cambios individuales de momento de todas las partículas:
Combinando las ecuaciones 9.22 y 9.23, obtenemos.
Ahora pensemos en estas sumas. Primero considera el término de las fuerzas internas; recuerde que cada $\bold{\vec{f}}_j^{int}$ es la fuerza sobre la j-ésima partícula de las otras partículas en el objeto. Pero según la tercera ley de Newton, para cada una de estas fuerzas, debe haber otra fuerza que tenga la misma magnitud, pero el signo opuesto. Estas fuerzas no se cancelan; sin embargo, eso no es lo que estamos haciendo en la sumatoria. Más bien, simplemente estamos sumando matemáticamente todos los vectores de fuerzas internas. Es decir, en general, las fuerzas internas para cualquier parte individual del objeto no se cancelarán, pero cuando se sumen todas las fuerzas internas, deben cancelarse. Se sigue, por lo tanto, que la suma de todas las fuerzas internas debe ser cero:
$$\sum_{j=1}^N \bold{\vec{f}}_j^{int} = 0$$(Este argumento es sutil, pero crucial, tómate el tiempo suficiente para comprenderlo por completo).
Para las fuerzas externas, esta suma es simplemente la fuerza externa total que se aplicó a todo el objeto:
$$\sum_{j=1}^N \bold{\vec{f}}_j^{ext} = \bold{\vec{f}}^{ext}$$Como resultado,
Este es un resultado importante. La ecuación 9.25 nos dice que el cambio total de momento de todo el objeto (todas las N partículas) se debe solo a las fuerzas externas; las fuerzas internas no cambian el momento del objeto como un todo. Es por eso que no puede levantarse en el aire parándose en una canasta y tirando de las asas: para el sistema de tu canasta, tu fuerza de tracción hacia arriba es una fuerza interna.
Fuerza y momento
Recuerda que nuestro objetivo real es determinar la ecuación de movimiento para todo el objeto (todo el sistema de partículas). Para ese fin, definamos:
$\bold{\vec{p}}_{CM}$: el momento total del sistema de N partículas (el motivo del subíndice se aclarará en breve)
Entonces tenemos
$$\bold{\vec{p}}_{CM} = \sum_{j=1}^N\bold{\vec{p}}_j$$y por lo tanto, la ecuación 9.25 se puede escribir simplemente como
Como este cambio de momento es causado solo por la fuerza externa neta, hemos descartado el subíndice "ext".
Esta es la segunda ley de Newton, pero ahora para todo el objeto extendido. Si esto te parece un poco anticlimático, recuerda lo que se esconde dentro de él: $\bold{\vec{p}}_{CM}$ es la suma vectorial del momento (en principio) de cientos de miles de billones de billones de partículas ($6.02 \times 10^{23}$), todo causado por una simple fuerza externa: una fuerza que puedes calcular.
Centro de masa
Nuestra siguiente tarea es determinar qué parte del objeto extendido, si lo hay, obedece a la Ecuación 9.26.
Es tentador dar el siguiente paso; ¿la siguiente ecuación significa algo?
Si significa algo (¿aceleración de qué, exactamente?), entonces podríamos escribir
$$M\bold{\vec{a}} = \frac{d\bold{\vec{p}}_CM}{dt}$$y por lo tanto
$$M\bold{\vec{a}} = \sum_{j=1}^N \frac{d\bold{\vec{p}}_j}{dt} = \frac{d}{dt} \sum_{j=1}^N\bold{\vec{p}}_j$$que sigue porque la derivada de una suma es igual a la suma de las derivadas.
Ahora, $\bold{\vec{p}}_j$ es el momento de la j-ésima partícula. Definiendo las posiciones de las partículas constituyentes (en relación con algún sistema de coordenadas) como $\bold{\vec{r}}_j = (x_j, y_j, z_j)$, tenemos así
$$\bold{\vec{p}}_j = m_j\bold{\vec{v}}_j = m_j\frac{d\bold{\vec{r}}_j} {dt}$$Sustituyendo, obtenemos
$$M\bold{\vec{a}} = \frac{d}{dt}\sum_{j=1}^N m_j \frac{d\bold{\vec{r}}_j}{dt}$$ $$M\bold{\vec{a}} = \frac{d^2}{dt^2}\sum_{j=1}^N m_j\bold{\vec{r}}_j$$Diviendo por M:
Por lo tanto, el punto en el objeto que rastrea la trayectoria impuesta por la fuerza aplicada en la Ecuación 9.27 está dentro del paréntesis en la Ecuación 9.28.
Al observar este cálculo, nota que (dentro de los paréntesis) estamos calculando el producto de la masa de cada partícula con su posición, sumándolos todos hasta $N$, y dividiendo esta suma por la masa total de partículas. Esto es una reminiscencia de un promedio; inspirado por esto, lo interpretaremos (vagamente) como la posición promedio ponderada de la masa del objeto extendido. En realidad se llama el centro de masa del objeto. Observa que la posición del centro de masa tiene unidades de metros; eso sugiere una definición:
Entonces, el punto que obedece a la ecuación 9.26 (y por lo tanto también a la ecuación 9.27) es el centro de masa del objeto, que está ubicado en el vector de posición $\bold{\vec{r}}_{CM}$.
Puedes sorprenderte saber que no tiene que haber ninguna masa real en el centro de masa de un objeto.
Por ejemplo, una esfera de acero hueco con un vacío en su interior es esféricamente simétrica (lo que significa que su masa está distribuida uniformemente alrededor del centro de la esfera), toda la masa de la esfera está afuera en su superficie, sin masa adentro. Pero se puede demostrar que el centro de masa de la esfera está en su centro geométrico, lo que parece razonable. Por lo tanto, no hay masa en la posición del centro de masa de la esfera (otro ejemplo es una donut). El procedimiento para encontrar el centro de masa se ilustra en la Figura 9.27.
Dado que $\bold{\vec{r}}_j = x_j\^{\bold{i}} + y_j\^{\bold{j}} + z_j\^{\bold{k}}$, se deduce que:
y por lo tanto
$$\bold{\vec{r}}_{CM} = \bold{\vec{r}}_{CM,x}\^{\bold{i}} + \bold{\vec{r}}_{CM,y}\^{\bold{j}} + \bold{\vec{r}}_{CM,z}\^{\bold{k}}$$ $$r_{CM} = |\bold{\vec{r}}_{CM}| = \sqrt{r_{CM,x}^2 + r_{CM,y}^2 + r_{CM,z}^2}$$Por lo tanto, puedes calcular los componentes del vector del centro de masa individualmente.
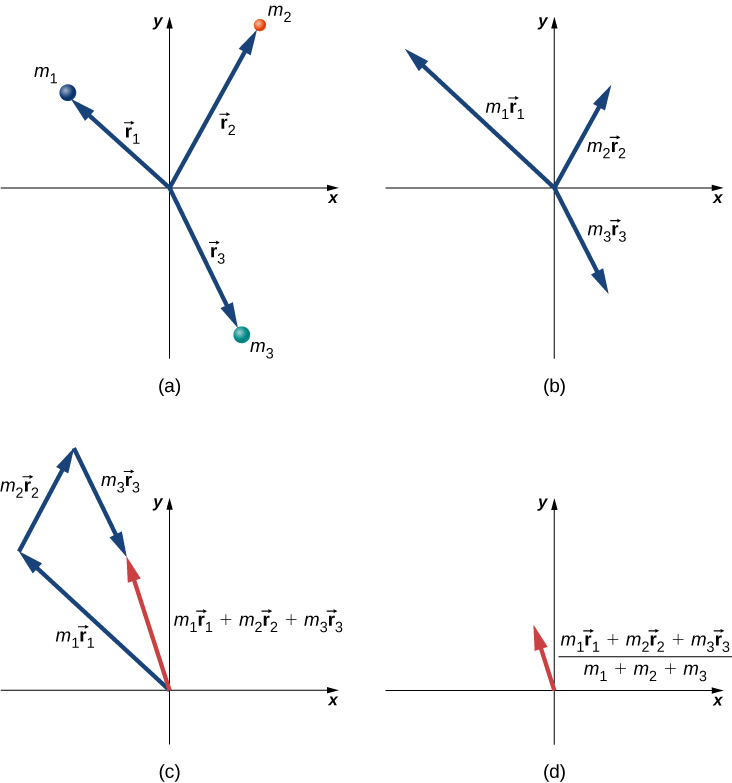
Finalmente, para completar la cinemática, la velocidad instantánea del centro de masa se calcula exactamente como se podría sospechar:
y esta, al igual que la posición, tiene componentes $x,y$ y $z$. Para calcular el centro de masa en situaciones reales, recomendamos el siguiente procedimiento:
El centro de masa de un objeto es un vector de posición. Por lo tanto, para calcularlo, sigue estos pasos:
- Define tu sistema de coordenadas. Típicamente, el origen se coloca en la ubicación de una de las partículas. Esto no es obligatorio, sin embargo.
- Determina las coordenadas $x, y, z$ de cada partícula que compone el objeto.
- Determina la masa de cada partícula y súmalas para obtener la masa total del objeto. Ten en cuenta que la masa del objeto en el origen debe incluirse en la masa total.
- Calcula las componentes $x, y$, y $z$ del vector del centro de masa, usando las ecuaciones 9.30, 9.31 y 9.32.
- Si es necesario, usa el teorema de Pitágoras para determinar su magnitud.
Aquí hay dos ejemplos que te darán una idea de lo que es el centro de masa.
Ejemplo 9.16
Centro de masa del sistema Tierra-Luna
Determina qué tan lejos está el centro de masa del sistema Tierra-Luna del centro de la Tierra. Compara esta distancia con el radio de la Tierra y comenta el resultado. Ignora los otros objetos en el sistema solar.
Estrategia
Obtenemos las masas y la distancia de separación de la Tierra y la Luna (puedes consultarlo en la red), imponemos un sistema de coordenadas y usamos la Ecuación 9.29 con solo $N = 2$ objetos. Usamos un subíndice "$e$" para referirnos a la Tierra, y un subíndice "$m$" para referirnos a la luna.
Solución
Define el origen del sistema de coordenadas como el centro de la Tierra. Entonces, con solo dos objetos, la Ecuación 9.29 se convierte en
$$R = \frac{m_er_e + m_mr_m}{m_e + m_m}$$Consultando en la red: $m_e = 5.97 \times 10^{24} kg,\;\; m_m = 7.36 \times 10^{22} kg\;\; y\;\; r_m = 3.82 \times 10^5 m$
Definimos el centro de la Tierra como el origen, por lo que $r_e = 0 m$. Reemplazando en la ecuación para $R$, obtenemos:
$$\begin{split} R &= \frac{(5.97 \times 10^{24} kg)(0 m) + (7.36 \times 10^{22} kg)(3.82 \times 10^8 m)}{5.98 \times 10^{24} kg + 7.36 \times 10^{22} kg}\\ &= 4.64 \times 10^6 m \end{split}$$Explicación
El radio de la Tierra es $6.37 \times 10^6 m$, por lo que el centro de masa del sistema Tierra-Luna es $(6.37 - 4.64) \times 10^6 m = 1.73 \times 10^6 m = 1730 km$ (aproximadamente $1080$ millas) debajo de la superficie de la Tierra. La ubicación del centro de masa se muestra en la siguiente figura (no está a escala).
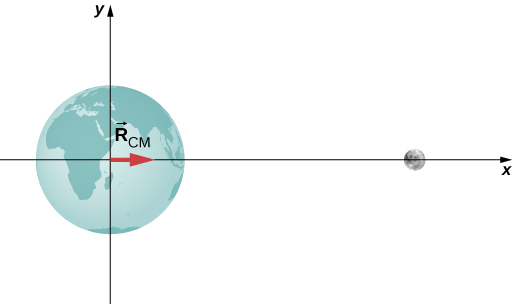
 Comprueba tu aprendizaje 9.11
Comprueba tu aprendizaje 9.11
Ejemplo 9.17
Centro de masa de un cristal de sal
La figura 9.28 muestra un solo cristal de sal de mesa ordinaria de cloruro de sodio. Los iones de sodio y cloruro forman una sola unidad, $NaCl$.
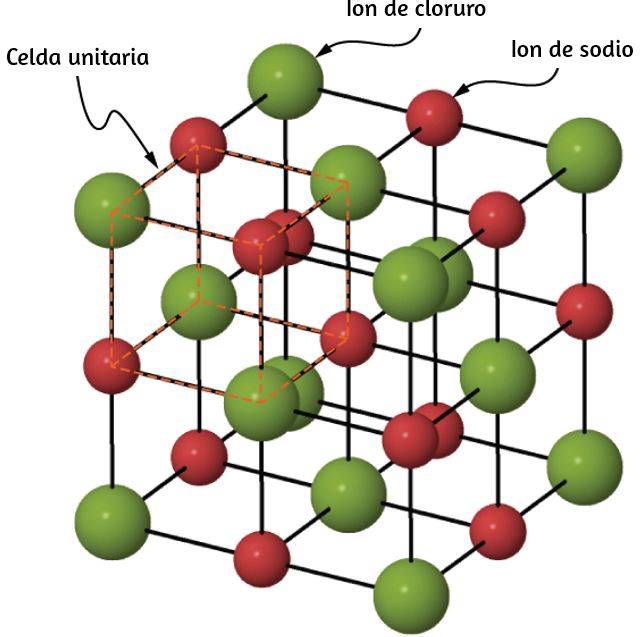
Cuando varias unidades de $NaCl$ se agrupan, forman una red cúbica. El cubo más pequeño posible (llamado celda unitaria) consta de cuatro iones de sodio y cuatro iones de cloruro, alternando. La longitud de un borde de este cubo (es decir, la longitud del enlace) es de $2,36 \times 10^{-10} m$. Encuentra la ubicación del centro de masa de la celda unitaria. Especifícalo por sus coordenadas ($r_{CM,x}, r_{CM,y}, r_{CM,z}$) o por $r_{CM}$ y dos ángulos.
Estrategia
Podemos buscar todas las masas de iones. Si imponemos un sistema de coordenadas en la celda unidad, esto nos dará las posiciones de los iones. Entonces podemos aplicar las ecuaciones 9.30, 9.31 y 9.32 (junto con el teorema de Pitágoras).
Solución
Define el origen para que esté en la ubicación del ion cloruro en la parte inferior izquierda de la celda unitaria. La figura 9.29 muestra el sistema de coordenadas.
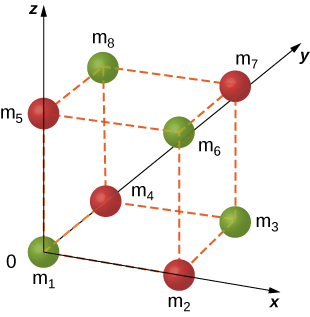
Hay ocho iones en este cristal, entonces $N = 8$:
$$\bold{\vec{r}}_{CM} = \frac{1}{M} \sum_{j=1}^8 m_j\bold{\vec{r}}_j$$La masa de cada uno de los iones cloruro es
$$35.453u \times \frac{1.660 \times 10^{−27} kg}{u} = 5.885 \times 10^{−26} kg$$entonces tenemos
$$m_1 = m_2 = m_6 = m_8 = 5.885 \times 10^{−26} kg$$Para los iones de sodio,
$$m_2 = m_4 = m_5 = m_7 = 3.816 \times 10^{−26} kg$$La masa total de la celda unitaria es por lo tanto
$$M = (4)(5.885 \times 10^{−26} kg)+(4)(3.816 \times 10^{−26} kg) = 3.880 \times 10^{−25} kg$$Desde la geometría, las ubicaciones son
$\bold{\vec{r}}_1 = 0\\ \bold{\vec{r}}_2 =( 2.36 \times 10^{−10} m)\^{\bold{i}}\\ \bold{\vec{r}}_3 = r_{3x}\^{\bold{i}} + r_{3y}\^{\bold{j}} = (2.36 \times 10^{−10} m)\^{\bold{i}} + (2.36 \times 10^{−10} m)\^{\bold{j}}\\ \bold{\vec{r}}_4 = (2.36 \times 10^{−10} m)\^{\bold{j}}\\ \bold{\vec{r}}_5 = (2.36 \times 10^{−10} m)\^{\bold{k}}\\ \bold{\vec{r}}_6 = r_{6x}\^{\bold{i}} + r_{6z}\^{\bold{k}} = (2.36 \times 10^{−10} m)\^{\bold{i}} + (2.36 \times 10^{−10} m)\^{\bold{k}}$
$\bold{\vec{r}}_7 = r_{7x}\^{\bold{i}} + r_{7y}\^{\bold{j}} + r_{7z}\^{\bold{k}} = (2.36 \times 10^{−10} m)\^{\bold{i}} + (2.36 \times 10^{−10} m)\^{\bold{j}} + (2.36 \times 10^{−10} m)\^{\bold{k}}\\ \bold{\vec{r}}_8 = r_{8y}\^{\bold{j}} + r_{8z}\^{\bold{k}} = (2.36 \times 10^{−10} m)\^{\bold{j}} + (2.36 \times 10^{−10} m)\^{\bold{k}}$.
Sustituyendo:
$$\begin{split} |\bold{\vec{r}}_{CM,x}| &= \sqrt{r_{CM,x}^2 + r_{CM,y}^2 + r_{CM,z}^2} = \frac{1}{M} \sum_{j=1}^8 m_j(r_x)_j\\ &= \frac{1}{M}(m_1r_{1x} + m_2r_{2x} + m_3r_{3x} + m_4r_{4x} + m_5r_{5x}\\ & \;\;\;\;\;+ m_6r_{6x} + m_7r_{7x} + m_8r_{8x})\\ &= \frac{1}{3.8804\times 10^{−25} kg} [(5.885 \times 10^{−26} kg)(0m) \\ & \;\;\;\;\;+ (3.816 \times 10^{−26}kg)(2.36 \times 10^{−10}m)\\ &= + (5.885 \times 10^{−26} kg)(2.36 \times 10^{−10} m)\\ &= + (3.816 \times 10^{−26} kg)(2.36 \times 10^{−10} m) + 0 + 0\\ &= + (3.816 \times 10^{−26} kg)(2.36 \times 10^{−10} m) + 0]\\ &= 1.18 \times 10^{−10} m \end{split}$$Cálculos similares se aplican para $r_{CM,y} = r_{CM,z} = 1.18 \times 10^{−10} m$ (se podría argumentar que esto debe ser cierto, por simetría, pero es una buena idea verificarlo).
Explicación
Aunque este es un gran ejercicio para determinar el centro de masa dado un ion de cloruro en el origen, de hecho, el origen podría elegirse en cualquier ubicación.
Por lo tanto, no hay una aplicación significativa del centro de masa de una celda unitaria más allá de un ejercicio.
 Comprueba tu aprendizaje 9.12
Comprueba tu aprendizaje 9.12
Dos conceptos cruciales provienen de estos ejemplos:
- Como con todos los problemas, debes definir tu sistema de coordenadas y origen. Para los cálculos del centro de masa, a menudo tiene sentido elegir que su origen se encuentre en una de las masas de tu sistema. Esa elección define automáticamente tu distancia en la Ecuación 9.29 como cero. Sin embargo, aún debes incluir la masa del objeto en su origen en tu cálculo de $M$, en la ecuación de masa total 9.19. En el ejemplo del sistema Tierra-Luna, esto significa incluir la masa de la Tierra. Si no lo hubieras hecho, hubieras terminado con el centro de masa del sistema en el centro de la luna, lo cual es claramente incorrecto.
- En el segundo ejemplo (el cristal de sal), observa que no hay masa en absoluto en la ubicación del centro de masa. Este es un ejemplo de lo que dijimos anteriormente, que no tiene que haber ninguna masa real en el centro de masa de un objeto.
Centro de masa de objetos continuos
Si el objeto en cuestión tiene su masa distribuida uniformemente en el espacio, en lugar de una colección de partículas discretas, entonces $m_j \to dm$, y la suma se convierte en una integral:
En este contexto, $r$ es una dimensión característica del objeto (el radio de una esfera, la longitud de una barra larga). Para generar un integrando que realmente pueda calcularse, necesitas expresar el elemento de masa diferencial dm como una función de la densidad de masa del objeto continuo, y la dimensión $r$. Un ejemplo aclarará esto.
Ejemplo 9.18
$CM$ de un aro fino uniforme
Encuentra el centro de masa de un aro (o anillo) delgado y uniforme de masa $M$ y radio $r$.
Estrategia
Primero, la simetría del aro sugiere que el centro de masa debe estar en su centro geométrico. Si definimos nuestro sistema de coordenadas de modo que el origen esté ubicado en el centro del aro, la integral debería evaluarse en cero.
Reemplazamos dm por una expresión que involucra la densidad del aro y el radio del aro.
Entonces tenemos una expresión que realmente podemos integrar.
Dado que el aro se describe como "delgado", lo tratamos como un objeto unidimensional, despreciando el grosor del aro. Por lo tanto, su densidad se expresa como la cantidad de kilogramos de material por metro. Tal densidad se llama densidad de masa lineal, y se le da el símbolo $\lambda$; esta es la letra griega "lambda", que es el equivalente de la letra inglesa "l" (para "lineal").
Como el aro se describe como uniforme, esto significa que la densidad de masa lineal $\lambda$ es constante. Por lo tanto, para obtener nuestra expresión para el elemento de masa diferencial dm, multiplicamos $\lambda$ por una longitud diferencial del aro, sustituimos e integramos (con los límites apropiados para la integral definida).
Solución
Primero, define nuestro sistema de coordenadas y las variables relevantes (Figura 9.30).
El centro de masa se calcula con la ecuación 9.34:
$$\bold{\vec{r}}_{CM} = \frac{1}{M}\int_a^b \bold{\vec{r}} dm$$Tenemos que determinar los límites de la integración $a$ y $b$. Expresar $\bold{\vec{r}}$ en forma de componentes
$$\bold{\vec{r}}_{CM} = \frac{1}{M}\int_a^b [(rcos\theta)\^{\bold{i}} + (rsen\theta)\^{\bold{j}}]dm$$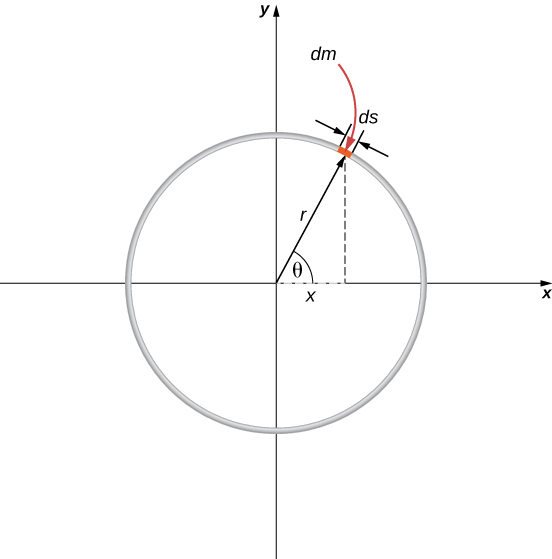
En el diagrama, resaltamos una pieza del aro que tiene una longitud diferencial ds; por lo tanto, tiene una masa diferencial $dm = \lambda ds$. Sustituyendo:
$$\bold{\vec{r}}_{CM} = \frac{1}{M}\int_a^b [(rcos\theta)\^{\bold{i}} + (rsen\theta)\^{\bold{j}}]\lambda ds$$Sin embargo, la longitud del arco ds subtiende un ángulo diferencial dθ, por lo que tenemos
$$ds = rd\theta$$y por lo tanto
$$\bold{\vec{r}}_{CM} = \frac{1}{M}\int_a^b [(rcos\theta)\^{\bold{i}} + (rsen\theta)\^{\bold{j}}]\lambda rd\theta$$Un paso más: dado que $\lambda$ es la densidad de masa lineal, se calcula dividiendo la masa total por la longitud del aro:
$$\lambda = \frac{M}{2\pi r}$$Obteniendo
$$\begin{split} \bold{\vec{r}}_{CM} &= \frac{1}{M}\int_a^b [(rcos\theta)\^{\bold{i}} + (rsen\theta)\^{\bold{j}}]\bigg(\frac{M}{2\pi r}\bigg) rd\theta\\ &= \frac{1}{2\pi}\int_a^b [(rcos\theta)\^{\bold{i}} + (rsen\theta)\^{\bold{j}}]d\theta \end{split}$$Observa que la variable de integración ahora es el ángulo $\theta$.
Esto nos dice que los límites de integración (alrededor del aro circular) son $\theta = 0$ a $\theta = 2\pi$, entonces $a = 0$ y $b = 2\pi$. Además, para mayor comodidad, separamos la integral en los componentes $x$ e $y$ de $\bold{\vec{r}}_{CM}$. La expresión integral final es
como se esperaba.
Centro de Masa y Conservación del Momento
¿Cómo se conecta todo esto con la conservación del momento?
Supongamos que tiene $N$ objetos con masas $m_1, m_2, m_3, \cdots m_N$ y velocidades iniciales $\bold{\vec{v}}_1, \bold{\vec{v}}_2, \bold{\vec{v}}_3, \cdots, \bold{\vec{v}}_N$. El centro de masa de los objetos es
$$\bold{\vec{r}}_{CM} = \frac{1}{M}\sum_{j=1}^N m_j\bold{\vec{r}}_j$$Su velocidad es
y así el momento inicial del centro de masa es
$$\Big[M\frac{d\bold{\vec{r}}_{CM}}{dt}\Big]_i = \sum_{j=1}^N m_j\frac{d\bold{\vec{r}}_{j,i}}{dt}$$Después de que estas masas se muevan e interactúen entre sí, el momento del centro de masa es
$$M\bold{\vec{v}}_{CM,f} = \sum_{j=1}^N m_j \bold{\vec{v}}_{j,f}$$Pero la conservación del momento nos dice que el lado derecho de ambas ecuaciones debe ser igual, o sea:
Este resultado implica que la conservación del momento se expresa en términos del centro de masa del sistema. Observa que cuando un objeto se mueve a través del espacio sin una fuerza externa neta actuando sobre él, una partícula individual del objeto puede acelerar en varias direcciones, con varias magnitudes, dependiendo de la fuerza interna neta que actúa sobre ese objeto en cualquier momento (recuerda, es solo la suma de vectores de todas las fuerzas internas que desaparece, no la fuerza interna de una sola partícula), Por lo tanto, el momento de esa partícula no será constante, pero el momento de todo el objeto extendido será, en acuerdo con la Ecuación 9.36.
La ecuación 9.36 implica otro resultado importante: como M representa la masa de todo el sistema de partículas, es necesariamente constante (de lo contrario, no tenemos un sistema cerrado, por lo que no podemos esperar que se conserve el momento del sistema).
Como resultado, la Ecuación 9.36 implica que, para un sistema cerrado,
Es decir, en ausencia de una fuerza externa, la velocidad del centro de masa nunca cambia.
Puedes sentirte tentado a encogerte de hombros y decir: "Bueno, sí, es la primera ley de Newton", pero recuerda que la primera ley de Newton discute la velocidad constante de una partícula, mientras que la ecuación 9.37 se aplica al centro de masa de una colección (posiblemente vasta) de partículas que interactúan, ¡y que no puede haber ninguna partícula en el centro de la masa en absoluto! Entonces, este es realmente un resultado notable.
Ejemplo 9.19
Exhibición de fuegos artificiales
Cuando explota un cohete de fuegos artificiales, miles de fragmentos brillantes vuelan hacia afuera en todas las direcciones y caen a la Tierra en una elegante y hermosa exhibición (Figura 9.31). Describe lo que sucede, en términos de la conservación del momento y del centro de masa.
La imagen muestra una simetría radial sobre los puntos centrales de las explosiones; esto sugiere la idea del centro de masa. También podemos ver el movimiento parabólico de las partículas brillantes; esto trae a la mente ideas de movimiento de proyectiles.

Solución
Inicialmente, el cohete de fuegos artificiales se lanza y vuela más o menos recto hacia arriba.
Esta es la causa del camino blanco, más o menos recto, que se adentra en el cielo por debajo de la explosión en la esquina superior derecha de la imagen (la explosión amarilla). Este camino no es parabólico porque el proyectil explosivo, durante su fase de lanzamiento, es en realidad un cohete; el impulso que se le aplica mediante la eyección del combustible en combustión aplica una fuerza sobre el proyectil durante el intervalo de tiempo de subida. El proyectil tiene múltiples fuerzas sobre él; por lo tanto, no está en caída libre antes de la explosión.
En el instante de la explosión, los miles de fragmentos brillantes vuelan hacia afuera en un patrón radialmente simétrico. La simetría de la explosión es el resultado de todas las fuerzas internas sumando cero, para cada fuerza interna, hay otra que es igual en magnitud y opuesta en dirección.
Sin embargo, como aprendimos anteriormente, estas fuerzas internas no pueden cambiar el momento del centro de masa del cohete (ahora explotado). Dado que la fuerza del cohete se ha desvanecido, el centro de masa del cohete es ahora un proyectil (la única fuerza sobre él es la gravedad), por lo que su trayectoria se vuelve parabólica. Las dos explosiones rojas a la izquierda muestran la ruta de sus centros de masa en un tiempo ligeramente más largo después de la explosión en comparación con la explosión amarilla en la esquina superior derecha.
De hecho, si miras detenidamente las tres explosiones, puedes ver que los senderos resplandecientes no son realmente radialmente simétricos; más bien, son algo más densos en un lado que en el otro. Específicamente, la explosión amarilla y la explosión media inferior son ligeramente más densas en sus lados derechos, y la explosión superior izquierda es más densa en su lado izquierdo. Esto se debe al momneto de sus centros de masa; las diferentes densidades de camino se deben al momento que cada pieza del proyectil tenía en el momento de su explosión.
El fragmento de la explosión en la esquina superior izquierda de la imagen tenía un momneto que apuntaba hacia arriba y hacia la izquierda; el momento del fragmento medio apuntaba hacia arriba y ligeramente hacia la derecha; y la explosión del lado derecho claramente hacia arriba y hacia la derecha (como lo demuestra el rastro de escape blanco del cohete visible debajo de la explosión amarilla).
Finalmente, cada fragmento es un proyectil en sí mismo, y traza miles de parábolas brillantes.
Explicación
En la discusión anterior, dijimos, "... el centro de masa del cohete ahora es un proyectil (la única fuerza sobre él es la gravedad) ...." Esto no es del todo exacto, ya que puede no haber ninguna masa en absoluto en el centro de masa; en cuyo caso, no podría haber una fuerza que actúe sobre él. Esto es en realidad una taquigrafía verbal para describir el hecho de que las fuerzas gravitatorias sobre todas las partículas actúan de modo que el centro de masa cambia de posición exactamente como si toda la masa del cohete estuviera siempre ubicada en la posición del centro de masa.
 Comprueba tu aprendizaje 9.13
Comprueba tu aprendizaje 9.13
A veces puedes escuchar a alguien describir una explosión diciendo algo así como "los fragmentos del objeto explotado siempre se mueven de una manera que asegura que el centro de masa continúe moviéndose en su trayectoria original".
Esto lo hace sonar como si el proceso es algo mágico: ¿cómo puede ser que, en cada explosión, siempre se resuelva que los fragmentos se mueven de la manera correcta para que el movimiento del centro de masa no cambie? Dicho de esta manera, sería difícil de creer que ninguna explosión haga algo diferente.
La explicación de esta coincidencia aparentemente sorprendente es:
definimos el centro de masa con precisión, así que esto es exactamente lo que obtendríamos. Recordemos que primero definimos el momento del sistema:
$$\bold{\vec{p}}_{CM} = \sum_{j=1}^N m_j\frac{d\bold{\vec{p}}_j}{dt}$$Luego llegamos a la conclusión de que la fuerza externa neta en el sistema (si corresponde) cambió este momento:
$$\bold{\vec{F}} = \frac{d\bold{\vec{p}}_{CM}}{dt}$$y luego, y aquí está el punto, definimos una aceleración que obedecería la segunda ley de Newton. Es decir, exigimos que podamos escribir
$$\begin{split} \bold{\vec{a}} &= \frac{\bold{\vec{F}}}{M}\\ &= \frac{d^2}{dt^2}\bigg(\frac{1}{M}\sum_{j=1}^Nm_jr\bold{\vec{r}}_j\bigg) \end{split}$$donde la cantidad dentro del paréntesis es el centro de masa de nuestro sistema. Entonces, no es sorprendente que el centro de masa obedezca a la segunda ley de Newton; lo definimos para que así sea.
El siguiente juego, diseñado por (Michal Goly), incorpora la conservación del momento al permitir que los meteoritos choquen entre sí. Con este juego, nos preparamos para el último apartado de este capítulo.
Propulsión de cohetes
Ahora tratamos el caso donde la masa de un objeto está cambiando. Analizamos el movimiento de un cohete, que cambia su velocidad (y por lo tanto su momento) al expulsar los gases combustibles quemados, lo que hace que se acelere en la dirección opuesta a la velocidad del combustible expulsado (Figura 9.32).

Específicamente: Un cohete con combustible completo en el espacio profundo tiene una masa total $m_0$ (incluye la masa inicial del combustible). En algún momento en el tiempo, el cohete tiene una velocidad $\bold{\vec{v}}$ y una masa $m$; esta masa es una combinación de la masa del cohete vacío y la masa del combustible restante no quemado que contiene (Nos referimos a m como la "masa instantánea" y $\bold{\vec{v}}$ como la "velocidad instantánea"). El cohete acelera quemando el combustible que transporta y expulsando los gases de escape quemados. Si la velocidad de combustión del combustible es constante, y la velocidad a la que se expulsa el escape también es constante, ¿cuál es el cambio de velocidad del cohete como resultado de quemar todo su combustible?
Análisis físico
Aquí hay una descripción de lo que sucede, para que tengas una idea de la física involucrada.
- A medida que operan los motores de los cohetes, expulsan continuamente gases combustibles que tienen tanto masa como velocidad y, por lo tanto, algún momento. Mediante la conservación del momento, el momento del cohete cambia por esta misma cantidad (con el signo opuesto). Supondremos que el combustible quemado se expulsa a una velocidad constante, lo que significa que la velocidad de cambio del momento del cohete también es constante. Por la ecuación 9.9, esto representa una fuerza constante en el cohete.
- Sin embargo, a medida que pasa el tiempo, la masa del cohete (que incluye la masa del combustible restante) disminuye continuamente. Por lo tanto, a pesar de que la fuerza en el cohete es constante, la aceleración resultante no lo es, está aumentando continuamente.
- Entonces, el cambio total de la velocidad del cohete dependerá de la cantidad de masa de combustible que se quema, y esa dependencia no es lineal.
El problema es que tiene que cambiar la masa y la velocidad del cohete; también, la masa total de gases expulsados está cambiando. Si definimos que nuestro sistema es el cohete + combustible, entonces este es un sistema cerrado (dado que el cohete está en el espacio profundo, no hay fuerzas externas que actúen sobre este sistema); como resultado, se conserva el momento para este sistema. Por lo tanto, podemos aplicar la conservación del momento para responder a la pregunta (Figura 9.33).
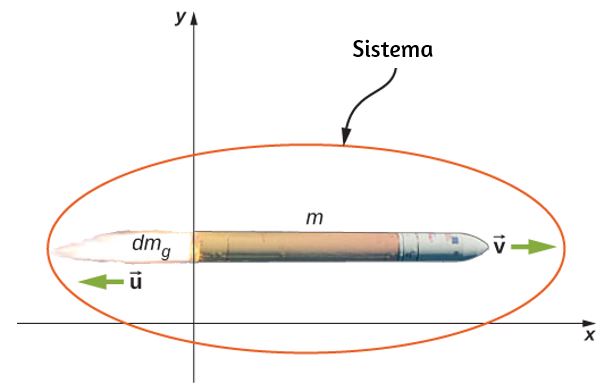
En el mismo momento en que la masa instantánea total del cohete es $m$ (es decir, $m$ es la masa del cuerpo del cohete más la masa del combustible en ese momento), definimos la velocidad instantánea del cohete como $\bold{\vec{v}} = v\^{\bold{i}}$ (positiva dirección $x$); esta velocidad se mide en relación con un sistema de referencia inercial (la Tierra, por ejemplo). Por lo tanto, el impulso inicial del sistema es
$$\bold{\vec{p}}_i = mv\^{\bold{i}}$$Los motores del cohete están quemando combustible a un ritmo constante y expulsando los gases de escape en la dirección $-x$. Durante un intervalo de tiempo infinitesimal $dt$, los motores expulsan una masa infinitesimal (positiva) de gas $dm_g$ a la velocidad $\bold{\vec{u}} = -u\^{\bold{i}}$. Ten en cuenta que aunque la velocidad del cohete $v\^{\bold{i}}$ se mide con respecto a la Tierra, la velocidad del gas de escape se mide con respecto al cohete (en movimiento). Medido con respecto a la Tierra, por lo tanto, el gas de escape tiene velocidad $(v-u)\^{\bold{i}}$.
Como consecuencia de la eyección del gas de combustible, la masa del cohete disminuye en $dm_g$, y su velocidad aumenta en $dv\^{\bold{i}}$. Por lo tanto, incluyendo tanto el cambio para el cohete como el cambio para el gas de escape, el momento final del sistema es
$$\bold{\vec{p}}_f = \bold{\vec{p}}_{cohete} + \bold{\vec{p}}_{gas} = (m - dm_g)(v + dv)\^{\bold{i}} + dm_g(v - u)\^{\bold{i}}$$Como todos los vectores están en la dirección $x$, soltamos la notación vectorial. Aplicando la conservación del momento, obtenemos
$$p_i = p_f$$ $$mv = (m − dm_g)(v + dv)+dm_g(v − u)$$Ahora, $dm_g$ y $dv$ son muy pequeños; por lo tanto, su producto $dm_gdv$ es muy, muy pequeño, mucho más pequeño que los otros dos términos en esta expresión. Despreciamos este término, y obtenemos:
$$mdv = dm_gu$$Nuestro siguiente paso es recordar que, dado que $dm_g$ representa un aumento en la masa de gases eyectados, también debe representar una disminución de la masa del cohete:
$$dm_g = -dm$$Sustituyendo esto, tenemos
$$mdv = -dmu$$o
$$dv = -u\frac{dm}{m}$$La integración desde la masa inicial $m_i$ a la masa final $m$ del cohete nos da el resultado que buscamos:
$$\int_{v_i}^v dv = -u\int_{m_i}^m \frac{1}{m} dm$$ $$v - v_i = u\;ln\Big(\frac{m_i}{m}\Big)$$y así nuestra respuesta final es
Este resultado se llama ecuación de cohete. Fue originalmente deducida por el físico soviético Konstantin Tsiolkovsky en 1897. Nos da el cambio de velocidad que obtiene el cohete al quemar una masa de combustible que disminuye la masa total del cohete desde $m_0$ hasta $m$. Como se esperaba, la relación entre $\Delta v$ y el cambio de masa del cohete no es lineal.
Estrategia de resolución de problemas: cohete de propulsión
En los problemas con los cohetes, las preguntas más comunes son encontrar el cambio de velocidad debido a la quema de cierta cantidad de combustible durante cierto tiempo; o para determinar la aceleración que resulta de la quema de combustible.
- Para determinar el cambio de velocidad, usa la ecuación de cohete 9.38.
- Para determinar la aceleración, determina la fuerza usando el teorema impulso-momento, usando la ecuación del cohete para determinar el cambio de velocidad.
Ejemplo 9.20
Empuje en una nave espacial
Una nave espacial se mueve en un espacio libre de gravedad a lo largo de un camino recto cuando su piloto decide acelerar hacia adelante.
Enciende los propulsores y el combustible quemado se expulsa a una velocidad constante de $2,0 \times 10^2 kg/s$, a una velocidad (relativa al cohete) de $2,5 \times 10^2 m/s$. La masa inicial de la nave espacial y su combustible no quemado es de $2,0 \times 10^4 kg$, y los propulsores están encendidos durante $30 s$.
a. ¿Cuál es el empuje (la fuerza aplicada al cohete por el combustible expulsado) en la nave espacial?
b. ¿Cuál es la aceleración de la nave espacial en función del tiempo?
c. ¿Cuáles son las aceleraciones de la nave en $t = 0, 15, 30$ y $35 s$?
Estrategia
a. La fuerza en la nave espacial es igual a la velocidad de cambio del momento del combustible.
b. Conociendo la fuerza de la parte (a), podemos usar la segunda ley de Newton para calcular la aceleración consiguiente. La clave aquí es que, aunque la fuerza aplicada a la nave espacial es constante (el combustible se expulsa a una velocidad constante), la masa de la nave espacial no lo está, por lo tanto, la aceleración causada por la fuerza no será constante. Esperamos obtener una función $a(t)$, por lo tanto.
c. Usaremos la función que obtenemos en la parte (b), y simplemente sustituiremos los datos dados. Importante: esperamos que la aceleración aumente con el paso del tiempo, ya que la masa que se está acelerando disminuye continuamente (el combustible se expulsa del cohete).
Solución
a. El momento del gas combustible expulsado es
$$p = m_gv$$La velocidad de eyección $v = 2.5 \times 10^2 m/s$ es constante, y por lo tanto la fuerza es
$$F = \frac{dp}{dt} = v\frac{dm_g}{dt} = -v\frac{dm}{dt}$$Ahora, $dm_g/dt$ es la tasa de cambio de la masa del combustible; el problema indica que esto es $2.0 \times 10^2 kg/s$. Sustituyendo, obtenemos
$$\begin{split} F &= v\frac{dm_g}{dt}\\ &= (2.5 \times 10^2 m/s)(2.0 \times 10^2 kg/s)\\ &= 5 \times 10^4 N \end{split}$$b. Anteriormente, definimos $m$ como la masa combinada del cohete vacío más el combustible sin quemar que contenía: $m = m_R + _g$. De la segunda ley de Newton,
$$a = \frac{F}{m} = \frac{F}{m_R + m_g}$$La fuerza es constante y la masa de cohete vacía $m_R$ es constante, pero la masa de combustible $m_g$ está disminuyendo a una velocidad uniforme; específicamente:
$$m_g = m_g(t) = m_{g0} − \Big(\frac{dm_g}{d}\Big)t$$Esto nos da
$$a(t) = \frac{F}{m_{gi} − (dm_g/dt)t} = \frac{F}{M − (dm_g/dt)t}$$Ten en cuenta que, como se esperaba, la aceleración es una función del tiempo. Sustituyendo los datos dados:
$$a(t) = \frac{5 \times 10^4 N}{2.0 \times 10^4 kg − (2.0 \times 10^2 kg/s)t}$$c. En $t = 0 s$
$$a(0 s) = \frac{5 \times 10^4 N}{2.0 \times 10^4 kg − (2.0 × 10^2 kg/s)(0 s)} = 2.5 m/s^2$$En $t = 15 s, a(15 s) = 2.9 m/s^2$.
En $t = 30 s, a(30 s) = 3.6 m/s^2$.
La aceleración está aumentando, como esperábamos.
Explicación
Ten en cuenta que la aceleración no es constante; como resultado, cualquier cantidad dinámica debe calcularse utilizando integrales o (más fácilmente) la conservación de la energía total.
 Comprueba tu aprendizaje 9.14
Comprueba tu aprendizaje 9.14
Cohete en un campo gravitacional
Analicemos ahora el cambio de velocidad del cohete durante la fase de lanzamiento, desde la superficie de la Tierra.
Para mantener la matemática manejable, restringiremos nuestra atención a las distancias para las cuales la aceleración causada por la gravedad se puede tratar como una constante $g$.
El análisis es similar, excepto que ahora hay una fuerza externa de $\bold{\vec{F}} = -mg\^{\bold{j}}$ que actúa en nuestro sistema. Esta fuerza aplica un impulso $d\bold{\vec{J}} = \bold{\vec{F}}dt = -mgdt\^{\bold{j}}$, que es igual al cambio de momento. Esto nos da
$$d\bold{\vec{p}} = d\bold{\vec{J}}$$ $$\bold{\vec{p}}_f - \bold{\vec{p}}_i = −mgdt\^{\bold{j}}$$ $$[(m − dm_g)(v + dv) + dm_g( v− u) − mv]\^{\bold{j}} = −mgdt\^{\bold{j}}$$y entonces
$$mdv − dm_gu = −mgdt$$donde nuevamente hemos despreciado el término $dm_gdv$ y hemos dejado de lado la notación vectorial. Luego reemplazando $dm_g$ con $-dm$:
$$mdv + dmu = −mgdt\\ mdv = −dmu − mgdt$$dividiendo por m, obtenemos
$$dv = −u\frac{dm}{m} − gdt$$e integrando, tenemos
Como era de esperar, la velocidad del cohete se ve afectada por la aceleración (constante) de la gravedad.
Recuerda que $\Delta t$ es el tiempo de combustión del combustible. Ahora, en ausencia de gravedad, la Ecuación 9.38 implica que no importa cuánto tiempo lleve quemar la masa completa de combustible; el cambio de velocidad no depende de $\Delta t$. Sin embargo, en presencia de la gravedad, importa mucho.
El término $-g\Delta t$ en la ecuación 9.39 nos dice que cuanto más largo sea el tiempo de combustión, menor será el cambio de velocidad del cohete. Esta es la razón por la cual el lanzamiento de un cohete es tan espectacular en el primer momento del despegue: es esencial quemar el combustible lo más rápido posible, para obtener un $\Delta v$ lo más grande posible.
En este puzle, diseñado por Juan Guillermo Rivera B., descubre algunas de las imágenes presentadas en este capítulo.
Gravitación
Henry Cavendish (10 de octubre de 1731-Londres, Reino Unido, 24 de febrero de 1810) fue un físico y químico. Como físico, es conocido por el experimento de Cavendish (mediante el que posteriormente se determinó la constante de gravitación universal) (https://es.wikipedia.org/)
Introducción

En este capítulo, estudiamos la naturaleza de la fuerza gravitacional para objetos tan pequeños como nosotros mismos y para sistemas tan masivos como galaxias enteras. Mostramos cómo la fuerza gravitacional afecta a los objetos en la Tierra y al movimiento del Universo mismo. La gravedad es la primera fuerza que se postula como una fuerza de acción a distancia.
Es decir, los objetos ejercen una fuerza gravitacional el uno sobre el otro sin contacto físico y esa fuerza cae a cero solo a una distancia infinita. La Tierra ejerce una fuerza gravitatoria sobre ti, pero también lo hacen nuestro Sol, la galaxia de la Vía Láctea y los miles de millones de galaxias, como las que se muestran en la figura, que son tan distantes que no podemos verlas a simple vista.
En el siguiente objeto interactivo, diseñado por Carlos Alberto Jaimes Vergara, identifica la relación entre la distancia y la fuerza de atracción gravitacional que experimentan los cuerpos, a partir de la representación vectorial de estas magnitudes y de la interpretación de gráficas de fuerza-distancia.
Ley de gravitación universal de Newton
Primero revisamos la historia del estudio de la gravitación, con énfasis en aquellos fenómenos que durante miles de años han inspirado a filósofos y científicos en buscar una explicación. Luego examinamos la forma más simple de la ley de gravitación universal de Newton y cómo aplicarla.
La historia de la gravitación
Los filósofos más antiguos se preguntaban por qué los objetos, naturalmente, tienden a caer al suelo. Aristóteles (384-322 a.C.) creía que era la naturaleza de las rocas buscar la Tierra y la naturaleza del fuego buscar los Cielos. Brahmagupta (598 ~ 665 d.C.) postuló que la Tierra era una esfera y que los objetos poseían una afinidad natural por ella, cayendo hacia el centro desde donde estaban ubicados.
Los movimientos del Sol, nuestra Luna y los planetas también se han estudiado durante miles de años. Estos movimientos fueron descritos con asombrosa precisión por Ptolomeo (90-168 d.C.), cuyo método de epiciclos describía las rutas de los planetas como círculos dentro de círculos. Sin embargo, hay poca evidencia de que alguien conectara el movimiento de los cuerpos astronómicos con el movimiento de los objetos que caen a la Tierra, hasta el siglo diecisiete.
Nicolás Copérnico (1473-1543) es generalmente reconocido como el primero en desafiar el sistema geocéntrico de Ptolomeo (centrado en la Tierra) y sugerir un sistema heliocéntrico, en el que el Sol está en el centro del sistema solar. Esta idea fue apoyada por las medidas increíblemente precisas a simple vista de los movimientos planetarios de Tycho Brahe y su análisis por Johannes Kepler y Galileo Galilei.
La siguiente escena interactiva, diseñada por José Luis Abreu León del Instituto de Matemáticas, UNAM, permite observar las evoluciones del Sol y los planetas desde fuera de la Tierra. Puedes elegir realizar la observación con la Tierra en el centro de las evoluciones o con el Sol. Así comprobarás que las trayectorias de los planetas son mucho más sencillas de describir cuando se coloca al Sol en el centro del movimiento.
Kepler demostró que el movimiento de cada planeta es una elipse (la primera de sus tres leyes, tratada en las Leyes de movimiento planetario de Kepler), y Robert Hooke (el mismo Hooke que formuló la ley de Hooke para resortes) sugirió intuitivamente que estos movimientos se deben a que los planetas se sienten atraídos por el sol. Sin embargo, fue Isaac Newton quien conectó la aceleración de objetos cerca de la superficie de la Tierra con la aceleración centrípeta de la Luna en su órbita alrededor de la Tierra.
Finalmente, en la Teoría de la Gravedad de Einstein, observamos la teoría de la relatividad general propuesta por Albert Einstein en 1916. Su teoría proviene de una perspectiva muy diferente, en la que la gravedad es una manifestación de la deformación en el espacio-tiempo de la masa. Las consecuencias de su teoría dieron lugar a muchas predicciones notables, esencialmente todas las cuales se han confirmado durante las décadas posteriores a la publicación de la
teoría (incluida la medición de 2015 de las ondas gravitacionales a partir de la fusión de dos agujeros negros).
Ley de Gravitación Universal de Newton
Newton notó que los objetos en la superficie de la Tierra (por lo tanto a una distancia de $R_E$ del centro de la Tierra) tienen una aceleración de $g$, pero la Luna, a una distancia de aproximadamente $60R_E$, tiene una aceleración centrípeta aproximadamente $60$ veces menor que $g$. Podrías explicar esto postulando que existe una fuerza entre dos objetos cualquiera, cuya magnitud viene dada por el producto de las dos masas dividido por el cuadrado de la distancia entre ellos. Ahora sabemos que esta ley del cuadrado inverso es de naturaleza omnipresente, una función de la geometría para las fuentes puntuales. La fuerza de cualquier fuente a una distancia $r$ se extiende sobre la superficie de una esfera centrada alrededor de la masa. El área de superficie de esa esfera es proporcional a $r^2$.
La ley de gravitación de Newton se puede expresar como $$\bold{\vec{F}}_{12} = G\frac{m_1m_2}{^2}\^{\bold{r}}_{12}\tag{10.1}$$ donde $\bold{\vec{F}}_{12}$ es la fuerza en el objeto $1$ ejercida por el objeto $2$ y $\^{\bold{r}}_{12}$ es un vector unitario que apunta desde el objeto $1$ hacia el objeto $2$.
Como se muestra en la figura 10.2, el vector$\bold{\vec{F}}_{12}$ apunta desde el objeto $1$ hacia el objeto $2$, y por lo tanto representa una fuerza atractiva entre los objetos.
La fuerza igual pero opuesta $\bold{\vec{F}}_{21}$ es la fuerza sobre el objeto $2$ ejercida por el objeto $1$.
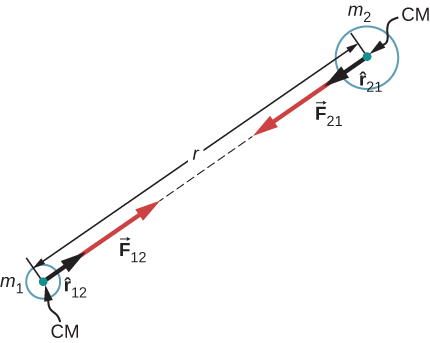
El experimento de Cavendish
Un siglo después de que Newton publicara su ley de la gravitación universal, Henry Cavendish determinó la constante de proporcionalidad G realizando un experimento minucioso. Construyó un dispositivo similar al que se muestra en la figura 10.3, en el que pequeñas masas están suspendidas de un cable. Una vez en equilibrio, dos masas fijas y más grandes se colocan simétricamente cerca de las más pequeñas. La atracción gravitacional crea una torsiónen el cable de soporte que se puede medir.
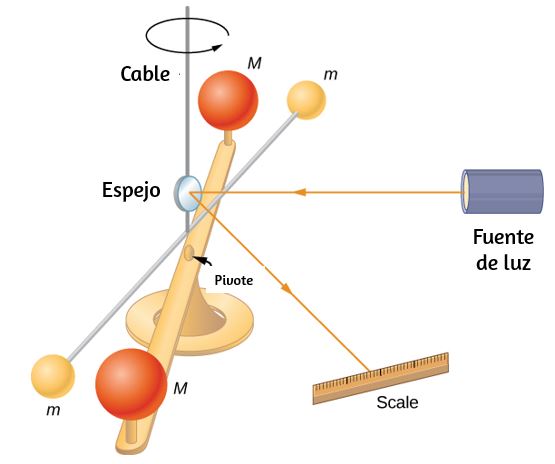
La constante $G$ se denomina constante gravitacional universal y Cavendish determinó que es $G = 6.67 \times 1^{-11} N\cdot m^2/kg^2$. La palabra "universal" indica que los científicos piensan que esta constante se aplica a las masas de cualquier composición y que es la misma en todo el Universo. El valor de $G$ es un número increíblemente pequeño, que muestra que la fuerza de la gravedad es muy débil. La atracción entre masas tan pequeñas como nuestros cuerpos, o incluso objetos del tamaño de un rascacielos, es increíblemente pequeña. Por ejemplo, dos masas de $1.0 kg$ ubicadas a $1.0 metro$ de distancia ejercen una fuerza de $6.7 \times 10^{-11} N$ entre sí. Este es el peso de un grano típico de polen.
Aunque la gravedad es la más débil de las cuatro fuerzas fundamentales de la naturaleza, su naturaleza atractiva es lo que nos mantiene en la Tierra, hace que los planetas orbiten alrededor del Sol y el Sol en órbita alrededor de nuestra galaxia, y une galaxias en racimos, desde unas pocas hasta millones . La gravedad es la fuerza que forma el Universo.
Estrategia de resolución de problemas: ley de gravitación de Newton
Para determinar el movimiento causado por la fuerza gravitatoria, sigue estos pasos:
- Identifica las dos masas, una o ambas, para las cuales deseas encontrar la fuerza gravitacional.
- Dibuja un diagrama de cuerpo libre, dibuja la fuerza que actúa sobre cada masa e indica la distancia entre sus centros de masa.
- Aplica la segunda ley de movimiento de Newton a cada masa para determinar cómo se moverá.
Ejemplo 10.1
Una colisión en órbita
Considera dos vehículos de carga útil Soyuz casi esféricos, en órbita alrededor de la Tierra, cada uno con una masa de $9000 kg$ y un diámetro de $4,0 m$. Inicialmente descansan entre sí, a $10.0 m$ de centro a centro. (Como veremos en Las leyes del movimiento planetario de Kepler, ambos orbitan la Tierra a la misma velocidad e interactúan casi igual que si estuvieran aislados en el espacio profundo). Determina la fuerza de gravedad entre ellos y su aceleración inicial. Calcula cuánto tiempo les toma a la deriva y qué tan rápido se mueven al impactar.
Estrategia
Usamos la ley de gravitación de Newton para determinar la fuerza entre ellos y luego usamos la segunda ley de Newton para encontrar la aceleración de cada uno. Para la estimación, suponemos que esta aceleración es constante, y usamos las ecuaciones de aceleración constante para encontrar el tiempo y la velocidad de la colisión.
Solución
La magnitud de la fuerza es
$$\begin{split} |\bold{\vec{F}}_{12}| &= F_{12} = G\frac{m_1m_2}{r^2}\\ &= 6.67 \times 10^{−11} N\cdot m^2/kg^2 \frac{(9000 kg)(9000 kg)}{(10 m)^2}\\ &= 5.4 \times 10^{−5} N \end{split}$$La aceleración inicial de cada carga útil es
$$a = \frac{F}{m} = \frac{5.4 \times 10^{−5} N }{9000 kg} = 6.0 \times 10^{−9} m/s^2$$Los vehículos tienen un diámetro de $4.0 m$, por lo que los vehículos se mueven de $10.0 m$ a $4.0 m$ de distancia, o una distancia de $3.0 m $cada uno. Un cálculo similar al anterior, para cuando los vehículos están a $4.0 m$ de distancia, produce una aceleración de $3.8 \times 10^{−8} m/s^2$, y el promedio de estos dos valores es $2.2 \times 10^{−8} m/s^2$. Si asumimos una aceleración constante igual a este valor y que comienzan desde el reposo, entonces los vehículos colisionan con la velocidad dada por
$$v^2 = v_0^2 + 2a(x − x_0)$$donde $v_0 = 0$, entonces
$$v = \sqrt{2(2.2 \times 10^{−9} N)(3.0m)} = 3.6 \times 10^{−4} m/s$$Usamos $v = v_0 + at$ para encontrar $t = v/a = 1.7 \times 10^4> s$ o aproximadamente $4.6$ horas.
Explicación
Estos cálculos, incluida la fuerza inicial, son solo estimaciones, ya que los vehículos probablemente no son esféricamente simétricos. Pero puedes ver que la fuerza es increíblemente pequeña. Los astronautas deben atarse a sí mismos cuando trabajen fuera incluso de la enorme Estación Espacial Internacional (EEI), como en la figura 10.4, porque la atracción gravitacional no puede salvarlos ni siquiera de la menor presión de la estación.

 Comprueba tu aprendizaje 10.1
Comprueba tu aprendizaje 10.1
El efecto de la gravedad entre dos objetos con masas en el orden de estos vehículos espaciales es realmente pequeño. Sin embargo, el efecto de la gravedad sobre ti desde la Tierra es tan significativo que una caída a la Tierra de solo unos pocos pies puede ser peligrosa. Examinamos la fuerza de la gravedad cerca de la superficie de la Tierra en la siguiente sección.
Ejemplo 10.2
Atracción entre las galaxias
Encuentra la aceleración de nuestra galaxia, la Vía Láctea, debido a la galaxia de tamaño comparable más cercana, la galaxia de Andrómeda (Figura 10.5).
La masa aproximada de cada galaxia es de $800$ mil millones de masas solares (una masa solar es la masa de nuestro Sol), y están separadas por $2,5$ millones de años luz (ten en cuenta que la masa de Andrómeda no es tan conocida, pero se cree que es un poco más grande que nuestra galaxia). Cada galaxia tiene un diámetro de aproximadamente $100.000$ años luz ($1 \;luz-año = 9.5 \times 10^{15} m$).
Estrategia
Como en el ejemplo anterior, usamos la ley de gravitación de Newton para determinar la fuerza entre ellos y luego usamos la segunda ley de Newton para encontrar la aceleración de la Vía Láctea. Podemos considerar las galaxias como masas puntuales, ya que sus tamaños son aproximadamente $25$ veces más pequeños que su separación. La masa del Sol es de $2.0 \times 10^{30} kg$ y un año luz es la distancia que la luz viaja en un año, $9.5 \times 10^{15} m$.

Solución
La magnitud de la fuerza es
$$\bold{\vec{F}}_{12} = G\frac{m_1m_2}{r^2}$$La aceleración de la Vía Láctea es
$$a = \frac{F}{m} = \frac{3.0 \times 10^{29} N }{(800 \times 10^9)(2.0 \times 10^{30} kg)} = 1.9 \times 10^{−13} m/s^2$$Explicación
¿Este valor de aceleración parece asombrosamente pequeño? Si comienzan desde el reposo, acelerarían directamente el uno hacia el otro, "colisionando" en su centro de masa.
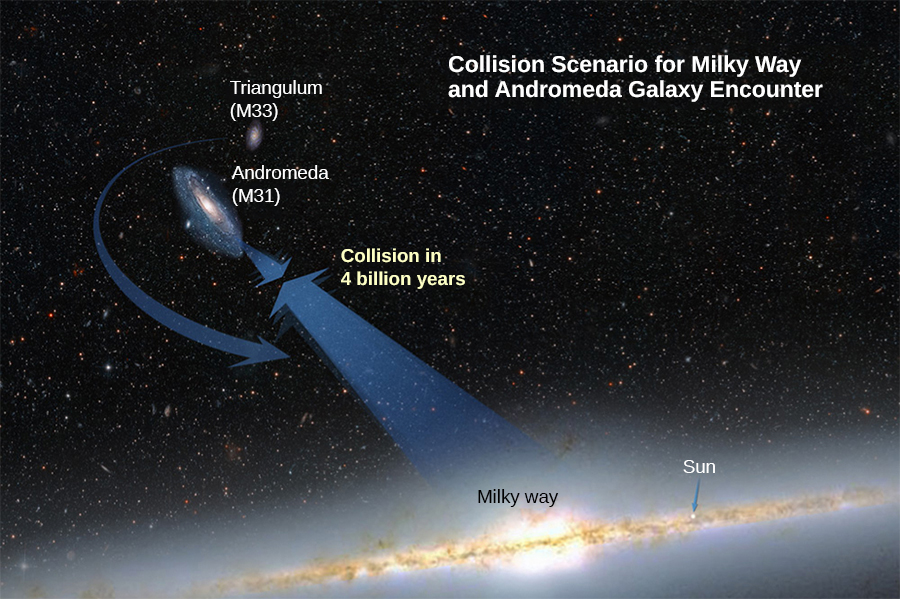
Estimemos el tiempo para que esto suceda. La aceleración inicial es $\approx 10-13 m/s^2$, entonces usando $v = at$, vemos que tomaría $\approx 10^{13}s$ para que cada galaxia alcance una velocidad de $1.0 m/s$, y estarían solo $\approx 0.5 \times 10^{13} m$ más cerca. Eso es nueve órdenes de magnitud más pequeño que la distancia inicial entre ellos. En realidad, tales movimientos son raramente simples. Estas dos galaxias, junto con alrededor de otras $50$ galaxias más pequeñas, están todas unidas gravitacionalmente en nuestro racimo local. Nuestro racimo local está ligado gravitacionalmente a otros racimos en lo que se llama un supercúmulo. Todo esto es parte de la gran danza cósmica que resulta de la gravitación, como se muestra en la figura 10.6.
Gravitación cerca de la superficie de la Tierra
En esta sección, observaremos cómo se aplica la ley de gravitación de Newton en la superficie de un planeta y cómo se conecta con lo que aprendimos antes sobre la caída libre. También examinaremos los efectos gravitacionales dentro de los cuerpos esféricos.
Peso
Recuerda que la aceleración de un objeto que cae libremente cerca de la superficie de la Tierra es aproximadamente $g = 9.80 m/s^2$. La fuerza que causa esta aceleración se denomina peso del objeto y, según la segunda ley de Newton, tiene el valor de $mg$. Ahora sabemos que esta fuerza es la fuerza gravitacional entre el objeto y la Tierra. Si sustituimos mg por la magnitud de $\bold{\vec{F}}_{12}$ en la ley de Newton de la gravitación universal, $m$ por $m_1$ y $M_E$ por $m_2$, obtenemos la ecuación escalar
$$mg = G\frac{mM_E}{r^2}$$donde $r$ es la distancia entre los centros de masa del objeto y la Tierra. El radio promedio de la Tierra es de aproximadamente $6370 km$. Por lo tanto, para objetos dentro de unos pocos kilómetros de la superficie de la Tierra, podemos tomar $r = R_E$ (Figura 10.7). La masa $m$ del objeto se cancela, obteniendo:
Esto explica por qué todas las masas caen libremente con la misma aceleración. Hemos ignorado el hecho de que la Tierra también acelera hacia el objeto que cae, pero eso es aceptable siempre y cuando la masa de la Tierra sea mucho más grande que la del objeto.
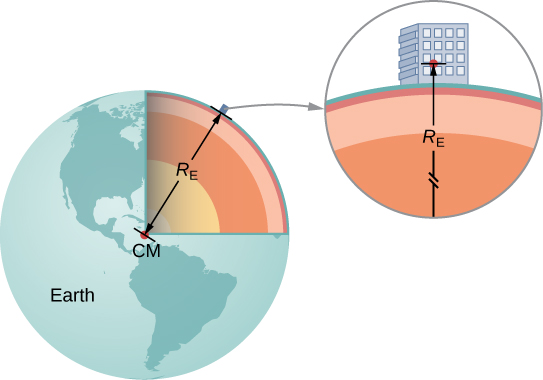
Ejemplo 10.3
Masas de la tierra y la luna
¿Te has preguntado alguna vez cómo conocemos la masa de la Tierra? Ciertamente no podemos ubicarlo en una escala. Los valores de g y el radio de la Tierra se midieron con una precisión razonable hace siglos.
a. Usa los valores estándar de $g, R_E$ y la Ecuación 10.2 para encontrar la masa de la Tierra.
b. Estima el valor de $g$ en la Luna. Usa el hecho de que la Luna tiene un radio de aproximadamente $1700 km$ (un valor de esta precisión se determinó hace muchos siglos) y supón que tiene la misma densidad promedio que la Tierra, $5500 kg/m^3$.
Estrategia
Con los valores conocidos de $g$ y $R_E$, podemos usar la Ecuación 10.2 para encontrar $M_E$. Para la Luna, usamos la suposición de densidad promedio igual para determinar la masa a partir de una relación de los volúmenes de la Tierra y la Luna.
Solución
a. Reordenando la Ecuación 10.2, tenemos
$$M_E = \frac{gR_E^2}{G} = \frac{9.80 m/s^2(6.37 \times 10^6 m)^2} {6.67 \times 10^{-11} N\cdot m^2/kg^2} = 5.95 \times 10^{24} kg$$b. El volumen de una esfera es proporcional al radio al cubo, por lo que una proporción simple nos da
Ahora usamos la Ecuación 10.2.
$$\begin{split} g_M &= G\frac{M_M}{r_M^2}\\ &= (6.67 \times 10^{-11} N\cdot m^2/kg^2)\frac{1.1 \times 10^{23} kg}{(1.7 \times 10^6 m)^2}\\ &= 2.5 m/s^2 \end{split}$$Explicación
Tan pronto como Cavendish determinó el valor de $G$ en 1798, se pudo calcular la masa de la Tierra (De hecho, ese fue el objetivo final del experimento de Cavendish). El valor que calculamos para $g$ de la Luna es incorrecto. La densidad promedio de la Luna es de solo $3340 kg/m^3$ y $g = 1.6 m/s^2$ en la superficie. Newton intentó medir la masa de la Luna comparando el efecto del Sol sobre las mareas oceánicas de la Tierra en comparación con el de la Luna. Su valor era un factor de dos demasiado pequeño. Los valores más precisos para g y la masa de la Luna provienen del seguimiento del movimiento de las naves espaciales que han orbitado alrededor de la Luna. Pero la masa de la Luna en realidad se puede determinar con precisión sin ir a la Luna. La Tierra y la Luna orbitan alrededor de un centro común de masa, y las cuidadosas mediciones astronómicas pueden determinar esa ubicación.
La relación entre la masa de la Luna y la de la Tierra es la relación entre (la distancia desde el centro de masa común hasta el centro de la Luna) y (la distancia desde el centro de masa común al centro de la Tierra).
Más adelante en este capítulo, veremos que la masa de otros cuerpos astronómicos también puede determinarse por el período de pequeños satélites que orbitan alrededor de ellos. Pero hasta que Cavendish determinó el valor de G, las masas de todos estos cuerpos eran desconocidas.
Ejemplo 10.4
Gravedad sobre la superficie de la Tierra
¿Cuál es el valor de $g$ a $400 km$ sobre la superficie de la Tierra, donde la Estación Espacial Internacional está en órbita?
Estrategia
Usando el valor de $M_E$ y observando que el radio es $r = R_E + 400 km$, usamos la Ecuación 10.2 para hallar $g$.
De la ecuación 10.2 tenemos
$$\begin{split} g &= G\frac{M_E}{r^2}\\ &= 6.67 \times 10^{-11} N\cdot m^2/kg^2\frac{5.96 \times 10^{24} kg}{(6.37 \times 10^6 + 400 \times 10^3 m)^6}\\ &= 8.67 m/s^2 \end{split}$$A menudo vemos videos de astronautas en estaciones espaciales, aparentemente sin peso.
Pero claramente, la fuerza de la gravedad actúa sobre ellos. Comparando el valor de g que calculamos con el de la Tierra ($9.80 m/s^2$), vemos que los astronautas de la Estación Espacial Internacional aún tienen el $88\%$ de su peso. Solo parecen ser ingrávidos porque están en caída libre.
 Comprueba tu aprendizaje 10.2
Comprueba tu aprendizaje 10.2
Poniendo en órbita los satélites
En el siguiente objeto interactivo, diseñado por James Abbatiello, trata de poner en órbita un satélite.
Haz clic para poner el satélite y arrástralo para darle un empujón. No te exageres con el empujón, pues podrías enviar el satélite a otra galaxia.
Cosas para explorar
- ¿Puedes poner un satélite en órbita alrededor de la Tierra?
- ¿Es más fácil poner algo en órbita cerca de la Tierra o más lejos?
- ¿Hay alguna diferencia en la dificultad para obtener satélites orbitando en el sentido de las agujas del reloj y no en el sentido contrario?
- ¿Puedes poner un satélite en órbita alrededor de la Luna?
- Qué sucede con los satélites que orbitan alrededor de la Tierra a aproximadamente la misma distancia que la Luna?
- ¿Puedes iniciar un satélite fuera de la órbita de la Luna y hacer que se establezca en una órbita dentro de la órbita de la Luna? ¿Por qué o por qué no?
El campo gravitacional
La ecuación 10.2 es una ecuación escalar, que da la magnitud de la aceleración gravitacional como una función de la distancia desde el centro de la masa que causa la aceleración. Pero podríamos haber conservado la forma vectorial de la fuerza de la gravedad en la Ecuación 10.1, y escribir la aceleración en forma vectorial como
$$\bold{\vec{g}} = G\frac{M}{r^2}\^{\bold{r}}$$Identificamos el campo vectorial representado por $\bold{\vec{g}}$ como el campo gravitatorio causado por la masa $M$. Podemos imaginar el campo como se muestra en la figura 10.8. Las líneas se dirigen radialmente hacia adentro y se distribuyen simétricamente alrededor de la masa.
Como sucede con cualquier campo vectorial, la dirección de $\bold{\vec{g}}$ es paralela a las líneas de campo en cualquier punto. La intensidad de $\bold{\vec{g}}$ en cualquier punto es inversamente proporcional al espaciado entre líneas. Otra forma de decir esto es que la magnitud del campo en cualquier región es proporcional al número de líneas que pasan a través de un área de superficie unitaria, efectivamente es una densidad de líneas. Dado que las líneas están equiespaciadas en todas las direcciones, el número de líneas por unidad de superficie a una distancia $r$ de la masa es el número total de líneas divididas por el área de superficie de una esfera de radio $r$, que es proporcional a $r^2$. Por lo tanto, esta imagen representa perfectamente la ley del cuadrado inverso, además de indicar la dirección del campo. En la imagen de campo, decimos que una masa m interactúa con el campo gravitacional de la masa $M$. Utilizaremos el concepto de campos con gran ventaja en los capítulos posteriores sobre electromagnetismo del volumen II de Física.
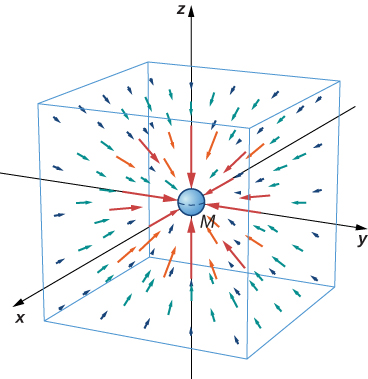
Peso aparente: Contabilización de la rotación de la Tierra
Como vimos en las aplicaciones de las Leyes de Newton, los objetos que se mueven a velocidad constante en un círculo tienen una aceleración centrípeta dirigida hacia el centro del círculo, lo que significa que debe haber una fuerza neta dirigida hacia el centro de ese círculo. Como todos los objetos en la superficie de la Tierra se mueven a través de un círculo cada $24$ horas, debe haber una fuerza centrípeta neta en cada objeto dirigido hacia el centro de ese círculo.
Consideremos primero un objeto de masa $m$ ubicado en el ecuador, suspendido de una pesa (Figura 10.9). La pesa (medidor de peso) ejerce una fuerza hacia arriba $\bold{\vec{F}}$ lejos del centro de la Tierra. Esta es la lectura en la pesa, y por lo tanto es el peso aparente del objeto. El peso ($mg$) apunta hacia el centro de la Tierra. Si la Tierra no estuviera girando, la aceleración sería cero y, en consecuencia, la fuerza neta sería cero, lo que da como resultado $F_s = mg$. Esta sería la verdadera lectura del peso.
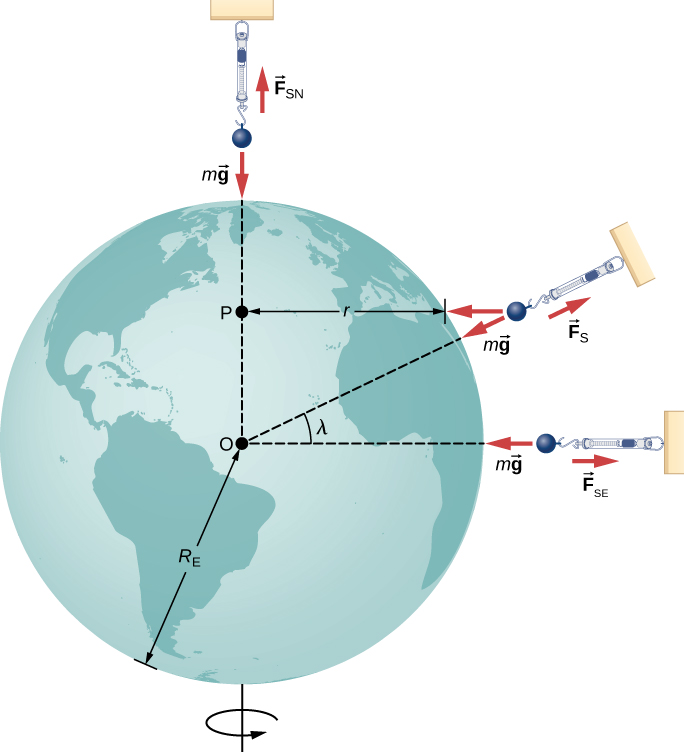
Con la rotación, la suma de estas fuerzas debe proporcionar la aceleración centrípeta, $a_c$. Usando la segunda ley de Newton, tenemos:
Ten en cuenta que $a_c$ apunta en la misma dirección que el peso; por lo tanto, es negativo. La velocidad tangencial $v$ es la velocidad en el ecuador y $r$ es $R_E$. Podemos calcular la velocidad simplemente observando que los objetos en el ecuador recorren la circunferencia de la Tierra en $24$ horas. En su lugar, usemos la expresión alternativa para $a_c$ vista en el capítulo de cinemática en dos y tres dimensiones.
Recuerda que la velocidad tangencial está relacionada con la velocidad angular ($\omega$) mediante $v = r\omega$. Por lo tanto, tenemos $a_c = -r\omega^2$. Al reordenar la ecuación 10.3 y sustituir $r$ por $R_E$, el peso aparente en el ecuador es
$$F_s = m(g - R_E\omega^2)$$La velocidad angular de la Tierra en todas partes es
$$\omega = \frac{2π\;rad}{24 h \times 3600 s/h} = 7.27 \times 10^{−5} rad/s$$Sustituyendo los valores de $R_E$ y $\omega$, tenemos $R_E\omega^2 = 0.0337 m/s^2$. Esto es solo el $0,34\%$ del valor de la gravedad, por lo que es claramente una pequeña corrección.
Ejemplo 13.5
Peso aparente cero
¿Qué tan rápido necesitaría la Tierra girar para que los que están en el ecuador tengan un peso aparente cero? ¿Cuánto tiempo duraría la duración del día?
Estrategia
Usando la ecuación 10.3, podemos establecer el peso aparente ($F_s$) en cero y determinar la aceleración centrípeta requerida. A partir de ello, podemos encontrar la velocidad en el ecuador. La duración del día es el tiempo requerido para una rotación completa.
Solución
De la Ecuación 10.2, tenemos $\sum F = F_s -mg = ma_c$, por lo que al establecer $F_s = 0$, obtenemos $g = a_c$. Usando la expresión para $a_c$, sustituyendo el radio de la Tierra y el valor estándar de la gravedad, obtenemos
$$a_c = \frac{v^2}{r}$$ $$\begin{split} v &= \sqrt{gr}\\ &= \sqrt{(9.80 m/s^2)(6.37 \times 10^6 m)}\\ &= 7.91 \times 10^6 m/s \end{split}$$El período $T$ es el tiempo para una rotación completa. Por lo tanto, la velocidad tangencial es la circunferencia dividida por $T$, por lo que tenemos:
Explicación
Veremos más adelante en este capítulo que esta velocidad y duración del día también sería la velocidad orbital y el período de un satélite en órbita en la superficie de la Tierra. Si bien esa órbita no sería posible cerca de la superficie de la Tierra debido a la resistencia del aire, ciertamente es posible solo a unos pocos cientos de millas sobre la Tierra.
Resultados lejos del ecuador
En los polos, $a_c \to 0$ y $F_s = mg$, tal como es el caso sin rotación. En cualquier otra latitud $\lambda$, la situación es más complicada. La aceleración centrípeta se dirige hacia el punto $P$ en la figura, y el radio se convierte en $r = R_Ecos\lambda$. La suma vectorial del peso y $\bold{\vec{F}}_s$ deben apuntar hacia el punto $P$, por lo tanto, $\bold{\vec{F}}_s$ ya no apunta hacia el centro de la Tierra (La diferencia es pequeña y exagerada en la figura). Una plomada siempre apuntará a lo largo de esta dirección desviada. Todos los edificios están construidos alineados a lo largo de esta dirección desviada, no a lo largo de un radio que atraviesa el centro de la Tierra. Para los edificios más altos, esto representa una desviación de unos pocos pies en la parte superior.
También vale la pena señalar que la Tierra no es una esfera perfecta.
El interior es parcialmente líquido, y esto mejora el abultamiento de la Tierra en el ecuador debido a su rotación.
El radio de la Tierra es aproximadamente $30 km$ mayor en el ecuador en comparación con los polos. Se deja como ejercicio el comparar la fuerza de la gravedad en los polos con la del ecuador usando la Ecuación 10.2. La diferencia es comparable a la diferencia debida a la rotación y está en la misma dirección. Aparentemente, puedes perder "peso" al mudarte a los trópicos.
Gravedad lejos de la superficie
Anteriormente afirmamos sin pruebas que la ley de la gravitación se aplica a los objetos esféricamente simétricos, donde la masa de cada cuerpo actúa como si estuviera en el centro del cuerpo. Como la Ecuación 10.2 se deriva de la Ecuación 10.1, también es válida para distribuciones de masa simétricas, pero ambas ecuaciones son válidas solo para valores de $r \ge R_E$. Como vimos en el Ejemplo 10.4, a $400 km$ sobre la superficie de la Tierra, donde la Estación Espacial Internacional orbita, el valor de $g$ es $8.67 m/s^2$ (Veremos más adelante que esta es también la aceleración centrípeta de la EEI).
Para $r \lt R_E$, las ecuaciones 10.1 y 10.2 no son válidas. Sin embargo, podemos determinar g para estos casos usando un principio que proviene de la ley de Gauss, que es una poderosa herramienta matemática que estudiaremos con más detalle más adelante. Una consecuencia de la ley de Gauss, aplicada a la gravitación, es que solo la masa dentro de $r$ contribuye a la fuerza gravitatoria. Además, esa masa, al igual que antes, puede considerarse ubicada en el centro. El efecto gravitacional de la masa fuera de r tiene un efecto neto cero.
Dos casos especiales muy interesantes ocurren.
Para un planeta esférico con densidad constante, la masa dentro de $r$ es la densidad multiplicada por el volumen dentro de $r$.
Esta masa se puede considerar ubicada en el centro.
Sustituyendo $M_E$ con solo la masa dentro de $r$ por $M = \rho \times (\text{volumen de una esfera})$, y $R_E$ por $r$, la ecuación 10.2 se vuelve
$$g = G\frac{M_E}{R_E^2} = G\frac{\rho(4/3πr^3)}{r^2} = \frac43 G\rho \pi r$$El valor de $g$, y por lo tanto su peso, disminuye linealmente a medida que desciende por un agujero hasta el centro del planeta esférico. En el centro, es ingrávida, ya que la masa del planeta tira por igual en todas las direcciones.
En realidad, la densidad de la Tierra no es constante, ni la Tierra es sólida en todas partes. La Figura 10.10 muestra el perfil de $g$ si la Tierra tiene densidad constante y el perfil más probable se basa en las estimaciones de densidad derivadas de los datos sísmicos.
El segundo caso interesante se refiere a vivir en un planeta de corteza esférica. Este escenario ha sido propuesto en muchas historias de ciencia ficción. Ignorando los problemas de ingeniería significativos, la corteza podría construirse con un radio deseado y una masa total, tal que $g$ en la superficie sea el mismo que el de la Tierra.
¿Puedes adivinar qué pasa una vez que desciendes en un ascensor hacia el interior de la corteza, donde no hay masa entre tú y el centro? ¿Qué beneficios proporcionaría esto para viajar grandes distancias desde un punto en la esfera a otro? Y finalmente, ¿qué efecto habría si el planeta girara?
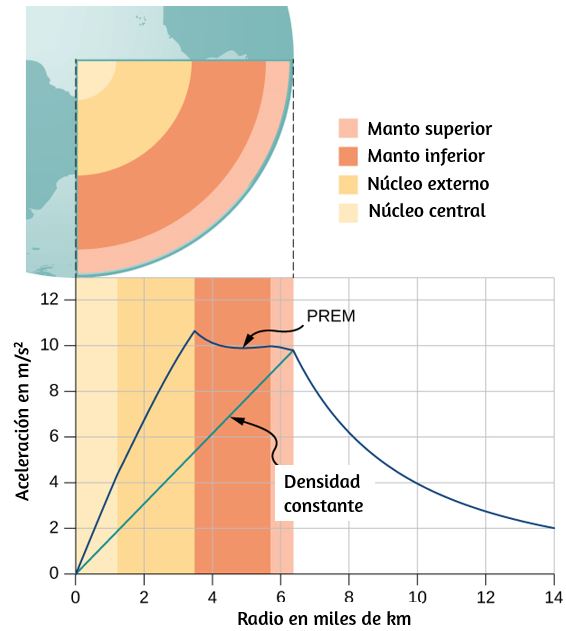
Energía potencial gravitacional y energía total
Estudiamos la energía potencial gravitacional en el capítulo "Energía potencial y Conservación de la energía", donde el valor de $g$ se mantuvo constante. Ahora desarrollaremos una expresión que funciona a distancias tales que g no es constante.
Energía potencial gravitacional más allá de la Tierra
Hemos definido el trabajo y la energía potencial. La utilidad de esas definiciones es la facilidad con la que podemos resolver muchos problemas utilizando la conservación de la energía. La energía potencial es particularmente útil para las fuerzas que cambian con la posición, ya que la fuerza gravitatoria lo hace a grandes distancias. Demostramos, también, que el cambio en la energía potencial gravitacional cerca de la superficie de la Tierra es $\Delta U = mg(y_2 - y_1)$. Esto funciona muy bien si $g$ no cambia significativamente entre $y_1$ e $y_2$. Volvemos a la definición de trabajo y energía potencial para derivar una expresión que es correcta a grandes distancias.
Recuerda que el trabajo ($W$) es la integral del producto escalar entre la fuerza y la distancia. Esencialmente, es el producto del componente de una fuerza a lo largo de un desplazamiento multiplicado por ese desplazamiento. Definimos $\Delta U$ como el negativo del trabajo realizado por la fuerza que asociamos con la energía potencial. Para mayor claridad, derivamos una expresión para mover una masa m desde la distancia $r_1$ desde el centro de la Tierra hasta la distancia $r_2$. Sin embargo, el resultado se puede generalizar fácilmente a dos objetos que cambian su separación de un valor a otro.
Considera la Figura 10.11, en la cual tomamos $m$ desde una distancia $r_1$ desde el centro de la Tierra hasta una distancia que es $r_2$ desde el centro. La gravedad es una fuerza conservadora (su magnitud y dirección son funciones de la ubicación solamente), por lo que podemos tomar cualquier trayectoria que deseemos, y el resultado para el cálculo del trabajo es el mismo.

Tomamos la trayectoria que se muestra en la figura, ya que simplifica enormemente la integración. Primero nos movemos radialmente hacia afuera desde la distancia $r_1$ a la distancia $r_2$, y luego nos movemos a lo largo del arco de un círculo hasta que alcanzamos la posición final. Durante la porción radial, $\bold{\vec{F}}$ es opuesta a la dirección en que viajamos a lo largo de $d\bold{\vec{r}}$, así que $E = K_1 + U_1 = K_2 + U_2$. A lo largo del arco, $\bold{\vec{F}}$ es perpendicular a $d\bold{\vec{r}}$, entonces $\bold{\vec{F}}\cdot d\bold{\vec{r}} = 0$. No se realiza ningún trabajo mientras avanzamos a lo largo del arco. Usando la expresión de la fuerza gravitacional y observando los valores de $\bold{\vec{F}}\cdot d\bold{\vec{r}}$ a lo largo de los dos segmentos de nuestra trayectoria, tenemos
$$\delta U = −\int_{r_1}^{r_2} \bold{\vec{F}}\cdot d\bold{\vec{r}} = GM_Em\int_{r_1}^{r_2} \frac{dr}{r^2} = = GM_Em\Big(\frac{1}{r_1} - \frac{1}{r_2}\Big)$$Dado que $\Delta U = U_2 - U_1$, podemos adoptar una expresión simple para $U$:
Ten en cuenta dos elementos importantes con esta definición. Primero, $U \to 0$ como $r \to \infin$. La energía potencial es cero cuando las dos masas están infinitamente separadas. Solo la diferencia en $U$ es importante, por lo que la elección de $U = 0$ para $r = \infin$ es meramente de conveniencia (Recuerda que en problemas de gravedad anteriores, eras libre de tomar U = 0 en la parte superior o inferior de un edificio, o en cualquier parte). En segundo lugar, ten en cuenta que $U$ se vuelve cada vez más negativo a medida que las masas se acercan. Eso es consistente con lo que aprendiste sobre la energía potencial.
Como las dos masas están separadas, se debe realizar un trabajo positivo contra la fuerza de la gravedad, y por lo tanto, $U$ aumenta (se vuelve menos negativo). Todas las masas se unen de forma natural bajo la influencia de la gravedad, cayendo desde una energía potencial superior a una inferior.
Ejemplo 10.6
Levantando una carga útil
¿Cuánta energía se necesita para levantar el vehículo Soyuz de $9000 kg$ desde la superficie de la Tierra hasta la altura del ISS, $400 km$ por encima de la superficie?
Estrategia
Usa la ecuación 10.2 para encontrar el cambio en la energía potencial de la carga útil. Esa cantidad de trabajo o energía se debe suministrar para levantar la carga útil.
Solución
Prestando atención al hecho de que comenzamos en la superficie de la Tierra y terminamos a $400 km$ sobre la superficie, el cambio en $U$ es
$$\Delta U = U_{orbit} − U_{Tierra} = - \frac{GM_Em}{R_E + 400 km} - \Big(- \frac{GM_Em}{R_E}\Big)$$Insertamos los valores
$$m = 9000 kg, M_E = 5.96 \times 10^{24} kg,\\ R_E = 6.37 \times 10^6 m$$y conviertes $400 km$ en $4.00 \times 10^5 m$. Encontramos $\Delta U = 3.32 \times 10^{10} J$. Es positivo, lo que indica un aumento en la energía potencial, como era de esperar.
Explicación
Como perspectiva, considera que el uso promedio de energía en los hogares de EE. UU., en 2013, fue de $909 kWh$ por mes. Esa es la energía de
$$909 kWh × 1000W/kW × 3600s/h = 3.27\times 10^9J\;\text{ por mes}$$Entonces, nuestro resultado es un gasto de energía equivalente a $10$ meses. Pero esta es solo la energía necesaria para elevar la carga útil a 400 km.
Si queremos que el Soyuz esté en órbita para que pueda encontrarse con el ISS y no simplemente retroceder a la Tierra, necesita mucha energía cinética. Como vemos en la siguiente sección, esa energía cinética es aproximadamente cinco veces la de ΔU. Además, se gasta mucha más energía levantando el propio sistema de propulsión. Los viajes espaciales no son baratos.
 Comprueba tu aprendizaje 10.2
Comprueba tu aprendizaje 10.2
Conservacion de la energia
En el capítulo de energía potencial y conservación de la energía, describimos cómo aplicar la conservación de energía para sistemas con fuerzas conservadoras. Pudimos resolver muchos problemas, particularmente aquellos que involucran la gravedad, más simplemente usando la conservación de la energía. Esos principios y estrategias de resolución de problemas se aplican igualmente bien aquí. El único cambio es colocar la nueva expresión de energía potencial en la ecuación de conservación de la energía, $E = K_1 + U_1 = K_2 + U_2.
Ten en cuenta que usamos $M$, en lugar de $M_E$, como un recordatorio de que no estamos restringidos a problemas que involucran a la Tierra. Sin embargo, todavía suponemos que $m \lt\lt M $(Para problemas en los que esto no es cierto, necesitamos incluir la energía cinética de ambas masas y usar la conservación del momento para relacionar las velocidades entre sí. Pero el principio sigue siendo el mismo).
Velocidad de escape
La velocidad de escape a menudo se define como la velocidad inicial mínima de un objeto que se requiere para escapar de la superficie de un planeta (o cualquier cuerpo grande como la luna) y nunca regresar. Como de costumbre, suponemos que no se pierde energía en la atmósfera, en caso de haberla.
Considera el caso donde un objeto se lanza desde la superficie de un planeta con una velocidad inicial dirigida lejos del planeta. Con la velocidad mínima necesaria para escapar, el objeto simplemente llegaría a descansar infinitamente lejos, es decir, el objeto cederá el último de su energía cinética justo cuando alcanza el infinito, donde la fuerza de la gravedad se vuelve cero. Desde $U \to 0$ y $r \to infin$, esto significa que la energía total es cero. Por lo tanto, encontramos la velocidad de escape desde la superficie de un cuerpo astronómico de masa $M$ y radio $R$ al establecer la energía total igual a cero. En la superficie del cuerpo, el objeto se encuentra en $r_1 = R$ y tiene una velocidad de escape $v_1 = v_{esc}$. Alcanza $r_2 = \infin$ con velocidad $v_2 = 0$. Sustituyendo a la Ecuación 10.5, tenemos
$$\frac12 mv_{esc}^2 - \frac{GMm}{R} = \frac12 m_0^2 - \frac{GMm}{\infin} = 0$$Resolviendo para la velocidad de escape,
Observa que $m$ se ha cancelado fuera de la ecuación. La velocidad de escape es la misma para todos los objetos, independientemente de la masa. Además, no estamos restringidos a la superficie del planeta; R puede ser cualquier punto de partida más allá de la superficie del planeta.
Ejemplo 10.7
Escapando de la tierra
¿Cuál es la velocidad de escape de la superficie de la Tierra? Supón que no hay pérdida de energía por la resistencia del aire. Compara esto con la velocidad de escape del Sol, comenzando desde la órbita de la Tierra.
Estrategia
Usamos la Ecuación 10.6, que define claramente los valores de $R$ y $M$. Para escapar de la Tierra, necesitamos la masa y el radio de la Tierra. Para escapar del Sol, necesitamos la masa del Sol y la distancia orbital entre la Tierra y el Sol.
Solución
Sustituyendo los valores de la masa y el radio de la Tierra directamente en la Ecuación 10.6, obtenemos
Eso es aproximadamente $11 km/s$ o $25,000 mph$. Para escapar del Sol, comenzando desde la órbita de la Tierra, usamos $R = R_{TS} = 1.50 \times 10^{11}m$ y $M_{sol} = 1.99 \times 10^{30} kg$. El resultado es $v_{esc} = 4.21 \times 10^4 m/s$ o aproximadamente $42 km/s$.
Explicación
La velocidad necesaria para escapar del Sol (salir del sistema solar) es casi cuatro veces la velocidad de escape de la superficie de la Tierra. Pero hay ayuda en ambos casos. La Tierra está girando, a una velocidad de casi de $1,7 km/s$ en el ecuador, y podemos usar esa velocidad para ayudarnos a escapar, o para lograr la órbita.
Por esta razón, muchas compañías espaciales comerciales mantienen instalaciones de lanzamiento cerca del ecuador. Para escapar del Sol, hay aún más ayuda. La Tierra gira alrededor del Sol a una velocidad de aproximadamente $30 km/s$. Al lanzar en la dirección en que la Tierra se está moviendo, solo necesitamos $12 km/s$ adicionales. El uso de la asistencia gravitacional de otros planetas, es esencialmente una técnica de tirachinas de gravedad, permite que las sondas espaciales alcancen velocidades aún mayores. En esta técnica, el vehículo se acerca al planeta y se acelera por la atracción gravitacional del planeta. Tiene su mayor velocidad en el punto más cercano de aproximación, aunque se desacelera en la misma medida a medida que se aleja. Pero en relación con el planeta, la velocidad del vehículo mucho antes de la aproximación, y mucho después, es la misma.
Si las instrucciones se eligen correctamente, eso puede dar como resultado un aumento significativo (o una disminución si es necesario) en la velocidad del vehículo en relación con el resto del sistema solar.
 Comprueba tu aprendizaje 10.4
Comprueba tu aprendizaje 10.4
Energía y objetos gravitacionales
Como se indicó anteriormente, la velocidad de escape se puede definir como la velocidad inicial de un objeto que puede escapar de la superficie de una luna o un planeta. De manera más general, es la velocidad en cualquier posición tal que la energía total es cero. Si la energía total es cero o mayor, el objeto se escapa. Si la energía total es negativa, el objeto no puede escapar. Veamos por qué ese es el caso.
Como se señaló anteriormente, vemos que $U \to 0$ si $r \to \infin$. Si la energía total es cero, entonces cuando m alcanza un valor de $r$ que se acerca al infinito, $U$ se convierte en cero y también la energía cinética. Por lo tanto, m se detiene infinitamente lejos de $M$. Se "acaba de escapar" $M$. Si la energía total es positiva, entonces la energía cinética permanece en $r = \infin$ y ciertamente m no regresa. Cuando la energía total es cero o mayor, decimos que $m$ no está unida gravitacionalmente a $M$.
Por otro lado, si la energía total es negativa, entonces la energía cinética debe llegar a cero en algún valor finito de $r$, donde $U$ es negativo e igual a la energía total.
El objeto nunca puede exceder esta distancia finita de $M$, ya que hacerlo requeriría que la energía cinética se vuelva negativa, lo cual no es posible. Decimos que $m$ está gravitacionalmente ligado a M.
Hemos simplificado esta discusión asumiendo que el objeto se dirigió directamente fuera del planeta. Lo que es notable es que el resultado se aplica a cualquier velocidad. La energía es una cantidad escalar y, por lo tanto, la ecuación 10.5 es una ecuación escalar: la dirección de la velocidad no juega ningún papel en la conservación de la energía. Es posible tener un sistema gravitacionalmente ligado donde las masas no "caigan juntas", sino que mantengan un movimiento orbital el uno sobre el otro.
Tenemos una observación final importante. Anteriormente afirmamos que si la energía total es cero o mayor, el objeto se escapa. Estrictamente hablando, las ecuaciones 10.5 y 10.6 se aplican a los objetos puntuales. También se aplican a objetos de tamaño finito, esféricamente simétricos, siempre que el valor de r en la Ecuación 10.5 sea siempre mayor que la suma de los radios de los dos objetos.
Si $r$ es menor que esta suma, entonces los objetos colisionan (Incluso para valores mayores de $r$, pero cerca de la suma de los radios, las fuerzas mareales gravitacionales podrían crear efectos significativos si ambos objetos son de tamaño planetario.
Examinamos los efectos de las mareas). Ni la energía total positiva ni negativa impide masas de tamaño finito de colisionar. Para objetos reales, la dirección es importante.
Ejemplo 10.8
¿Hasta dónde puede escapar un objeto?
Consideremos nuevamente el ejemplo anterior, donde calculamos la velocidad de escape desde la Tierra y el Sol, comenzando desde la órbita de la Tierra. Notamos que la Tierra ya tiene una velocidad orbital de $30 km/s$. Como veremos en la siguiente sección, esa es la velocidad tangencial necesaria para permanecer en órbita circular. Si un objeto tenía esta velocidad a la distancia de la órbita de la Tierra, pero se dirigía directamente lejos del Sol, ¿qué tan lejos viajaría antes de detenerse? Ignora los efectos gravitacionales de otros cuerpos.
Estrategia
El objeto tiene energías cinéticas y potenciales iniciales que podemos calcular. Cuando su velocidad llega a cero, está a su distancia máxima del Sol. Usamos la ecuación 10.5, conservación de la energía, para encontrar la distancia a la que la energía cinética es cero.
Solución
La posición inicial del objeto es el radio de órbita de la Tierra y la velocidad inicial se da como $30 km/s$. La velocidad final es cero, por lo que podemos hallar la distancia en ese punto desde la ecuación de la conservación de la energía. Utilizando $R_{TS} = 1.50 \times 10^{11} m$ y $M_{sol} = 1.99 \times 10^{30} kg$, tenemos
$$\frac12 mv_1^2 - \frac{GMm}{r_1} = \frac12 mv_2^2 - \frac{GMm}{r_2}$$reemplazando
donde la masa $m$ se cancela. Resolviendo para $r_2$ obtenemos $r_2 = 3.0 \times 10^{11} m$. Ten en cuenta que esto es dos veces la distancia inicial del Sol y nos lleva más allá de la órbita de Marte, pero no del cinturón de asteroides.
Explicación
El objeto en este caso alcanzó una distancia exactamente el doble de la distancia orbital inicial. Veremos la razón de esto en la próxima sección cuando calculemos la velocidad de las órbitas circulares.
 Comprueba tu aprendizaje 10.5
Comprueba tu aprendizaje 10.5
En el siguiente objeto interactivo de PhET Explorations, mueve el sol, la tierra, la luna y la estación espacial para ver cómo afecta sus fuerzas gravitatorias y trayectorias orbitales. ¡Visualiza los tamaños y las distancias entre los diferentes cuerpos celestes y desactiva la gravedad para ver lo que pasaría sin ésta!.
Órbitas satelitales y energía
La Luna orbita la Tierra. A su vez, la Tierra y los otros planetas orbitan alrededor del Sol. El espacio directamente sobre nuestra atmósfera está lleno de satélites artificiales en órbita. Examinaremos la órbita más simple de estas, la órbita circular, para comprender la relación entre la velocidad y el período de los planetas y los satélites en relación con sus posiciones y los cuerpos que orbitan.
Órbitas circulares
Como se señaló al principio de este capítulo, Nicolaus Copérnico sugirió por primera vez que la Tierra y todos los demás planetas orbitan alrededor del Sol en círculos.
Señaló además que los períodos orbitales aumentaron con la distancia del sol. El análisis posterior de Kepler mostró que estas órbitas son en realidad elipses, pero las órbitas de la mayoría de los planetas del sistema solar son casi circulares. La distancia orbital de la Tierra desde el Sol varía solo un $2\%$. La excepción es la órbita excéntrica de Mercurio, cuya distancia orbital varía casi $40\%$.
La determinación de la velocidad orbital y el período orbital de un satélite es mucho más fácil para las órbitas circulares, por lo que hacemos esa suposición en la derivación que sigue. Como describimos en la sección anterior, un objeto con energía total negativa está ligado gravitacionalmente y, por lo tanto, está en órbita. Nuestro cálculo para el caso especial de órbitas circulares lo confirmará. Nos enfocamos en objetos que orbitan alrededor de la Tierra, pero nuestros resultados pueden generalizarse para otros casos.
Considera un satélite de masa $m$ en una órbita circular alrededor de la Tierra a una distancia r del centro de la Tierra (Figura 10.12).
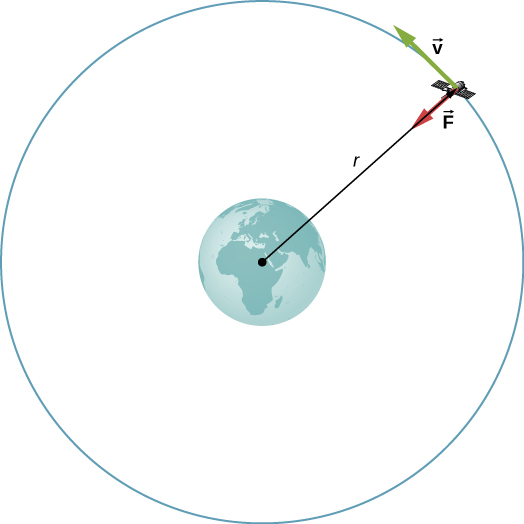
Tiene aceleración centrípeta dirigida hacia el centro de la Tierra. La gravedad de la Tierra es la única fuerza que actúa, por lo que la segunda ley de Newton nos da
$$\frac{GmM_E}{r^2} = ma_c = \frac{mv_{orbit}^2}{r}$$De acuerdo con lo que vimos en las ecuaciones 10.2 y 10.6, m no aparece en la ecuación 10.7. El valor de $g$, la velocidad de escape y la velocidad orbital dependen solo de la distancia desde el centro del planeta, y no de la masa del objeto sobre el que se actúa. Observa la similitud en las ecuaciones para $v_{orbit}$ y $v_{esc}$. La velocidad de escape es exactamente $2$ veces mayor, aproximadamente $40\%$, que la velocidad orbital. Esta comparación se observó en el Ejemplo 10.7, y es verdadera para un satélite en cualquier radio.
Para encontrar el período de una órbita circular, notamos que el satélite recorre la circunferencia de la órbita $2\pi r$ en un período $T$. Usando la definición de velocidad, tenemos $v_{orbit} = 2\pi r / T$. Sustituimos esto en la Ecuación 10.7 y reorganizamos para obtener
Vemos en la siguiente sección que esto representa la tercera ley de Kepler para el caso de las órbitas circulares.
También confirma la observación de Copérnico de que el período de un planeta aumenta al aumentar la distancia del Sol.
Solo necesitamos reemplazar $M_E$ con $M_{Sol}$ en la Ecuación 10.8.
Concluimos esta sección volviendo a nuestra discusión anterior sobre los astronautas en órbita que parecen no tener peso, como si estuvieran cayendo libremente hacia la Tierra. De hecho, están en caída libre. Considera las trayectorias que se muestran en la figura 10.13 (Esta figura se basa en un dibujo de Newton en su Principia). Todas las trayectorias que se muestran que golpean la superficie de la Tierra tienen una velocidad inferior a la orbital. Los astronautas acelerarían hacia la Tierra a lo largo de las trayectorias no circulares que se muestran y se sentirían sin peso (Los astronautas realmente entrenan para vivir en órbita montando en aviones que caen libremente durante $30$ segundos a la vez). Pero con la velocidad orbital correcta, la superficie de la Tierra se aleja de ellos exactamente a la misma velocidad con la que caen hacia la Tierra. Por supuesto, mantenerse a la misma distancia de la superficie es el punto de una órbita circular.
Podemos resumir nuestra discusión sobre los satélites en órbita en la siguiente Estrategia de resolución de problemas.
1. Determina si las ecuaciones de velocidad, energía o período son válidas para el problema en cuestión. Si no, comienza con los primeros principios que usamos para derivar esas ecuaciones.
3. Junto con las definiciones de velocidad y energía, aplica la segunda ley del movimiento de Newton a los cuerpos de interés.
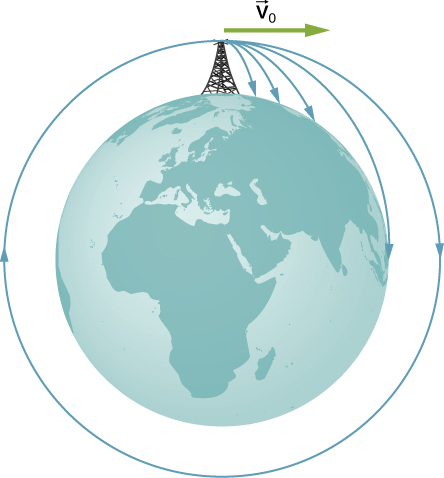
Ejemplo 10.9
La Estación Espacial Internacional
Determina la velocidad orbital y el período de la Estación Espacial Internacional (ISS).
Estrategia
Dado que el ISS orbita a $4.00 \times 10^2 km$ sobre la superficie de la Tierra, el radio en el que orbita es $R_E + 4.00 \times 10^2 km$. Usamos las ecuaciones 10.7 y 10.8 para encontrar la velocidad y el período orbitales, respectivamente.
Solución
Usando la ecuación 10.7, la velocidad orbital es
$$\begin{split} v_{orbit} &= \sqrt{\frac{GM_E}{r}}\\ &= \frac{6.67\times 10^{-11} N\cdot m^2/kg^2 (5.96\times 10^{24} kg}{6.36\times 10^6 + 4.00\times 10^5m)}\\ &= 7.67\times 10^3 m/s \end{split}$$que es aproximadamente $17,000 mph.$ Usando la ecuación 10.8, el período es
$$\begin{split} T &= 2\pi \sqrt{\frac{r^3}{GM_E}} = 2\pi \sqrt{\frac{(6.67\times 10^6 + 4.00\times 10^5m)^3}{6.67\times 10^{-11} N\cdot m^2/kg^2)(5.96\times 10^{24}kg)}}\\ &= 5.55\times 10^3 s \end{split}$$que es un poco más de 90 minutos.
Explicación
Se considera que el ISS se encuentra en órbita terrestre baja (LEO). Casi todos los satélites están en LEO, incluida la mayoría de los satélites meteorológicos. Los satélites GPS, a unos $20,000 km$, se consideran una órbita media de la Tierra.
Cuanto más elevada es la órbita, más energía se necesita para ponerla allí y se necesita más energía para llegar a ella para su reparación. De particular interés son los satélites en órbita geosincrónica. Todas las antenas parabólicas fijas en el suelo apuntando hacia el cielo, como los platos de recepción de TV, apuntan hacia satélites geosincrónicos. Estos satélites se colocan a la distancia exacta, y justo encima del ecuador, de modo que su período de órbita es de 1 día. Permanecen en una posición fija con respecto a la superficie de la Tierra.
 Comprueba tu aprendizaje 10.6
Comprueba tu aprendizaje 10.6
Ejemplo 10.10
Determinando la Masa de la Tierra
Determina la masa de la Tierra desde la órbita de la Luna.
Estrategia
Usamos la ecuación 10.8, resolvemos para $M_E$ y sustituimos el período y el radio de la órbita. El radio y el período de la órbita lunar se midieron con una precisión razonable hace miles de años. A partir de datos astronómicos, el período de la Luna es de $27,3 \;días = 2,36 \times 10^6 s$, y la distancia promedio entre los centros de la Tierra y la Luna es de $384,000 km$.
Solución
Resolviendo para $M_E, T = 2\pi \sqrt{r^3/GM_E}$
$$\begin{split} M_E &= \frac{4\pi ^2r^3}{GT^2}\\ &= \frac{4\pi ^2(3.84 \times 10^8 m)^2}{(6.67 \times 10^{-11} N\cdot m^2/kg^2)(2.36 \times 10^6 m)^2}\\ &= 6.01 \times 10^{24} kg \end{split}$$Explicación
Compara esto con el valor de $5.96 \times 10^{24} kg$ que obtuvimos en el Ejemplo 10.5, usando el valor de g en la superficie de la Tierra. Aunque estos valores son muy cercanos ($\approx 0.8\%$), ambos cálculos usan valores promedio. El valor de $g$ varía desde el ecuador hasta los polos en aproximadamente $0.5\%$. Pero la Luna tiene una órbita elíptica en la que el valor de $r$ varía un poco más del $10\%$ (El tamaño aparente de la Luna llena, en realidad varía aproximadamente en esta cantidad, pero es difícil de notar por observación casual ya que el tiempo de un extremo al otro es de muchos meses).
 Comprueba tu aprendizaje 10.7
Comprueba tu aprendizaje 10.7
Ejemplo 10.11
Velocidad y período galáctico
Revisemos el Ejemplo 10.2. Supongamos que la Vía Láctea y las galaxias de Andrómeda están en órbita circular una sobre la otra. ¿Cuál sería la velocidad de cada una y por cuánto tiempo sería su período orbital? Supongamos que la masa de cada una es de $800$ mil millones de masas solares y sus centros están separados por $2,5$ millones de años luz.
Estrategia
No podemos usar las Ecuaciones 10.7 y 10.8 directamente porque se derivaron suponiendo que el objeto de masa m orbitaba alrededor del centro de un planeta de masa $M$ más grande. Determinamos la fuerza gravitacional en el Ejemplo 10.2 usando la ley de gravitación universal de Newton. Podemos usar la segunda ley de Newton, aplicada a la aceleración centrípeta de cualquiera de las galaxias, para determinar su velocidad tangencial. De ese resultado podemos determinar el período de la órbita.
Solución
En el ejemplo 10.2, encontramos que la fuerza entre las galaxias era
$$\bold{\vec{F}}_{12} = Gm_1m_2r^2 = (6.67 × 10^{−11} N\cdot m^2/kg^2)$$y que la aceleración de cada galaxia es
$$a = \frac{F}{m} = \frac{3.0 \times 10^{29} N}{(800 \times 10^9)(2.0 \times 10^{30} kg)} = 1.9 \times 10^{-13}> m/s^2$$Como las galaxias están en una órbita circular, tienen aceleración centrípeta. Si ignoramos el efecto de otras galaxias, entonces, como aprendimos antes, los centros de masa de las dos galaxias permanecen fijos. Por lo tanto, las galaxias deben orbitar alrededor de este centro común de masa. Para masas iguales, el centro de masa está exactamente a mitad de camino entre ellos. Entonces el radio de la órbita, $r_{orbit}$, no es lo mismo que la distancia entre las galaxias, sino la mitad de ese valor, o $1.25$ millones de años luz. Estos dos valores diferentes se muestran en la figura 10.14.

Usando la expresión para la aceleración centrípeta, tenemos
$$a_c =\frac{v_{orbit}}{r_{orbit}}$$ $$1.9 \times 10^{−13}m/s^2\frac{v_{orbit}^2}{(1.25 \times 10^6)(9.5 \times 10^{15} m)}$$Resolviendo para la velocidad de la órbita, tenemos $v_{orbit} = 47 km/s$. Finalmente, podemos determinar el período de la órbita directamente desde $T = 2πr/v_{orbit}$, para encontrar que el período es $T = 1.6 \times 10^{18} s$, alrededor de $50$ mil millones de años.
Explicación
La velocidad orbital de $47 km/s$ puede parecer alta al principio. Pero esta velocidad es comparable a la velocidad de escape del Sol, que calculamos en un ejemplo anterior. Para dar aún más perspectiva, este período es casi cuatro veces más largo que el tiempo que el Universo ha estado en existencia. De hecho, el movimiento relativo actual de estas dos galaxias es tal que se espera que colisionen en unos 4 mil millones de años. Aunque la densidad de las estrellas en cada galaxia hace poco probable una colisión directa de dos estrellas cualquiera, dicha colisión tendrá un efecto dramático en la forma de las galaxias. Ejemplos de tales colisiones son bien conocidos en astronomía
 Comprueba tu aprendizaje 10.8
Comprueba tu aprendizaje 10.8
Energía en órbitas circulares
Anteriormente, hemos argumentado que los objetos están gravitacionalmente ligados si su energía total es negativa. El argumento se basó en el caso simple donde la velocidad estaba directamente lejos o hacia el planeta. Ahora examinamos la energía total para una órbita circular y mostramos que, de hecho, la energía total es negativa. Como lo hicimos antes, comenzamos con la segunda ley de Newton aplicada a una órbita circular,
$$\frac{GmM_E}{r^2} = m_a = \frac{mv^2}{r}$$ $$\frac{GmM_E}{r} = mv^2$$En el último paso, multiplicamos por r en cada lado. El lado derecho es solo el doble de la energía cinética, entonces tenemos
$$K = \frac12 mv^2 = \frac{GmM_E}{2r}$$La energía total es la suma de las energías cinética y potencial, por lo que nuestro resultado final es
Podemos ver que la energía total es negativa, con la misma magnitud que la energía cinética. Para órbitas circulares, la magnitud de la energía cinética es exactamente la mitad de la magnitud de la energía potencial.
Sorprendentemente, este resultado se aplica a cualquier dos masas en órbitas circulares sobre su centro de masa común, a una distancia r una de la otra. La prueba de esto se deja como un ejercicio. Veremos en la siguiente sección que se aplica una expresión muy similar en el caso de las órbitas elípticas.
Ejemplo 10.12
Energía requerida para orbitar
En el ejemplo 10.8, calculamos la energía requerida para simplemente levantar el vehículo Soyuz de $9000 kg $ desde la superficie de la Tierra hasta la altura del ISS, $400 km$ por encima de la superficie. En otras palabras, encontramos su cambio en la energía potencial.
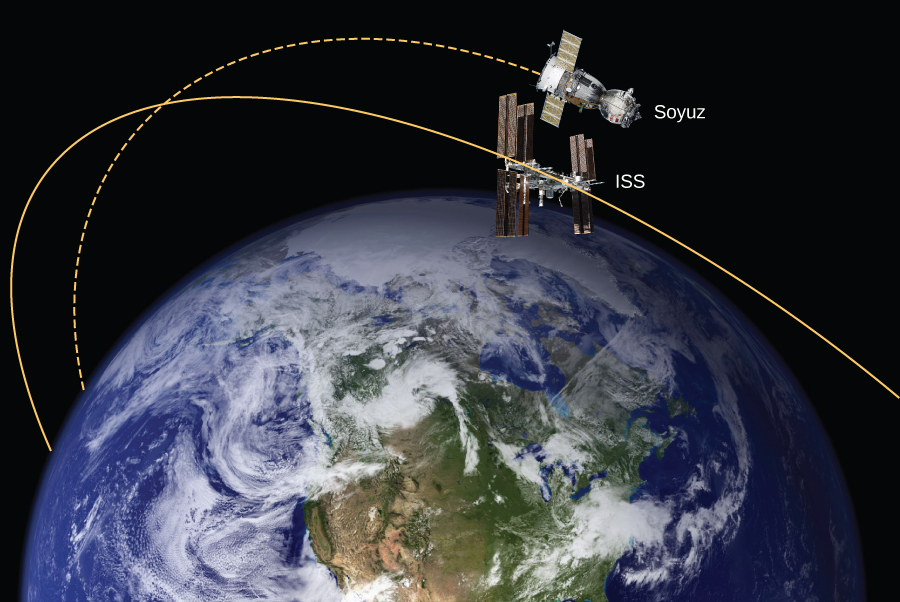
Ahora nos preguntamos, ¿qué cambio total de energía en el vehículo Soyuz se requiere para sacarlo de la superficie de la Tierra y ponerlo en órbita con el ISS para una reunión espacial (Figura 10.15)? ¿Cuánto de esa energía total es energía cinética?
Estrategia
La energía requerida es la diferencia en la energía total del Soyuz en órbita y en la superficie de la Tierra. Podemos usar la Ecuación 10.9 para encontrar la energía total del Soyuz en la órbita de ISS. Pero la energía total en la superficie es simplemente la energía potencial, ya que comienza desde el reposo (Ten en cuenta que no utilizamos la ecuación 10.9 en la superficie, ya que no estamos en órbita en la superficie). La energía cinética se puede encontrar a partir de la diferencia en el cambio de energía total y el cambio en la energía potencial que se encuentra en el ejemplo 10.8. Alternativamente, podemos usar la Ecuación 10.7 para encontrar $v_{orbit}$ y calcular la energía cinética directamente a partir de eso. La energía total requerida es entonces la energía cinética más el cambio en la energía potencial que se encuentra en el Ejemplo 10.8.
Solución
De la Ecuación 10.9, la energía total del Soyuz en la misma órbita que la ISS es
$$\begin{split} E_{orbit} &= K_{orbit} + U_{orbit}\\ &= −\frac{GmM_E}{2r}\\ &= -\frac{(6.67 \times 10^{−11} N\cdot m^2/kg^2)(9000 kg)(5.96 \times 10^{24} kg)}{(6.36 \times 10^6 m)}\\ &= −5.63 \times 10^{11} J \end{split}$$El cambio en la energía es $\Delta E = E_{orbit} -E_{superficie} = 2.98 \times 10^{11} J$. Para obtener la energía cinética, restamos el cambio en la energía potencial del ejemplo 10.6, $\Delta U = 3.32 \times 10^{10} J$.
Eso nos da $K_{orbit} = 2.98 \times 10^{11} - 3.32 \times 10^{10} = 2.65 \times 10^{11} J$. Como se dijo anteriormente, la energía cinética de una órbita circular es siempre la mitad de la magnitud de la energía potencial, y lo mismo que la magnitud de la energía total. Nuestro resultado confirma esto.
El segundo enfoque es usar la Ecuación 10.7 para encontrar la velocidad orbital del Soyuz, lo cual hicimos para la ISS en el Ejemplo 10.9.
$$\begin{split} v_{orbit} &= \sqrt{\frac{GM_E}{r}}\\ &= \sqrt{\frac{(6.67\times 10^{-11} N\cdot m^2/kg^2)(5.96 \times 10^{24} kg)}{(6.36 \times 10^6 + 4.00\times 10^5 m)}}\\ &= 7.67\times 10^3 m/s \end{split}$$Entonces la energía cinética del Soyuz en órbita es
$$K_{orbit} = \frac12 mv_{orbit}^2 = \frac12 (9000 kg)(7.67 \times 10^3 m/s)^2\\ = 2.65 \times 10^{11} J$$lo mismo que en el método anterior. La energía total es solo
$$E_{orbit} = K_{orbit} + \Delta U = 2,65 \times 10^{11} + 3,32 \times 10^{10}\\ = 2,95 \times 10^{11}J$$Explicación
La energía cinética del Soyuz es casi ocho veces el cambio en su energía potencial, o el $90\%$ de la energía total necesaria para el encuentro con la ISS. Y es importante recordar que esta energía representa solo la energía que se le debe dar al Soyuz.
Con nuestra tecnología de cohetes actual, la masa del sistema de propulsión (el combustible del cohete, su contenedor y el sistema de combustión) excede por mucho la de la carga útil, y se debe dar una gran cantidad de energía cinética a esa masa. Entonces, el costo real en energía es muchas veces el del cambio en la energía de la carga útil en sí.
Las leyes de movimiento planetario de Kepler
Usando los datos precisos recopilados por Tycho Brahe, Johannes Kepler analizó cuidadosamente las posiciones en el cielo de todos los planetas conocidos y la Luna, trazando sus posiciones a intervalos regulares de tiempo. A partir de este análisis, formuló tres leyes, que abordamos en esta sección.
La primera ley de Kepler
La visión predominante durante la época de Kepler era que todas las órbitas planetarias eran circulares. Los datos de Marte presentaron el mayor desafío para este punto de vista y finalmente alentaron a Kepler a renunciar a la idea popular. La primera ley de Kepler establece que cada planeta se mueve a lo largo de una elipse, con el Sol ubicado en un foco de la elipse. Una elipse se define como el conjunto de todos los puntos, de modo que la suma de la distancia de cada punto a dos focos es una constante. La figura 10.16 muestra una elipse y describe una forma simple de crearla.
Para las órbitas elípticas, el punto de acercamiento más cercano de un planeta al Sol se llama perihelio. Se denomina punto $A$ en la figura 10.16. El punto más alejado es el afelio y se denomina punto $B$ en la figura. Para la órbita de la Luna sobre la Tierra, esos puntos se llaman perigeo y apogeo, respectivamente.
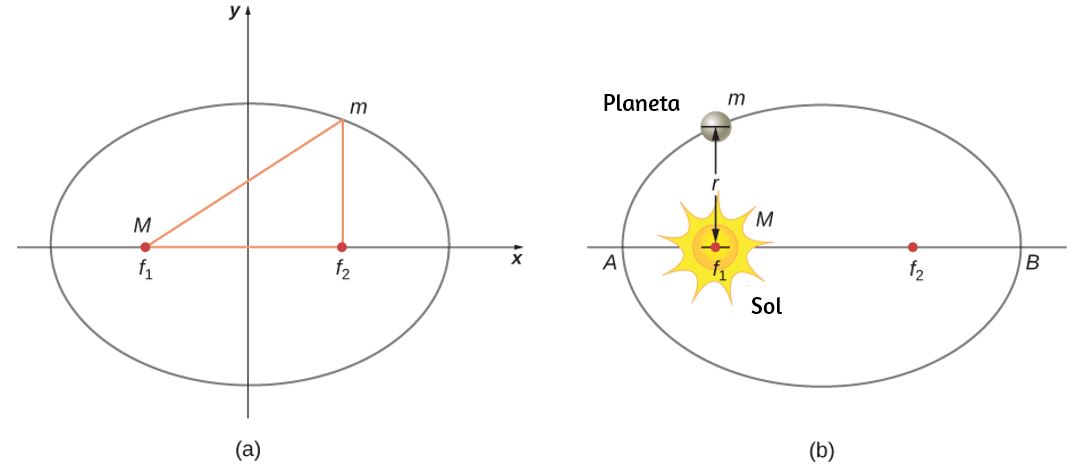
Una elipse tiene varias formas matemáticas, pero todas son un caso específico de la ecuación más general para las secciones cónicas. Hay cuatro secciones cónicas diferentes, todas dadas por la ecuación
Las variables $r$ y $\theta$ se muestran en la figura 10.17 en el caso de una elipse. Las constantes α y e están determinadas por la energía total y el momento angular del satélite en un punto dado. La constante $e$ se llama excentricidad. Los valores de $\alpha$ y $e$ determinan cuál de las cuatro secciones cónicas representa la ruta del satélite.
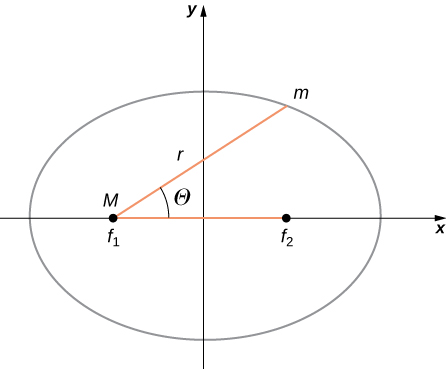
Uno de los verdaderos triunfos de la ley de gravitación universal de Newton, con la fuerza proporcional a la inversa de la distancia al cuadrado, es que cuando se combina con su segunda ley, la solución para la trayectoria de cualquier satélite es una sección cónica. Cada trayectoria tomada por m es una de las cuatro secciones cónicas: un círculo o una elipse para órbitas unidas o cerradas, o una parábola o hipérbola para órbitas ilimitadas o abiertas. Estas secciones cónicas se muestran en la figura 10.18.
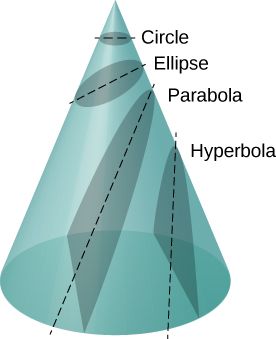
Si la energía total es negativa, entonces $0 \le e \lt 1$, y la ecuación 10.10 representa una órbita unida o cerrada de una elipse o un círculo, donde $e = 0$ (Puedes ver a partir de la ecuación 10.10 que para $e = 0, r = \alpha$, y por lo tanto el radio es constante). Para las elipses, la excentricidad se relaciona con la forma oblonga en que aparece la elipse. Un círculo tiene una excentricidad cero, mientras que una elipse muy larga y alargada tiene una excentricidad cerca de uno.
Si la energía total es exactamente cero, entonces $e = 1$ y la trayectoria es una parábola. Recuerda que un satélite con cero energía total tiene exactamente la velocidad de escape (la parábola se forma solo cortando el cono paralelo a la línea tangente a lo largo de la superficie). Finalmente, si la energía total es positiva, entonces $e \gt 1$ y la trayectoria es una hipérbola.
Estas dos últimas trayectorias representan órbitas ilimitadas, donde m pasa por M una sola vez. Esta situación se ha observado para varios cometas que se acercan al Sol y luego viajan lejos, para nunca regresar.
Nos hemos limitado al caso en que la masa más pequeña (planeta) orbita una masa mucho más grande, y por lo tanto estacionaria, (Sol), pero la Ecuación 10.10 también se aplica a cualquiera dos masas que interactúen gravitatoriamente. Cada masa traza la sección cónica exacta en la misma forma que la otra. Esa forma está determinada por la energía total y el momento angular del sistema, con el centro de masa del sistema ubicado en el foco. La relación de las dimensiones de las dos trayectorias es la inversa de la relación de sus masas.
La siguiente unidad interactiva del Proyecto Un_100, diseñada por José Luis Abreu León, presenta los parámetros que utilizó Kepler para definir una trayectoria elíptica en el espacio, se muestran, además, los valores correspondientes a cada planeta.
En particular se explican los conceptos de equinoxio vernal, período, excentricidad, semieje mayor, perihelio, aelio, longitud de nodo ascendente, longitud de periapsis y anomalía verdadera.
El primer apartado de esta unidad interactiva, con el propósito de motivar el estudio de esta primera Ley de Kepler, presenta extractos de la película Ágora del cineasta Alejandro Amenúbar. En ellos Hipatia se esfuerza en comprender ciertas incongruencias entre las observaciones astronómicas y el modelo heliocéntrico de Aristarco. Como conocía perfectamente las curvas cónicas, la película especula que quizás Hipatia pudo llegar a concebir las trayectorias elípticas, aunque sabemos que quien realmente hizo esto fué Johannes Kepler un milenio más tarde.
Transferencias orbitales
La gente ha imaginado viajar a otros planetas de nuestro sistema solar desde que fueron descubiertos. Pero, ¿cómo podemos hacer mejor esto? El método más eficiente fue descubierto en 1925 por Walter Hohmann, inspirado en una popular novela de ciencia ficción de la época.
El método ahora se llama transferencia de Hohmann. Para el caso de viajar entre dos órbitas circulares, la transferencia se realiza a lo largo de una elipse de "transferencia" que intercepta perfectamente esas órbitas en el afelio y el perihelio de la elipse. La figura 10.19 muestra el caso de un viaje desde la órbita de la Tierra a la de Marte. Como antes, el Sol está en el foco de la elipse.
Para cualquier elipse, el eje semi-mayor se define como la mitad de la suma del perihelio y el afelio. En la figura 10.17, el eje semi mayor es la distancia desde el origen hasta cualquier lado de la elipse a lo largo del eje $x$, o solo la mitad del eje más largo (llamado eje mayor). Por lo tanto, para viajar desde una órbita circular de radio $r_1$ a otra órbita circular de radio $r_2$, el afelio de la elipse de transferencia será igual al valor de la órbita más grande, mientras que el perihelio será la órbita más pequeña. El semi-mayor eje, denotado por $a$, por lo tanto, se da por $a = 12 (r_1 + r_2)$.
Tomemos el caso de viajar de la Tierra a Marte. Por el momento, ignoramos los planetas y suponemos que estamos solos en la órbita de la Tierra y deseamos movernos a la órbita de Marte. De la ecuación 10.9, la expresión de la energía total, podemos ver que la energía total de una nave espacial en la órbita más grande (Marte) es mayor (menos negativa) que la de la órbita más pequeña (la Tierra). Para pasar a la elipse de transferencia desde la órbita de la Tierra, necesitaremos aumentar nuestra energía cinética, es decir, necesitamos un aumento de velocidad.
El método más eficiente es una aceleración muy rápida a lo largo de la trayectoria orbital circular, que también se encuentra a lo largo de la trayectoria de la elipse en ese punto (de hecho, la aceleración debe ser instantánea, de modo que las órbitas circulares y elípticas son congruentes durante la aceleración. En la práctica, la aceleración finita es lo suficientemente corta como para que la diferencia no sea una consideración significativa). Una vez que haya llegado a la órbita de Marte, necesitarás otro aumento de velocidad para moverte a esa órbita, o permanecerás en la órbita elíptica y simplemente volverás al perihelio donde comenzaste.
Para el viaje de regreso, simplemente inviertes el proceso en cada punto de transferencia.
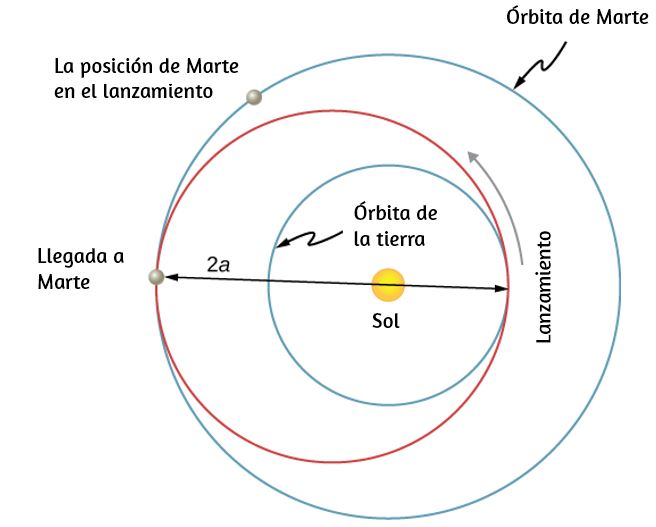
Para hacer el movimiento hacia la elipse de transferencia y luego desactivarlo nuevamente, necesitamos conocer cada velocidad de la órbita circular y las velocidades de la órbita de transferencia en el perihelio y el afelio.
El aumento de velocidad requerido es simplemente la diferencia entre la velocidad de la órbita circular y la velocidad de la órbita elíptica en cada punto. Podemos encontrar las velocidades orbitales circulares de la ecuación 10.7.
Para determinar las velocidades de la elipse, declaramos sin pruebas (ya que está más allá del alcance de este curso) que la energía total para una órbita elíptica es
$$E = -\frac{G_mM_S}{2a}$$donde $M_S$ es la masa del Sol y $a$ es el eje semi-mayor.
Sorprendentemente, esto es lo mismo que la Ecuación 10.9 para órbitas circulares, pero con el valor del eje semi mayor que reemplaza el radio orbital. Como conocemos la energía potencial de la ecuación 10.4, podemos encontrar la energía cinética y, por lo tanto, la velocidad necesaria para cada punto en la elipse. Dejamos que sea un problema de desafío encontrar esas velocidades de transferencia para un viaje de la Tierra a Marte.
Terminamos esta discusión señalando algunos detalles importantes. En primer lugar, no hemos tenido en cuenta la energía potencial gravitatoria debida a la Tierra y Marte, o la mecánica del aterrizaje en Marte. En la práctica, eso debe ser parte de los cálculos. En segundo lugar, el tiempo es todo. No querrás llegar a la órbita de Marte para descubrir que no está allí.
Debemos abandonar la Tierra exactamente en el momento correcto, de modo que Marte esté en el afelio de nuestra elipse de transferencia justo cuando lleguemos. Esa oportunidad se produce cada 2 años. Y regresar también requiere un tiempo correcto. ¡El viaje total tomaría poco menos de $3$ años! Hay otras opciones que proporcionan un tránsito más rápido, incluido un sobrevuelo asistido por gravedad de Venus. Pero estas otras opciones tienen un costo adicional en energía y peligro para los astronautas.
Segunda ley de Kepler
La segunda ley de Kepler establece que un planeta barre áreas iguales en tiempos iguales, es decir, el área dividida por el tiempo, llamada velocidad del área, es constante. Considera la Figura 10.20. El tiempo que le toma a un planeta moverse de la posición $A$ a la $B$, barriendo el área $A_1$, es exactamente el tiempo necesario para pasar de la posición $C$ a la $D$, barrer el área $A_2$ y pasar de $E$ a $F$, barriendo el área $A_3$. Estas áreas son iguales: $A_1 = A_2 = A_3$.
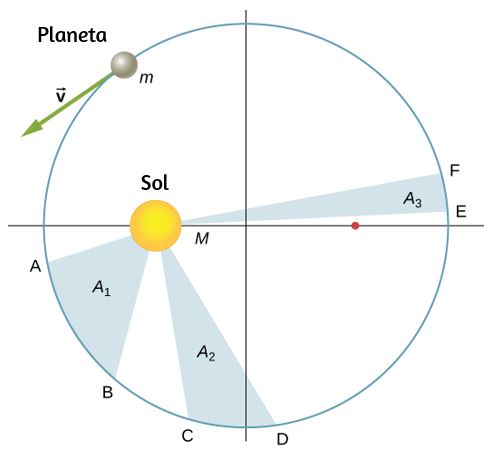
Comparando las áreas en la figura y la distancia recorrida a lo largo de la elipse en cada caso, podemos ver que para que las áreas sean iguales, el planeta debe acelerar a medida que se acerca al Sol y disminuir la velocidad a medida que se aleja. Este comportamiento es completamente coherente con nuestra ecuación de conservación, Ecuación 10.5. Pero demostraremos que la segunda ley de Kepler es en realidad una consecuencia de la conservación del momento angular, que se aplica a cualquier sistema con solo fuerzas radiales.
La definición de momento angular está dada por $\bold{\vec{L}} = \bold{\vec{r}} \times \bold{\vec{p}}$. Para el caso del movimiento en órbita, $\bold{\vec{L}} = \bold{\vec{r}}$ es el momento angular del planeta alrededor del Sol, $\bold{\vec{r}}$ es el vector de posición del planeta medido desde el Sol, y $\bold{\vec{p}} = m\bold{\vec{v}}$ es el momento lineal instantáneo en cualquier punto de la órbita. Como el planeta se mueve a lo largo de la elipse, $\bold{\vec{p}}$ siempre es tangente a la elipse.
Podemos hallar el momento lineal en dos componentes: un componente radial $\bold{\vec{p}}_{rad}$ a lo largo de la línea al Sol, y un componente $\bold{\vec{p}}_{perp}$ perpendicular a $\bold{\vec{r}}$. El producto cruz para el momento angular se puede escribir como
$$\bold{\vec{L}} = \bold{\vec{r}} \times × \bold{\vec{p}} = \bold{\vec{r}} \times (\bold{\vec{p}}_{rad} + \bold{\vec{p}}_{perp}) = \bold{\vec{r}} \times \bold{\vec{p}}_{rad} + \bold{\vec{r}} \times \bold{\vec{p}}_{perp}$$El primer término a la derecha es cero porque $\bold{\vec{r}}$ es paralelo a $\bold{\vec{p}}_{rad}$, y en el segundo término $\bold{\vec{r}}$ es perpendicular a $\bold{\vec{p}}_{perp}$, por lo que la magnitud del producto cruz se reduce a $L = rp_{perp} = rmv_{perp}$. Ten en cuenta que el momento angular no depende de $p_{rad}$. Como la fuerza gravitacional es solo en la dirección radial, solo puede cambiar $p_{rad}$ y no $p_{perp}$; por lo tanto, el momento angular debe permanecer constante.
Ahora considera la figura 10.21. Un área triangular pequeña $\Delta A$ se barre en el tiempo $\Delta t$. La velocidad es a lo largo de la trayectoria y forma un ángulo $\theta$ con la dirección radial. Por lo tanto, la velocidad perpendicular viene dada por $v_{perp} = vsen\theta$. El planeta se mueve una distancia $\Delta s = v\Delta tsen\theta$ proyectado a lo largo de la dirección perpendicular a $r$. Como el área de un triángulo es la mitad de la base ($r$) multiplicada por la altura ($\Delta s$), para un desplazamiento pequeño, el área está dada por $\Delta A = \frac12 r\Delta s$. Sustituyendo $\Delta s$, multiplicando por $m$ en el numerador y el denominador, y reorganizando, obtenemos
$$\begin{split} \Delta A &= \frac12 r\Delta s = \frac12 r(v\Delta tsen\theta) \\ &= \frac{1}{2m}r(mvsen\theta \Delta t) = \frac{1}{2m}r(mv_{perp} \Delta t) \\ &= \frac{L}{2m} \Delta t \end{split}$$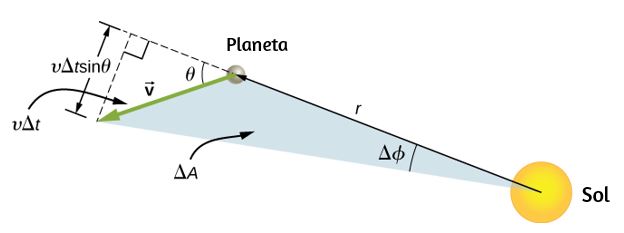
La velocidad del área es simplemente la tasa de cambio del área con el tiempo, por lo que tenemos
Como el momento angular es constante, la velocidad del área también debe ser constante. Esta es exactamente la segunda ley de Kepler. Al igual que con la primera ley de Kepler, Newton demostró que era una consecuencia natural de su ley de gravitación.
La siguiente unidad interactiva del Proyecto Un_100, inicialmente presenta un vídeo dedicado a la vida y obra de Johannes Kepler, en honor a quien descubrió las leyes fundamentales del movimiento planetarios que además llevaron a Isaac Newton a descubrir la Teoría de la Gravitación Universal, quizás el logro científico más notable de todos los tiempos, casi como una consecuencia lógica de dichas leyes y las suyas propias sobre el movimiento de los cuerpos en general, conocidas hoy como las tres leyes de Newton.
El primer apartado de esta unidad interactiva, con el propósito de motivar el estudio de esta primera Ley de Kepler, presenta extractos de la película Ágora del cineasta Alejandro Amenúbar. En ellos Hipatia se esfuerza en comprender ciertas incongruencias entre las observaciones astronómicas y el modelo heliocéntrico de Aristarco. Como conocía perfectamente las curvas cónicas, la película especula que quizás Hipatia pudo llegar a concebir las trayectorias elípticas, aunque sabemos que quien realmente hizo esto fué Johannes Kepler un milenio más tarde.
Se presenta, además, una escena en la que se muestran las órbitas elípticas de los planetas señalando en ellas con dos colores las áreas barridas en una doceava parte del período de cada planeta.
En particular en el caso de la Tierra estas áreas corresponden aproximadamente a los $12$ meses del año terrestre. Además se discuten las implicaciones sobre la rapidez de los planetas de esta Segunda ley, en particular el hecho de que ésta es mayor en el perihelio y menor en el afelio. Observa la unidad para que descubras otros datos interesantes acerca de esta segunda Ley de Kepler.
La tercera ley de Kepler
La tercera ley de Kepler establece que el cuadrado del período es proporcional al cubo del semieje mayor de la órbita. En el apartado de Órbitas de Satélite y Energía, derivamos la tercera ley de Kepler para el caso especial de una órbita circular. La ecuación 10.8 nos da el período de una órbita circular de radio r sobre la Tierra:
Para una elipse, recuerda que el eje semi mayor es la mitad de la suma del perihelio y el afelio. Para una órbita circular, el semieje mayor (a) es el mismo que el radio de la órbita. De hecho, la Ecuación 10.8 nos da la tercera ley de Kepler si simplemente reemplazamos $r$ por $a$.
Hemos cambiado la masa de la Tierra a $M$, que es más general, ya que esta ecuación se aplica a los satélites que orbitan cualquier masa grande.
Ejemplo 10.13
Órbita del cometa Halley
Determina el eje semi-mayor de la órbita del cometa Halley, dado que llega al perihelio cada $75.3$ años. Si el perihelio es $0.586 \;AU$, ¿qué es el afelio?
Estrategia
Nos dan el período, por lo que podemos reordenar la ecuación 10.11, resolviendo para el eje semi-mayor. Dado que conocemos el valor del perihelio, podemos usar la definición del eje semieje mayor, dado anteriormente en esta sección, para encontrar el afelio.
Notamos que $1$ Unidad Astronómica ($AU$) es el radio promedio de la órbita de la Tierra y se define como $1AU = 1.50 \times 10^{11} m$.
Solución
Reordenando la Ecuación 10.11 e insertando los valores del período del cometa Halley y la masa del Sol, tenemos
$a = \Big(\frac{GM}{4\pi^2}T^2\Big)^{1/3}$
El período en segundos sería: $T = 75.3año \times 365días/año \times 24hr/día \times 3600s/hr = 2.36 \times 10^9 s$
Entonces,
$$a = \Big[\frac{6.67\times 10^{-11} N\cdot m^2/kg^2)(2.00\times 10^{30})}{4\pi^2} (2.36\times 10^9 s)\Big]^{1/3}$$Esto arroja un valor de $2.67 \times 10^{12} m$ o $17.8 AU$ para el eje semi-mayor.
El eje semi mayor es la mitad de la suma del afelio y el perihelio, por lo que tenemos
$$a = \frac12 (\text{afelio + perihelio})$$ $$aphelio = 2a - perihelio$$Sustituyendo los valores, encontramos para el eje semi mayor y el valor dado para el perihelio, encontramos que el valor del afelio es de $35.0 AU$.
Explicación
Edmond Halley, un contemporáneo de Newton, primero sospechó que tres cometas, reportados en 1531, 1607 y 1682, en realidad eran el mismo cometa. Antes de que Tycho Brahe hiciera mediciones de los cometas, se creía que se trataban de eventos únicos, tal vez perturbaciones en la atmósfera y que no se veían afectados por el sol. Halley usó la nueva mecánica de Newton para predecir el regreso de su cometa homónimo en 1758.
 Comprueba tu aprendizaje 10.9
Comprueba tu aprendizaje 10.9
Fuerzas de marea
El origen de las mareas oceánicas de la Tierra ha sido objeto de una investigación continua durante más de 2000 años. Pero se considera que el trabajo de Newton es el comienzo de la verdadera comprensión del fenómeno. Las mareas oceánicas son el resultado de las fuerzas de marea gravitacionales. Estas mismas fuerzas de marea están presentes en cualquier cuerpo astronómico. Son responsables del calor interno que crea la actividad volcánica en Io, una de las lunas de Júpiter, y la desintegración de las estrellas que se acercan demasiado a los agujeros negros.
Mareas lunares
Si vives en la costa del océano casi en cualquier parte del mundo, puedes observar el aumento y la disminución del nivel del mar aproximadamente dos veces al día. Esto es causado por una combinación de la rotación de la Tierra sobre su eje y la atracción gravitatoria de la Luna y el Sol.
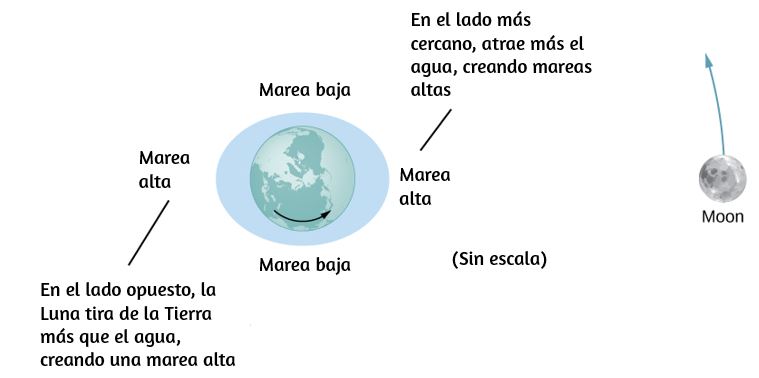
Consideremos primero el efecto de la Luna. En la Figura 10.22, estamos mirando hacia "abajo" hacia el Polo Norte de la Tierra. Un lado de la Tierra está más cerca de la Luna que del otro lado, por una distancia igual al diámetro de la Tierra. Por lo tanto, la fuerza gravitacional es mayor en el lado cercano que en el lado lejano. La magnitud en el centro de la Tierra está entre estos valores. Esta es la razón por la que aparece una protuberancia de marea en ambos lados de la Tierra.
La fuerza neta en la Tierra hace que orbite alrededor del centro de masa de la Tierra-Luna, ubicado a unos $1600 km$ por debajo de la superficie de la Tierra a lo largo de la línea entre la Tierra y la Luna. La fuerza de marea se puede ver como la diferencia entre la fuerza en el centro de la Tierra y la de cualquier otra ubicación.
En la figura 10.23, esta diferencia se muestra a nivel del mar, donde observamos las mareas oceánicas (Ten en cuenta que el cambio en el nivel del mar causado por estas fuerzas de marea se mide desde el nivel del mar de referencia. Vimos antes que la Tierra se hincha muchos kilómetros en el ecuador debido a su rotación. Esto define el nivel del mar de referencia y aquí consideramos solo el bulto de marea más pequeño medido desde ese nivel del mar de referencia).

¿Por qué el aumento y la caída de las mareas ocurren dos veces al día? Mira nuevamente la Figura 10.22. Si la Tierra no estuviera girando y la Luna estuviera fija, entonces las protuberancias permanecerían en la misma ubicación en la Tierra.
En relación con la Luna, las protuberancias permanecen fijas, a lo largo de la línea que conecta la Tierra y la Luna. Pero la Tierra gira (en la dirección mostrada por la flecha azul) aproximadamente cada $24$ horas. En $6$ horas, las ubicaciones cercanas y lejanas de la Tierra se mueven hacia donde se producen las mareas bajas, y 6 horas más tarde, esas ubicaciones vuelven a la posición de pleamar. Dado que la Luna también orbita alrededor de la Tierra aproximadamente cada $28$ días, y en la misma dirección en que gira la Tierra, el tiempo entre las mareas altas (y bajas) es en realidad de aproximadamente $12.5$ horas. El momento real de las mareas se complica por numerosos factores, el más importante de los cuales es otro cuerpo astronómico: el sol.
El efecto del sol en las mareas
Además de las fuerzas de marea de la Luna en los océanos de la Tierra, el Sol también ejerce una fuerza de marea. La atracción gravitatoria del Sol sobre cualquier objeto en la Tierra es casi $200$ veces mayor que la de la Luna. Sin embargo, como mostraremos más adelante en un ejemplo, el efecto de marea del Sol es menor que el de la Luna, pero un efecto significativo sin embargo. Dependiendo de las posiciones de la Luna y el Sol en relación con la Tierra, el efecto de marea neto puede ser amplificado o atenuado.
La figura 10.24 ilustra las posiciones relativas del Sol y la Luna que crean las mareas más grandes, llamadas mareas vivas (o mareas rápidas). Durante las mareas de primavera, la Tierra, la Luna y el Sol están alineados y los efectos de las mareas se suman (Recuerda que las fuerzas de marea causan protuberancias en ambos lados).
La figura 10.24 (c) muestra las posiciones relativas para las mareas más pequeñas, llamadas mareas muertas. Los extremos de las mareas altas y bajas se ven afectados. Las mareas de primavera ocurren durante la luna nueva o llena, y las mareas muertas ocurren en la luna media.
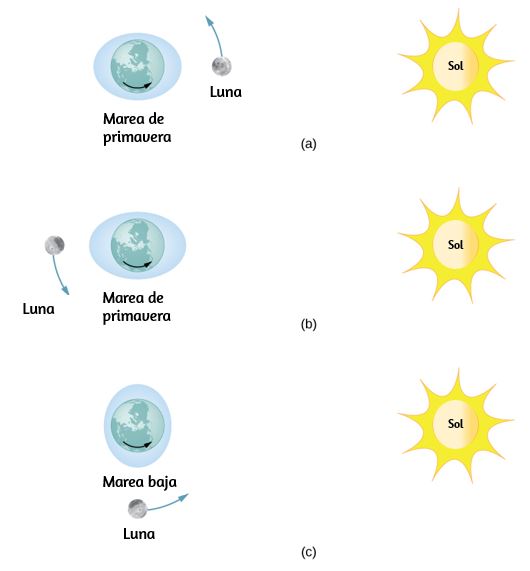
La magnitud de las mareas
Con datos precisos para las posiciones de la Luna y el Sol, el tiempo de las mareas máximas y mínimas en la mayoría de los lugares de nuestro planeta puede predecirse con precisión.
La magnitud de las mareas, sin embargo, es mucho más complicada. Los ángulos relativos de la Tierra y la Luna determinan las mareas de primavera y de verano, pero las magnitudes de estas mareas también se ven afectadas por las distancias de la Tierra.
Las fuerzas de marea son mayores cuando las distancias son más pequeñas. Tanto la órbita de la Luna sobre la Tierra como la de la Tierra alrededor del Sol son elípticas, por lo que una marea de primavera es excepcionalmente grande si ocurre cuando la Luna está en perigeo y la Tierra está en perihelio. Por el contrario, es relativamente pequeño si ocurre cuando la Luna está en apogeo y la Tierra está en afelio.

Las principales causas de la variación de la marea son la topografía de la línea costera local y la batimetría (el perfil de la profundidad) del fondo oceánico. El rango de mareas debido a estos efectos es asombroso. Aunque las mareas oceánicas son mucho más pequeñas que un metro en muchos lugares del mundo, las mareas en la Bahía de Fundy (Figura 10.25), en la costa este de Canadá, pueden llegar a los $16.3$ metros.
Ejemplo 10.14
Comparando las fuerzas de marea
Compara la fuerza gravitacional de la Luna en una masa de $1.0 kg$ ubicada en el lado cercano y otra en el lado opuesto de la Tierra. Repite para el Sol y luego compara los resultados para confirmar que las fuerzas de marea de la Luna son aproximadamente el doble que las del Sol.
Estrategia
Usamos la ley de gravitación de Newton dada por la ecuación 10.1. Necesitamos las masas de la Luna y del Sol y sus distancias desde la Tierra, así como el radio de la Tierra.
Solución
Sustituyendo la masa de la Luna y la distancia media de la Tierra a la Luna (datos consultados en https://es.wikipedia.org/), tenemos
$$\begin{split} F_{12} &= G\frac{m_1}{m_2}{r^2}\\ &= (6.67 \times 10^{−11} N\cdot m^2/kg^2)\frac{(1.0kg)(7.35 \times 10^{22} kg)}{(3.84 \times 10^8 \pm 6.37\times 10^6 m)^2}\\ \end{split}$$En el denominador, usamos el signo menos para el lado cercano y el signo más para el lado lejano. Los resultados son
$$F_{cercano} = 3.44 \times 10^{-5} N\;\; \text{y} \;\;F_{lejano} = 3.22 \times 10^{-5} N$$La fuerza gravitatoria de la Luna es casi un $7\%$ mayor en el lado cercano de la Tierra que en el lado opuesto, pero ambas fuerzas son mucho menores que la de la Tierra en la masa de $1.0 kg$. Sin embargo, esta pequeña diferencia crea las mareas. Ahora repetimos el problema, pero sustituimos la masa del Sol y la distancia media entre la Tierra y el Sol. Los resultados son
$$F_{cercano} = 5.89975 \times 10^{-3} N\;\; \text{y}\;\; F_{lejano} = 5.89874 \times 10^{-3} N$$Tenemos que mantener seis dígitos significativos ya que deseamos comparar la diferencia entre ellos con la diferencia para la Luna (Aunque no podemos justificar el valor absoluto de esta precisión, dado que todos los valores en el cálculo son los mismos excepto las distancias, la precisión en la diferencia sigue siendo válida para tres dígitos). La diferencia entre las fuerzas cercanas y lejanas en un $1.0 kg$ de masa debido a la Luna es
$$F_{cercano} = 3.44 \times 10^{-5} N -3.22 \times 10^{-5} N = 0.22 \times 10^{-5} N$$mientras que la diferencia para el sol es
$$F_{cercano} = 5.89975 \times 10^{-3} N -5.89874 \times 10^{-3} N = 0.101 \times 10^{-5} N$$Ten en cuenta que un enfoque más adecuado es escribir la diferencia en las dos fuerzas con la diferencia entre las distancias cercana y lejana explícitamente expresadas. Con solo un poco de álgebra podemos demostrar que
donde $r_1$ y $r_2$ son iguales a tres dígitos significativos, pero su diferencia ($r_2 - r_1$), igual al diámetro de la Tierra, también se conoce por tres dígitos significativos. Los resultados del cálculo son iguales. Este enfoque sería necesario si el número de dígitos significativos necesarios excede el disponible en tu calculadora o computadora.
Explicación
Ten en cuenta que las fuerzas ejercidas por el Sol son casi $200$ veces mayores que las fuerzas ejercidas por la Luna. Pero la diferencia en esas fuerzas para el Sol es la mitad que para la Luna. Esta es la naturaleza de las fuerzas de marea. La Luna tiene un mayor efecto de marea porque el cambio fraccional en la distancia desde el lado cercano al lado lejano es mucho mayor para la Luna que para el Sol.
 Comprueba tu aprendizaje 10.10
Comprueba tu aprendizaje 10.10
Otros efectos de marea
Las fuerzas de marea existen entre dos cuerpos. El efecto estira los cuerpos a lo largo de la línea entre sus centros.
Aunque el efecto de marea en los mares de la Tierra es observable a diario, las consecuencias a largo plazo no se pueden observar tan fácilmente. Una consecuencia es la disipación de la energía de rotación debido a la fricción durante la flexión de los propios cuerpos. La velocidad de rotación de la Tierra se está desacelerando a medida que las fuerzas de marea transfieren la energía de rotación al calor. El otro efecto, relacionado con esta disipación y conservación del momento angular, se denomina sincronización de bloqueo o de marea. Ya le ha sucedido a la mayoría de las lunas en nuestro sistema solar, incluida la Luna de la Tierra. La Luna mantiene una cara hacia la Tierra: su velocidad de rotación se ha bloqueado en la tasa orbital alrededor de la Tierra. El mismo proceso le está sucediendo a la Tierra, y eventualmente mantendrá una cara hacia la Luna. Si eso sucede, ya no veríamos las mareas, ya que el bulto de las mareas permanecería en el mismo lugar en la Tierra, y la mitad del planeta nunca vería la Luna. Sin embargo, este bloqueo tomará muchos miles de millones de años, tal vez no antes de que expire nuestro Sol.
Uno de los ejemplos más dramáticos de los efectos de las mareas se encuentra en Io, una de las lunas de Júpiter. En 1979, la nave espacial Voyager envió de vuelta imágenes dramáticas de la actividad volcánica en Io. Es el único otro cuerpo astronómico en nuestro sistema solar en el que hemos encontrado tal actividad. La Figura 10.26 muestra una imagen más reciente de Io tomada por la nave espacial New Horizons en su camino a Plutón, mientras utilizaba una asistencia gravitatoria de Júpiter.
Para algunas estrellas, el efecto de las fuerzas de marea puede ser catastrófico. Las fuerzas de marea en sistemas binarios muy cercanos pueden ser lo suficientemente fuertes como para desgarrar la materia de una estrella a la otra, una vez que las fuerzas de marea exceden las fuerzas autogravitacionales cohesivas que mantienen juntas a las estrellas. Este efecto se puede ver en estrellas normales que orbitan cerca de estrellas compactas, como estrellas de neutrones o agujeros negros.

La figura 10.27 muestra la interpretación de este proceso por parte de un artista. A medida que la materia cae en la estrella compacta, forma un disco de acreción que se sobrecalienta y se irradia en el espectro de rayos X.
La producción de energía de estos sistemas binarios puede exceder la producción típica de miles de estrellas. Otro ejemplo podría ser un quasar. Los cuásares son objetos muy distantes e inmensamente brillantes, que a menudo exceden la producción de energía de galaxias enteras.
Es el consenso general entre los astrónomos que son, de hecho, agujeros negros masivos que producen energía radiante cuando la materia que ha sido arrancada de estrellas cercanas cae dentro de ellos.
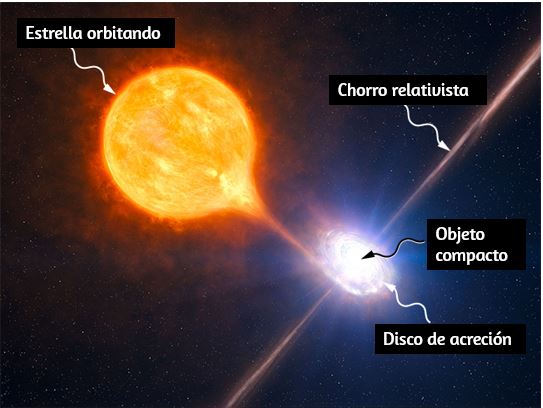
La teoría de la gravedad de Einstein
La ley de Newton de la gravitación universal predice con precisión gran parte de lo que vemos dentro de nuestro sistema solar. De hecho, solo las leyes de Newton han sido necesarias para enviar con precisión cada vehículo espacial en su viaje. Las rutas de los asteroides que cruzan la Tierra y la mayoría de los otros objetos celestes se pueden determinar con precisión únicamente con las leyes de Newton. Sin embargo, muchos fenómenos han mostrado una discrepancia con lo que predicen las leyes de Newton, incluida la órbita de Mercurio y el efecto que la gravedad tiene sobre la luz. En esta sección, examinamos una forma diferente de visualizar la gravitación.
Una revolución en perspectiva
En 1905, Albert Einstein publicó su teoría de la relatividad especial. En esta teoría, ningún movimiento puede exceder la velocidad de la luz; es el límite de velocidad del Universo. Este simple hecho ha sido verificado en innumerables experimentos. Sin embargo, tiene consecuencias increíbles: el espacio y el tiempo ya no son absolutos. Dos personas que se mueven entre sí no concuerdan en la longitud de los objetos o el paso del tiempo. Casi todos los mecanismos que aprendiste en capítulos anteriores, aunque notablemente precisos incluso para velocidades de muchos miles de millas por segundo, comienzan a fallar cuando te acercas a la velocidad de la luz.
Este límite de velocidad en el Universo era también un desafío a la suposición inherente en la ley de gravitación de Newton de que la gravedad es una fuerza de acción a distancia. Es decir, sin contacto físico, cualquier cambio en la posición de una masa se comunica instantáneamente a todas las otras masas. Esta suposición no proviene de ningún primer principio, ya que la teoría de Newton simplemente no aborda la cuestión.
Es justo decir que la mayoría de los científicos no estaban completamente cómodos con el concepto de acción a distancia).
Una segunda suposición también aparece en la ley de gravitación de Newton Ecuación 10.1. Se supone que las masas son exactamente las mismas que las utilizadas en la segunda ley de Newton, $\bold{\vec{F}} = m\bold{\vec{a}}$. Hicimos esa suposición en muchas de nuestras derivaciones en este capítulo. Una vez más, no hay un principio subyacente que esto debe ser, pero los resultados experimentales son consistentes con esta suposición. En la teoría posterior de la relatividad general de Einstein (1916), se abordaron ambos problemas. Su teoría era una teoría de la geometría espacio-temporal y cómo la masa (y la aceleración) se distorsionan e interactúan con ese espacio-tiempo. No era una teoría de las fuerzas gravitatorias. Las matemáticas de la teoría general están más allá del alcance de este texto, pero podemos ver algunos principios subyacentes y sus consecuencias.
El principio de equivalencia
Einstein llegó a su teoría general en parte al preguntarse por qué alguien que estaba cayendo libremente no sentía su peso. De hecho, es común hablar de astronautas que orbitan la Tierra como ingrávidos, a pesar del hecho de que la gravedad de la Tierra todavía es bastante fuerte allí. En la teoría general de Einstein, no hay diferencia entre la caída libre y la ausencia de peso. Esto se llama el principio de equivalencia. El corolario igualmente sorprendente de esto es que no hay diferencia entre un campo gravitatorio uniforme y una aceleración uniforme en ausencia de gravedad. Vamos a centrarnos en esta última declaración. Aunque un campo gravitatorio perfectamente uniforme no es factible, podemos aproximarlo muy bien.
Dentro de un laboratorio de tamaño razonable en la Tierra, el campo gravitacional $\bold{\vec{g}}$ es esencialmente uniforme.
El corolario establece que cualquier experimento físico realizado allí tiene los mismos resultados que los realizados en un laboratorio que se aceleran en $\bold{\vec{a}} = \bold{\vec{g}}$ en el espacio profundo, lejos de todas las demás masas. La figura 10.28 ilustra el concepto.
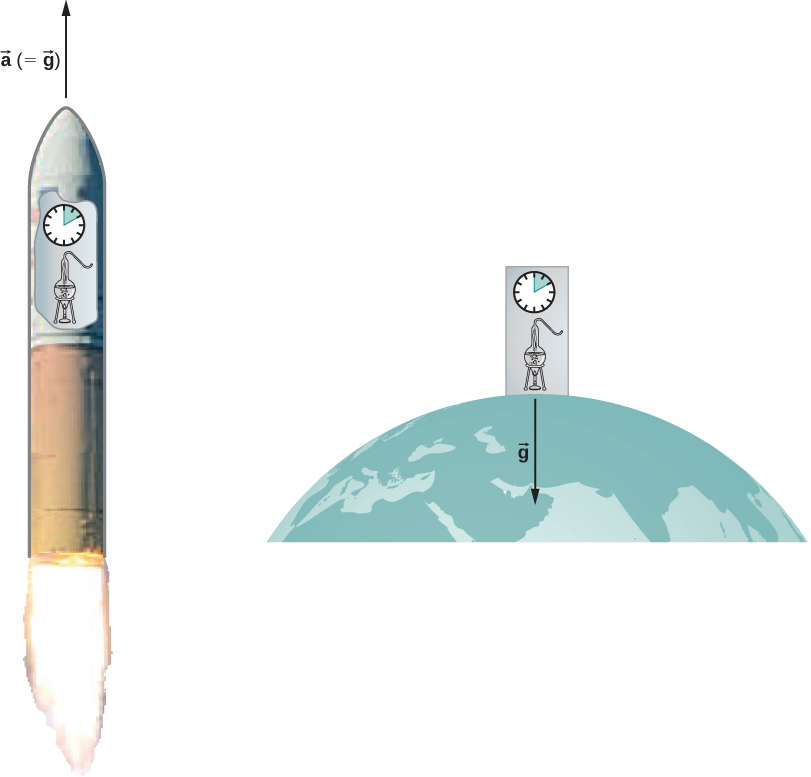
¿Cómo pueden estas dos situaciones aparentemente fundamentalmente diferentes ser las mismas? La respuesta es que la gravitación no es una fuerza entre dos objetos, sino que es el resultado de que cada objeto responde al efecto que el otro tiene en el espacio-tiempo que lo rodea. Un campo gravitatorio uniforme y una aceleración uniforme tienen exactamente el mismo efecto en el espacio-tiempo.
Una teoría geométrica de la gravedad
La geometría euclidiana asume un espacio "plano" en el cual, entre los atributos más comúnmente conocidos, una línea recta es la distancia más corta entre dos puntos, la suma de los ángulos de todos los triángulos debe ser de $180$ grados y las líneas paralelas nunca se cruzan. La geometría no euclidiana no se investigó seriamente hasta el siglo XIX, por lo que no es sorprendente que el espacio euclidiano se asuma intrínsecamente en todas las leyes de Newton.
La teoría general de la relatividad desafía esta suposición largamente sostenida. Solo el espacio vacío es plano. La presencia de masa (o energía, ya que la relatividad no distingue entre las dos) distorsiona o curva el espacio y el tiempo, o espacio-tiempo, a su alrededor. El movimiento de cualquier otra masa es simplemente una respuesta a este espacio-tiempo curvo. La figura 10.29 es una representación bidimensional de una masa más pequeña que orbita en respuesta al espacio distorsionado creado por la presencia de una masa más grande. En una imagen más precisa pero confusa, también veríamos un espacio distorsionado por la masa en órbita, y ambas masas estarían en movimiento en respuesta a la distorsión total del espacio. Ten en cuenta que la figura es una representación para ayudar a visualizar el concepto. Estas son distorsiones en nuestro espacio y tiempo tridimensional. No los vemos como lo haríamos con un hoyuelo en una pelota.
Vemos la distorsión solo mediante mediciones cuidadosas del movimiento de los objetos y la luz a medida que se mueven a través del espacio.

Para los campos gravitacionales débiles, los resultados de la relatividad general no difieren significativamente de la ley de gravitación de Newton. Pero para los campos gravitacionales intensos, los resultados divergen, y la relatividad general ha demostrado predecir los resultados correctos. Incluso en el campo gravitacional relativamente débil de nuestro Sol a la distancia de la órbita de Mercurio, podemos observar el efecto. A partir de mediados de la década de 1800, la órbita elíptica de Mercurio se midió cuidadosamente.
Sin embargo, aunque es elíptico, su movimiento se complica por el hecho de que la posición del perihelio de la elipse avanza lentamente. La mayor parte del avance se debe a la atracción gravitacional de otros planetas, pero una pequeña parte de ese avance no puede explicarse por la ley de Newton. En un momento, incluso hubo una búsqueda de un planeta "acompañante" que explicaría la discrepancia. Pero la relatividad general predice correctamente las mediciones. Desde entonces, muchas mediciones, como la desviación de la luz de objetos distantes por el Sol, han verificado que la relatividad general predice correctamente las observaciones.
Cerramos esta discusión con un comentario final. A menudo nos hemos referido a las distorsiones del espacio-tiempo o a las distorsiones tanto en el espacio como en el tiempo. Tanto en la relatividad especial como en la general, la dimensión del tiempo tiene un pie de igualdad con cada dimensión espacial (que difiere en su lugar en ambas teorías solo por un factor de escala en última instancia sin importancia). Cerca de una masa muy grande, no solo se "estira" el espacio cercano, sino que el tiempo se dilata o se "ralentiza".
Agujeros negros
La teoría de la gravitación de Einstein se expresa en una ecuación tensorial engañosamente simple (los tensores son una generalización de escalares y vectores), que expresa cómo una masa determina la curvatura del espacio-tiempo a su alrededor. Las soluciones a esa ecuación producen una de las predicciones más fascinantes: el agujero negro. La predicción es que si un objeto es suficientemente denso, colapsará sobre sí mismo y estará rodeado por un horizonte de sucesos del que nada puede escapar. El nombre de "agujero negro", que fue acuñado por el astrónomo John Wheeler en 1969, se refiere al hecho de que la luz no puede escapar de tal objeto.
Karl Schwarzschild fue la primera persona en notar este fenómeno en 1916, pero en ese momento, se consideraba principalmente como una curiosidad matemática.
Sorprendentemente, la idea de un cuerpo masivo del que la luz no puede escapar data de fines del siglo XVIII. Independientemente, John Michell y Pierre Simon Laplace usaron la ley de gravitación de Newton para mostrar que la luz que salía de la superficie de una estrella con suficiente masa no podía escapar. Su trabajo se basó en el hecho de que Ole Roemer había medido la velocidad de la luz en 1676. Notó discrepancias en los datos del período orbital de la luna Io sobre Júpiter. Roemer se dio cuenta de que la diferencia surgía de las posiciones relativas de la Tierra y Júpiter en diferentes momentos y que podía encontrar la velocidad de la luz a partir de esa diferencia. Michell y Laplace se dieron cuenta de que, dado que la luz tenía una velocidad finita, podría haber una estrella lo suficientemente grande como para que la velocidad de escape de su superficie pudiera exceder esa velocidad. Por lo tanto, la luz siempre recaería en la estrella. Curiosamente, los observadores lo suficientemente lejos de las estrellas más grandes no podrían verlos, sin embargo, podrían ver una estrella más pequeña desde la misma distancia.
Recordemos que anteriormente, encontramos que la velocidad de escape, dada por la Ecuación 10.6, es independiente de la masa del objeto que escapa. Aunque la naturaleza de la luz no se entendía del todo en ese momento, la masa de luz, si la tenía, no era relevante. Por lo tanto, la ecuación 10.6 debería ser válida para la luz. Sustituyendo $c$, la velocidad de la luz, por la velocidad de escape, tenemos
$$v_{esc} = c = \sqrt{2GM/R}$$Por lo tanto, solo necesitamos valores para $R$ y $M$ tales que la velocidad de escape exceda $c$, y entonces la luz no podrá escapar. Michell postuló que si una estrella tuviera la densidad de nuestro Sol y un radio que se extendiera justo más allá de la órbita de Marte, entonces la luz no podría escapar de su superficie. También conjeturó que todavía podríamos detectar una estrella de este tipo por el efecto gravitacional que tendría sobre los objetos que la rodeaban.
Esta fue una conclusión reveladora, ya que así es como deducimos la existencia de tales objetos en la actualidad. Aunque todavía tenemos que visitar un agujero negro, y tal vez nunca lo hagamos, la evidencia circunstancial para ellos se ha vuelto tan convincente que pocos astrónomos dudan de su existencia.
Antes de examinar parte de esa evidencia, volvamos nuestra atención a la solución de Schwarzschild a la ecuación del tensor de la relatividad general. En esa solución surge un radio crítico, ahora llamado radio de Schwarzschild ($R_S$). Para cualquier masa $M$, si esa masa se comprimiera en la medida en que su radio sea menor que el radio de Schwarzschild, entonces la masa se colapsará a una singularidad, y todo lo que pase dentro de ese radio no podrá escapar. Una vez dentro de $R_S$, la flecha del tiempo lleva todas las cosas a la singularidad (En un sentido matemático amplio, una singularidad es donde el valor de una función va al infinito. En este caso, es un punto en el espacio de volumen cero con una masa finita. Por lo tanto, la densidad de masa y la energía gravitacional se vuelven infinitas). El radio de Schwarzschild está dado por
Si miras nuestra ecuación de velocidad de escape con $v_{esc} = c$, notarás que da precisamente este resultado. Pero eso es simplemente un accidente fortuito causado por varias suposiciones incorrectas. Una de estas suposiciones es el uso de la expresión clásica incorrecta para la energía cinética para la luz. ¿Qué tan denso debe ser un objeto para convertirse en un agujero negro?
Ejemplo 10.15
Cálculo del radio de Schwarzschild
Calcula el radio de Schwarzschild tanto para el Sol como para la Tierra. Compara la densidad del núcleo de un átomo con la densidad requerida para comprimir la masa de la Tierra uniformemente a su radio de Schwarzschild. La densidad de un núcleo es de aproximadamente $2,3 \times 10^{17} kg/m^3$.
Estrategia
Usamos la ecuación 10.12 para este cálculo. Necesitamos solo las masas de la Tierra y el Sol, que obtenemos de https://es.wikipedia.org/).
Solución
Sustituyendo la masa del Sol, tenemos
$$\begin{split} R_S &= \frac{2GM}{c^2}\\ &= \frac{2(6.67 \times 10^{-11} n\cdot m^2/kg^2)81.99 \times 10^{30} kg)}{(3 \times 10^8 m/s)^2}\\ &= 2.95 \times 10^3 m \end{split}$$Este es un diámetro de solo alrededor de $6 km$. Si usamos la masa de la Tierra, obtenemos $R_S = 8.85 \times 10^{-3} m$. ¡Este es un diámetro de menos de $2 cm$! Si empacamos la masa de la Tierra en una esfera con el radio $R_S = 8.85 \times 10^{-3} m$, obtenemos una densidad de
$$\rho = \frac{masa}{volumen} = \frac{5.97 \times 10^{24} kg}{(4/3\pi)(8.85 \times 10^{−3} m)^3} = 2.06 \times 10^{30} kg/m^3$$Explicación
Una estrella de neutrones es el objeto más compacto conocido, fuera de un agujero negro. La estrella de neutrones está compuesta de neutrones, con la densidad de un núcleo atómico y, como muchos agujeros negros, se cree que es el remanente de una supernova, una estrella que explota al final de su vida. Para crear un agujero negro desde la Tierra, tendríamos que comprimirlo a una densidad trece órdenes de magnitud mayor que la de una estrella de neutrones. Este proceso requeriría una fuerza inimaginable. No se conoce ningún mecanismo que pueda causar que un objeto del tamaño de la Tierra se convierta en un agujero negro. Para el Sol, debería ser capaz de mostrar que debería comprimirse a una densidad de solo $80$ veces la de un núcleo (Nota: una vez que la masa se comprime dentro de su radio de Schwarzschild, la relatividad general dicta que se colapsará a una singularidad. Estos cálculos simplemente muestran la densidad que debemos alcanzar para iniciar ese colapso).
 Comprueba tu aprendizaje 10.11
Comprueba tu aprendizaje 10.11
El horizonte de eventos
El radio de Schwarzschild también se denomina horizonte de sucesos o eventos de un agujero negro. Observamos que tanto el espacio como el tiempo se extienden cerca de objetos masivos, como los agujeros negros. La figura 10.30 ilustra ese efecto en el espacio. La distorsión causada por nuestro Sol es en realidad bastante pequeña, y el diagrama está exagerado para mayor claridad. Considera la estrella de neutrones, descrita en el Ejemplo 10.15. Aunque la distorsión del espacio-tiempo en la superficie de una estrella de neutrones es muy alta, el radio es aún mayor que su radio de Schwarzschild. Los objetos aún podrían escapar de su superficie.
Sin embargo, si una estrella de neutrones gana masa adicional, eventualmente se colapsaría, encogiéndose más allá del radio de Schwarzschild. Una vez que eso ocurra, toda la masa se vería arrastrada, inevitablemente, a una singularidad. En el diagrama, el espacio se estira hasta el infinito. El tiempo también se estira hasta el infinito. Cuando los objetos caen hacia el horizonte de sucesos, los vemos acercarse cada vez más lentamente, pero nunca alcanzan el horizonte de sucesos.
En el siguiente vídeo verás un ejemplo animado de estas distorsiones espacialesEl agujero negro deforma el espacio hace parte de la película de ESA "15 años de descubrimiento", la cual se encuentra en la página del 15° aniversario del ESA Hubble. (Crédito: ESA/Hubble (M. Kornmesser y L. L. Christensen)..
La evidencia de los agujeros negros
Hasta la década de 1960, cuando se descubrió la primera estrella de neutrones, no se renovó el interés en la existencia de los agujeros negros. La evidencia de agujeros negros se basa en varios tipos de observaciones, como el análisis de radiación de binarios de rayos X, lentes gravitacionales de la luz de galaxias distantes y el movimiento de objetos visibles alrededor de parejas invisibles. Nos enfocaremos en estas observaciones posteriores según se relacionan con lo que hemos aprendido en este capítulo.
Aunque la luz no puede escapar de un agujero negro para que podamos ver, podemos ver el efecto gravitatorio del agujero negro en las masas circundantes.
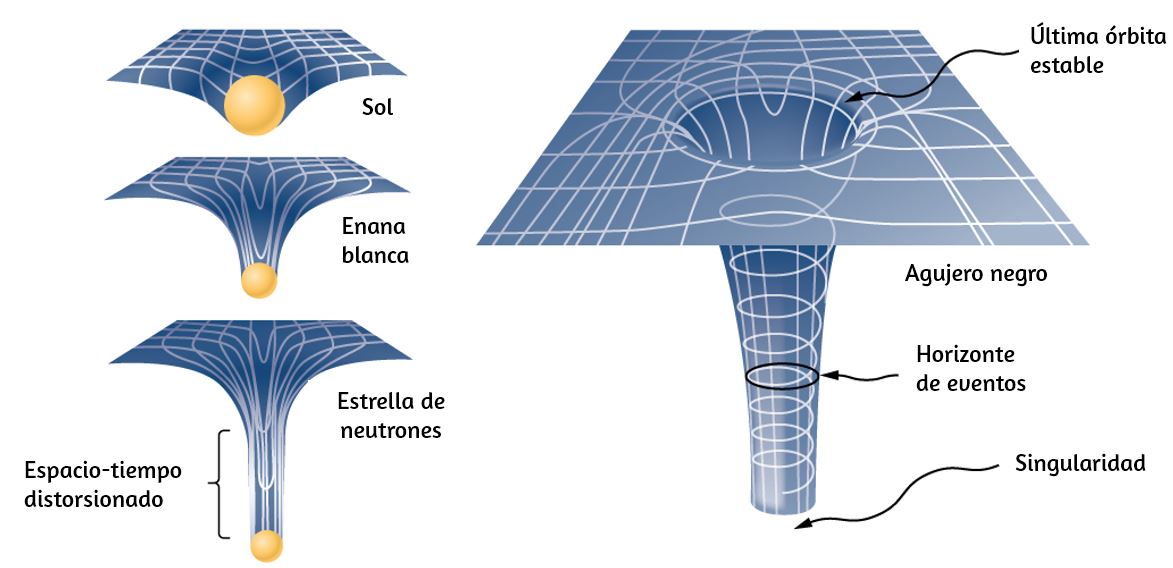
La evidencia más cercana, y tal vez la más dramática, de un agujero negro está en el centro de nuestra Vía Láctea. El Grupo Galáctico de UCLA, utilizando datos obtenidos por los telescopios W. M. Keck, ha determinado las órbitas de varias estrellas cerca del centro de nuestra galaxia. Algunos de esos datos se muestran en la figura 10.31. Las órbitas de dos estrellas están resaltadas. A partir de las mediciones de los períodos y tamaños de sus órbitas, se estima que están en órbita alrededor de una masa de aproximadamente 4 millones de masas solares.
Ten en cuenta que la masa debe residir en la región creada por la intersección de las elipses de las estrellas. La región en la que debe residir esa masa encajaría dentro de la órbita de Mercurio; sin embargo, no se ve nada allí en el espectro visible.
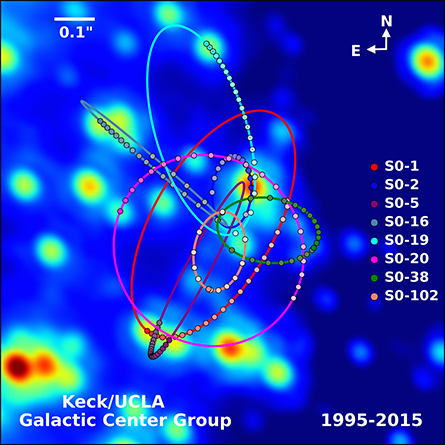
La física de la creación y evolución estelar está bien establecida. La fuente de energía máxima que hace brillar a las estrellas es la energía autogravitacional que desencadena la fusión. El comportamiento general es que cuanto más masiva es una estrella, más brillante brilla y más corta es su vida.
La inferencia lógica es que una masa que es $4$ millones de veces la masa de nuestro Sol, confinada a una región muy pequeña, y que no se puede ver, no tiene otra interpretación viable que no sea un agujero negro. Las observaciones extragalácticas sugieren fuertemente que los agujeros negros son comunes en el centro de las galaxias.
La Materia oscura
Las estrellas que orbitan cerca del corazón de nuestra galaxia proporcionan una fuerte evidencia de un agujero negro allí, pero las órbitas de las estrellas lejos del centro sugieren otro fenómeno intrigante que también se observa indirectamente. Recordemos que podemos considerar que la masa para objetos esféricos se ubicará en un punto en el centro para calcular sus efectos gravitacionales sobre otras masas. De manera similar, podemos tratar la masa total que se encuentra dentro de la órbita de cualquier estrella de nuestra galaxia como si estuviera ubicada en el centro del disco de la Vía Láctea. Podemos estimar esa masa contando las estrellas visibles e incluir en nuestra estimación la masa del agujero negro en el centro también.
Pero cuando hacemos eso, encontramos que la velocidad orbital de las estrellas es demasiado rápida para ser causada por esa cantidad de materia. La figura 10.32 muestra las velocidades orbitales de las estrellas en función de su distancia desde el centro de la Vía Láctea. La línea azul representa las velocidades que esperaríamos de nuestras estimaciones de la masa, mientras que la curva verde es lo que obtenemos de las mediciones directas. Aparentemente, hay una gran cantidad de materia que no vemos, que se estima que es aproximadamente cinco veces más de lo que vemos, por lo que se ha denominado materia oscura. Además, el perfil de velocidad no sigue lo que esperamos de la distribución observada de las estrellas visibles. No solo la estimación de la masa total es inconsistente con los datos, sino que la distribución esperada también es inconsistente.
Y este fenómeno no está restringido a nuestra galaxia, sino que parece ser una característica de todas las galaxias. De hecho, el problema se observó por primera vez en la década de 1930 cuando se midió que las galaxias dentro de los conglomerados estaban en órbita alrededor del centro de masas de esos conglomerados más rápido de lo que deberían basarse en estimaciones de masa visibles.
Hay dos ideas predominantes de lo que podría ser este asunto: WIMPs y MACHOs. WIMPs significa partículas masivas de interacción débil. Estas partículas (los neutrinos son un ejemplo) interactúan muy débilmente con la materia ordinaria y, por lo tanto, son muy difíciles de detectar directamente. MACHOs significa objeto astrofísico masivo de halo compacto, que se componen de materia bariónica ordinaria, como neutrones y protones. Hay problemas sin resolver con estas dos ideas, y se necesitará mucha más investigación para resolver el misterioEn astrofísica se denominan MACHOs (de su acrónimo en inglés: Massive astrophysical compact halo object) u objeto astrofísico masivo de halo compacto a cualquiera de los tipos de cuerpos astronómicos que puedan utilizarse para explicar la presencia de materia oscura en los halos galácticos, es decir, es una forma general de llamar a objetos másivos difíciles de detectar.
Un MACHO es un objeto pequeño de materia bariónica que se mueve por el espacio interestelar de manera aislada (no se encuentra asociado a ningún sistema solar) y que emite muy poca o ninguna radiación. El hecho de no emitir luz propia los hace muy difíciles de detectar. Mientras cumplan estas características, dentro de la categoría de MACHOs pueden entrar diferentes tipos de objetos, desde agujeros negros o estrellas de neutrones a enanas marrones o planetas aislados, incluso se han propuesto como MACHOs enanas blancas y enanas rojas muy débiles. Es un tipo de materia oscura propuesta en la teoría del big bang que ayudaría a explicar el comportamiento gravitatorio de las galaxias, tanto a escala individual como en el interior de cúmulos (https://es.wikipedia.org)..
