Aprendemos a resolver problemas con Descartes y Wiris
Escrito por José Antonio Salgueiro González
Aprendemos a resolver problemas con Descartes es una iniciativa del Departamento de Matemáticas del IES Bajo Guadalquivir de Lebrija, realizada con alumnos y alumnas de 4º ESO durante el curso escolar 2015/2016, basada en la experiencia para el "Desarrollo de la comunicación audiovisual a través de las Matemáticas con Descartes" y llevaba a cabo anteriormente con el alumnado de 1º de Bachillerato de Ciencias e Ingeniería, con objeto de fomentar en nuestros alumnos y alumnas el aprendizaje de las técnicas necesarias del lenguaje cinematográfico y audiovisual, a la vez que proporcionarles una formación básica que les permita, de forma autónoma, generar y producir sus propios contenidos audiovisuales.
Con el lema “Resolvemos problemas con Descartes“, abrimos un foro de suscripción forzosa en el aula virtual de Matemáticas-4º para coordinar la experiencia, dar las indicaciones, organizar los equipos, elegir los problemas, prestar asesoramiento y fomentar el trabajo en colaboración, aunque también se generaba debate en el día a día del aula física.
Decir que, durante todo el curso, los alumnos y alumnas asistieron a clase con sus portátiles de la Escuela TIC 2.0 que les entregaron cuando se encontraban en 5º de Primaria, usando junto a la PDI el libro digital interactivo del Proyecto ED@D y los cuadernos de trabajo Descartes que incorpora cada unidad interactiva, estando en contacto permanente con el profesor desde el aula virtual y desde la red social Twitter.
| 1ª FASE: PROPUESTA DE PROBLEMAS Y DIFUSIÓN EN TWITTER |
Cada equipo tuvo que seleccionar dos problemas de la unidad interactiva "Ecuaciones y sistemas", concretamente uno de primer grado y otro de segundo, que se encuentran en el menú ejercicios y que se denominan "Sistemas de ecuaciones lineales" y "Sistemas de segundo grado", respectivamente, y comunicarlo en el foro del aula virtual para conocimiento del profesor y del resto de equipos. Posteriormente, y una vez acordado con el profesor los dos problemas seleccionados para su resolución en lo que sería su "ópera prima", al menos en Matemáticas, tuvieron que diseñar una imagen alusiva al contenido de los problemas, incorporar sus enunciados y darle difusión por la red social Twitter con el hashtag del curso #MATES4ABAJO.
| 2ª FASE : DOCUMENTACIÓN Y GUIÓN DE LA OBRA |
Comienza la fase de investigación y documentación, así que damos las indicaciones desde el aula virtual, aportamos sugerencias, consejos y recomendamos espacios y recursos. Por ejemplo:
- Guía rápida para grabar en vídeo. ¡Muy bueno!
- Necesitáis un guión de lo que váis a grabar y a decir, pudiendo alternar planos virtuales de lo que se visualiza en el ordenador, tableta o smartphone con planos reales de la ejecución técnica de los ejercicios, que podéis realizar en una pizarra, en un cuaderno o folio, con un software que lo permita, grabando en interior o en exterior y, por supuesto, todo lo que se os ocurra. Aquí es donde entra en juego vuestra creatividad e imaginación.
- Recordad que publicaremos en internet el producto final, así que procurad la mejor calidad de imagen y audio posibles.
- El lenguaje matemático será primordial para las explicaciones y la comunicación audiovisual, por eso me enviaréis el borrador del guión, a través de la tarea del aula virtual, para que yo pueda revisarlo.
- No podéis usar ni imágenes ni música con derechos de autor. Para estos casos, os recomiendo:
- Banco de imágenes y sonidos del INTEF.
- Imágenes con licencia Creative Commons, del mismo banco anterior o de Pixabay.
- Jamendo, descarga de música libre y gratis.
- En cualquier caso, es recomendable dedicar una página de créditos para citar en el vídeo la autoría y el lugar de procedencia de las imágenes y audios usados.
- Debería aparecer, al menos, el logotipo del IES Bajo Guadalquivir, nuestro instituto.
- Cuando tengáis todo preparado y ensayado, os aconsejo hacer algunas pruebas de grabación cortas para comprobar si obtenéis el resultado deseado y las calidades demandadas
Si tenéis alguna idea y no sabéis cómo llevarla a efecto, podéis consultar en este foro o por el servicio de mensajería de la Moodle.
¡Es el momento de la CREATIVIDAD E IMAGINACIÓN!
| 3ª FASE : EVALUACIÓN |
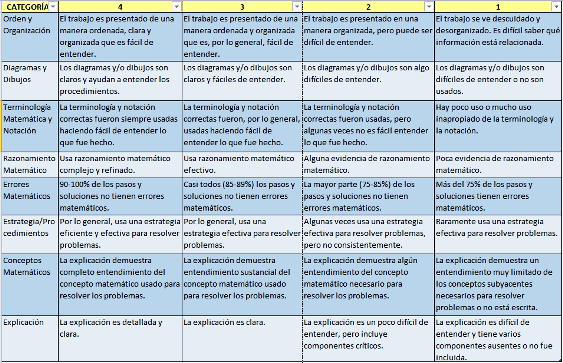
Para la evaluación relativa a los aspectos curriculares del producto final presentado por cada equipo, se ha utilizado la rúbrica que compartimos en este artículo, elaborada desde Rubistar, y que ya empleamos en la experiencia para el "Desarrollo de la comunicación audiovisual a través de las Matemáticas con Descartes". Con un clic sobre la imagen puede ampliarse para una correcta visualización.
Si visualizas y oyes el vídeo con detenimiento, sin duda, encontrarás leves errores de expresión escrita o verbal, tanto en el lenguaje ordinario como en el lenguaje matemático, lo que nos induce a dar una continuidad a la iniciativa y extrapolarla a otros cursos para ir consiguiendo nuestro objetivo paulatinamente. Además, la localización y análisis de errores es una de las mejores estrategias de aprendizaje. No obstante, quiero desde aquí felicitar a todos mis alumnos y alumnas de 4º A por sorprenderme con su creatividad e imaginación, por ser competentes para generar contenido multimedia con sus dispositivos móviles, sin que su profesor sepa ayudarles en este ámbito, por afrontar todos los retos que se han encontrado por el camino hasta conseguir el producto final y por permitirme descubrir y fomentar algunas de sus capacidades ocultas.
Muchas gracias también a sus familias por apoyar la iniciativa autorizando las grabaciones y su difusión por las redes sociales, lo que obviamente repercute en una mejora de la formación de sus hijos e hijas como ciudadanos y ciudadanas del s. XXI y en su preparación para la siguiente etapa educativa.
Construimos una maqueta de las Torres KIO para estudiar las propiedades de la Semejanza
Escrito por José Antonio Salgueiro González
En el proceso de enseñanza y aprendizaje de las Matemáticas, incluso en edades avanzadas, es aconsejable el uso de materiales manipulativos para que el alumnado aprenda haciendo, construyendo y “tocando las matemáticas”. Ahora bien, todos conocemos las dificultades añadidas para organizar y planificar sesiones de aula con grupos numerosos empleando herramientas poco frecuentes, así como el tiempo necesario para diseñar o localizar los recursos que faciliten su desarrollo. Pues bien, este articulo tiene por objeto difundir la experiencia realizada con mi alumnado y, a la vez, compartir los recursos para hacer más llevadera la labor planificadora docente.
Se trata de una actividad ideal para realizar en el aula, para lo que será suficiente con 2 ó 3 sesiones, una vez conocidos los conceptos de figuras semejantes, razón de semejanza y la relación entre sus áreas y volúmenes, obteniendo como producto final una maqueta de las Torres KIO de 9'1 cm de altura, aproximadamente, que podrán manipular, conocer todas sus vistas, hallar el factor de escala y calcular el área de la base y el área lateral de las torres Puerta de Europa y sus volúmenes reales.
Comparto con todos los compañeros, compañeras, amigos y amigas el vídeo de la primera experiencia, desarrollada con un grupo de 2º curso del desaparecido Programa de Cualificación Profesional Inicial, hoy Formación Profesional Básica, con quien tuve la fortuna de trabajar y aprender todo lo que son capaces de conseguir y ofrecer. Una experiencia que he repetido en el curso académico recientemente finalizado con un grupo de alumnos y alumnas de 4º ESO.
Aunque podemos calificar de ingente la cantidad de recursos ofrecidos desde la RED Descartes, posiblemente sea el tratado en este artículo uno de los más desconocidos, por lo que pasaremos a comentar cómo pueden encontrarse y enlazar a los mismos para su descarga o visualización.
- Semejanza, unidad interactiva del Proyecto ED@D para 4º ESO, donde podemos encontrar todo lo necesario para conocer la razón de semejanza en longitudes, áreas y volúmenes, así como los teoremas del cateto y de la altura.
- Ejercicios para practicar la razón de semejanza en longitudes.
- Ejercicios para practicar la razón de semejanza en áreas.
- Ejercicios para practicar la razón de semejanza en volúmenes.
- Actividad 3 de escalas. Volumen de la torre de la maqueta.
- Maqueta de la torre, aplicaciones y solucionario.
Finalmente, después del desarrollo de toda la experiencia, dedicamos un tiempo a visionar y reflexionar sobre la grandiosidad de este proyecto denominado Puerta de Europa y la importancia de la ciencia, tecnología, ingeniería y matemáticas, conocida por las siglas STEM, gracias al vídeo que os recomiendo.
EDAD 3ºESO Ecuaciones de segundo grado
Escrito por Alfonso Saura EspínEsta semana vamos a ver el contenido de 3ºESO de ecuaciones de segundo grado
el índice seguido ha sido el siguiente:
1.Expresiones algebraicas
Identidad y ecuación
Solución de una ecuación
2.Ecuaciones de primer grado
Definición
Método de resolución
Resolución de problemas
3.Ecuaciones de segundo grado
Definición. Tipos
Resolución de ax²+bx=0
Resolución de ax²+c=0
Resolución de ax²+bx+c=0
Suma y producto de las raíces
Discriminante de una ecuación
Ecuación (x-a)·(x-b)=0
Resolución de problemas
Miscelánea: Las Espirales.
Escrito por Ildefonso Fernández TrujilloProporcionalidad. Espirales Aritméticas
Afortunadamente continúan las innovaciones en las posibilidades operativas y de uso de los materiales y Escenas de la Red Descartes. Aconsejamos acudir a los foros y contenidos de la Documentación técnica de la herramienta de autoría DescartesJS para intentar estar al día de las mismas, fundamentalmente a estos, que llevan a la información sobre cómo comunicar las escenas con el HTML y viceversa, y las escenas entre si y a estos otros que ilustran la manera de integrar el cálculo simbólico en las escenas.
También queremos animar a colaborar con los compañeros que están trabajando en el proyecto ed@d en moodle. El material que se está elaborando puede suponer una mejora extraordinaria en la labor educativa con un aumento significativo en la cantidad y calidad de la información expuesta y en la comunicación alumno-alumno, profesor-alumno y viceversa.
En este artículo nos vamos a centrar en la creación de una miscelánea que con el título Las Espirales va a contener una serie de escenas donde se introducirá, estudiará y representará alguna de las siguientes espirales:
- Espiral Aritmética o de Arquímedes
- Espirales arquimedianas. Envolventes Uniformes de: 2, 3, 4, ..., n centros. (Enlace cambiado el 16 de agosto de 2023 al quedar roto el original)
- Espiral de litius
- Espiral de Fermat
- Espiral de Pitágoras (de Teodoro, de caracol...)
- Espilral de Ulam
- Espiral de Cornu
- Espiral de Durero
- Espiral de Fibonacci (Enlace cambiado el 16 de agosto de 2023 al quedar roto el original)
- Espiral Hiperbólica (Enlace cambiado el 16 de agosto de 2023 al quedar roto el original)
- Espiral Logarítmica (Enlace cambiado el 16 de agosto de 2023 al quedar roto el original)
- Espiral de Parker (del viento solar)
- Espiral Cordobesa
Cada elemento de la lista anterior enlaza con una página que puede contener o enlazar a: la definición, la ecuación en polares, las ecuaciones paramétricas, la gráfica y otras características de cada espiral, por lo que la miscelánea que vamos a elaborar estará enfocada a mostrar el proceso de planificación y realización de dicha miscelánea teniendo en cuenta que los objetivos didácticos de cara al alumnado son: las aplicaciones de la proporcionalidad y el potencial de uso de las funciones trigonométricas elementales, logarítmicas y exponenciales.
Aprovecharemos este artículo, los siguientes y la miscelánea que elaboraremos, para la presentación de la espiral Cordobesa, particularización de las espirales gnomónicas y fruto de un largo y laborioso trabajo colaborativo, aún vigente, que nuestro compañero, Ángel Cabezudo Bueno, ha concretado, provisionalmente, con éxito.
No debe olvidarse que estamos estudiando una de las aplicaciones del concepto de Proporcionalidad siguiendo algunos de los materiales que están disponibles en el Proyecto Descartes y, eventualmente, algún otro contenido que por su indudable interés lo merezca.
LAS ESPIRALES ARITMÉTICAS
Al escenario donde va a desarrollarse la acción (E1) le hemos asignado unas dimensiones de 800x612 y dentro de este espacio general definiremos tres espacios rectangulares según muestra la siguiente imagen.
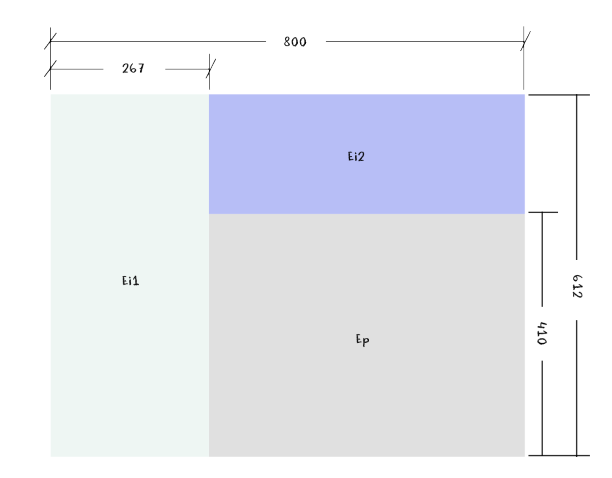
Los espacios Ei1 y Ei2 son, fundamentalmente, informativos aunque, eventualmente, pueden alojar algún elemento interactivo como un botón o un campo de texto. En el espacio Ep es donde se desarrollarán las acciones principales de la primera escena que está dedicada a la espiral Aritmética (de Arquímedes) y al grupo de espirales uniformes de 2, 3,...,n centros.
Comenzaremos trabajando de una forma peculiar, crearemos un solo espacio, el Ep, de dimensiones: 533x410 (conviene observar que 533 y 410 son, aproximadamente, el 67% de 800 y de 612 respectivamente) desarrollaremos todas las acciones de la primera escena que tienen lugar en este espacio con sus interrelaciones y, una vez finalizado este proceso, añadiremos los espacios Ei1 y Ei2, los dotaremos de contenido, y sincronizaremos la acción.
La base teórica de todo el trabajo para esta primera escena va a ser la observación de Arquímedes que originó la espiral que lleva su nombre:"Imaginaos una línea que gira con velocidad constante alrededor de un extremo, manteniéndose siempre en un mismo plano, y un punto que se mueve a lo largo de la línea con velocidad lineal constante: ese punto describirá una espiral"
Creamos el espacio Ep de 533x410 y en él vamos a representar lo descrito en la definición de tres maneras diferentes con objeto de practicar con las funciones seno y coseno y el concepto de proporcionalidad.
- Partiendo de dos segmentos horizontales superpuestos. Uno que gira a derechas y otro que gira a izquierdas.
- Partiendo de dos segmentos horizontales unidos por el punto fijo que giran en el sentido opuesto a las agujas del reloj.
- Partiendo de dos segmentos verticales superpuestos. Uno que gira a derechas y otro que gira a izquierdas.
Consideramos las dos opciones posibles de giro del segmento y algunas de las composiciones que seguramente son conocidas por todos pues son de uso habitual.
También, en esta primera escena, vamos a mostrar la construcción de las espirales uniformes de dos y tres centros lo que unido a las explicaciones informativas que se incluirán en su momento bastará para aprender a construir una espiral uniforme de cualquier número de centros. Esto hace que para mantener el carácter didáctico del código convenga añadir un nuevo espacio, que superpuesto al anterior se hará visible cuando el primero esté oculto.
Para conseguir lo expuesto necesitaremos definir algunos controles de distinto tipo, algún vector, varias funciones, diversos algoritmos de cálculo y bastantes gráficos.
Vamos a mostrar lo que queremos conseguir y luego veremos, paso a paso como lo hemos realizado.
El siguiente vídeo muestra como se ha realizado la escena anterior.
En próximas entradas continuaremos con el paso a paso de la escena, analizando el subproyecto Misceláneas, y las nuevas posibilidades que el código ofrece.
Respecto al trabajo de investigación sobre las espirales gnomónicas en general y sobre la Cordobesa, en particular, que se está desarrollando, queremos mostrar los siguientes avances y animar a aportar alguna ayuda en el proceso de generalización emprendido.
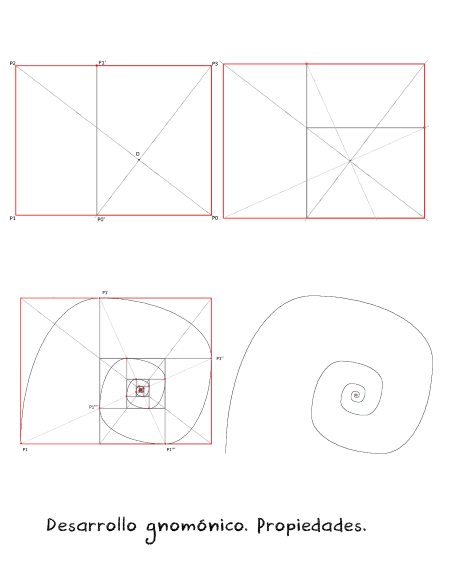
La siguiente escena muestra el avance realizado respecto a las iniciales.Espirales. Proceso de generalización
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo
Más...
Escenas. Misceláneas. Discursos. Unidades.
Escrito por Ildefonso Fernández TrujilloProporcionalidad. Las Espirales
Debido a que, afortunadamente, continúan las innovaciones en las posibilidades operativas y de uso de los materiales y Escenas de la ReDescartes aconsejamos acudir a los contenidos de la Documentación técnica de la herramienta de autoría DescartesJS para intentar estar al día de las mismas, fundamentalmente a estos, que llevan a la información sobre cómo comunicar las escenas con el HTML y viceversa, y las escenas entre sí, a estos otros que ilustran la manera de integrar el cálculo simbólico en las escenas, quedando pendientes los enlaces a algunos de los contenidos de las siguientes novedades:
- Se han publicado nuevos recursos en el subproyecto de Competencias que han sido encargados por el INEE. Son pruebas liberadas del programa PISA para la nueva evaluación de PISA con ordenador.
- Integración de escenas descartes-JS en un paquete Scorm para su uso en Moodle (la profesora Elena Alvarez ha incorporado un ejemplo de integración de Descartes con Moodle mediante un paquete Scorm) y Ficheros de "Juegos Didácticos" para plataformas educativas. de Enric Ripoll Mira
- Experiencia con atención personalizada en matemáticas mediante libro digital en el aula de informática de Juan José López
- ed@d en moodle de Emilio Pazo Núñez.
- Lupa cartesiana de Juan Guillermo Rivera Berrío
este último ya disponible y algunos de los anteriores llevan la documentación incluida o ya están parcialmente disponibles en los foros de la ReDescartes.
En esta ocasión, tal como indica el título, vamos a hacer un recorrido por el concepto de Proporcionalidad siguiendo algunos de los materiales que están disponibles en el Proyecto Descartes y, eventualmente, enlazaremos algún otro contenido por su indudable interés.
El objetivo de incluir el uso y análisis de Unidades Cartesianas sobre la Proporcionalidad es, además del evidente relacionado con el tema, el de aprender a generar una, o varias Misceláneas a partir de dichas unidades o simplemente, a extraer escenas aisladas para un uso ágil y puntual como ejemplo de apoyo a un aspecto concreto de uso o aplicación del concepto en estudio.
El siguiente vídeo muestra la manera de realizar esta acción y de hacer operativo el objeto derivado de la Unidad o Miscelánra.
Antes de continuar conviene observar la manera en que la profesora Antolina Muñoz Huertas enfoca el tema de la Proporcionalidad en la unidad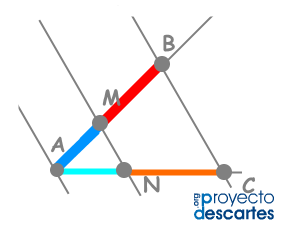 
que publicó en el año 2002 y que he adaptado a DescartesJS debido a la importancia del concepto y a la claridad y sencillez con que se expone. Y también porque de esta Unidad, tal y como más tarde haremos con otros trabajos del profesor José R. Galo Sánchez, vamos a extraer escenas para su posible uso de forma individual.
Una escena tratada aisladamente puede cubrir varios objetivos; unos relacionados con un concepto, por ejemplo la proporcionalidad, otros con una aplicación del concepto p.e. el número de oro y otros con el uso del código que hace comportarse a la escena de la forma que lo hace.
En todos los casos al ser un objeto simple es facil abordar su estudio desde cualquier punto de vista.
El número de oro.
La escena sacada tal cual de la Unidad anterior muestra, de forma dinámica e intuitiva, como dividir un segmento en partes que verifiquen la proporción Divina. Cierto que podemos añadir muchos aspectos que la mejoren hasta convertirla en una excelente Miscelánea, pero en esta ocasión queremos que permanezca tal cual está en origen para así comprender las explicaciones que se dan en el vídeo incluido en este artículo.
A continuación se enlaza una Miscelánea que complementa la Unidad anterior, pues introduce la proporción Humana o Cordobesa y que ha sido creada con objetivos fundamentalmente formativos.
Las dos escenas siguientes están sacadas de la excelente Unidad 
creada por José R. Galo y la tercera es una escena simple que, en su día, se creó para practicar con el Teorema de Pitágoras y con las funciones Trigonométricas: seno, coseno, tangente, arcotangente...
Rectángulo cordobés I
Rectángulo cordobés II
Espiral por puntos.
En esta otra escena, de utilidad si nos planteamos el tema de la proporcionalidad de manera algo más avanzada, tenemos una herramienta que puede ayudar a la confección de espirales logarítmicas, arquimedianas, uniformes de doble centro... y con muy pocas modificaciones de cualquier otro tipo.
Espiral logarítmica
Estando a punto de cerrar este artículo nos llega la noticia de que el profesor Ángel Cabezudo Bueno ha culminado un laborioso trabajo colaborativo y ha dado forma a la Espiral Cordobesa. Aunque dedicaré el próximo artículo a este logro a continuación expongo una escena, aún provisional, con la construción, mediante gnomones, de la espiral.
Espiral cordobesa mediante gnomones
En próximas entradas continuaremos analizando el subproyecto Misceláneas, y las nuevas posibilidades que el código ofrece.
Cálculo simbólico en escenas DescartesJS: Introducción.
La siguiente escena es el ejemplo desarrollado de la implementación del cálculo simbólico dentro de escenas DescartesJS. Realizado por Elena E. Álvarez Sáiz, es un completo estudio que la autora ha realizado de la situación, ampliando los comandos utilizados a más de 400 y detallando la manera de proceder en una amplísima documentación parte de la cual se enlaza al principio del artículo.
De este impresionante avance se ha dicho, entre otras cosas, lo siguiente:
¡Felicitaciones Elena!
Antes de despedir este artículo quisiera hacer mención al impresionante trabajo que hace ya algún tiempo presentaron Deyanira Monroy y José Luis Abreu con el nombre de ConGeo para darlo a conocer a aquellos que aún no lo usan y enviarle a sus autores la petición de incluir en descartes-min.js algunos de los comandos como: Punto Medio, Mediatriz, Bisectriz,... cosa que algún creador de escenas agradecería.
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo
Dentro del curso "Aplicación de juegos didácticos en el aula" que se desarrolló en la 2ª convocatoria de formación de profesorado a nivel regional de la CEJA propusimos a los participantes que compartiesen sus impresiones como forma de mostrar las posibilidades que se abren con el uso de los juegos.
Mª Josefa Chaves Ruiz profesora de 1º de primaria en el CEIP Los Ángeles de Málaga se ha prestado a que publiquemos la experiencia de utilizar los juegos por primera vez con sus alumnos.
El que sean pequeños varía la forma de enfocar la actividad dando más peso al trabajo del docente en el desarrollo de la actividad pero compensa con creces.
Vamos con lo importante, lo que más les gustó a los alumnos:
Ver su nombre en el juego
La puntuación
En el juego de duelo de bombas, cómo estallan las bombas cuando fallan
Actuar de público
Vemos que aunque sean cosas muy simples resultan muy motivadoras
La valoración de Mª Josefa también ha sido muy positiva:
Los objetivos planteados se han conseguido de forma adecuada. El aprendizaje de los contenidos y las competencias básicas ha sido satisfactoria,
La participación ha sido la adecuada, si bien todos querían participar. La convivencia ha sido buena, han respetado el turno del equipo que actuaba, mientras los que no actuaban hacían de público.
También puede parecer un problema trabajar con toda una clase sin tener una sala de ordenadores a tu disposición, siempre podemos encontrar la forma de desarrollar la tarea:
La actividad se ha llevado a cabo durante una hora con 18 alumnos divididos en dos grupos, se han hecho dos equipos de 4 o 5 alumnos que competían entre sí y el resto hacía de público respetando a los que jugaban, después los que hicieron de público fueron los concursantes.
También se han utilizado los juegos con otro pequeño grupo utilizando un portátil, menos medios pero más participación por parte de los alumnos.
Los resultados han sido muy positivos, se han quedado con ganas de volver a jugar, lo que les sirve de incentivo y motivación.
Además, un consejo:
La puesta en práctica hay que prepararla con tiempo para que cuando los alumnos vayan a jugar esté todo preparado y no falle nada.
No podemos terminar de mejor forma que con un último comentario de Mª Josefa:
"A mis alumnos desde luego les ha gustado bastante y siempre que vamos a la pizarra digital quieren jugar con estos juegos, por lo que me veo en la obligación de preparar más preguntas para juegos diferentes. Los encuentro muy motivadores, todos quieren participar."
Solo nos queda agradecer a Mª Josefa su participación en el curso y su colaboración en la difusión de los juegos.
Os animamos a seguir compartiendo vuestras experiencias.
Acceso
Lo último
- Maestría en enseñanza en escenarios digitales con un libro interactivo de la RED Descartes
- Pequeños grandes pensadores: problemas de lógica del Proyecto Canals
- Décimo número de la "Revista Digital RED Descartes"
- Los juegos AJDA como juegos adaptativos
- Octogésimo aniversario de José Luis Abreu ¡FELICIDADES!
Lo más leído de lo publicado hace un mes
- Los juegos AJDA como juegos adaptativos Visto 163 veces
- Décimo número de la "Revista Digital RED Descartes" Visto 126 veces
- Pequeños grandes pensadores: problemas de lógica del Proyecto Canals Visto 84 veces
- Maestría en enseñanza en escenarios digitales con un libro interactivo de la RED Descartes Visto 16 veces
CONTACTO
Canal Youtube
Calculadora Descartes
Versión 3.1 con estadística bidimensional
Código para embeber
Últimos Comentarios
-
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
