En el artículo previo: "Análisis y crítica de la espiral de Durero" les mostré el hilo conductor existente entre la espiral que grabó Durero en su libro "De la Medida", y que registró con el número 27, y la que actualmente se presenta como espiral de Durero cuya particularidad radica en que aproxima a la espiral logarítmica áurea, y quizás de ahí el interés e incentivo que tiene para los seguidores o perseguidores de esta admirada razón de proporcionalidad.

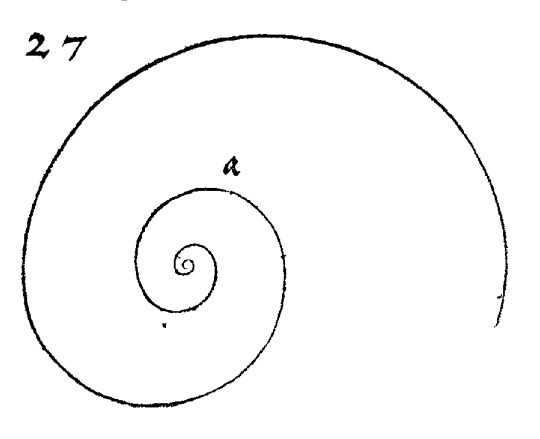
 Fig. 1. ¿Cuál es el hilo conductor entre estas dos espirales?

En ese trabajo, les indiqué que la imprecisión de la instrucciones dadas por Durero para el dibujo de su espiral requería una interpretación de las mismas y que ello conducía a un procedimiento dependiente de dos parámetros: la "amplitud del arco" y el "factor de crecimiento" del radio; y además también observamos que había ambigüedad al no coincidir la contrucción "hacia dentro" con la construcción "hacia fuera". 

En este nuevo artículo lo que haré es considerar esos dos parámetros, reproducir la construcción atendiendo a sus valores y analizar matemáticamente lo obtenido. Observaremos que para cada pareja de valores de los parámetros obtenemos una pseudoespiral de Durero y que cada una de éstas está ligada a una espiral logarítmica que pasa por todos los puntos extremos de los arcos de la construcción y a una segunda espiral, con igual base, que pasa por todos los centros de esos arcos. Ambas espirales coinciden para una infinidad de esas parejas, es decir, para cada amplitud de arco hay un factor de crecimiento en el que coinciden dichas espirales de puntos extremos y centros y viceversa.

Como medio conductor disponemos de una escena interactiva que nos permite indagar y visualizar los hechos demostrados.

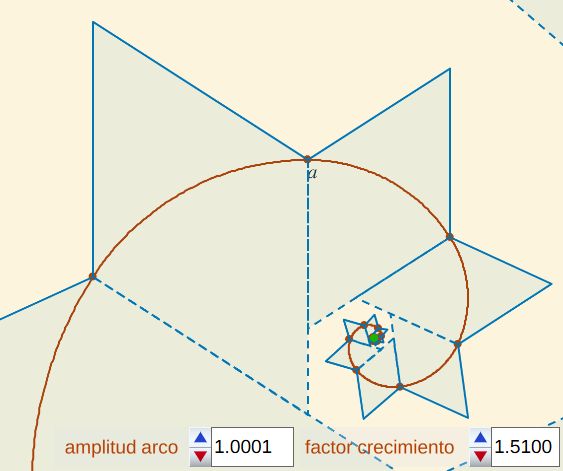
Fig. 2. Escena interactiva "Interpretando a Durero en su pseudoespiral".
Pulse sobre la imagen para acceder.

y con las herramientas auxiliares que se incluyen en ella se pueden aventurar posibles hipótesis y ver bonitas expresiones plásticas que se generan "al jugar" con dichos parámetros y herramientas (ver Fig. 3 y Fig. 4) y que son el reflejo visible de las propiedades matemáticas intrínsecas a su construcción. Pero estos son otros hitos que podemos alcanzar y detallar en otros derroteros.

Fig. 3. "Aliasing" en la pseudoespiral de Durero		Fig. 4. Aproximación al báculo episcopal de Durero

Construcción de la pseudoespiral de Durero fijada una amplitud del arco y un factor de crecimiento del radio 

La construcción de la pseudoespiral, o concatenación de arcos de circunferencia, la realizaremos siguiendo las instrucciones de Durero, pero fijando un valor α para la amplitud del arco y otro m para el factor de crecimiento del radio, los mismos para ambos sentidos de la construcción (hacia dentro y hacia fuera). Así pues, emulando a Durero, procederemos de la siguiente forma:

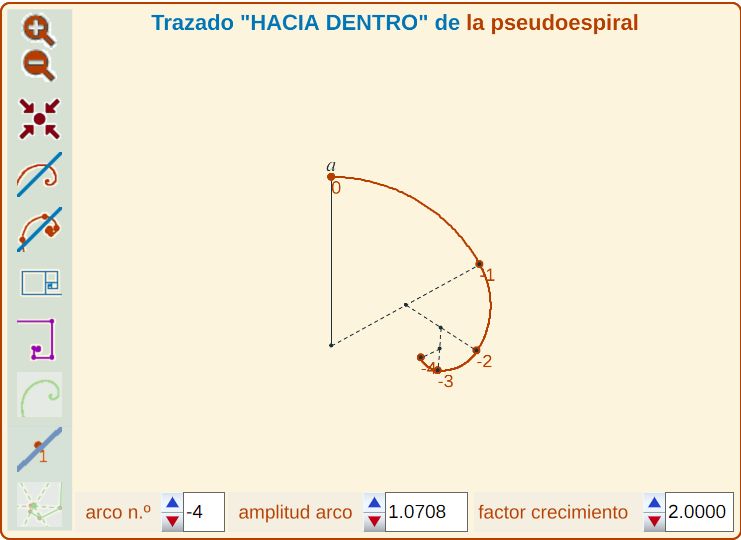
Comienzo con un punto a y trazo esta línea con arcos de círculo hacia dentro con una amplitud "α", como si transcurriera hacia un centro, y cuanto más gira en este sentido el radio es el "1/m  %" del anterior, es decir, el radio anterior es "$m$" veces mayor que el actual (ver Fig. 5 y paso 1 de la escena).

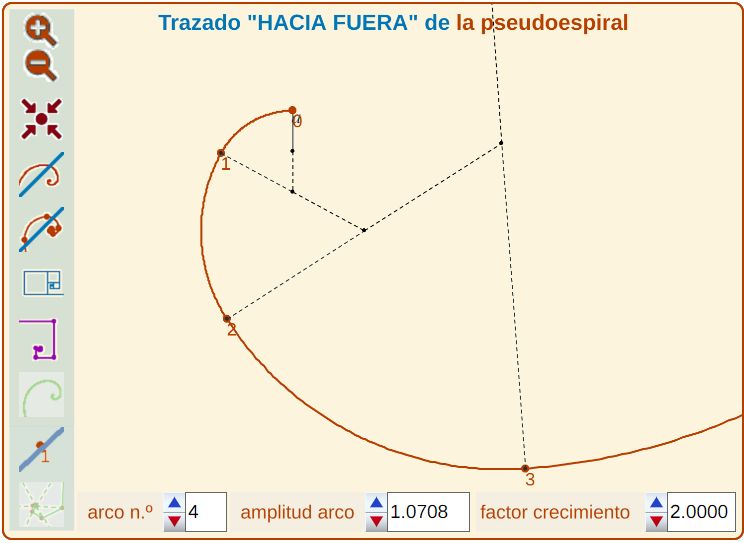
Lo mismo hago al llevar la línea desde a hacia fuera. Trazo arcos de círculo hacia fuera con una amplitud "α", y cuanto más gira en ese sentido, el radio es "$m$" veces mayor que el anterior  (ver Fig. 6 y paso 2 de la escena).

Fig. 5. Construcción hacia dentro (paso 1 de la escena)		Fig. 6. Construcción hacia fuera (paso 2 de la escena)

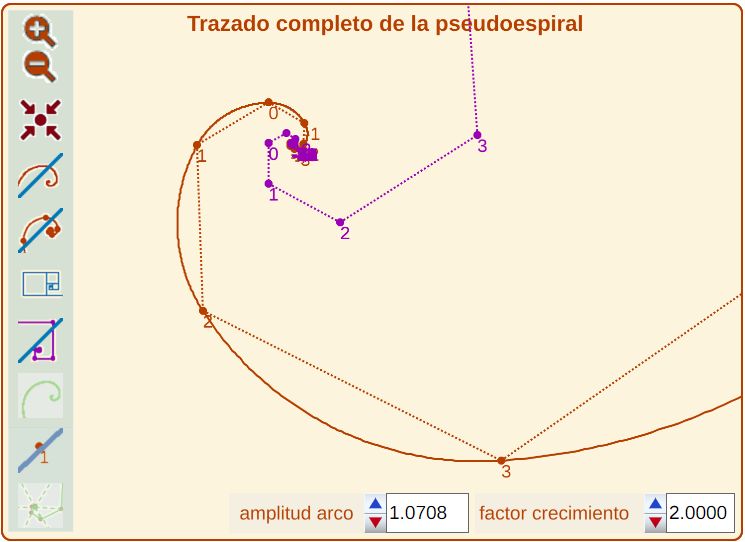
Así que esta línea, cuanto más larga es hacia dentro, más se comprime y cuanto más larga hacia fuera, más se dilata, y nunca tiene fin, ni hacia dentro ni hacia fuera (ver Fig. 7 y paso 3 de la escena).

	Fig. 7. Concatenación de la construcción hacia dentro y hacia fuera (pseudoespiral de Durero). Puntos extremos de los arcos, centros de los mismos y poligonales respectivas que determinan.

Expresión matemática de la pseudoespiral de Durero

En base a las instrucciones indicadas podemos escribir la expresión matemática de dicha pseudoespiral y determinar las coordenadas de los centros y, en particular, las de los puntos extremos de esos arcos de circunferencia.

La pseudoespiral de Durero aproxima a una espiral logarítmica

Es bien conocido que las espirales logarítmicas se denominan también espirales geométricas porque sus radios vectores crecen en progresión geométrica. Así pues, es de esperar que el hecho de que la pseudoespiral se construya como una combinación de un giro de amplitud constante y una amplificación por un factor constante conduzca a que los puntos extremos de los arcos sean puntos de una espiral logarítmica, y así acontece. Para demostrar este resultado nos basaremos en el siguiente Lema, inspirado en las poligonales reflejadas en la Fig. 7:

En consecuencia los puntos extremos de los arcos de la pseudoespiral de Durero son puntos de una espiral logarítmica según observamos en la Fig. 8 y demostramos a continuación:

	Fig. 8. La pseudoespiral de Durero ("hacia dentro" y "hacia fuera"), y espiral logarítmica a la que aproxima

Efecto de la amplitud de arco y el factor de crecimiento del radio en la pseudoespiral de Durero y en la espiral logarítmica asociada

Los centros en la construcción de la pseudoespiral de Durero son puntos de una espiral logarítmica 

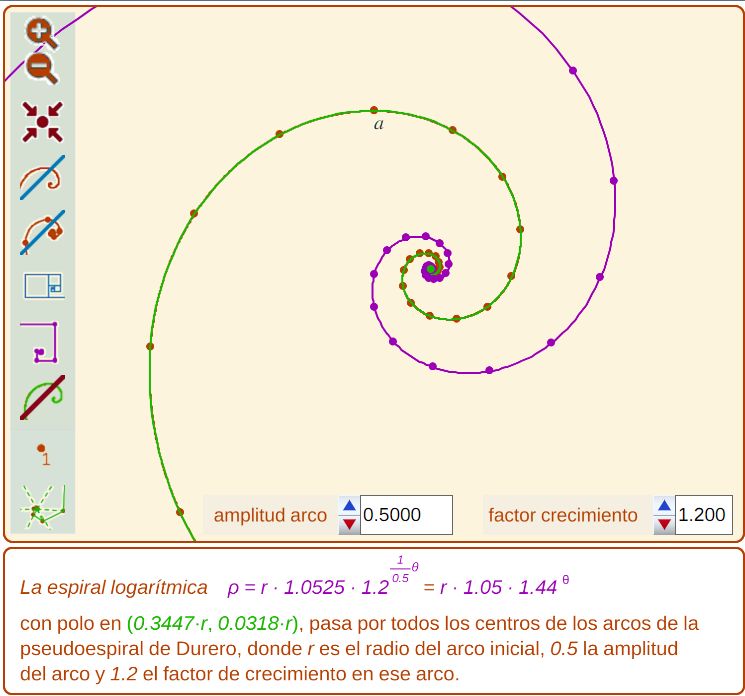
En la construcción de la pseudoespiral de Durero los centros también se obtienen como una combinación de un giro de amplitud constante y una amplificación por un factor constante, por tanto, de manera análoga a lo indicado para los puntos extremos de los arcos, es de esperar que esos centros sean puntos de una espiral logarítmica, y así lo son.

	Fig. 9. Los centros de la construcción de la pseudoespiral de Durero ("hacia dentro" y "hacia fuera"), y espiral logarítmica aproximadora

Relación entre las espirales logarítmicas asociadas a los extremos de los arcos y a los centros de la pseudoespiral de Durero

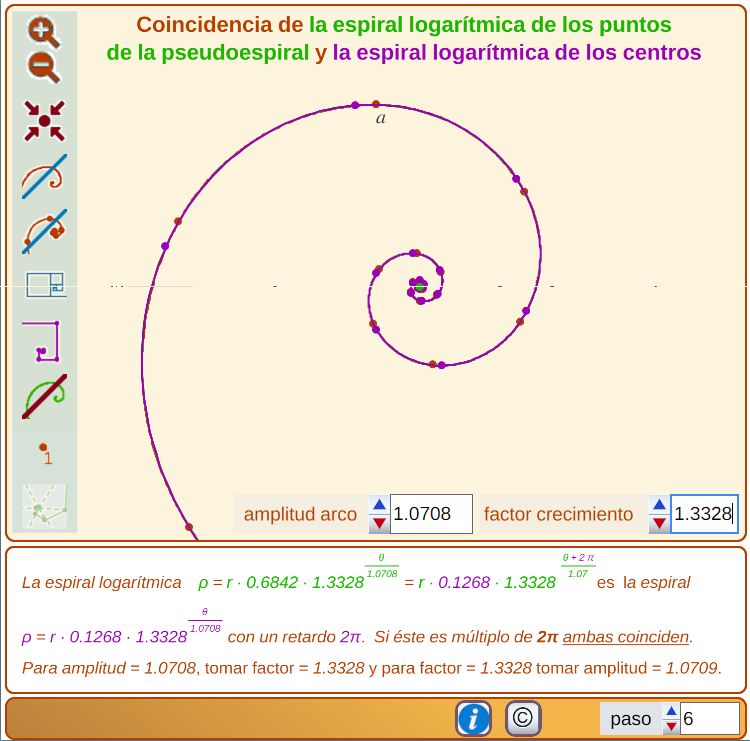
La espiral logarítmica de los puntos extremos de los arcos y la de los centros tienen la misma base, son la misma, per con un ángulo de retardo que equivale a un giro. En particular ambas son idénticas cuando este ángulo sea un múltiplo entero de 2π. Para cada valor de la amplitud "α",se pueden determinar un valor del factor de crecimiento del radio "$m$" (realmente infinitos) para el que ambas espirales coinciden, y viceversa para cada valor del factor del crecimiento del radio. 

	Fig. 10. Coincidencia de la espiral logarítmica asociada a los puntos de la pseudoespiral de Durero y la espiral logarítmica asociada a los centros

En la Fig. 10  podemos ver cómo para m=1,0708 y α=1,3328 ambas espirales coinciden, el ángulo de retardo en este caso es 2π. 

Con este método, en la parte informativa inferior de la escena se muestra para la amplitud de arco α, que elige el usuario en el control correspondiente, cuál es el valor que hay que tomar para el factor de crecimiento para que ambas espirales coincidan con un retardo de 2π y viceversa, elegido el factor m cual es el valor correspondiente para α (ver la última línea en la Fig. 11). Trasladando los valores respectivos elegidos podrá observar esa coincidencia.  

	Fig. 11. Información aportada por la escena para la amplitud y el factor para que la espiral logarítmica asociada a los puntos de la pseudoespiral de Durero y la espiral logarítmica asociada a los centros coincidan

Interpretación realizada

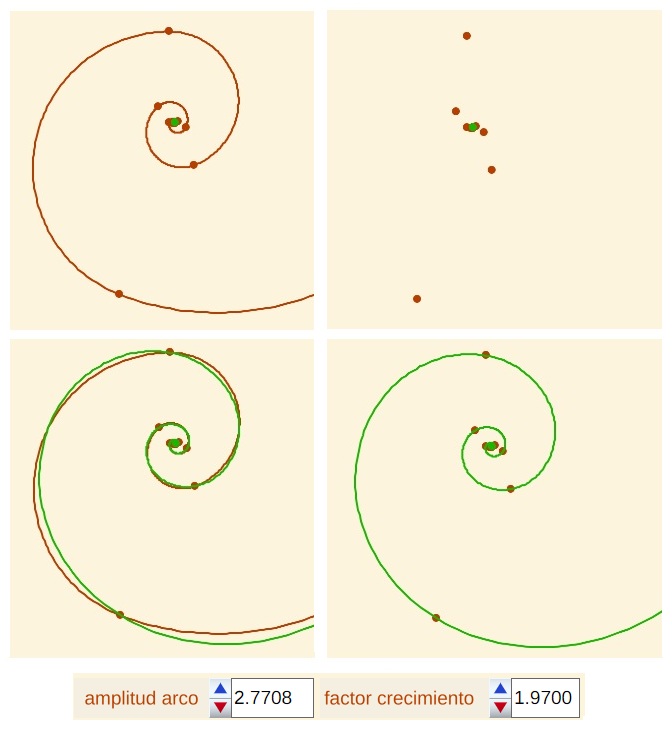
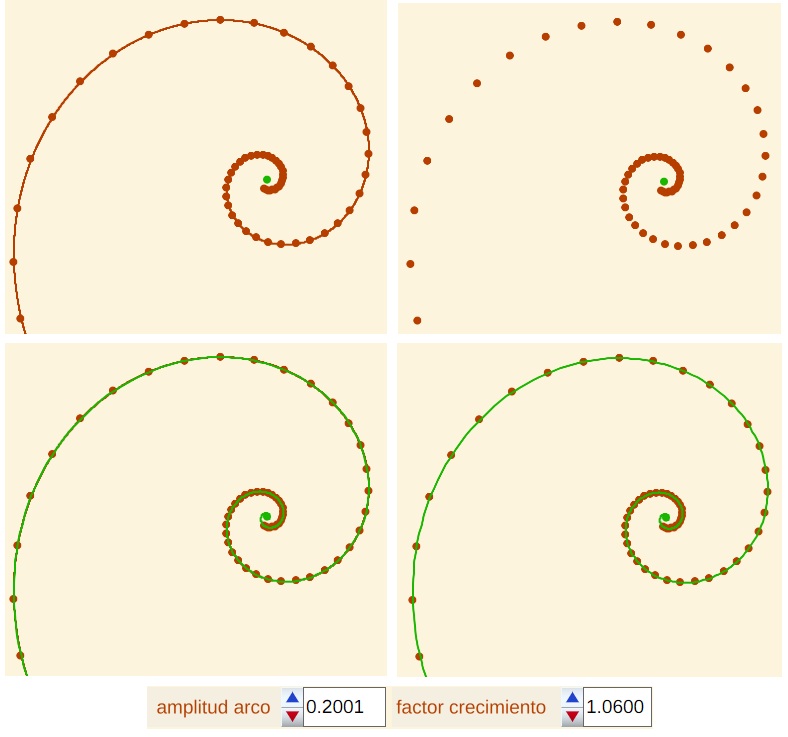
Durero dedicó sólo la mitad de una página a describir, en un único párrafo, cómo obtener una curva que " cuanto más larga es hacia dentro, más se comprime y cuanto más larga hacia fuera, más se dilata, y nunca tiene fin" y a mostrarla gráficamente. Esta consición produce ciertas dudas cuando se quieren seguir las instrucciones que nos legó, pero en esencia, Durero muestra la visión de una curva que tiene coincidencias con la ideada o descrita por Descartes cuando éste abordó la generalización de la circunferencia al buscar una curva equiangular,es decir, aquella que en todo punto el radio vector y la recta tangente forme el mismo ángulo; y también tiene similitudes con la curva que analizó Jakob Bernoulli caracterizada por un crecimiento radial en progresión geométrica y que en su admiración denominó "spira mirabilis", espiral maravillosa. Las curvas descritas por Descartes y Bernoulli son la misma, la que actualmente es más conocida como espiral logarítmica y que se caracteriza por cambiar de manera uniforme en todo punto manteniendo su esencia: "Eadem mutata resurgo", aunque cambiada resurjo igual. Pero la de curva de Durero adolece de esta propiedad ya que al obtenerse mediante concatenaciones de arcos de circunferencia sus cambios se producen en intervalos angulares y consecuentemente no es posible que pueda identificarse con la espiral logarítmica, por ello el que la citemos como pseudoespiral. No obstante, al combinar de manera discreta giros y amplificaciones del radio, si nos fijamos sólo en los puntos extremos de los arcos, estos sí son puntos de una espiral logarítmica (ver Fig. 12 y Fig. 13 para diferentes valores de la amplitud y el factor de crecimiento).

	Fig. 12. Conexión entre la pseudoespiral de Durero (arriba izqda.), los puntos extremos de sus arcos (arriba dcha.) y una espiral logarítmica (abajo dcha.).Superposición de ambas (abajo izqda.).

	Fig. 13. Conexión entre la pseudoespiral de Durero (arriba izqda.), los puntos extremos de sus arcos (arriba dcha.) y una espiral logarítmica (abajo dcha.).Superposición de ambas (abajo izqda.).

En esencia esta es la interpretación que hemos realizado de las instrucciones de Durero, demostrando que si se fija una amplitud de arco y un factor de crecimiento del radio, para cada pareja de valores, los puntos extremos de los arcos son puntos de una espiral logarítmica y los centros de esos arcos son también puntos de la misma espiral logarítmica, pero con un ángulo de retardo.

Toda pseudoespiral de Durero está asociada a una espiral logarítmica 

BIBLIOGRAFÍA

Dürer, Albrecht, and Christian Wechel (1532) Albertus Durerus Nurembergensis pictor huius [a]etatis celeberrimus, versus è Germanica lingua in Latinam, ... adeò exacte quatuor his suarum Institutionum geometricarum libris, lineas, superficies & solida corpora tractauit .... Lutetiae : apud Christianum Wechelum. Consulta en línea (fuente: Biblioteca digital hispánica, Biblioteca nacional de España.

Durero, A. (2000) De la medida.Bogotá: Universidad Jorge Tadeo Lozano. Edición de Jeanne Peiffer y traducción de Jesús Espino. Consulta en línea.

Cardona Suárez, C.A. (2006) La Geometría de Alberto Durero. Madrid, Ediciones Akal, S. A. Consulta en línea.

Galo Sánchez, J.R. (2024) ¡No!, ¡no soy áureo! ¡Soy cordobés! Firmado: Nautilus. Córdoba, Editorial Red Educativa Digital Descartes. ISBN: 978-84-18834-89-9. Consulta en línea.

Galo Sánchez, J.R. (2025) Análisis y crítica de la pseudoespiral de Durero. Revista Digital Red Descartes, Año. 5 - 2025, núm. 10, pp. 40-49. Consulta en línea.