El proyecto @prende.mx es una iniciativa de la Secretaría de Educación Pública de México. Está formado por materiales interactivos para primaria, diseñados para su uso en tabletas usando la herramienta DescartesJS. En su desarrollo han participado el Instituto de Matemáticas de la Universidad Autónoma de México y el Laboratorio de Tecnologías de la Educación (LITE)
En el siguiente vídeo analizamos la unidad Unidades de masa, con actividades para introducir la masa y sus medidas en primaria.
Todas las unidades pertenecientes al proyecto @prende.mx constan de cuatro fases: observa, explora, aprende y prueba. En el apartado observa de la unidad Unidades de masa se pueden ver diferentes imágenes. Situando el ratón sobre cada una de ellas aparece un mensaje indicando la masa del objeto que representa y la unidad en que se mide.
En el apartado explora el alumnado debe completar una tabla de equivalencias entre unidades de masa. Para ello se dispone de una balanza que se debe equilibrar.
En los apartados aprende y prueba, se proponen varios ejercicios de conversiones entre diferentes unidades de masa. Una vez completado el ejercicio, el alumno puede verificar si la respuesta es correcta o no.
Se trata de actividades interactivas autocorrectivas que se pueden realizar tantas veces como se precise ya que se van generando aleatoriamente.
Libros interactivos con Descartes embebido en "Moleskine notebook"
Escrito por Juan Guillermo Rivera BerríoEn este artículo se describe cómo se pueden elaborar libros interactivos donde la interactividad la aporta Descartes y el soporte visual y de navegación viene dado por "Moleskine notebook".
A continuación tienes un ejemplo de libro interactivo diseñado con estas herramientas. Puedes navegar en él.
(Puedes descargar este libro desde este enlace y para verlo en otra pestaña pulsa aquí)
Este nuevo recurso de la Red Educativa Digital Descartes lo hemos definido con el término LIBRO, fundamentado en las siguientes razones:
- Diseño. Su presentación gráfica simula la cubierta y hojas de un libro.
- Animación. La transición entre las páginas es una animación que simula el desplazamiento de natural de una página a otra.
- Interactividad. Según la UNESCO, un libro debe tener 50 o más páginas. Esta afirmación la consideramos válida para libros estáticos; sin embargo, en los libros digitales interactivos, una página no es “una simple página”, en tanto que factores como la interactividad y la aleatoriedad, la convierten en un número indefinido de páginas. La siguiente imagen, que hace parte del libro ejemplo de este tutorial, valida la afirmación anterior.
Si aceptamos los argumentos anteriores, diseñar un libro digital interactivo será algo sencillo para cualquier desarrollador de escenas Descartes. Veamos, entonces, cuál es el procedimiento para ello.
RECURSOS A UTILIZAR
Este tutorial viene acompañado de un libro ejemplo, sobre el cual haremos todas las explicaciones. Los recursos necesarios para diseñar nuestro libro son los siguientes:
- Moleskine Notebook. Hemos realizado una adaptación de este recurso, ampliando el tamaño de las páginas, ajustando fuentes y tamaño de imágenes. El recurso original, se puede descargar desde este enlace: http://tympanus.net/codrops/2010/12/14/moleskine-notebook/.
- Escenas Descartes. Es importante, de acuerdo al tercer argumento planteado para validar nuestro concepto de “Libro”, que las escenas que incluyamos en nuestro libro tengan algo de aleatoriedad. En caso contrario, se podría optar por diseñar 50 páginas, o definirlo simplemente como un folleto.
- Editor de textos. Podría bastar con un editor simple (bloc de notas de Windows, por ejemplo); sin embargo, es recomendable utilizar un editor como Notepad (https://notepad-plus-plus.org/), que presenta las líneas de código en una forma más comprensible para su edición.
Los tres recursos son de acceso y uso libre, lo que facilita el diseño de nuestro libro.
CONTENIDO DEL LIBRO
El modelo que acompaña este tutorial, contiene los siguientes elementos:
- Seis archivos tipo html. Sólo son útiles los archivos index.html e indexb.html, los otros cuatro se han dejado para que el usuario, si lo desea, los consulte o modifique desde el editor de Descartes, pues son las escenas que se incorporarán en el libro. Se pueden eliminar.
- Carpeta audio. Hace parte de la última escena del libro. Para otros diseños no es necesaria, se puede eliminar.
- Carpeta "imagenes". Incluye las imágenes usadas en las escenas Descartes.
- Carpeta "images". Incluye las imágenes usadas por Moleskine.
- Carpeta css. Contiene el archivo style.css, que intervendremos en el diseño.
- Otras carpetas. Todas necesarias, no las intervendremos.
ESCRITORIO
Iniciamos el diseño de nuestro libro con la elección del escritorio. Para darle más realismo a la presentación, Moleskine usa una imagen de fondo que muestra una superficie (escritorio) sobre el que está apoyado el libro. Además de la imagen original, hemos incluido otras que puedes elegir o, si lo prefieres, incluir otra que desees (ver carpeta images).
 Para cambiar el escritorio, abrimos con el editor de textos el archivo style.css, que se encuentra en la carpeta css. Luego cambiamos el nombre de la imagen en la línea seis:
Para cambiar el escritorio, abrimos con el editor de textos el archivo style.css, que se encuentra en la carpeta css. Luego cambiamos el nombre de la imagen en la línea seis: 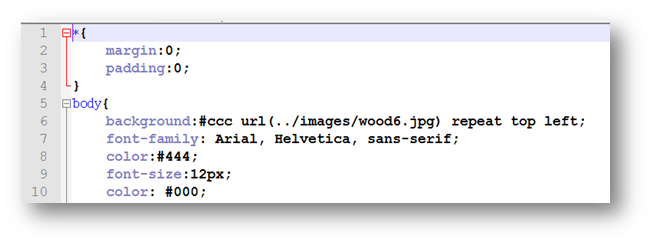 TIPO DE FUENTE
TIPO DE FUENTE
Hemos incluido nueve tipos de fuente, diferentes a la original de Moleskine, que aceptan los caracteres del español. 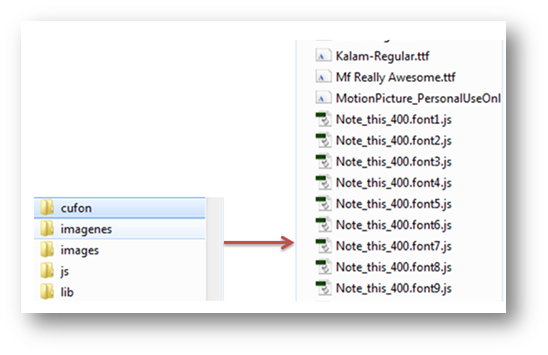 Puedes ensayar varios de ellos, modificando la línea 20 del archivo indexb.html:
Puedes ensayar varios de ellos, modificando la línea 20 del archivo indexb.html: 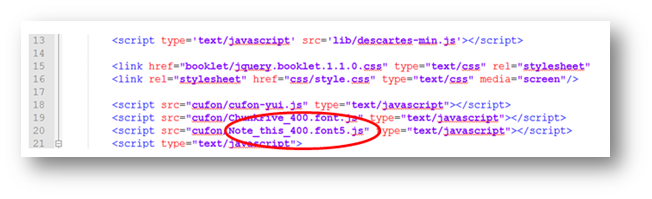 Nosotros, hemos usado la fuente Note_this_400.font5.js.
Nosotros, hemos usado la fuente Note_this_400.font5.js.
PRIMERA PÁGINA
 Por defecto, Moleskine deja en blanco la página de la contraportada. Nos ocuparemos, entonces, de diseñar la primera página. Antes de iniciar con la primera página, es importante que sepas que cada página está incluida en un bloque <div>. Nuestra primera página podemos crearla de dos formas. La primera, puede ser una imagen de un texto que diseñemos en un editor gráfico (PowerPoint, por ejemplo), un ejemplo de ello lo veremos en la segunda página. La segunda, es usar las etiquetas de HTML, así:
Por defecto, Moleskine deja en blanco la página de la contraportada. Nos ocuparemos, entonces, de diseñar la primera página. Antes de iniciar con la primera página, es importante que sepas que cada página está incluida en un bloque <div>. Nuestra primera página podemos crearla de dos formas. La primera, puede ser una imagen de un texto que diseñemos en un editor gráfico (PowerPoint, por ejemplo), un ejemplo de ello lo veremos en la segunda página. La segunda, es usar las etiquetas de HTML, así: 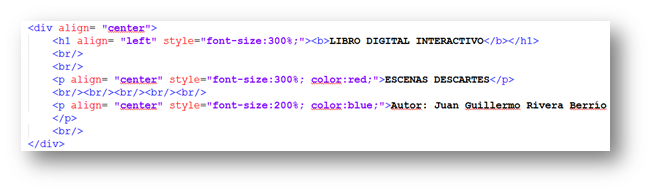 En el diseño hemos usado:
En el diseño hemos usado:
- Centrado de página: <div align= "center">.
- Etiqueta <h1>. Moleskine incluye, para esta etiqueta, un subrayado informal (ver imagen). Por ser la primera página, hemos aumentado tres veces el tamaño de la fuente usando style="font-size:300%;" y alineado el texto a la izquierda.
- Etiqueta <p>. Tiene el mismo efecto de <h1>, pero sin el subrayado. Aquí hemos usado diferentes tipos de color de fuente.
- Salto de línea <br/>.
Si no deseas usar el tipo de fuente, puedes combinar con las etiquetas <h2>, <h3>,… Si no deseas usar ninguna etiqueta, siempre te queda la opción de la imagen, como veremos a continuación.
PÁGINA CON IMAGEN
 Se trata de una imagen, que podemos incorporar así:
Se trata de una imagen, que podemos incorporar así:  Es importante tener en cuenta que su ancho y alto no puede ser superior a 450 pixeles.
Es importante tener en cuenta que su ancho y alto no puede ser superior a 450 pixeles.
PÁGINAS CON ESCENAS DESCARTES
Aquí terminamos nuestro tutorial, explicando cómo insertamos una escena Descartes. 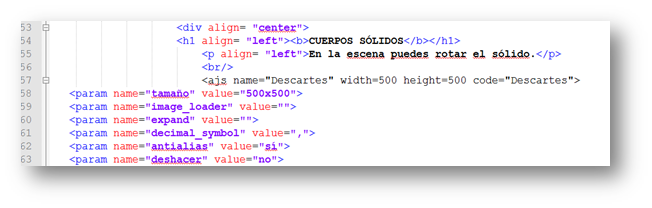 Nuestra escena debe tener un tamaño no superior a los 500x500 pixeles. Ocasionalmente, en escenas ya diseñadas, podríamos extendernos a 550x550, sacrificando un poco las márgenes de la página. Para incluir nuestras escenas al libro, seguimos este procedimiento:
Nuestra escena debe tener un tamaño no superior a los 500x500 pixeles. Ocasionalmente, en escenas ya diseñadas, podríamos extendernos a 550x550, sacrificando un poco las márgenes de la página. Para incluir nuestras escenas al libro, seguimos este procedimiento:
- Abrimos con el editor de textos el archivo de la escena Descartes.
- Copiamos el código comprendido entre las etiquetas <ajs> y </ajs>.
- En un bloque <div> pegamos este código y… listo.
Sugerencias de diseño:
- Centrar la escena. Para ello, usamos <div align=”center”>.
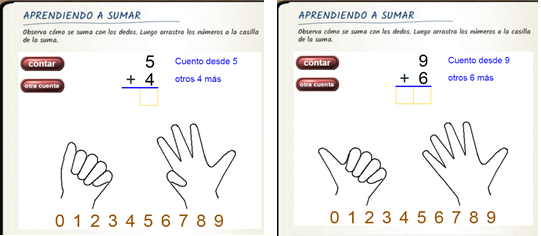
- Incluir título de la página. Podemos usar: <h1 align= "left"><b>APRENDIENDO A SUMAR</b></h1>.
- Incluir un texto introductorio. Algo así como: <p align= "left">Observa cómo se suma con los dedos. Luego arrastra los números a la casilla de la suma. </p>.
- Incluir los créditos. Además del reconocimiento al autor del libro, recomendamos incluir los créditos a la herramienta Descartes y a http://tympanus.net/codrops/2010/12/14/moleskine-notebook/, además de la licencia.
Pulsa sobre la siguiente imagen para acceder a otro libro interactivo diseñado con estas herramientas y que está publicado en el subproyecto iCartesiLibri
(Puedes descargar este libro desde este enlace)
En este artículo se muestra el proceso de comunicación entre una escena de Descartes y una página web que integra un mapa de Google Maps. Google Maps es un servidor de aplicaciones de mapas en la web que pertenece a Google. Ofrece imágenes de mapas desplazables, así como fotografías por satélite del mundo e incluso la ruta entre diferentes ubicaciones o imágenes a pie de calle con Google Street View. La interacción entre la escena de Descartes y la página web aprovecha el manejador de eventos propuesto en el artículo "Comunicación escena-html usando DescartesJS" y la API de Google Maps Javascript para controlar las acciones del usuario.
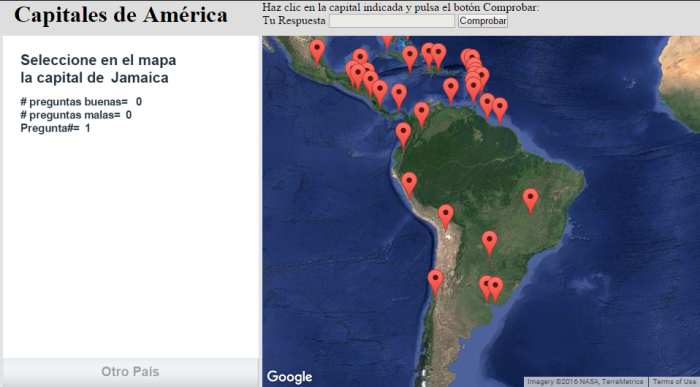
En el siguiente objeto interactivo, usado para afianzar el conocimiento de las capitales del continente americano, se propone localizar en un mapa de Google Maps la capital de un determinado país. Dicho objeto está formado por una página html que sostiene dos grandes contenedores: el primer bloque soporta una escena de Descartes embebida mediante un iframe (ubicado a la izquierda) y el segundo, un mapa de Google Maps (ubicado a la derecha).
Autor: Diego Luis Feria Gómez Red Educativa Digital Descartes Colombia
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
(Puedes descargar esta escena desde este enlace)
La comunicación entre la escena de Descartes y la página html tiene lugar en 3 momentos:
- Envío de la pregunta desde la escena de Descartes
- Gestión de la pregunta y envío de las respuesta desde el archivo html hasta la escena de Descartes.
- Administración de respuestas desde la escena de Descartes.
En la primera fase, internamente la escena de Descartes (incluida en el archivo comunicacion_Descartes.html) carga las capitales, configura las variables que controlan las respuestas del usuario y ordena los países de manera aleatoria, y después envía una pregunta a la página html en la que está embebida como iframe y que se denomina indexb.html. Este proceso es controlado por el código javascript incluido en comunica.js.
En la segunda etapa, la página indexb.html administra la interacción del usuario con el mapa y envía la respuesta a la escena de Descartes a través de el código javascript externo incluido en mapa.js. Este documento también es responsable de la construcción y configuración del mapa.
Finalmente, en la fase tercera, la escena de Descartes valida los resultados, controla los aciertos y desaciertos, y a continuación reinicia el ciclo con una nueva pregunta.
Este mes vamos a comentar una unidad de 1ºESO correspondiente a Múltiplos y divisores
en este video hemos tratado estos apartados:
1.Múltiplos y divisores
Múltiplos de un número
La división exacta
Divisores de un número
Criterios de divisibilidad
2.Números primos
Números primos y compuestos
Obtención de números primos
Descomposición factorial
3.m.c.m. y m.c.d.
El mínimo común múltiplo
Obtención del m.c.m.
El máximo común divisor
Obtención del m.c.d.
4.Aplicaciones
Problemas de divisibilidad
Más...
Misceláneas. La Proporcionalidad
Escrito por Ildefonso Fernández TrujilloProporcionalidad. Las Espirales IV
Entre las innovaciones producidas en el ámbito de la Red Educativa Digital Descartes y gracias al convenio de colaboración con la Facultad Regional Santa Fe de la Universidad Tecnológica Nacional de Argentina, está la miscelánea: Simulador de Sistemas diferenciales autónomos y no autónomos creada por la profesora Valeria Bertossi. La siguiente imagen enlaza con la miscelánea.
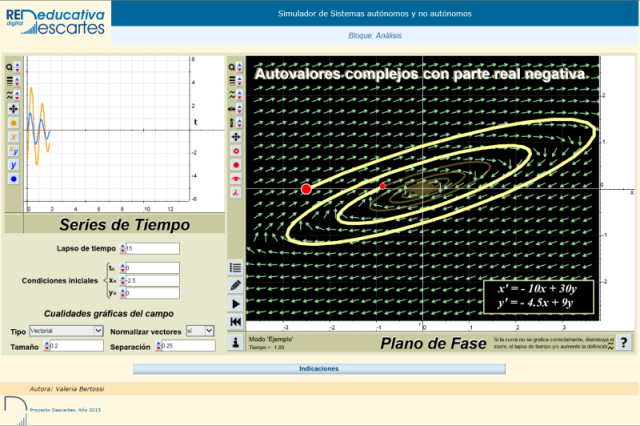
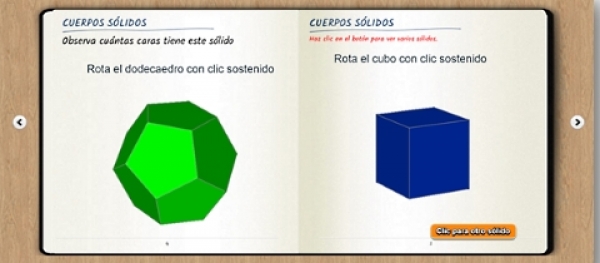
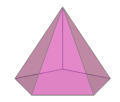
También cabe destacar la aportación del profesor José R. Galo Sánchez con su trabajo sobre Geometría tridimensional, también disponible en catalán gracias a la profesora Monserrat Gelis Bosch, que enlazamos a continuación.
En próximos artículos comentaremos y/o enlazaremos la espléndida colección de libros dinámicos, interactivos y multimedia del subproyecto iCartesiLibri que los profesores: Juan Jesús Cañas Escamilla, José R. Galo Sánchez, Juan Guillermo Rivera Berrío, Irma Manuela Benitez, Alicia Elena Carbonell y María Alicia Gemignani han creado sobre algunos temas de Estadística y Análisis. Por su indudable interés se aconseja visitar dicho subproyecto al igual que el recientemente elaborado por: José Luis Abreu León (Instituto de Matemáticas), Joel Espinosa Longi (Instituto de Matemáticas), Deyanira Monroy Zariñán (LITE) y equipo para Primaria, y que con el nombre @prende proporciona a los alumnos un material lúdico e interactivo que facilitará de forma notable la asimilación de conceptos matemáticos.
Seguimos insistiendo en la necesidad de estar al día de las posibilidades operativas y de uso de los materiales y escenas de la Red Educativa Digital Descartes. Aconsejamos acudir a los foros y contenidos de la Documentación técnica de la herramienta de autoría DescartesJS, en especial a estos, que llevan a la información sobre las familias 3D, elaborada por el profesor Juan Guillermo Rivera Berrío.
Antes de comenzar con el análisis de la escena de la espiral de Teodoro para incluirla en la miscelánea sobre las espirales en estudio, vamos a mostrar un vídeo que relaciona la música y las espirales con objeto de apreciar diferentes formas de enfocar el tema que nos ocupa.
Continuamos con la creación de la miscelánea que con el título Las Espirales va a contener una serie de escenas donde se introducirán, estudiarán y representarán algunas espirales.
En el artículo anterior terminamos de estudiar el proyecto de miscelánea tal como está en la actualidad, indicando que íbamos a integrar en el mismo el contenido de la escena de la espiral de Teodoro.
La escena de la espiral de Teodoro, que vemos a continuación
Está formada por:
- dos controles tipo pulsador
- un texto
- un punto rojo de referencia
- una familia de 139 puntos
- otra de 138 segmentos.
Los pulsadores controlan, respectivamente, la cantidad de puntos y segmentos que están presentes en la escena. Inicialmente son visibles 0 segmentos y 29 puntos.
Con objeto de que puedan verse varias vueltas de la espiral, la escala del espacio donde se representa tiene un valor de 15 en lugar de 48 que es el que viene por defecto.
Para poder dibujar la colección de puntos, y posteriormente los respectivos segmentos, hemos definido:
- Un vector de 140 de tamaño para albergar los arcos que los segmentos que unen los sucesivos puntos con el de referencia forman con la horizontal.
- Una función, x1, para controlar la abscisa de los puntos.
- Otra función, y1, para controlar la ordenada de los puntos.
Los gráficos siguientes muestran como se ha hecho lo anterior.
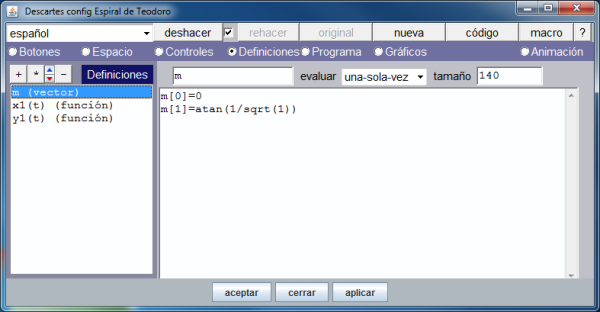
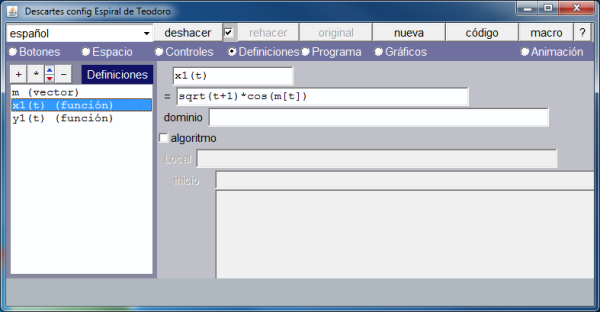
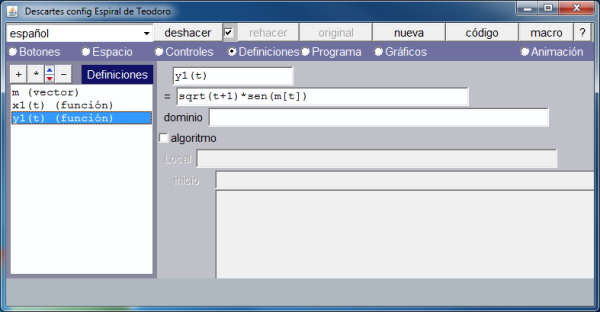
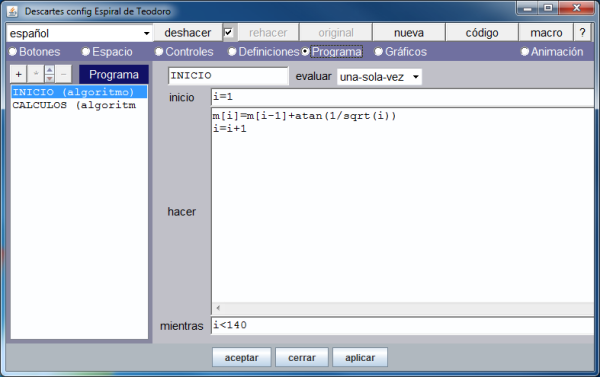
En la imagen que muestra la definición del vector se ve que únicamente se asignan valores a sus dos primeras componentes. Activando la opción de menú: Programa, vemos, en la siguiente imagen, como se han definido el resto de los arcos.
La siguiente imagen muestra los gráficos de la escena, en concreto despliega la forma en que se ha definido la colección de puntos.
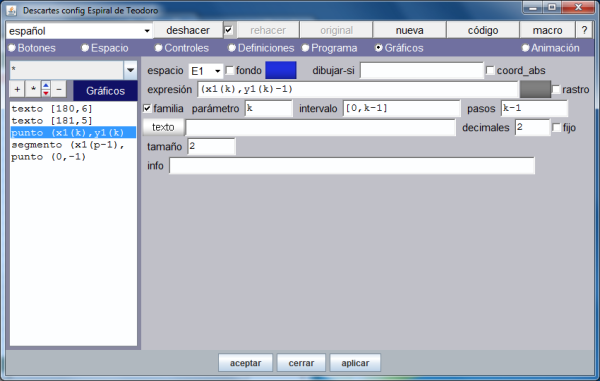
Observamos que los 139 puntos de la espiral se han definido mediante una familia que depende del parámetro k (identificador del pulsador de nombre: puntos presente en la pantalla).
La cantidad de puntos en pantalla depende del valor de este pulsador, el cual podemos manipular a nuestra conveniencia.
Analizada la escena de la espiral de Teodoro podemos pasar a incluirla en la miscelánea que estamos elaborando, acción que dejamos para el siguiente artículo. Aunque, insistimos, es conveniente que, para practicar con el editor de escenas, cada cual lo intente por su cuenta ya que disponiendo de las escenas se puede analizar cada uno de los cambios que se hagan y observar el efecto de cualquier modificación y así aprender a configurar escenas con el editor.
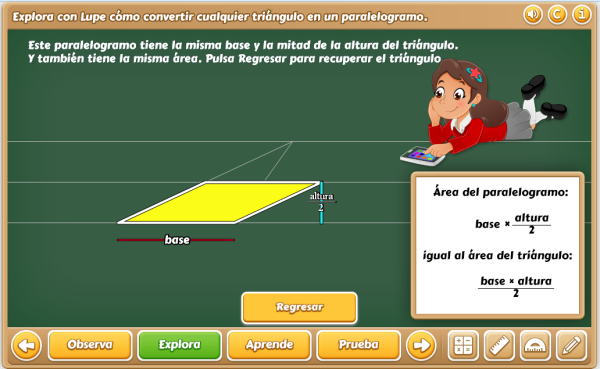
Como aplicación de la proporción Humana hemos elaborado la siguiente escena donde se hace una breve introducción al estudio del Triángulo Cordobés.
También, en la misma dirección, hemos creado, con el programa GeoGebra, una breve aplicación que muestra como teselar un cuadrado con triángulos cordobeses.
Acceso al recurso en GeoGebra
Conviene desplazar el deslizador tesela con las flechas del teclado.
En próximas entradas continuaremos con el paso a paso de la escena incluyendo la espiral Cordobesa entre sus funcionalidades, analizando el subproyecto Misceláneas, y las nuevas posibilidades que el código ofrece.
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo
Escenas con DescartesJS: Técnicas y trucos.
Escrito por Ángel Cabezudo Bueno
Abrimos esta nueva sección del Blog que hemos titulado genéricamente "Escenas con DescartesJS: Técnicas y trucos" con una escena propuesta por nuestro compañero cartesiano Eduardo Barbero Corral y contamos con él para que nos siga mostrando sus técnicas y trucos en sucesivas ediciones de esta sección del blog. Una muestra de sus habilidades para el desarrollo de escenas de Descartes puede ser consultada en el siguiente enlace al artículo "Recomendaciones, indicaciones y elementos prefabricados" que está publicado en la "Documentación técnica y de usuario de Descartes 5" (en lo sucesivo "Documentación técnica").
Las "técnicas y trucos" que se irán explicando en sucesivos artículos tendrán dos niveles, uno básico y otro avanzado. Con el nivel básico pretendemos acercar la herramienta DescartesJS a quien le pueda interesar iniciarse en la programación de escenas. El nivel avanzado estará orientado a quien ya tiene cierto dominio de la herramienta y facilitará la interpretación de las instrucciones que se incluyen en los diferentes paneles del Editor de Escenas y que nadie ignora, a veces resultan difíciles de comprender sin la correspondiente documentación del programa.
otro avanzado. Con el nivel básico pretendemos acercar la herramienta DescartesJS a quien le pueda interesar iniciarse en la programación de escenas. El nivel avanzado estará orientado a quien ya tiene cierto dominio de la herramienta y facilitará la interpretación de las instrucciones que se incluyen en los diferentes paneles del Editor de Escenas y que nadie ignora, a veces resultan difíciles de comprender sin la correspondiente documentación del programa.
Pretendemos que esta sección esté abierta a cualquier "cartesiano" que quiera comunicar alguna "técnica o truco" para resolver escenas con DescartesJS. Siempre estamos dispuestos a aprender y a recibir el estímulo de los demás.
En este supuesto poneros en contacto conmigo y acordaremos las condiciones para su publicación en este blog.
Un primer contacto con DescartesJS: Programación de una escena paso a paso
Eduardo me entregó la idea de esta escena y el proceso que él sigue en su realización que seguidamente vamos a documentar. También puso unas notas sobre lo que considera necesario preparar de antemano y los retoques y mejoras que cabe hacer con la escena.
Con todo esto, mi trabajo como redactor de este artículo ha consistido en elaborar la escena siguiendo sus pautas e interpretar sus propuestas de mejora. He ido observando todo lo que sería conveniente añadir, explicaciones e imágenes tomadas directamente de la escena o de las herramientas de trabajo, para facilitar la comprensión a quien se anime a emularlo y aprender a programar.
Quizá a alguien le pueda resultar excesivo el detalle en algunas ocasiones pero hay que pensar que se trata de la primera escena para el nivel básico y pretende que el neófito o el que ha experimentado muy poco con DescartesJS tenga la orientación suficiente para dar los primeros pasos, no se despiste demasiado y le estimule a seguir practicando. Espero haber acertado en mi pretensión.
Es importante que las explicaciones que aquí damos se acompañen, si fueran insuficientes, con la consulta puntual del concepto que se esté aportando en la "documentación técnica", sin pretender conocerlo todo desde un principio y solamente para entender la aplicación en esta escena en concreto.
Una nueva escena elaborada desde cero
Solamente comenzaremos desde cero si pretendemos elaborar una escena totalmente nueva y diferente de las que tenemos. Cuando elaboramos escenas parecidas a otras es más fácil actuar sobre la escena antigua, quitando y poniendo lo que interese, nos ahorraremos mucho trabajo.
En este caso vamos a hacer una escena totalmente nueva.
Las herramientas que se necesitan
| 1. | Un editor de texto plano (uno recomendable es Notepad++). Importante para poder consultar y si fuera el caso editar el código HTML del archivo que lleva la escena de DescartesJS. La escena se reconoce porque va entre etiquetas <ajs> y </ajs>. |
| 2. |
El Gestor de Escenas de Descartes (Descartes.jar) y la carpeta lib conteniendo el archivo intérprete descartes-min.js. |
El Gestor de Escenas está desarrollado en la "Documentación técnica" y puede descargarse desde http://arquimedes.matem.unam.mx/Descartes5/distribucion/
Crea una carpeta y nómbrala p.e. "Descartes5" para guardar esta descarga. Para abrir el Gestor de Escenas basta hacer doble clic en el nombre del archivo Descartes.jar. Es práctico tener un acceso directo a este archivo desde el Escritorio de Windows, cada vez que se quiera trabajar con él. Este es el aspecto que tiene la ventana del Gestor de Escenas cuando se abre en pantalla, mostrando por defecto una escena básica nueva.
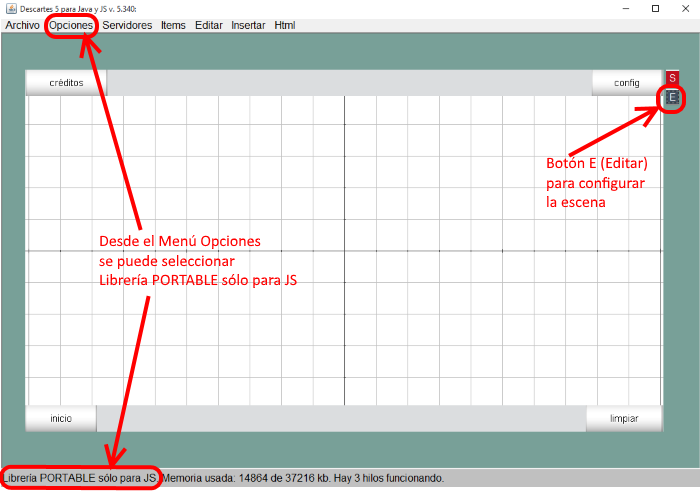
Figura 1
Una de las herramientas que nos interesa por ahora del Gestor de Escenas es el Editor de Escenas que facilita la escritura del código de la escena a través de un determinado número de paneles de configuración: Botones, Espacio, Controles, Definiciones, Programa, Gráficos y Animación.
Las escenas que vamos a explicar en esta serie de artículos son escenas de DescartesJS. El sufijo JS viene a señalar que el intérprete está escrito en JavaScript. Una escena escrita en DescartesJS necesita la referencia a un archivo llamado descartes-min.js para que pueda ser interpretada cuando se abra el archivo HTML que la contiene y se visualice en un navegador Web como Google Chrome, Mozilla Firefox o Safari de Apple. Este archivo puede ser descargado desde
http://arquimedes.matem.unam.mx/Descartes5/lib.
La imagen siguiente muestra la estructura de carpetas que va a tener nuestro proyecto.
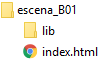
Figura 2
Para el caso de la escena que vamos a desarrollar en este artículo el archivo descartes-min.js debe de estar en la carpeta llamada lib. Esto se consigue simplemente seleccionando desde el Menú Opciones, Librería portable y solo para JS. Puede observarse que este modo está seleccionado si aparece escrito en la línea de estado de la ventana del Gestor de Escenas (Figura 1)
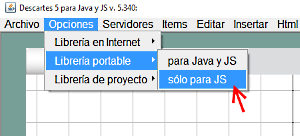
Figura 3
El archivo index.html lleva el código de la escena y la referencia al intérprete descartes-min.js (ver más adelante el apartado Preparar lo Necesario)
Idea del proyecto
|
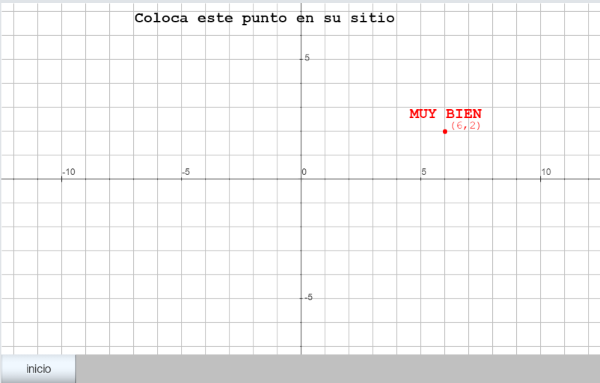
Escena_B01: Se trata de una escena para que el alumno aprenda a situar puntos sobre el plano cartesiano. Será una escena de tipo actividad, es decir que el alumno debe contestar actuando sobre la escena y el ordenador le indicará si lo hace bien o mal. Es conveniente que primero dibujemos en un papel nuestro proyecto. En la escena solamente aparecerán los ejes de coordenadas y la frase "Coloca este punto en su sitio:" Continuando la frase aparecerá el punto y entre paréntesis sus coordenadas cartesianas, empleando números enteros. Esos valores de las coordenadas serán números aleatorios para que cada vez que se inicia la escena sean diferentes. El alumno deberá mover ese punto con el puntero hasta colocarlo adecuadamente en su lugar. Cuando ese punto esté en su sitio aparecerá el mensaje "MUY BIEN ". |
La siguiente imagen lleva un enlace a la escena ya elaborada a partir de la idea expuesta. Interaccionar con ella para comprender su funcionalidad y después veremos cómo se crea el programa en DescartesJS utilizando el Editor de Escenas.
Figura 4
Preparar lo necesario
Crear una carpeta, p.e. escena_B01, que contendrá archivo HTML que se va a elaborar, p.e. index.html. En ella también debe estar la subcarpeta lib con el archivo intérprete descartes-min.js.
Esta operación puede realizarse completamente desde el Gestor de Escenas tal como indicamos seguidamente.
Una vez abierto el Gestor y seleccionada la opción Librería portable > solo para JS, se guarda desde el menú Archivo seleccionando Guardar como, que permite seleccionar la carpeta escena_B01 si ya existe o crearla en su caso y poner nombre al archivo que portará la escena p.e index.html.
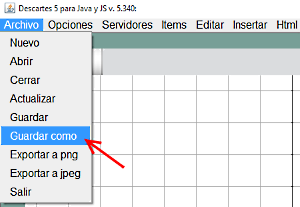
Figura 5
Dentro del archivo index.html que contiene la escena por defecto entre etiquetas <ajs> y </ajs>, el Gestor de Escenas ha colocado la línea de código <script type='text/javascript' src='lib/descartes-min.js'></script> delante de la etiqueta de cierre </head>
Para familiarizarse con estos conceptos conviene consultar el código HTML del archivo index.html para la escena básica abriéndolo con un editor de texto plano como Notepad++.
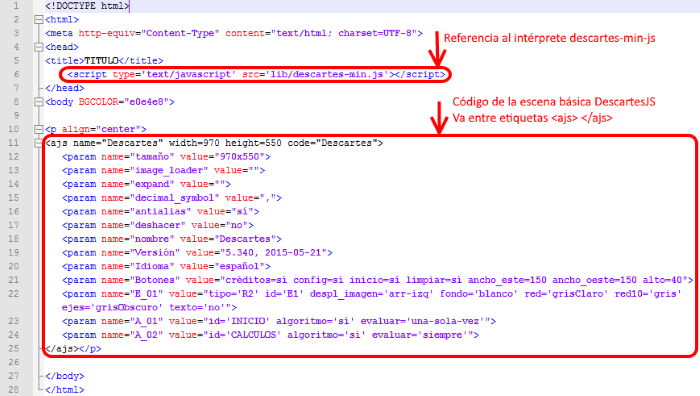
Figura 6
La escena ocupará un espacio rectangular de 800x510 píxeles. Con una unidad coordenada de 32 píxeles van a poderse ver con cierta holgura puntos (x,y), x entre -10 y 10 e y entre -5 y 5.
Al abrir el Gestor nos muestra una escena por defecto (escena básica) de dimensiones 970x550 píxeles (Figura 1). Éstas se cambian pulsando el botón E (edición) o Config y después, en el Editor de Escenas, el botón código (Figura 7) modificando los valores width (ancho) y height (alto) (Figura 8)
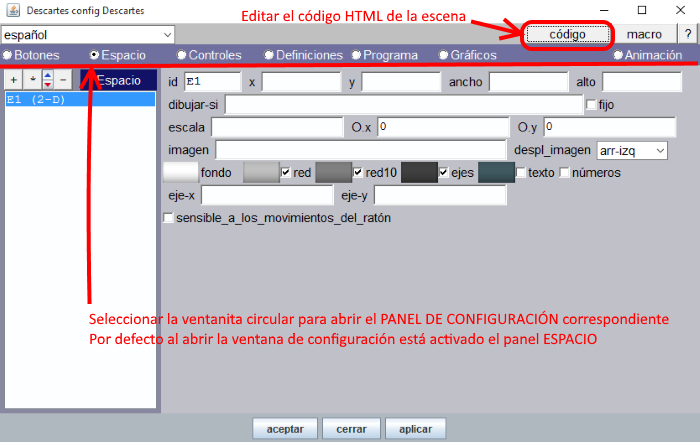
Figura 7
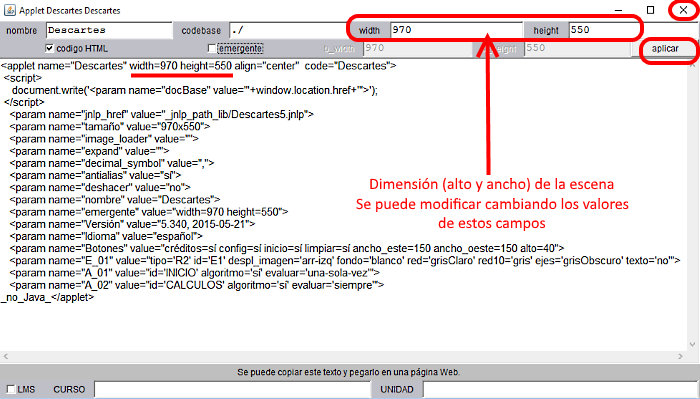
Figura 8
Para fijar el cambio se pulsa aplicar y se cierra (X) la ventana de código. Pueden verse estos cambios si pulsamos aplicar/aceptar en la ventana Descartes Config (Figura 7)
Proceso a seguir en el Editor de Escenas
| 1. |
Desde el Gestor de Escenas se accede al Editor de Escenas. Se selecciona el panel Botones y se desmarcan las casillas de créditos, config y limpiar, dejando solamente marcada la de inicio. Para que surta los efectos de este cambio hay que pulsar aplicar y aceptar para salir del editor aceptando los cambios. El botón Inicio aparecerá en el ángulo inferior izquierdo de la escena (Figura 4) y cuando se pulse repondrá la escena en condiciones iniciales del programa. |
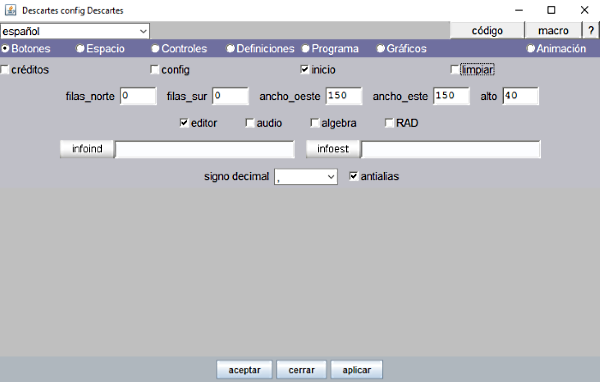
Figura 9
| 2. | En el panel Espacio, se fija una escala a 32 y se marcan únicamente las casillas para que se vea red, ejes y números. La escala es el número de píxeles que contiene la unidad coordenada. La casilla fijo, si está marcada, consigue que el espacio quede fijo y no se podrá desplazar cuando se arrastra el puntero sobre el mismo |
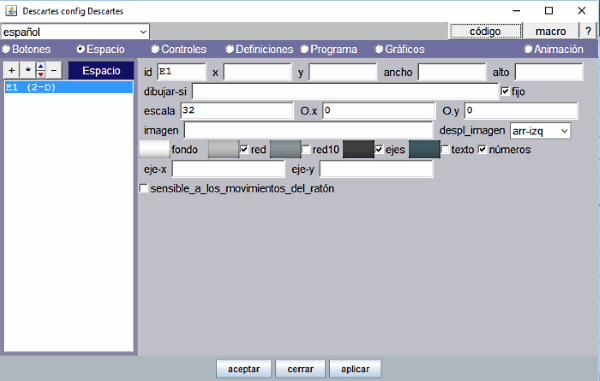
Figura 10
| 3. |
Para situar en escena la frase "Coloca este punto en su lugar" se selecciona el panel Gráficos y se añade un gráfico tipo punto de tamaño 0 y en la ventana texto se escribe esa frase. Se cambian sus coordenadas (0, 0) en la ventana expresión por (-7, 6.5) o hasta que la frase quede en el lugar que interese. Se pulsa aplicar y se comprueba que aparece en la escena. La Figura 11 siguiente, muestra el panel Gráficos con el primer punto añadido. Para añadir un gráfico en la escena hay que pulsar el botón (+) y seleccionarlo de una lista ofrecida con los diferentes tipos. Si queremos que solo aparezca este texto basta indicar que el tamaño del punto sea 0. El gráfico tipo texto en cambio situaría el texto según una expresión encerrada entre corchetes [x,y] donde x e y vienen dados en píxeles siendo el origen [0,0] el vértice superior izquierdo de la escena. |
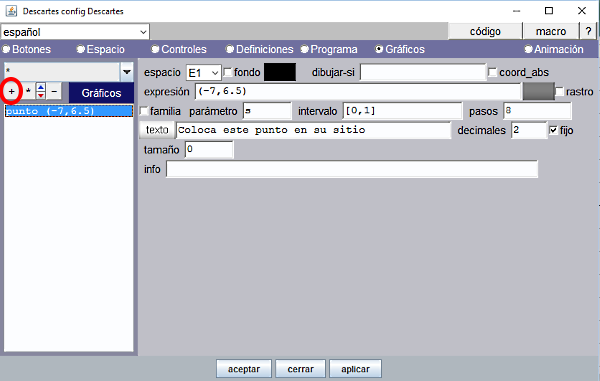
Figura 11
| 4. |
Ahora es necesario crear un control gráfico para poder referenciar sobre él un punto que podamos mover arrastrándolo con el puntero. |
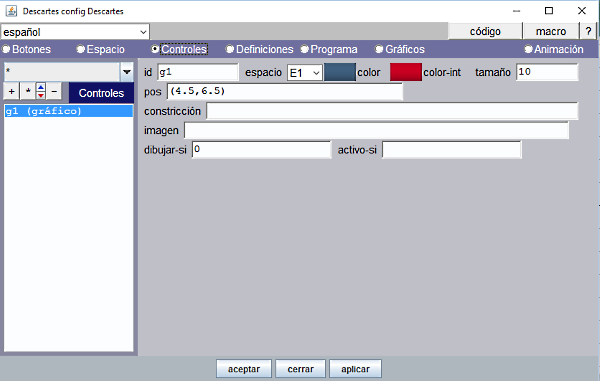
Figura 12
|
Pero el disco del control no tiene que verse, por eso debe de figurar dibujar-si=0. Esta es una condición lógica que debe de verificarse para que se dibuje el control. Al asignar el valor 0 o FALSO no se dibujará. Las coordenadas x e y del control gráfico como el g1 se pueden referenciar en cualquier parte del programa escribiendo g1.x y g1.y como vemos en el siguiente paso. |
| 5. |
En el panel Gráficos se añade un nuevo gráfico tipo punto. |
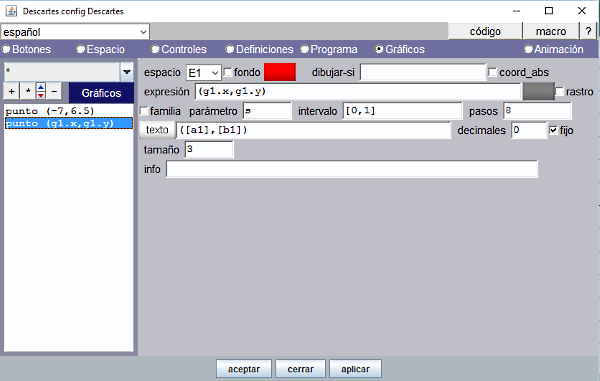
Figura 13
|
Observar que para que se escriban los valores de las variables a1 y b1 y no estos nombres hay que encerrarlos entre corchetes [a1] y [b1]. Para que no se escriban estos valores con coma decimal hay que poner 0 en la ventana de decimales. |
| 6. |
Estos valores auxiliares a1 y b1 se definen en el panel Programa. Puede hacerse en el algoritmo INICIO que se calcula solo una vez, escribiendo en el campo hacer, a1=ent(rnd*21)-10 En a1 se obtiene un valor aleatorio entero comprendido entre -10 y +10. Observar que rnd es una función interna de Descartes que genera un valor dentro del intervalo [0, 1). |
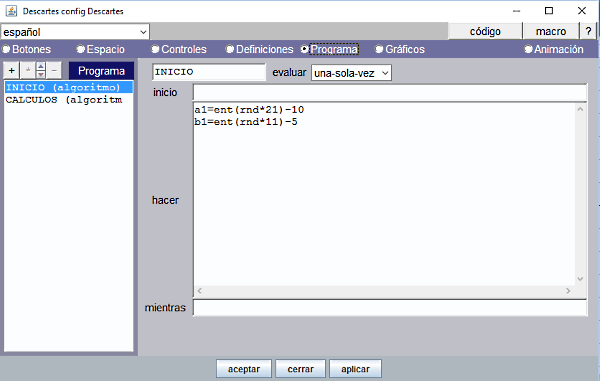
Figura 14
|
Es conveniente Guardar desde el menú Archivo cada vez que hemos completado un proceso, para que no se pierda nuestro trabajo en caso de que surja algún problema con el ordenador. |
| 7. |
Queremos que el programa compruebe que el alumno, cuando interacciona con la escena, coloca el punto en su sitio y que entonces aparezca un mensaje indicando que está bien. Para ello debemos definir un auxiliar en el panel Programa, en el algoritmo CÁLCULOS y que se evalúe siempre: bien1= (abs(a1-g1.x)<0.1)*(abs(b1-g1.y)<0.1) bien1 es el resultado de multiplicar 2 expresiones que únicamente pueden valer 0 ó 1. Es necesario darle un pequeño margen 0.1 porque sino sería muy difícil acertar. Esta fórmula comprueba que las coordenadas en que se coloca el punto son las mismas que las del control gráfico, (g1.x, g1.y). Si el punto está en el lugar adecuado, entonces bien1 valdrá 1. |
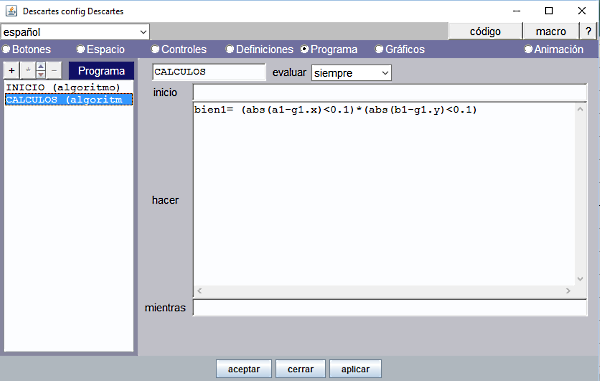
Figura 15
| 8. |
Falta añadir en el panel Gráficos un tercer punto, de tamaño 0, con el texto "MUY BIEN"; poniendo la condición dibujar-si=bien1. Es decir el texto se escribe cuando bien1 toma el valor 1 o VERDADERO. |
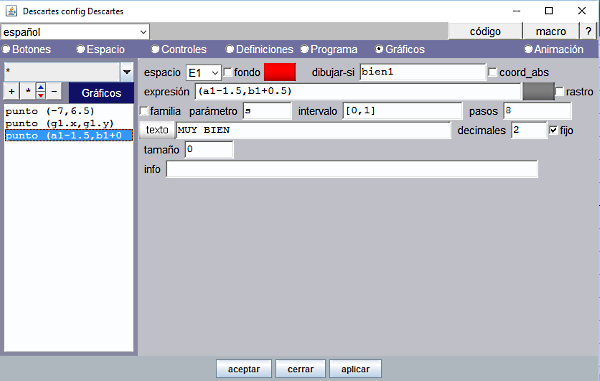
Figura 16
|
Conforme se ha ido elaborando la escena se comprueba que todo funciona y aparece lo que se quiere. |
| 9. |
Finalmente, hay que Guardar y Cerrar desde el menú Archivo del Gestor de Escenas. |
Retoques y mejoras
Todas excepto la última de las que se indican se han tenido en cuenta al describir el proceso anterior.
| 1. | El tamaño de la escena por defecto es muy grande. Para modificar el tamaño de la escena, se hace desde el código fuente, cambiando los números que aparecen inicialmente y que indican el ancho y el alto de la escena. |
| 2. |
Modificaciones en el panel espacio. Conviene que la escala sea la deseada y que no se pueda arrastrar el espacio con el puntero, por ello en el panel espacio se marca la casilla fijo. No deben de verse las coordenadas del puntero al hacer clic izquierdo, para ello se deja desmarcada la casilla texto. |
| 3. | Es conveniente que el color, el tipo y el tamaño de la letra sea lo adecuado. En este trabajo se da formato a los textos utilizando la opción Texto simple
, al pulsar el botón texto,
que permite cambiar algunos atributos básicos, tales como el tipo de letra, tamaño, negrita y cursiva. La otra opción Texto con formato dispone de un repertorio más amplio y se podrá ver en sucesivos trabajos. |
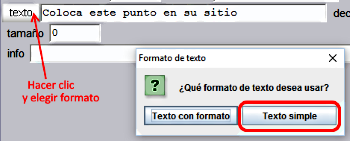 Figura 17 Figura 17
|
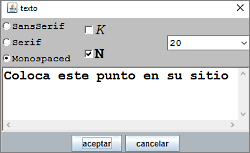 Figura 18 Figura 18
|
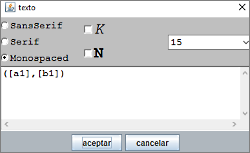 Figura 19 Figura 19
|
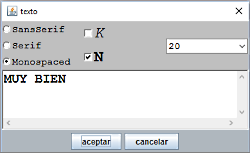 Figura 20 Figura 20
|
| Se habrá podido observar como el color del punto que debe ser movido y el texto "MUY BIEN" llevan color rojo. Hemos visto que la opción Texto simple no dispone del atributo color; en este caso el color del texto puede modificarse utilizando el botón de color (1) que figura en el panel Gráficos. Al pulsar el botón de color (1) se abre una ventana que facilita le selección del color, bien a través de un listado de colores estándar (2), o mediante una combinación cualquiera de valores hexadecimales desde 00 a FF para cada uno de los tres colores básicos rojo verde y azul. |
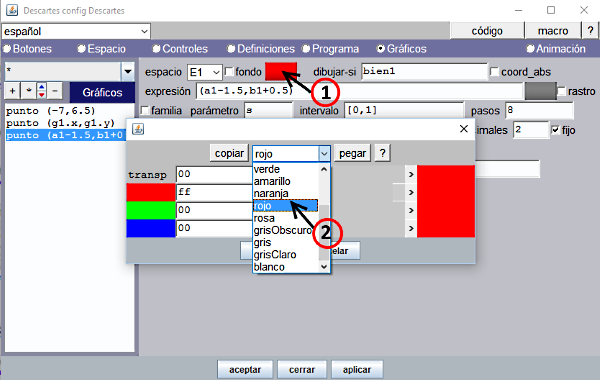
Figura 21
| 4. | En la frase del principio "Coloca este punto en su sitio" y en "MUY BIEN " no interesa que se vea el punto del texto, por eso ponemos tamaño=0. |
| 5. | Una posible mejora se consigue poniendo en la escena varios puntos para situar correctamente en el plano cartesiano en vez de uno solo y también los auxiliares necesarios para ello. No obstante, es mejor que la escena no quede recargada y que todo ello tenga un aspecto simple. |
Autoría:
Eduardo Barbero Corral (Idea del proyecto y técnicas de programación DescartesJS)
Ángel Cabezudo Bueno (Interpretación, edición de la escena, ilustraciones y redacción)
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)





 CONTACTO
CONTACTO
