Esta semana vamos a ver cómo insertar en nuestro blog un objeto digital de la Red Educativa Digital Descartes.
Hemos seleccionado una actividad de cálculo con fracciones para 1º de la ESO, que pertenece a la unidad Fracciones del Proyecto ED@D. Esta actividad es autocorrectiva y permite al estudiante practicar y consolidar el cálculo con operaciones combinadas de fracciones. Se proponen diferentes tipos de ejercicios que el estudiante deberá realizar correctamente ya que en caso contrario no podrá pasar a la siguiente operación.
Para insertar dicho objeto digital en una página de nuestro blog, activaremos la edición en HTML y pegaremos el código para abrir en una ventana emergente.
En el apartado materiales del blog de la Red podemos encontrar el código para insertar de la mayoría de actividades. En caso de no disponer del código deberemos actualizarlo escribiendo la dirección web de nuestro recurso y comprobar las dimensiones de la escena. También necesitaremos una imagen desde la cual abrir el recurso. Podemos seleccionar una imagen de la misma unidad (copiando la ruta del enlace) o cualquier otra imagen ya sea desde nuestro ordenador, subiéndola directamente al blog, o desde algún álbum virtual (por ejemplo Picasa).
Continuando la serie de la Aplicación de juegos didácticos vamos a comentar Evitar hundirse.
Se trata de un juego que consta de doce preguntas con cuatro opciones cada una. Si el alumno adivina la respuesta se anota un acierto pero si falla recibe una penalización. Ese castigo consiste en una masa que irá haciendo que vaya hundiendo y termine perdiendo si falla demasiado.
Para hacerlo más divertido el valor de la masa no es fijo sino que es un número aleatorio entre 100 y 500 kg. Si llegamos a 1000 kg de penalización estaremos eliminados. Este componente de suerte sirve para igualar un poco las posibilidades de todos los participantes.
Una vez que termina un alumno podemos dar por finalizada la partida o que empiece el siguiente. El juego contiene un marcador que registra la puntuación de hasta veinte alumnos lo que fomenta la competitividad.
En el marcador veremos quién se ha salvado y quién no. En él podremos comprobar cuántos aciertos han logrado cada uno y cuantos kilos han recibido como "recompensa" a sus errores.
Entre las versiones del juego encontramos:
Para utilizar sin preocuparnos de los ficheros de preguntas
Pues eso, para jugar
- Juego con preguntas en ficheros:
Para cargar los ficheros disponibles o los que generemos con las preguntas que nos interese hacer.
Como siempre, también disponemos de varios idiomas para la interface del juego.
Aquí tenéis un vídeo que repasa de forma gráfica muchas de la opciones que nos ofrece el juego:
Si os interesa también lo podéis descargar desde este enlace.
Esperamos que os sea útil.
Ya sabéis que en la Red Descartes disponéis de muchos más recursos
Entrevista al personaje misterioso (XII)
Escrito por Eva M. Perdiguero Garzo Hoy nos visita en nuestra radio, un hombre que no sólo fue MATEMÁTICO sin que también se distinguió por su ávida curiosidad, su ingenio como inventor y su agudeza mental para vencer al más temible de los ejércitos de su época o desenmascarar a todo aquel que quiso apropiarse de alguno de sus descubrimientos. Con este personaje cerramos la serie que hemos estado emitiendo durante casi un año sobre personajes matemáticos, ilustres en la historia.
Hoy nos visita en nuestra radio, un hombre que no sólo fue MATEMÁTICO sin que también se distinguió por su ávida curiosidad, su ingenio como inventor y su agudeza mental para vencer al más temible de los ejércitos de su época o desenmascarar a todo aquel que quiso apropiarse de alguno de sus descubrimientos. Con este personaje cerramos la serie que hemos estado emitiendo durante casi un año sobre personajes matemáticos, ilustres en la historia.
Escucha atentamente el podcast que puedes ver más abajo y déjanos tu comentario sobre quién crees que es este misterioso personaje. La semana que viene publicaremos su identidad a través de un puzle.
En la interpretación de nuestro personaje misterioso tenemos a nuestro compañero: Bernat Ancochea Millet. Profesor de matemáticas y director del INS Premià de Mar.
El guión es obra de Eva M Perdiguero profesora de matemáticas y socia colaboradora de Red Educativa Digital Descartes. El trabajo lleva licencia CC BY-NC-SA 4.0. La entrevistadora y realizadora del podcast, también es Eva M Perdiguero.
Tanto los efectos especiales como la imagen del comienzo del artículo, pertenecen al Banco de sonidos del INTEF-MECD-ESPAÑA, tienen licencia CC BY-NC-SA 3.0 y han sido adaptados para esta ocasión.
Este mes vamos a retomar el primer curso de la ESO, para eso vamos a ver la unidad correspondiente a números naturales:
En la exposición recordamos la existencia de las versiones en PDF y así como de los cuadernillos de trabajo. El esquema del tema es el siguiente:
1.Números naturales
Sistema de numeración decimal
Escritura
Orden y redondeo
2.Operaciones
Suma y resta
Multiplicación y división
Jerarquía de las operaciones
3.Potencias
Con exponente natural
Propiedades
4.Raíces cuadradas
Raíz cuadrada exacta
Raíz cuadrada entera
5.La calculadora
Estándar
Científica
Más...
En el acercamiento superficial que estamos haciendo al editor de ecenas aún no hemos mencionado nada acerca de la inserción de sonido, vídeo y animaciones en las utilidades que podemos crear. En este artículo vamos a mostrar una escena con animaciones y veremos como se configuran y la manera de ejecutarlas.
La opción Animación está en la barra del menú principal del Editor de Escenas Descartes, en la parte derecha, según podemos observar en el siguiente gráfico donde se muestra la opción ya desplegada con las animaciones de la escena definidas. En nuestro caso al desplegar la opción, esta presenta el siguiente aspecto:
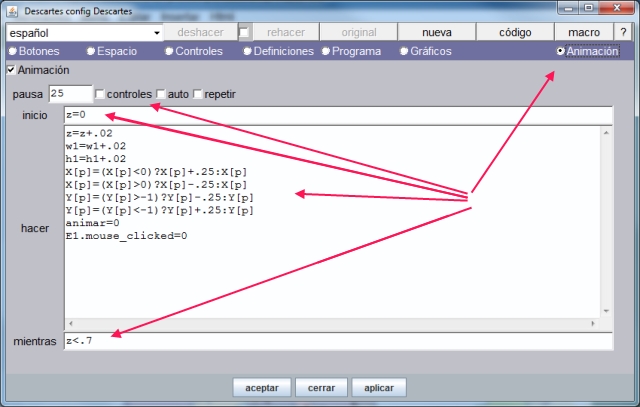
Es conveniente analizar el gráfico anterior detenidamente. Corresponde a la definición de las animaciones (tres) de la utilidad. Se observan dos regiones: la parte superior, zona donde se configura el comportamiento genérico de la animación y la parte inferior donde se define el algorítmo que la controla. El significado y uso de pausa, controles, auto y repetir se explica en la documentación técnica y de usuario de Descartes v5.
Como observamos en el siguiente vídeo la escena cuenta con tres animaciones, la de los simbolos de acierto y fallo, la del muñeco que lamenta el fallo y la del gráfico de la ciudad que ocurre cuando la respuesta es correcta.
En el primer gráfico vemos que las animaciones están controladas por la variable z que es de la que depende la anchura de la imagen que se desplaza y crece; o simplemente crece según se muestra a continuación.
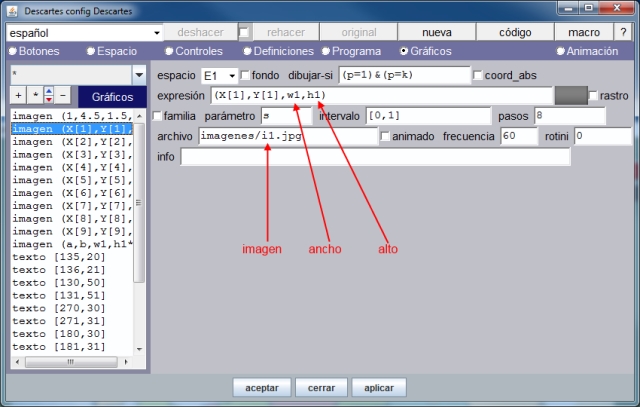
En el vídeo hemos visto el ejemplo para Europa de la creación de Juan Guillermo Rivera Berrío, a la que ha denominado GEOcultura, y que se integra dentro del proyecto GEOgráfica. Ya están desarrollados, aunque en fase beta, los contenidos para América, Suramérica, Europa, Asia y África y en proceso está Oceanía. El siguiente enlace nos lleva a parte del desarrollo de la utilidad para Europa, donde podemos observar las variantes respecto a la forma y la dinámica del enfoque primitivo.
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
En siguientes entradas continuaremos analizando el subproyecto Misceláneas, y las nuevas posibilidades que el código ofrece.
Ildefonso Fernández Trujillo
Descartes en la Universidad. Miscelánea: Proyección sobre planos coordenados
Escrito por Elena Álvarez SáizAcceso a la miscelánea: Proyección sobre planos coordenados
En esta miscelánea se muestra cómo proyectar puntos y superficies sobre planos coordenados.
Por defecto, en la escena aparece la proyección de un punto sobre el plano z=0. Sin embargo, también es posible proyectar triángulos y ciertas superficies sobre los tres planos coordenados XY, YZ y XZ.
La proyección de un punto P sobre cualquier plano es aquel punto del plano que se encuentra a distancia mínima de P.
Para proyectar un triángulo T bastará considerar el formado por la proyección de los vértices de T y en el caso de una superfice, su proyección se obtendrá proyectando todos sus puntos. Elegida la opción superficies, la escena permite practicar con porciones de paraboloides o cilindros intersecados por un plano vertical que se encuentran en el primer octante.
En la propia escena se ha incluido un botón con instrucciones que aclaran cómo utilizar esta miscelánea.
Acceso a la miscelánea: Proyección sobre planos coordenados
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)



 CONTACTO
CONTACTO
