Mostrando artículos por etiqueta: rectas
Las curvas regladas son curvas que se pueden generar a partir de una familia de rectas (segmentos) que se intersecan. El uso de las curvas regladas y, por extensión, las superficies regladas, se aplica en muchos campos de la ciencia y la tecnología, siendo de especial interés en el mundo de la ingeniería y arquitectura.
En este artículo se presenta una serie de actividades con ejemplos sencillos de curvas regladas. Las unidades seleccionadas pertenecen al Proyecto Misceláneas de la RED Descartes y en ellas se pretende introducir al alumnado en el mundo del diseño de las curvas regladas.
Unidades seleccionadas:
En esta primera escena se presentan cuatro ejemplos de curvas regladas. Siguiendo las instrucciones que se indican en cada caso, se puede proponer al alumnado que aplique estos conceptos en papel cuadriculado y diseñe sus propias creaciones.
En esta segunda escena se muestran tres nuevos ejemplos. Una vez visionados todos los ejemplos se propone la realización de estas actividades en papel cuadriculado o con clavos e hilos sobre una plancha de madera con la técnica denominada hilorama.
En la escena se cuenta con cuatro controles gráficos que determinan una familia de segmentos. El desplazamiento de esos controles conllevará la visualización de múltiples curvas regladas.
Postales navideñas. Dibujar curvas con rectas
Escena con tres ejemplos sencillos de dibujos con motivos navideños formados a partir de curvas regladas.
Como actividad antes de las vacaciones, podemos animar a los estudiantes para que diseñen sus propias creaciones navideñas.
Título: Puzle de fórmulas de Geometría
Sección: Plantillas
Bloque: Aplicaciones
Unidad: Matemáticas - Geometría
Nivel/Edad: 4º ESO (15 o más años)
Idioma: Castellano
Autora: Montserrat Gelis Bosch
![]() Haz clic en la imagen para abrir una muestra de este recurso
Haz clic en la imagen para abrir una muestra de este recurso
Puedes encontrar todas las plantillas en
https://proyectodescartes.org/plantillas/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
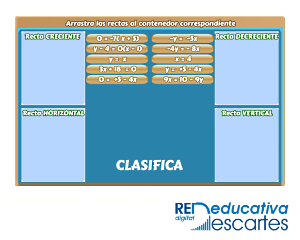
Título: Clasificar rectas por su pendiente
Sección: Plantillas
Bloque: Aplicaciones
Unidad: Análisis-Funciones elementales
Nivel/Edad: 3º ESO (14 o más años)
Idioma: Castellano
Autoría: Rita Jiménez Igea
![]() Haz clic en la imagen para abrir una muestra de este recurso
Haz clic en la imagen para abrir una muestra de este recurso
Puedes encontrar todas las plantillas en
https://proyectodescartes.org/plantillas/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
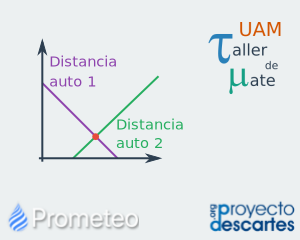
Título: Intersección de rectas
Sección: Prometeo
Bloque: Geometría
Unidad: Geometría analítica plana
Nivel/Edad: Bachillerato y Universidad (17 años en adelante)
Idioma: Castellano
Redacción: Alejandro Radillo Díaz
Programación: Alejandro Radillo Díaz
Diseño gráfico: Said David Nájar Gil
![]() Haz clic en la imagen para abrir el recurso
Haz clic en la imagen para abrir el recurso
Puedes encontrar todos los materiales del Proyecto Prometeo en https://proyectodescartes.org/Prometeo/index.htm - Ver Créditos
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Posiciones relativas de recta y circunferencias
Sección: Plantillas
Bloque: Aplicaciones
Unidad: Matemáticas - Geometría
Nivel/Edad: 1º ESO (12 o más años)
Idioma: Castellano
Autoría: Rita Jiménez Igea
![]() Haz clic en la imagen para abrir una muestra de este recurso
Haz clic en la imagen para abrir una muestra de este recurso
Puedes encontrar todas las plantillas en
https://proyectodescartes.org/plantillas/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional
Título: Pendiente en la ecuación de la recta
Sección: Plantillas
Bloque: Aplicaciones
Unidad: Matemáticas - Análisis
Nivel/Edad: 1º ESO (12 o más años)
Idioma: Castellano
Autoría: Rita Jiménez Igea
![]() Haz clic en la imagen para abrir una muestra de este recurso
Haz clic en la imagen para abrir una muestra de este recurso
Puedes encontrar todas las plantillas en
https://proyectodescartes.org/plantillas/index.htm - Ver Créditos
Este material está publicado bajo una licencia:

Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional