Planifica el curso escolar en Infantil y Primaria con los recursos de Proyecto Descartes
Escrito por José Antonio Salgueiro GonzálezLos profesionales de la enseñanza siempre empezamos los cursos escolares con ilusión, entusiasmo y emoción, atributos que esperamos transmitir, como en años anteriores, a todos los agentes que intervienen en la educación. Por todo ello, ofrecemos el acceso gratuito a nuestros recursos para el personal docente, el alumnado y sus familias, unos recursos interactivos que han demostrado su gran utilidad tanto en la enseñanza presencial como en la enseñanza a distancia. Concretamente, en este artículo, que da comienzo a la campaña de "la vuelta al cole", ofrecemos para las etapas de Infantil y Primaria, completamente actualizado, el catálogo de recursos interactivos en HTML5 para cualquier ordenador y dispositivo móvil, con una clasificación por área o materia, esperando que desde cualquier lugar del mundo, a cualquier hora, sólos o acompañados, repercutan en una mejor formación competencial de nuestro alumnado.
Ontogenia matemática del Nautilus (II)
Escrito por José R. Galo SánchezEn su primer verticilo, la concha del Nautilus tiene un crecimiento diferenciado del que acontece en el segundo y tercero. Su esencia, implícita y explicitamente, es siempre cordobesa, pero de partida el número de cámaras en ese primer verticilo son ocho y consecuentemente con paso π/4 entre ellas, frente a las diecisés y paso π/8 del segundo, paso que también ocurre en el tercero. ¿Qué acontece en la ontogenia del Nautilus que sea la causa productora de esa distinción? En este segundo artículo (desde aquí puede acceder al primero) nos adentraremos en la biología de este animal, o más precisamente en el rastro calcáreo que deja y que conforma su concha, para tratar de dar respuesta matemática a esta pregunta. Procedamos a iniciar y a adentrarnos en la ontogenia del Nautilus y desde ahí trascender a su ontogenia matemática.
La concha embrionaria y el primer verticilo
A primera vista la concha embrionaria del Nautilus (Fig. 6), en su periodo pre-cameral, aparenta una forma similar a la concha de una lapa (Fig. 7) (MolluscaBase eds., 2021), pero a diferencia del crecimiento que sigue ésta, que simplificadamente podemos decir que es radial y anular, el Nautilus aborda un cambio de concavidad en la parte dorsal y adopta una curvatura similar tanto en la parte ventral como en la dorsal (Fig. 8) y eso es lo que marca la tendencia a la forma enrollada que adquirirá con posterioridad. La parte dorsal embrionaria es inicialmente casi plana, pero en la denominada constricción de la cicatriz (Fig. 11), coincidiendo con el inicio de la formación de las primeras cámaras y septos, es cuando se produce ese cambio de concavidad que forma el labio interior dorsal (observar en la parte inferior de la Fig. 6-D el piquito que está formándose y en las figuras 12 a 14 cómo se va desarrollando ese labio). Si no se produjera ese cambio de concavidad, irremediablemente la concha se cerraría al intersecar consigo misma. Cuando al crecer, el labio llega a confluir con la parte dorsal inicial de la concha se produce la formación del espacio umbilical u ombligo (Figura 10), momento en el que se completa el primer verticilo y, consecuentemente, la parte ventral inicial de la concha pasa ahora a ser interior a la misma y comienza a actuar como nueva parte dorsal de la cámara habitacional en el segundo verticilo.
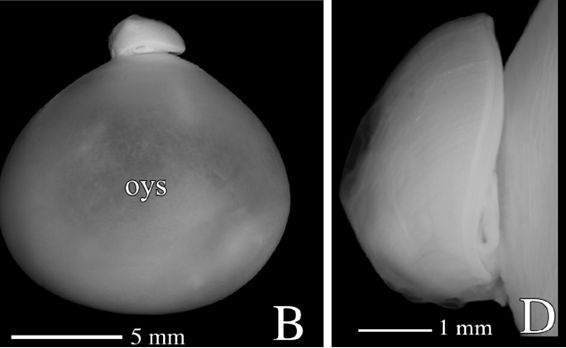
Fig. 6. Embrión de 4 meses del Nautilus pompilius. Imagen B: Perfil con el saco vitelino exterior (oys: outer yolk sac). Imagen D: Detalle de la concha embrionaria. (Procedente de Sasaki, et al., 2010).

Fig. 7 Lapa (Patella). Muséum national d’Histoire naturelle, Paris (France).
 |
 |
|
Fig. 8. Embrión del Nautilus belauesis dentro de la cápsula del huevo (éste ha sido recortado en la parte superior. El embrión contaba con una cámara septal. Procedente de Saunders and Landman (2010: pl. IV, p. xxxiv) |
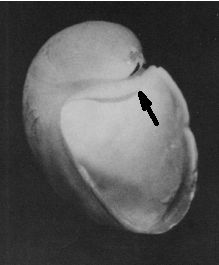
Fig. 9. Labio dorsal (señalado por la flecha) en la concha del Nautilus en la fase de dos cámaras. (Procedente de Landmam et al.1989). |
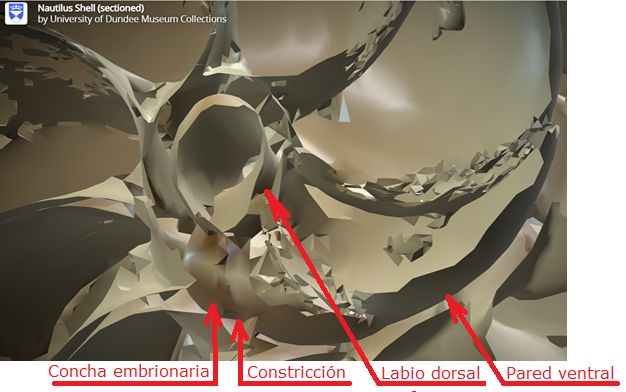
Fig. 10. Detalle del ombligo y de las primeras cámaras. Se observa la concha embrionaria inicial tipo lapa, la constricción que marca el inicio de la pared ventral y el cambio de curvatura en la pared dorsal.
(Procedente de la imagen 3D de la Universidad de Dundee).
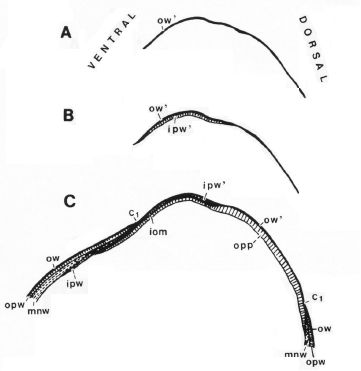
Así pues, el perfil de la concha embrionaria preseptal del Nautilus (Fig. 6) puede simplificarse o sintetizarse en dos líneas curvas: la que delimita la parte dorsal y la correspondiente a la ventral (parte izquierda y derecha respectivamente en la figura 6.B). Esta simplificación nos recuerda y hace pensar en la conjunción, antes señalada, entre la espiral longitudinal y la transversal observada en el análisis resumen expuesto en la introducción. Y esa perspectiva se refleja claramente en la sección de dicha concha embrionaria correspondiente a esa fase preseptal (Fig. 11) donde la parte dorsal embrionaria bien podremos catalogarla como el septo cero o inicial (Mutvei & Doguzhaeva, 1997, indican que el protosepto o capa interior sobre la concha inicial es un septo que carece de tubo sifuncular).
Precisamente es en la constricción de la cicatriz (C1 en la Fig. 11) donde la concha adopta la curvatura cordobesa en la pared ventral e inicia el cambio de concavidad en la pared dorsal, iniciándose el labio dorsal. Las figuras 12 a 14 muestran el desarrollo durante la formación de los tres primeros septos.
 |
 |
|
Fig. 11. Desarrollo sucesivo de diferentes capas inorgánicas en la concha preseptal del Nautilus. |
Fig. 12. Sección media dorsoventral de la concha embriónica del Nautilus macromphalus en la etapa del primer septo (S1) y engarce del sifúnculo (Procedente de Tanabe, and Uchiyama, 1997). |
 |
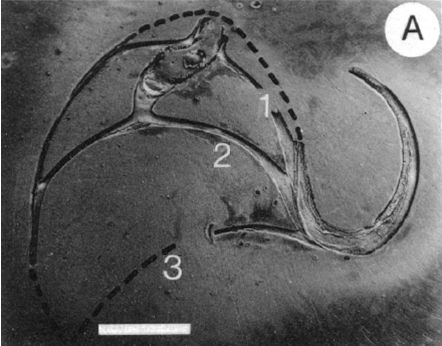 |
| Fig. 13. Sección media dorsoventral de la concha embriónica del Nautilus belauensis en la fase de dos cámaras (Procedente de Landmam et al.1989. Se corresponde con el ejemplar de la Fig. 9). | Fig. 14. Sección en la concha del Nautilus belauensis en la fase de tres cámaras. Las líneas discontinuas señalan las partes fragmentadas y perdidas al efectuar el corte. (Procedente de Landmam et al.1989). |
En la discusión que realizan en su artículo, Landman et al. (1989) exponen que la concha del Nautilus sufre marcados cambios durante la embriogénesis, en particular indican que durante la etapa de dos y tres cámaras, en el fragmacono, las proporciones que acontecen entre el volumen de las cámaras septales y el de la cámara habitacional son pequeñas y difieren de las alcanzados en etapas ontogénicas posteriores, ello es debido a que la longitud de la cámara habitacional es mucho mayor en la primera etapa vital que en la fase juvenil y adulta. Sin embargo, el perfil de la concha sí se asemeja en todas las fases.
Con la base y los detalles aportados hasta ahora, nos surge el interrogante acerca de: ¿qué acontece con nuestro modelo cordobés uniforme (con igual forma durante todas las etapas vitales) del Nautilus —un modelo bien adaptado a nivel global y macroscópico, como ya hemos mostrado en detalle— si lo confrontamos con esa fase inicial, que biológicamente está indicada como diferenciada? Pues, de partida, lo que ocurre es que se inicia una nueva etapa investigadora, un nuevo camino que recorrer a hombros de estos gigantes biológos, antes explícitamente citados, y de otros muchos más omitidos por economia literaria, pero por supuesto no olvidados, y junto a los de numerosos gigantes matemáticos poder modestamente contribuir a la "Ontogenia matemática del Nautilus". ¡Avancemos, pues!
Para poder adentrarnos en este análisis y contraste, podemos aglutinar todo lo indicado en un recurso interactivo ( ver la escena interactiva 1) que nos permita tener una visión solapada comparativa y que ayude en la conceptualización de lo que acontece, es decir, partir de una agrupación de instantáneas para lograr extraer un continuo descriptivo matemático. Es obvio, de nuevo es necesario indicarlo aunque pueda ser reiterativo, que la superposición de las fotos anteriores mostrará variaciones, algunas debido a que proceden de diferentes ejemplares y especies de Nautilus, otras serán consecuencia de la variabilidad que intrínsecamente acontece en todo espécimen o individuo concreto dentro de las características comunes e identificadoras que comparten y que definen a esa especie; o quizás que estén generadas por posibles desviaciones angulares al realizar los cortes sobre la concha para obtener su sección o perfil. En definitiva, errores comunes e implícitos en cualquier estudio y que aquí, adicionalmente, se ven magnificados gracias a la amplificación visual que nos aporta la técnica. Pero en esa escena, si alguien tiene un empeño cuantificador especial, puede verificar ―con la regla interactiva que se dispone― que nos adentramos en variaciones en el entorno de la décima de milímetro. Estos son detalles con los que se ha de convivir y que han de ponderarse en su justa magnitud para lograr esa visión global y poder encuadrarse en la perspectiva de búsqueda de un modelo o patrón conceptual y así lograr encontrarlo.
A continuación puede interactuar con dicho recurso interactivo y podrá abordar, si lo desea, su investigación personal a través de las diferentes herramientas que ahí se incluyen:
Escena interactiva 1. El modelo cordobes uniforme del Nautilus (revisión)
Nuestra reflexión la dejamos reflejada en la siguiente presentación y puede también usarse como guía a reproducir en la escena interactiva anterior.
Así pues, el análisis realizado nos marca varias necesidades:
- Necesidad de modelar el labio dorsal y el ombligo.
- Necesidad de estudio específico de la concha del Nautilus en el primer verticilo y su ontogenia en general.
- Necesidad de mejorar el modelo de confluencia de septos y paredes en el segundo y tercer verticilo.
En definitiva, contemplamos y concluimos que es obvia la necesidad de abordar la citada "Ontogenia matemática del Nautilus"... Y a ello nos dedicaremos en el siguiente artículo. Para no impacientarse "juegue" con el recurso interactivo aportado y adéntrese en los artículos indicados en la bibliografía descrita.
Bibliografía
MolluscaBase eds. (2021). MolluscaBase. Patella vulgata Linnaeus, 1758. Accessed through: World Register of Marine Species at: http://www.marinespecies.org/aphia.php?p=taxdetails&id=140685 on 2021-08-22
Landman, N. H., Arnold, J. M. and Mutvei, H. 1989: Description of the embryonic shell of Nautilus belauensis. American Museum Novitates, no. 2960, p. 1–16.
Mutvei, H. and Doguzhaeva, L. 1997: Shell ultrastructure and ontogenetic growth in Nautilus pompilius L. (Mollusca: Cephalopoda). Palaeontographica Abteilung A Palaeozoologie–Stratigraphie, vol. 246, p. 33–52.
Sasaki, T., Shigeno S. & Tanabe K. 2010. Anatomy of living Nautilus: Reevaluation of primitiveness and comparison with Coleoidea (2010) in Tanabe, K., Shigeta, Y., Sasaki, T. & Hirano, H. (eds.) 2010. Cephalopods - Present and Past, Tokai University Press, Tokyo, p. 35-66.
Saunders, W. B., and N. H. Landman (eds.) 2010. Nautilus: the biology and paleobiology of a living fossil. (Springer. First edition New Y 1987) Plenum Press, New York.
Tanabe K. & Uchiyama, K. 1997. Development of the Embryonic Shell Structure in Nautilus. The Veliger 40(3): 203-215.

Este obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Hace unos años mostramos que la forma y el crecimiento del Nautilus, prototipo de belleza natural y matemática, era neta y completamente cordobés. No obstante, manteniéndose dentro de ese canon, el desarrollo no es uniforme en todas sus etapas vitales y, en particular, en su etapa inicial marca diferencias que son dignas de modelar. Así pues, nos planteamos trasladarles en varios artículos de este blog la ontogenia matemática del Nautilus y le mostraremos que en la primera etapa el modelo se corresponde con un patrón de dos espirales cordobesas con diferente polo y, sin embargo, en la etapa juvenil y adulta éstas comparten el mismo polo. Un mínimo detalle que hay que añadir al buen hacer matemático de este animalito y que da explicación a su acontecer vital, permiténdonos comprender nuevos detalles de su ser.
Quedan invitados a su lectura y quedamos deseosos de sus comentarios y observaciones
Introducción
El Nautilus, usualmente catalogado como un fósil viviente ―si bien Ward (1984) lo encuadra en una estasis aparente[1]―, ha llamado siempre la atención no sólo por la belleza exterior de su concha, quizás no excesivamente destacable frente a la de otros moluscos, sino por aquella que esconde en su interior, ¡que es sorprendente!, y no deja indiferente a nadie. Por ello, ha sido ampliamente estudiada desde el punto de vista paleontológico, zoológico, biológico u ontogénico, pero también en el mundo artístico, el arquitectónico, el ingenieril, el físico-químico y, por supuesto, en el matemático. Incluso ha llegado a ser idealizada en estos entornos científicos, sin olvidar el contexto literario donde también se ha adentrado en lugares preminentes. Aupada como prototipo de belleza ha sido continuamente encajonada de manera forzada en el canon de belleza o proporcionalidad divina o áurea, a pesar de su resistencia y continuo grito de: ¡No!, ¡No soy áureo!, clamor que puede ser inaudible para legos, pero no debería serlo para eruditos. Más fácil hubiera sido haber creado la proporción nautílica, como referente o neotipo de belleza, que con rocambolescas maneras tratar de estirar, contraer o moldear su fina superficie calcárea, pues ello es una suerte imposible de lograr con tan frágil soporte.
En el artículo “Sobre la forma y el crecimiento cordobés del Nautilus pompilius” (Galo, Cabezudo y Fernández, 2016 a) detectamos y expusimos que la espiral logarítmica que se ajusta al perfil de la concha del Nautilus se corresponde con una espiral cordobesa (Fig. 1).

Fig. 1. Ajuste del Nautilus por una espiral logarítmica cordobesa (Galo et al. 2016 b).
Este hallazgo coyuntural que no deja de ser una mera coincidencia numérica, aunque para nosotros muy agradable, con la razón denominada cordobesa y que consecuentemente nos permite asociar su nombre al de Nautilus, hubiera quedado como una curiosidad anecdótica si no fuera porque ahí señalamos y detallamos (ver Fig. 2 y 3) que todo en el Nautilus se muestra cordobés ―sí, nosotros estuvimos silenciosos y atentos y le oímos decir: ¡Qué soy cordobé![2] (ver Fig. 4) ―:
- El rastro calcáreo del sifúnculo (órgano que vacía las cámaras y actúa en la consecución de la flotabilidad del animal) muestra que éste crece siguiendo la forma de esa espiral cordobesa y que es el eje de simetría del teórico cono topológico que forma la cavidad que ha ido construyendo y recorriendo el animal en su ciclo vital.
- Los septos (tabiques que conforman las cavidades de flotación) son arcos de una espiral que es también cordobesa.
- El polo de esos arcos septales se desplaza siguiendo una espiral del mismo tipo, cordobesa, que es la mediatriz de todos los radios vectores de la espiral de la concha.
- Todo punto de la concha o interior es la intersección de dos espirales cordobesas, una longitudinal (tipo a la del perfil de la concha, pero con un factor de escala) y otra transversal (tipo septal).
 |
 |
|
Fig. 2. Espiral que aproxima perfil de la concha (azul), la de los septos (amarilla) y la que describe el polo de los arcos septales (magenta). |
Fig. 3. Detalle de la espirales sobre las que se aproximan los septos: perfil de la concha (azul ),septos (amarilla) y la que describe el polo de los septos (magenta). |
 |
|
Fig. 4. El Nautilus es “cordobé”. |
Así pues, en el artículo citado ” (Galo, Cabezudo y Fernández, 2016 a) se buscó y se logró captar la esencia nautílica matemática a nivel conceptual global: “todo en el Nautilus se muestra cordobés”, y el modelo matemático que ahí se consideró fue único e indiferenciado en todo el crecimiento. Se aplicó la consideración de que dado que el crecimiento del Nautilus es gnomónico, es decir, que mantiene su forma cambiando su escala, se puede hacer una lectura atemporal esperando que el modelo sea aplicable en toda la fase vital desde su germen a su madurez. No obstante, esto, no es más que un útil deseo purista matemático que se mostrará débil para cualquier detenido observador que aborde su confrontación con la realidad, pues somos conscientes por experiencia vital personal que en el desarrollo de un ser vivo acontecen diferentes fases o etapas que introducen matices distintivos dentro de una esencia identificadora que permanece. Y siguiendo esta línea diversificadora, en este artículo lo que se persigue es abordar la ontogenia matemática del Nautilus, desde su periodo embrionario hasta la madurez y determinar cuál es el modelo matemático diferenciado en cada una de las etapas de crecimiento en correlación con los estudios biológicos micro y macroscópicos existentes. Y, de hecho, aquí veremos que se pueden diferenciar tres etapas que esencialmente se corresponden con cada uno de los tres verticilos (un verticilo es una revolución de 360° en el crecimiento en espiral de la concha de un molusco) que se contabilizan en la espiral de la concha de un ejemplar adulto, tres etapas que encierran ciertas diferencias y matices dentro del citado modelo cordobés global. Todo, sin olvidar y teniendo siempre presente, siendo conscientes, que cuando atravesamos el canal que enlaza la discreta yocto-yotta realidad, en la que vivimos, con la idealizada continuidad del mundo matemático siempre surgen interferencias (“aliasing”) que trataremos de mitigar y/o detallar, aunque hay que asumirlas.
La referencia zoológica de la que partiremos es: “Anatomy of living Nautilus: Reevaluation of primitiveness and comparison with Coleoidea” de Sasaki, Shigeno & Tanabe (2010) donde, aportando unas magníficas fotografías, se aborda una revisión de la anatomía del Nautilus, que si bien se centra principalmente en los órganos y partes blandas, incluye también información sobre la forma embrionaria de la concha. Adicionalmente, en la introducción de ese artículo los autores detallan la literatura más significativa al respecto comenzando con el libro de Saunders and Landman (1987) que compila el conocimiento sobre el Nautilus hasta ese año y que posteriormente ha sido actualizado en la edición de 2010. Ladman et al. (1989) analizan la concha en el periodo embrionario y muestran su desarrollo hasta el tercer septo, estudio que se complementa en Mutvei and Doguzhaeva (1997), donde se muestran las curiosas depresiones dorsales septales en el segundo verticilo, y en Tanabe and Uchiyama (1997). Estos artículos nos servirán de soporte, guía y verificación en nuestro análisis matemático. También el modelo virtual tridimensional e interactivo de la concha del Nautilus del “D’Arcy Thompson Zoology Museum”, obtenido mediante escáner, es una magnífica fuente de observación visual interactiva, si bien hay que tener presente y es ostensible que el corte del ejemplar que se ha usado para su digitalización no coincide con el plano medio de simetría. Pueden consultarse otros modelos tridimensionales en Sketchfab.
| Modelo tridimensional de la sección de la concha de un Nautilus pompilius. |  |
|
Nautilus Shell (sectioned) by University of Dundee Museum Collections on Sketchfab |
Cortes por planos paralelos al plano medio obtenidos por González-Restrepo (2019) a partir del modelo 3D del Museo Dundee. |
La concha embrionaria y el primer verticilo
Landman et al. (1989) exponen que la forma de la concha del Nautilus sufre marcados cambios durante la embriogénesis y que los perfiles en la etapa de dos y tres cámaras difieren de los alcanzados en etapas ontogénicas posteriores. En nuestro artículo (Galo et al., 2016 a) ya pusimos de manifiesto (Fig. 5) que en el primer verticilo se contabilizaban ocho cámaras, frente a las dieciséis del segundo, es decir, cambia el paso interseptal teórico que en un primer momento es π/4 y posteriormente pasa a ser π/8. Este paso se mantiene también en el tercer verticilo, si bien en esta fase adulta pueden acontecer ciertos cambios morfológicos que influyen en los últimos septos y ése paso puede ser algo menor. En la imagen de la fig. 5 son ocho los septos en el tercer verticilo, pero este número es variable. A pesar de indicar estas diferencias, allí, optamos por presentar un modelo matemático teórico uniforme considerando un crecimiento idéntico en toda la vida del animal y ello permitió fijar los comportamientos globales antes citados como que el sifúnculo sigue el eje de simetría topológico de la cámara habitacional o que los polos de los septos se ubican en la espiral mediana, propiedades que ahora, en un proceso inverso, nos serán de utilidad para analizar y comprender lo que acontece en ese diferenciado primer verticilo. Y ese estudio es el que abordaremos en esta sección donde nos detendremos en la fase embrionaria precameral, en la fase de formación de las primeras cámaras y en lo que acontece en el resto de este primer verticilo.
 |
|
Fig. 5. Recuento de verticilos y cámaras en el Nautilus. |
En el análisis de ese primer verticilo nos adentraremos en un próximo artículo de este blog... no tardará en llegar.
[1] “Rather than being a prime example of a living fossil, the nautiloids may be examples of rapidly speciating organisms that change only slightly during each event, and return to the same form over and over. The result would be apparent stasis, but the actual history would be similar to that of any other rapidly speciating group-except that the net morphologic change over time would be small, rather than large” (Ward, 1984).
[2] En Córdoba (España) la pronunciación de las eses a final de palabra suele ser muy débil y para los oídos no habituados a esa tonalidad, éstas quedan como omitidas.
Bibliografía
Galo J.R., Cabezudo A. y Fernández I.(2016 a) : Sobre la forma y crecimiento cordobés del Nautilus Pompilius. Epsilon, 2016, Vol. 33 (3), nº 94.
Galo J.R., Cabezudo A. y Fernández I.(2016 b) : Recurso interactivo Sobre el crecimiento cordobés del Nautilus Pompilius. Red Educativa Digital Descartes.
González-Restrepo, F. (2019): Cortes del Nautilus a partir de la digitalización 3D del museo Dundee. Red Descartes Colombia.
Landman, N. H., Arnold, J. M. and Mutvei, H. 1989: Description of the embryonic shell of Nautilus belauensis. American Museum Novitates, no. 2960, p. 1–16.
Mutvei, H. and Doguzhaeva, L. 1997: Shell ultrastructure and ontogenetic growth in Nautilus pompilius L. (Mollusca: Cephalopoda). Palaeontographica Abteilung A Palaeozoologie–Stratigraphie, vol. 246, p. 33–52.
Sasaki, T., Shigeno S. & Tanabe K. 2010. Anatomy of living Nautilus: Reevaluation of primitiveness and comparison with Coleoidea (2010) in Tanabe, K., Shigeta, Y., Sasaki, T. & Hirano, H. (eds.) 2010. Cephalopods - Present and Past, Tokai University Press, Tokyo, p. 35-66.
Saunders, W. B., and N. H. Landman (eds.) 2010. Nautilus: the biology and paleobiology of a living fossil. (Springer. First edition New Y 1987) Plenum Press, New York.
Tanabe K. & Uchiyama, K. 1997. Development of the Embryonic Shell Structure in Nautilus. The Veliger 40(3): 203-215.
Ward P. (1984) Is Nautilus a Living Fossil?. In: Eldredge N., Stanley S.M. (eds) Living Fossils. Casebooks in Earth Sciences. Springer, New York, NY. https://doi.org/10.1007/978-1-4613-8271-3_31

Este obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Primer número de la "Revista Digital RED Descartes"
Escrito por José R. Galo SánchezEn este mes de agosto de 2021 hemos publicado el primer número de nuestra nueva publicación periódica: "Revista Digital de la RED Descartes", panhispánica, educativa e interactiva. La periodicidad inicial prevista es semestral y acoge artículos en español, inglés y portugués con un contenido ligado a los fines de nuestra ong RED Descartes, pero abierta a entornos análogos o similares.
Abrimos una nueva línea de trabajo, inmersa en nuestro sello editorial y servicio altruista, con vocación de seguir transmitiéndoles interés por la educación y, en particular, con la utilización de los recursos educativos interactivos de nuestro proyecto Descartes, desarrollados con la herramienta homónima: Descartes y en una revista con soporte en los “Libros interactivos de RED Descartes”. Confiamos poder rebatir a Quintiliano cuando afirmaba: “Facilius est multa facere quam diu” ―Es más fácil hacer muchas cosas que hacer una durante mucho tiempo―, pues en la trayectoria de nuestro proyecto ya hemos demostrado que desde Descartes se ha hecho mucho por la educación durante mucho tiempo (desde 1998) y que la apertura de nuevas tareas no son más que facetas poliédricas de un único y sólido proyecto. Confiamos en poder seguir haciendo lo mismo, durante mucho tiempo más.
La “Revista Digital Red Descartes” tiene como objetivo principal la difusión de todo lo concerniente al proyecto Descartes ―proyecto educativo de ámbito global que persigue la mejora de la educación apoyándose en las tecnologías de la información y de la comunicación (TIC) y en las del aprendizaje y el conocimiento (TAC)―, pero con visión abierta a acoger todo aquello que signifique un avance significativo en el ámbito educativo con herramientas y recursos similares.
| Para acceder al primer número pulse sobre la imagen |
Ciertamente, puede indicarse que desde nuestro servidor de contenidos proyectodescartes.org se genera esa difusión por sí sola y que en él, concretamente en el blog, periódicamente se publican artículos que desarrollan diferentes contenidos y casuísticas técnicas, educativas, participativas, difusoras de actividades, etc,. que pudieran considerarse como suficientes para cubrir ese objetivo; no obstante, la revista busca sistematizar esa divulgación aglutinándola en un soporte organizativo más tradicional como es el de publicaciones periódicas en fascículos o números, que van constituyendo volúmenes anuales y estos, a su vez, generan una colección temática identificadora. Esta agrupación de artículos y ese encadenamiento fasciculado aporta cierto reposo y perdurabilidad, al menos sensorialmente, frente a la volatilidad que transmiten las publicaciones en línea tipo blog, lo cual no es óbice, aunque parezca paradójico, para que esta revista sea una publicación que nace con una distribución digital exclusivamente en línea.
Nuestra revista se caracteriza y distingue por ser una publicación interactiva, es decir, aporta como elemento identificador el que dentro de su contenido aparecen elementos que dan respuesta adecuada, contextualizada, a las acciones que sobre ellos realice el lector/actor. Esa interactividad es identificadora del aporte que suministran los recursos desarrollados con nuestra herramienta Descartes, pero sin exclusividad a ellos. Nuestra línea de trabajo está abierta a cualquier recurso promotor del aprendizaje y del conocimiento, aunque tengamos obviamente nuestra predilección personal básica por lo que promovemos, desarrollamos y difundimos ¡desde casi un cuarto de siglo de existencia!
Y, como no podría ser de otra forma, para dar formato a la revista utilizaremos otra herramienta propia ―de desarrollo propio, pero de uso libre―, los “Libros interactivos de la RED Descartes”. Un soporte técnico informático que facilita la composición y el formato editorial, permitiendo la inclusión de cualquier objeto multimedia e interactivo sin más limitación que su compatibilidad con el estándar HTML5.
¡Quedáis invitados a publicar vuestros artículos en nuestra revista! Como referencia para la composición de su contenido podéis consultar las "Normas de publicación" y para cualquier duda o propuesta quedamos atentos en nuestra dirección de correo Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo..
Más...
Educación abierta: Curso "Edición de libros interactivos" de la RED Descartes
Escrito por José R. Galo Sánchez
Como se hizo. Envío de datos a un juego desde un iframe html embebido en él
Escrito por Jesús Manuel Muñoz CalleLos juegos del Proyecto AJDA y las escenas de DescartesJS en general, pueden contener páginas HTML integradas en ellos, de forma que un espacio del juego sea una página HTML. Vamos a analizar como se envían datos al juego desde el iframe HTML que está embebido en él,lo cual tiene diversas utilidades que trataremos en otros artículos
El iframe que está embebido será una sencilla página HTML, que llamaremos hijo.html y que contiene en su cuerpo dos elementos de entrada de datos, un campo de texto (con identificador CT) y un selector (con identificador SL):
<input name="textfield" type="text" id="CT" value="Campo de texto" >
<select name="selec" id="SL">
<option value="0" selected></option>
<option value="1">A</option>
<option value="2">B</option>
<option value="3">C</option>
<option value="4">D</option>
</select>
Para que se puedan enviar los datos al juego, en la cabecera del iframe embebido en el juego se debe incluir el siguiente código:
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)













 CONTACTO
CONTACTO
