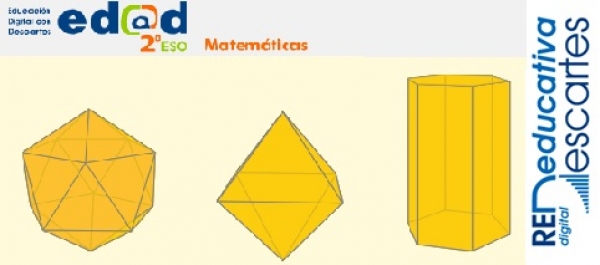
Esta semana presentamos varias actividades de autoevaluación propuestas en la unidad de geometría cuerpos geométricos de 2º ESO de Ed@d.
Cada una de las actividades contiene una serie de preguntas tipo test sobre diferentes conceptos: poliedros, prismas, pirámides y cuerpos redondos. En cada actividad se proponen 15 preguntas con tres opciones para cada una de ellas. Al final se obtiene una nota a partir de los aciertos y errores.
Para su aplicación en el aula se propone crear un enlace a cada una de las actividades en un curso Moodle. En el siguiente vídeo se muestra todo el proceso.
EDAD 4º ESO Aplicadas - Semejanza y trigonometría
Escrito por Alfonso Saura EspínEste mes hemos tratado la unidad de Semejanza y trigonometría
y hemos tratado los siguientes epígrafes:
1.Semejanza
Teorema de Tales
Triángulos Semejantes
Teorema de Pitágoras
Cálculo de distancias
2.Razones trigonométricas
Definición
Relaciones fundamentales
3.Resolución de triángulos rectángulos
Dos lados
Un cateto y un ángulo agudo
Hipotenusa y un ángulo agudo
La Probabilidad Total. Ejercicios.
Escrito por Ildefonso Fernández TrujilloMisceláneas. La probabilidad total.
A las cuentas del estado tradicionalmente se les ha llamado estadísticas y habitualmente estas cuentas se han dado a conocer por parte de los sucesivos gobiernos de forma periódica. En la actualidad el diccionario define la estadística como: Ciencia que utiliza conjuntos de datos numéricos para obtener, a partir de ellos, inferencias basadas en el cálculo de probabilidades. En la wikipedia encontramos: "La estadística (la forma femenina del término alemán Statistik, derivado a su vez del italiano statista, "hombre de Estado") es una rama de las matemáticas y una herramienta que estudia usos y análisis provenientes de una muestra representativa de datos, que busca explicar las correlaciones y dependencias de un fenómeno físico o natural, de ocurrencia en forma aleatoria o condicional...."
Dentro de la particularidad que nos ocupa: la probabilidad total, también hemos de tener en cuenta el juego ya que diferentes artistas y científicos interesados en el azar lo han tomado como referencia para elaborar obras y contenidos de indudable valor. En este sentido mostramos a continuación la imagen de una ruleta donde se recomienda el estudio de la situación de los números en la misma.
La imagen anterior enlaza con uno de los blogs del escritor, bloguero y divulgador "freelance" (por libre) Alfred López sobre curiosidades generales, donde muestra una breve pero selecta información relacionada con el tema de la probabilidad y la ruleta. (En este enlace se expone la procedencia de las imágenes que se usan)
En la imagen siguiente puede verse el mantel (que incorpora el cero) de la mesa de juego de la ruleta, lo que nos permite seguir la exposición enlazada anteriormente.
En la Wikipedia podemos documentarnos, de manera concisa y precisa, sobre el azar
Enlazamos, a continuación con el esmerado trabajo JUGANDO CON LA PROBABILIDAD, elaborado por un grupo de profesores de la Universidad de Granada.
Lo dicho anteriormente y la propia experiencia nos lleva al objetivo principal de esta entrada, un intento de análisis del alma del azar, la incertidumbre. Cuando, a relativamente temprana edad, nos enfrentamos formalmente con la resolución de situaciones donde interviene el azar, ya llevamos un bagaje de conocimientos adquiridos naturalmente a través de los juegos en familia o con las amistades, es decir, ya conocemos la incertidumbre. Pero este conocimiento, lejos de ayudar, en principio parece ser perjudicial, ya que automáticamente la intuición prevé que la solución de una situación donde interviene el azar es inútil ya que fácticamente y de forma inmediata no tiene ningún sentido tangible, es imposible de constatar fácticamente. Más adelante cuando aceptamos la utilidad del conocimiento de la tendencia de un suceso y es más, cuando la realidad nos muestra como una probabilidad se convierte en un hecho fáctico previsto gracias a un buen estudio previo basado en el azar es cuando percibimos la importancia fundamental del conocimiento de las herramientas estadísticas y su utilización. Como introducción a ese estudio y suponiendo que la persona que accede a este artículo ya posee una base elemental de los fundamentos estadísticos y de probabilidad, hemos elaborado la siguiente utilidad donde se analizan y resuelven situaciones relacionadas con la probabilidad total de un suceso.
En esta ocasión, en la sección de vídeo, hemos elegido uno que muestra, en francés, la introducción al teorema de Bayes.
Animamos a colaborar elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo. 2018
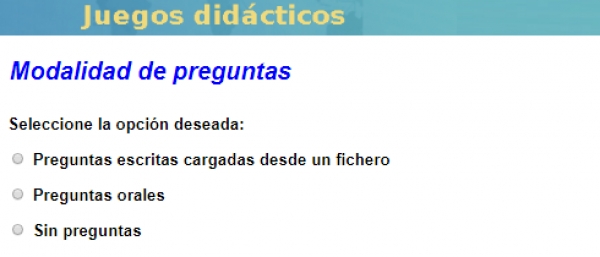
Modalidades de introducción de preguntas en los juegos del Proyecto AJDA
Escrito por Jesús Manuel Muñoz Calle- Preguntas escritas cargadas desde un fichero. El fichero de preguntas se carga antes de iniciar la partida.
- Preguntas orales. El presentador del juego formula las preguntas y verifica las respuestas.
- Sin preguntas. Modalidad en la que no se formulan preguntas con contenidos específicos.
- Preguntas escritas cargadas a mano al principio del juego. Antes de empezar la partida se escriben las preguntas y respuestas en el propio juego en un formulario destinado a tal fin. Estos contenidos se pierden al finalizar la partida.
- Preguntas escritas generadas por juego con verificación de respuesta. El juego dispone de contenidos cargados y verifica las respuestas a los mismos.
Dependiendo de la modalidad elegida, las preguntas se realizarán de una forma u otra. Por ello, es importante que el presentador disponga de los recursos necesarios dependiendo de la modalidad elegida, es decir, si se va a utilizar un fichero se deberá tener éste preparado, si se van a hacer las preguntas orales, estar preparado para realizarlas y corregirlas o si se van a introducir las preguntas al principio del juego realizarlo antes de comenzar el juego.
Más...
¿Conoces lo que es la simetría axial? @prende.mx
Escrito por Montserrat Gelis BoschEsta semana presentamos la unidad interactiva Simetría, un recurso educativo para la introducción de este concepto en los últimos cursos de primaria.
Este objeto digital pertenece al subproyecto aprende.mx de la RED. Las unidades de este subproyecto han sido desarrolladas con la herramienta DescartesJS y se han realizado en colaboración con el gobierno mejicano para su proyecto aprende.mx.
El proyecto aprende.mx es una iniciativa de la Secretaría de Educación Pública del gobierno mejicano. Consta de aplicaciones, recursos educativos y programas digitales para los últimos cursos de primaria. Algunas de estas actividades han sido desarrolladas con la herramienta DescartesJS, y se divulgan desde la Red Educativa Digital Descartes dentro del subproyecto aprende.mx.
Los materiales están clasificados en tres bloques: matemáticas, ciencias y castellano. En el bloque de matemáticas encontramos actividades sobre distintos contenidos: números, medida, geometría, estadística y probabilidad.
En este vídeo se muestran con detalle las actividades de la unidad simetría.
EDAD 3º ESO Académicas - Movimientos en el plano
Escrito por Alfonso Saura EspínEste mes vamos a ver los movimientos en el plano, correspondientes a 3ºESO Académicas:
1.Vectores
Concepto de vector. Coordenadas
Vectores equipolentes
Suma de vectores
2.Traslaciones
Traslación según un vector
Composición de traslaciones
3.Giros
Giro de centro O y ángulo α
Simetría central
Figuras invariantes de orden n
4.Simetría axial
Simetría de eje e
Figuras con eje de simetría
Composición de simetrías axiales
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)











 CONTACTO
CONTACTO
