EDAD 2º ESO Potencias y raíces de enteros
Escrito por Alfonso Saura EspínEste mes vamos a ver la unidad correspondiente a Potencias y raíces de enteros. Esta unidad es muy corta porque es un repaso de los visto en 1º de la ESO:
Como hemos dicho es muy corta porque repasa los conceptos del curso anterior:
1.Potencias de un número entero
¿Qué es una potencia?
Signo de una potencia
2.Operaciones con potencias
Potencia de productos y cocientes
Producto y cociente de potencias
Potencia de una potencia
3.Potencias de base 10. Notación científica
Potencias de base 10
Notación científica
4.Cuadrados perfectos. Raíces cuadradas
Cuadrados perfectos
Raíces cuadradas
Descartes en la Universidad. Miscelánea: Extremos de funciones de dos variables. Método del Hessiano
Escrito por Elena Álvarez SáizAcceso a la miscelánea: Extremos de funciones de dos variables. Método del Hessiano.
En esta escena se muestra cómo realizar el estudio de los extremos relativos de una función diferenciable de dos variables.
Introducida la expresión de una función diferenciable y de sus derivadas parciales primeras, se puede analizar en primer lugar, qué puntos tienen el plano tangente horizontal (condición necesaria para que un punto sea extremo). Posteriormente, el método del hessiano permitirá determinar cuáles de esos puntos son máximos o mínimos relativos.
Este método se justifica utlilizando el polinomio de Taylor de la función de grado 2 centrado en el punto en el que se está realizando el análisis.
El vídeo siguiente explica el funcionamiento de esta escena.
Acceso a la miscelánea: Extremos de funciones de dos variables. Método del Hessiano.
Giros: una unidad PISA en comunicación audiovisual
Escrito por José Antonio Salgueiro GonzálezPublicamos hoy el sexto artículo dedicado a compartir y difundir algunas propuestas didácticas para el desarrollo de la comunicación audiovisual en nuestro alumnado a través de las Matemáticas con Descartes, fomentando su creatividad e imaginación y las técnicas necesarias del lenguaje cinematográfico y audiovisual, a la vez que proporcionarles una formación básica que les permita, de forma autónoma, generar y producir sus propios contenidos audiovisuales. Así, el equipo de esta producción ha elegido un escenario completamente diferente a los anteriores, con público incluido.
Recordamos y enlazamos a las publicaciones relacionadas con este proyecto: Desarrollo de la comunicación audiovisual a través de las Matemáticas con Descartes, Comunicación audiovisual con iCartesiLibri,Resolución de problemas y comunicación audiovisual y mutimedia con Descartes, ¡Diviértete! aprendiendo con Descartes y El ángulo de depresión y la comunicación audiovisual con Descartes.
Esta producción audiovisual está inspirada en la página "Giros", una unidad liberada de PISA integrada en la sección Miscelánea del Proyecto Descartes.
Entrevista al personaje misterioso (VIII)
Escrito por Eva M. Perdiguero GarzoY para finalizar este año 2014 tenemos a nuestro personaje misterioso (VIII). Cerramos el año, aunque no los programas con nuestros personajes históricos que cada día nos enseñan más y más. En esta ocasión, nuestro personaje nos acompaña desde la antigua Italia. Aunque como descubriremos en la entrevista nuestro personaje viajó por muchas ciudades comerciando y aprendiendo de todas las culturas. Pero no sólo aprendió sino que quiso enseñar a los demás todos sus descubrimientos, escribiendo un libro que poco a poco se fue extendiendo por todo occidente.
Escucha atentamente el podcast que puedes ver más abajo y dejanos tu comentario sobre quién crees que es este misterioso personaje. La semana que viene publicaremos su identidad a través de un puzle.
En la interpretación de nuestro personaje misterioso tenemos a nuestro compañero: José Mª Sorando, al que todos conocéis por su estupenda página web "Matemáticas en tu mundo"
El guión es obra de Eva M Perdiguero profesora de matemáticas y socia colaboradora de Red Educativa Digital Descartes. El trabajo lleva licencia CC BY-NC-SA 4.0. La entrevistadora y realizadora del podcast, también es Eva M Perdiguero.
Tanto los efectos especiales como la imagen del comienzo del artículo, pertenecen al Banco de sonidos del INTEF-MECD-ESPAÑA, tienen licencia CC BY-NC-SA 3.0 y han sido adaptados para esta ocasión.
Más...
En el artículo anterior se hicieron algunas reflexiones acerca de la creación de una pequeña utilidad didáctica, con el editor de escenas "Descartes", para uso en el aula. Como consecuencia se vio la necesidad de disponer de la librería que interpreta, en primera instancia, el código: el archivo 'descartes-min.js' y del editor de escenas, el archivo Descartes.jar.
También se comentó acerca de la conveniencia de organizar, de forma eficaz, la información, creando, en el directorio raíz, una carpeta con el nombre "Descartes", y en ella colocar los archivos Descartes.bat y Descartes.jar y, para el proyecto actual, añadir las carpetas: 'Europa', 'Asia', 'Africa', 'America' y 'Oceania'. En cada una de las cinco carpetas anteriores creamos las tres carpetas: 'css', 'imagenes' y 'lib', y dentro de esta última ponemos el archivo descartes-min.js.
La estructura tiene esta forma:
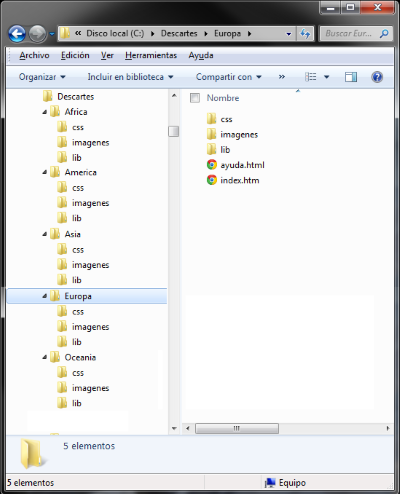
Otra de las ideas que se expusieron fué la de elaborar los esquemas gráficos y el guión de la escena. Esto es fundamental, y cuanto más precisos sean ambos: esquema y guión, más se nos facilitará la tarea de creación.
Por último necesitamos contar con todos los elementos auxiliares que van a intervenir en la escena, gráficos, sonidos, vídeos, enlaces, ficheros y demás. En el gráfico siguiente se observa parte del contenido de la carpeta imágenes para el apartado 'Europa' del proyecto. Muchas de estas imágenes se reutilizarán en los siguientes apartados: Asia, África...
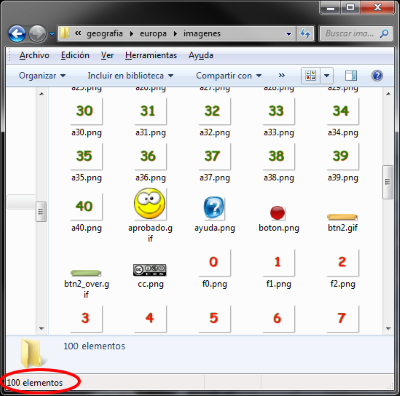
Si ya tenemos todos los actores, el guión con los esquemas y el archivo que hemos decidido usar como referencia (si es el caso; si no en lugar de en el menú del editor elegir: archivo > abrir, se elige: archivo > nuevo), es el momento de cargar la plantilla y comenzar a adaptarla a nuestro proyecto. En el vídeo siguiente se muestran los primeros pasos del proceso de adaptación del archivo que hemos elegido como referencia usando el editor de escenas "Descartes".
En siguientes artículos se explicará como desarrollar, terminar y probar la utilidad.
Recordamos que el resultado que se pretende conseguir es el que muestra la imagen-enlace siguiente.
Entrevista a Sixto Romero Sánchez. Presidente de la Sociedad Andaluza de Educación Matemática Thales.
Escrito por Ángel Cabezudo BuenoPor Ángel Cabezudo Bueno – 24 de noviembre de 2014
Sixto Romero Sánchez es profesor del Departamento de Matemáticas en la Escuela Técnica Superior de Ingeniería de la Universidad de Huelva,  con 39 años a su espalda como investigador y docente es catedrático en el área de Matemática aplicada.
con 39 años a su espalda como investigador y docente es catedrático en el área de Matemática aplicada.
Responsable en esta universidad del grupo de investigación “Modelización matemática, redes y multimedia”, actualmente trabaja en lo que se denomina Tratamiento Digital de Imágenes con importantes aplicaciones en Arqueología, Geología, Medicina, Biología, etc… y en la obtención de modelos para determinación y predicción de datos.
Desde hace años dedica su tiempo a la innovación docente aplicada a la mejora y enseñanza de las Matemáticas siendo en la actualidad Presidente de la Sociedad Andaluza de Educación Matemática Thales y Vicepresidente a nivel internacional de The Commission for the Study and Improvement of Mathematics Teaching (CIEAEM). Además preside la Academia Iberoamericana de La Rábida desde 2007, que se centra en el estudio de cualquier tema histórico, literario, artístico, científico o técnico, relacionado con la cultura y la sociedad andaluzas, así como en la interrelación entre éstas y la cultura y la sociedad iberoamericanas.
Desde aquí agradecemos a Sixto que entre tantos compromisos como tiene nos haya hecho un hueco y nos permita conocer a través de su palabra y con más detalle acerca de Sociedad Andaluza de Educación Matemática (SAEM) Thales.
Gracias en mi nombre y en el de todos los compañeros que formamos Red Educativa Digital Descartes.
La entrevista paso a paso:
- ¿Cómo nació la SAEM Thales y cuáles son sus fines societarios? 3:21
- ¿Quién puede pertenecer a SAEM Thales y qué pasos tiene que dar para ello? 6:16
- SAEM es un organismo de iniciativa privada que cuenta con sus propios recursos técnicos y humanos, no obstante, ¿cuenta también con recursos externos, fruto de la relación con otras instituciones y entidades, públicas o privadas, para llevar a cabo algunas de sus propuestas? Detállanos, en la medida de lo posible, este conjunto total de recursos. 7:30
- Sabemos que el ámbito en el que actúa SAEM Thales no es sólo el andaluz, también participa en un contexto nacional e internacional en los procesos de enseñanza y aprendizaje. Danos cuenta de algunas de estas participaciones. 9:45
- Una de las acciones de la SAEM Thales es la de divulgación y popularización de las matemáticas. ¿Cómo lo lleva a cabo y en este sentido, cual es la característica que le distingue de otros medios? y también, ¿Qué papel juega en todo esto el Centro de Documentación Thales? 12:25
- ¿Qué opinas de la RED Descartes, sobre sus acciones y recursos educativos y también de su herramienta de desarrollo Descartes? 15:10
- Desde la sociedad SAEM Thales se promueve GeoGebra ¿no cabría promover también otras herramientas, entre ellas Descartes? 16:43
- Muchos socios andaluces de RED Descartes son socios de SAEM Thales ¿Crees que sería conveniente establecer una colaboración entre ambas asociaciones? En caso afirmativo ¿cómo consideras que podría plasmarse esa colaboración? 17:50
- Como profesor universitario y dada tu amplia experiencia y conocimiento en el uso de las TIC ¿nos podrás decir cómo se están usando en las aulas de la Universidad? ¿No deberían también incluirse las TIC en las pruebas de acceso a la misma? 19:05
- Para terminar, ¿hay algo de interés que no hayamos recogido en esta entrevista y que a tu juicio conviene añadir o matizar mejor? 22:22

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)


 CONTACTO
CONTACTO
