Entrevista al personaje misterioso (II)
Escrito por Eva M. Perdiguero Garzo
Tras el éxito de la emisión de nuestro primer personaje misterioso (las visitas se van acercando a las 1.000) hoy tenemos a nuestro segundo personaje. En esta ocasión es una mujer matemática. Durante la entrevista el personaje dará datos sobre su vida, estos datos te deberían de servir para averiguar de quién se trata. Tienes toda una semana para averiguarlo y dejar un comentario en este blog. En la anterior entrevista no hubo muchos participantes que se animaran a dejar su conjetura acerca del personaje, ¿lo pusimos tan difícil? Espero que esta semana haya más animación. Publicaremos todos los comentarios recibidos pero sin el nombre que hayan indicado, así dejaremos al resto de participantes con la emoción hasta el final. ¿Te animas?
Tras la semana de reflexión el lunes 4 de agosto publicaremos la solución a través de un puzle que nos mostrará la imagen de este segundo personaje misterioso.
El entrevistador es el profesor Ángel Cabezudo Bueno y la profesora Eva M Perdiguero interpreta a la matemática inquieta e ilustre que viene del más allá. Ambos profesores son socios colaboradores de Red Educativa Digital Descartes y autores del guión que lleva licencia CC BY-NC-SA 4.0.
Los efectos de sonido pertenecen al Banco de imágenes y sonidos del INTEF-MECD-ESPAÑA, tienen licencia CC BY-NC-SA 3.0 y han sido adaptados para esta ocasión.
El montaje del audio se ha realizado con la aplicación Audacity 2.0.4 y ha corrido a cargo de Eva M Perdiguero.
Discurso. Ángulos en un reloj analógico.
Escrito por Ildefonso Fernández TrujilloDiscursos
Son parte del proyecto Descartes. Consisten en pequeñas utilidades interactivas cuyo objetivo es afianzar un concepto. Se presentan como una página web dinámica y su metodología consiste en plantear y resolver una situación con la intervención de quien visita la página, caso de tener interés. Una vez completado el ejemplo, la utilidad propone un ejercicio similar al de la introducción para ser resuelto, pero esta vez, sin ayuda alguna. La página puede reiniciarse tantas veces como se desee y en cada ocasión los ejemplos y los ejercicios, con gráficos y datos, serán diferentes porque hay 27 opciones distintas.
Podemos acceder al discurso haciendo clic en la siguiente imagen
En este vídeo puede observarse la manera de utilizar el discurso.
Y en este otro enlace puede descargarse el discurso para su uso fuera de línea.
Ildefonso Fernández Trujillo. Julio 2014
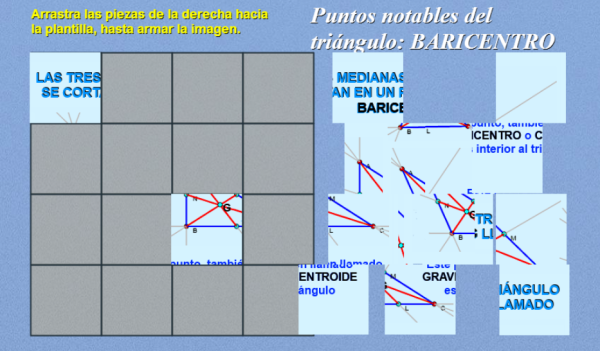
Puzles de puntos notables del triángulo: El Baricentro
Escrito por Ángel Cabezudo BuenoContinuamos en este artículo con la serie de puntos notables del triángulo tal como anunciábamos la semana anterior cuando presentábamos el Ortocentro. Hoy hemos elegido el Baricentro que también suele denominarse Gravicentro y Centroide según diferentes textos donde se consulte.
Se utiliza el puzle como recurso didáctico construido con DescartesJS. Cuando el puzle queda armado se observa una imagen de la posición que ocupa el baricentro en cada uno de los tres tipos de triángulo -rectángulo, acutángulo y obtusángulo- donde se dibujan las tres medianas, indicándose que en los tres casos el punto de corte, el baricentro, es interior. En este momento se repasa el concepto de mediana como recta y como segmento, se enumeran algunas propiedades que invitan a la reflexión y se proporcionan los enlaces a los materiales de consulta donde se puede dar respuesta a distintas cuestiones a través de la interacción con las escenas y las explicaciones más detalladas que allí se recogen.
La siguiente imagen lleva un enlace al puzle que se abrirá en una nueva ventana.
Una vez completada la publicación de la serie de puntos notables del triángulo, integraremos todos estos materiales en un único cuerpo didáctico que llevará por título “Puzles geométricos: Puntos notables del triángulo”.
Entrevista a Antonio de la Fuente Arjona. Autor del libro: La rebelión de los números.
Escrito por Eva M. Perdiguero Garzo
Antonio de la Fuente Arjona es un joven actor, autor de varios libros y director de teatro. Y es el autor de un libro llamado "La rebelión de los números". Un libro en el que se mezcla la aventura, el misterio y  (curiosamente) las matemáticas. El libro que está escrito en forma de obra de teatro, comienza la historia en un colegio cualquiera donde el profe de mates desaparece, en mitad de una de sus aburridas clases, y sus alumnos deciden ir al rescate. Los alumnos a pesar de no ser muy partidarios de las mates, pasarán por diversas pruebas que en circunstancias normales no habrían ni siquiera intentado,... ¿lograrán rescatar a su profe?
(curiosamente) las matemáticas. El libro que está escrito en forma de obra de teatro, comienza la historia en un colegio cualquiera donde el profe de mates desaparece, en mitad de una de sus aburridas clases, y sus alumnos deciden ir al rescate. Los alumnos a pesar de no ser muy partidarios de las mates, pasarán por diversas pruebas que en circunstancias normales no habrían ni siquiera intentado,... ¿lograrán rescatar a su profe?
Si quieres hacer teatro matemático con tus alumnos está es una buena opción. Los papeles se ajustan perfectamente a nuestros alumnos y puede llegar a ser muy divertido. El mismo autor nos habla sobre el teatro, una herramienta en la escuela en un artículo para la feria del libro.
Más...
Vacaciones con Descartes para las familias
Escrito por José Antonio Salgueiro GonzálezNuestros niños y niñas se encuentran disfrutando del período vacacional de verano, con mucho tiempo para compartir con sus familias y amigos, así como para el descanso y ocio. No obstante, siempre es recomendable encontrar el momento adecuado para sugerirles una interesante lectura y realizar, en nuestra compañía o junto a sus hermanos y hermanas mayores, algunas actividades de las áreas básicas del conocimiento. Ahora bien, para ello, las familias requieren de una orientación y asesoramiento que pueden recibir por diferentes canales de comunicación.
Con este fin, la Red Educativa Digital Descartes, ofrece una amplia selección de recursos digitales interactivos a los que pueden accederse desde cualquier lugar y hora, en el campo o en la playa, con un simple ordenador personal, portátil, tableta o smartphone y conexión a la red de internet, aunque también es posible descargarse el objeto de aprendizaje para usarlo en local, es decir, sin conexión a internet.
Estos recursos están organizados y catalogados por etapa educativa y edad, como se aprecia en la imagen inferior, así , las familias podrán seleccionar, con un simple clic sobre la imagen correspondiente o sobre el texto que la acompaña a su derecha, los adecuados para sus hijos e hijas, encontrando la relación con los nombres de las actividades y una breve descripción de la misma.
No obstante lo anterior, cada familia, como mejor conocedora de las capacidades de los niños y niñas, podrá optar por realizar las actividades de diferente edad.
La LOMCE no contempla los tres ciclos de Primaria, sino seis cursos independientes. lo que no supone obstáculo alguno para que los niños y niñas disfruten con estos recursos de gran calidad, pues accediendo al ciclo en cuestión, según la edad, y seleccionando el recurso deseado puede verse con detalle a qué curso concreto corresponde.
Esperamos que esta aportación, completamente gratuita, de la RED Descartes sea de utilidad para el mayor número posible de familias y animamos a dejar comentarios con sus opiniones.
El mapeado de la imagen se ha realizado desde la nube con la herramienta Image-Maps.
Proyecto Canals: inmersión digital de los materiales de Maria Antònia Canals
Escrito por José Antonio Salgueiro GonzálezEs el título de una de las comunicaciones presentadas por RED Descartes en el XV CEAM, Congreso de Enseñanza y Aprendizaje de las Matemáticas, organizado por la Sociedad Andaluza de Educación Matemática "Thales" y celebrado en la sede Antonio Machado de la Universidad Internacional de Andalucía en Baeza.
Parte de la labor educativa de María Antonia Canals ha quedado reflejada en el conjunto de materiales manipulativos que ha elaborado y compilado durante su extenso periodo docente. Desde el Proyecto Descartes se ha abordado la producción de recursos TIC que buscan contribuir a la difusión y conocimiento de esos materiales, pero introduciendo una perspectiva enmarcada en el uso educativo de dichas tecnologías y su funcionamiento en ordenadores, tabletas y smartphones gracias a la herramienta DescartesJS. Una inmersión digital que, si bien obliga a una reinterpretación, refleja y recoge la experiencia y guía educativa de la profesora Canals. Aquí se presentan 375 objetos de aprendizaje interactivos del Proyecto Canals: canales cartesianos hacia el conocimiento.
En primer lugar, compartimos el vídeo con el desarrollo y exposición, diapositiva a diapositiva, de la comunicación presentada. Pero, además, también ofrecemos una grabación realizada in situ con el smartphone, la presentación en formato HTML5, fruto del taller sobre "Presentadores de diapositivas HTML5", impartido exclusivamente para socios por Juan Guillermo Rivera Berrío, de la RED Descartes en Colombia, y finalmente el texto íntegro de la comunicación.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)







 CONTACTO
CONTACTO
